Temperature Effects of Electric Field on the First Excited State of Strong Coupling Polaron in a CsI Quantum Pseudodot∗
2018-01-22孙勇,丁朝华,肖景林
1 Introduction
With the development of low-dimensional nanoscale materials,such as quantum rod(QR),[1]quantum wire(QW)[2]and quantum dot(QD),[3]there has been a lot of theory and experiment work devoted to the understanding of energy states in low-dimensional semiconductor nanostructures.The physical properties of nanostructures such as phonon,electron and polaron characteristics will be more pronounced as the electron con finement effect increased with the reduction of dimensions.It is con firmed that many experimental works are vital for studying physical properties of low-dimensional semiconductor materials.For example,to achieve intersublevel population inversion,optical gain,and inter-sublevel polaron laser and optical pumping,Sauvage and Boucaud[4]proposed the three-level scheme based on n-doped InAs/GaAs self assembled quantum dots(QDs).By using photoluminescence excitation spectroscopy,Preisleret al.[5]firstly investigated the interband transitions(IT)in several ensembles of self-assembled InAs/GaAs QDs under strong magnetic field,and then determined the excitonic polaron energies.Finally they found the calculations were in good agreement with the experimental data which confirmed the existence of the excitonic polarons in the InAs/GaAs QDs. Due to electron-phonon(e-p)interactions(polarons),Xuet al.[6]experimentally studied the quantum dissipation and broadening mechanisms in self-formed In-GaN QDs.Many experimental works studied the polarons or e-p interactions in different(such as InAs/GaAs,InGN)QDs.It is the polaron that have the practical significance providing theoretical basis for the study of low dimensional quantum structures.
In the theories,there has been great interest in the phonon,electron and polaron properties of low dimensional structures(especially QD)using varies of methods. Jacaket al.[7]analyzed the aharmonicity induced relaxation of a polaron in GaAs/InAs QD by using Davydov diagonalization method.Hung[8]presented the theory of polaron resonance in QDs and self-assembled InGaAs/GaAs QD molecules.Verzelenet al.[9]reported on the polaron energies calculation in InAs QD molecules.In the above work they used different ways to study the phonon,the electron and the polaron in different kinds of QDs.However they did not consider the effects of different potentials on these variety of material QDs,needless to say in the strength-coupling RbCl material.
Recently,choosing the pseudoharmonic potential(PHP)that includes both harmonic and antidot potential,many investigators studied electron and polaron properties in different semiconductor materials.For example,Khordadet al.[10]obtained the e-p interaction influence on the third-harmonic generation in a GaAs QPD.In a two-dimensional GaAs QPD system,Liet al.[11]investigated polaron effects of the optical absorption coefficients and refractive index changes.Authors of our article[12]obtained the energy states in a strong-coupling electron-LO-phonon RbCl QPD and studied RbCl QPD qubit by employing the VMPT.However,the temperature effect on the energy states of the strong coupling polaron in the QPD has seldom studied by the researchers.Furthermore,base of the VMPT and QST,temperature effects of on the excited state of the strong coupling polaron in CsI QPD with electric field have not been studied yet.
In this research,we use the VMPT and QST to studythe temperature and strong-coupling polaron effects on the excited state energy in a CsI QPD.The investigated results have important theoretical significance,and are important for the implementation of the low-dimensional nanomaterial devices.
2 Theoretical Models
2.1 The First Excited State and Excitation Energy
An electron is confined in a RbCl QPD crystal with PHP and interacts with bulk LO phonons.In the presence of an external electric fieldF,the Hamiltonian of system is in the following form

where the physical quantities significances in Eq.(1)are the same with Ref.[13].

V(r)is the PHP[14]which includes both harmonic and antidot potentials.V0andr0are the two-dimensional electron gas(TDEG)chemical potential and the PHP zero point,respectively.
Employing the VMPT[15−17]and following the Ref.[18],the trial wavefunction is given by

where|φ〉depends only on the electron coordinate,|0ph〉is the phonon’s vacuum state withaq|0ph〉=0,andU|0ph〉denotes the coherent state of the phonon,fq(f∗q)is the variational function,we choose the trial polaron’s wavefunction of the ground and the first excited states(GFES)as Ref.[19]
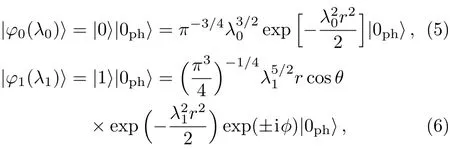
whereλ0andλ1are the variational parameters.By the VMPT,the polaron energy of the first excited state and the excitation energy in the CsI QPD can be described as
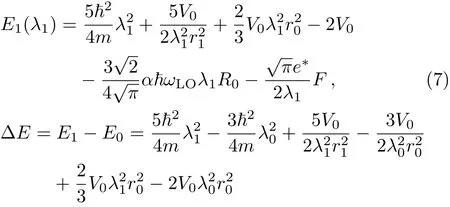

whereR0=(ħ/2mωLO)1/2plots the polaron radius.
2.2 The Transition Frequency and the Mean Number of LO Phonons
Based on the above investigated results,the transition frequency of the strong-coupling polaron in the CsI QPD is obtained as

The mean number of LO phonons around the electron can be described as

2.3 Temperature Effects
As the electron is at a finite temperature,the e-p system is no longer in the ground state completely.The lattice vibrations excite not only phonons but also electrons in the electric field and harmonic potential.The different states statistical average value of can be described the polaron properties.According to the QST,the optical phonons statistical average number is

whereKBandTare the Boltzmann constant and the system temperature,respectively. Through the selfconsistently calculation in Eq.(10)and Eq.(11),we can obtain the relation between variational parametersλ0,λ1and the temperatureT.From the above Eqs.(7)–(9),we find that the FESE,excitation energy and transition frequency of polaron depends on the variational parametersλ0,λ1and furthermore relates to the temperatureT.
3 Numerical Results and Discussions
Choosing CsI crystal,we illustrate the numerical results for the parameters appropriate to a QPD system and the parameters used in our calculations areme=9.1×10−31kg,m=0.42me,ħωLO=11.228 452 66 meV andα=3.67.[20]
In a QPD system and under electric field,the FESE,transition frequency and excitation energy of stronglycoupled polaron as a function of the temperature has been described in Figs.1–3 for four different electric fields,such asF=1.0,4.0,7.0 and 10.0 V/cm respectively. The TDEG chemical potentialV0is set to be 10.0 meV,the PHP at zero pointr0=12.0 nm and the polaron radiusR0=6.0 nm.
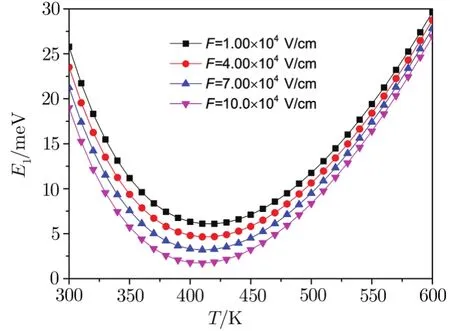
Fig.1 First-excited state energy E1versus temperature T and electric field F.
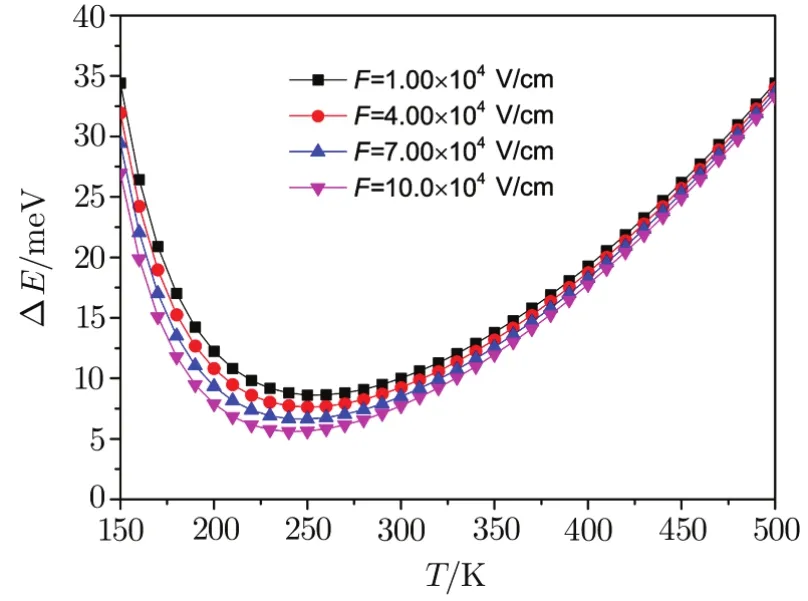
Fig.2 Excitation energy ΔE versus temperature T and electric field F.
From Figs.1–3,we found that the FESE,excitation energy and transition frequency decrease with increasing temperature in the region of lower region,and increase with temperature in the higher temperature region.As the temperature is increased,the e-p velocities are accelerated,and then more electrons interact with more phonons.In the lower temperature region,the contribution from the increased electron velocity that makes more electrons to locate on the ground-and first-excitedstates is smaller than that from the electrons interacting with more phonons.Moreover,the contribution destructs these states.Thus the FESE,the excitation energy and transition frequency are reduced.In the region of higher temperature,however,the contributions come from the electron velocity is larger than from the e-p interaction,leading to the enhancement of the above three physical quantities.
As also seen in Figs.1–3,the FESE,excitation energy and transition frequency decrease with the increase of the electric field strength.As the introduction of electric field corresponds to induce a new confinement on the electron,which leads to greater electron wave-function overlapping with each other,the electron energy and the e-p interactions will be amplified,and the FESE,excitation energy and transition frequency are increased.However the last term in Eq.(7)and the last two terms in Eq.(8)are the contributions of the electric field to the FESE and the excitation energy,which are negative values.However the total FESE and excitation energy are positive values.Form the mathematics,as we know that they are decaying functions of the electric field.
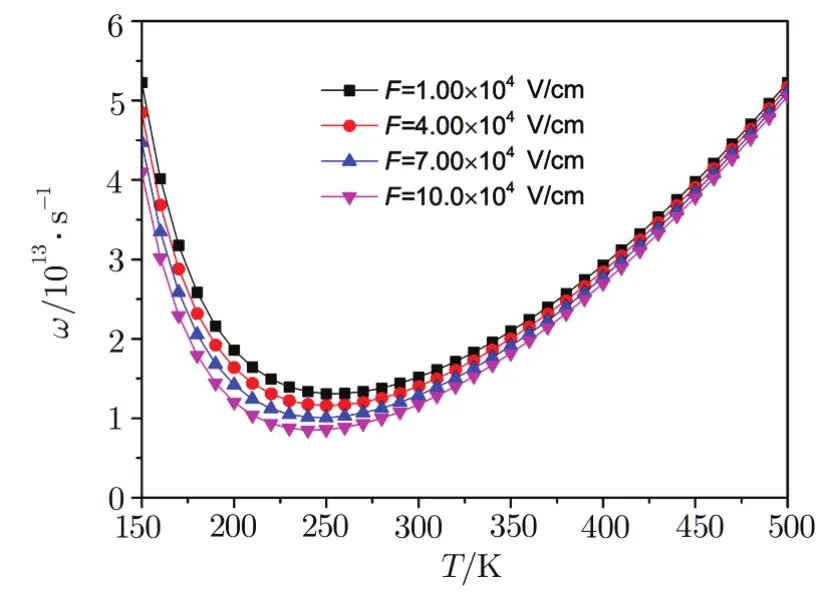
Fig.3 Transition frequency ω versus temperature T and electric field F.
Here we suggest two methods to control the FESE,excitation energy and transition frequency of the strong coupling polaron in the CsI QPD:adjusting the temperature and adjusting the electric field.
In summary,the temperature,PHP and electric field are important physics factors to research the polaron properties in a CsI QPD.
4 Conclusion
The temperature effects of electric field on the FESE,excitation energy and transition frequency of the strongly coupled polaron in the CsI QPD have been investigated by using QST and VMPT.It shows that the FESE,excitation energy and transition frequency decrease(increase)with increasing temperature in region of lower(higher)temperature,and they decreased with enhancing electric field.This study suggests that the temperature,the PHP and the electric field are important physics factors to study the polaron properties in a CsI QPD.
[1]R.Anufriev,J.B.Barakat,G.Patriarche,et al.,Nanotechnology 26(2015)395701.
[2]N.Vainorius,S.Lehmann,A.Gustafsson,et al.,Nano Lett.16(2016)2774.
[3]L.Kinnischtzke,K.M.Goodfellow,C.Chakraborty,etal.,Appl.Phys.Lett.108(2016)211905.
[4]M.Prost,M.E.Kurdi,F.Aniel,et al.,J.Appl.Phys.118(2015)125704.
[5]V.Preisler,T.Grange,R.Ferreira,et al.,Phys.Rev.B 73(2006)3881.
[6]S.J.Xu,G.Q.Li,Y.J.Wang,et al.,Appl.Phys.Lett.88(2006)083123.
[7]L.Jacak,J.Krasnyj,D.Jacak,and P.Machnikowski,Phys.Rev.B 65(2002)113305.
[8]K.M.Hung,J.Appl.Phys.102(2007)023111.
[9]O.Verzelen,R.Ferreira,and G.Bastard,Phys.Rev.B 62(2000)R4809.
[10]R.Khordad,B.Mirhosseini,and H.Bahramiyan,Opt.Quant.Electron.48(2016)122.
[11]Ning Li,Kang-Xian Guo,and Shuai Shao,Opt.Quant.Electron.44(2012)493.
[12]Yong Sun,Zhao-Hua Ding,and Jing-Lin Xiao,J.Electron.Mater.45(2016)3576.
[13]Xin-Jun Ma,Bin Qi,and Jing-Lin Xiao,J.Low Temp.Phys.180(2015)315.
[14]A.Cetin,Phys.Lett.A 372(2008)3852.
[15]S.I.Pekar,ZH.Eksp.Teor.Fiz.16(1946)341.
[16]S.I.Pekar and M.F.Deigen,ZH.Eksp.Teor.Fiz.18(1948)481.
[17]S.I.Pekar,Untersuchungen uber die Elektronentheorie der Kristalle,Akademie-Verlag,Berlin(1954).
[18]Wei Xiao,Bin Qi,and Jing-Lin Xiao,J.Low Temp.Phys.179(2015)166.
[19]Zhaohua Ding,Yong Sun,and Jinglin Xiao,Inter.J.Quant.Inf.10(2013)471.
[20]Jozef T.Devreese,Polarons in Ionic Crystals and Polar Semiconductors,North-Holland,Amsterdam(1972).
杂志排行
Communications in Theoretical Physics的其它文章
- Hypergeometric Series Solution to a Class of Second-Order Boundary Value Problems via Laplace Transform with Applications to Nanofluids
- Quantum Spin Transport in Rashba Spin-Orbit-Coupled Graphene Nanoflakes∗
- Self-similar Solution of a Cylindrical Shock Wave under the Action of Monochromatic Radiation in a Rotational Axisymmetric Dusty Gas
- Proton Beam Generated by Multi-Lasers Interaction with Rear-Holed Target
- Electrostatic Surface Waves on Semi-Bounded Quantum Electron-Hole Semiconductor Plasmas
- Solutions to Forced and Unforced Lin–Reissner–Tsien Equations for Transonic Gas Flows on Various Length Scales
