Advanced Study of Unsteady Heat and Chemical Reaction with Ramped Wall and Slip Effect on a Viscous Fluid

Ayesha Sohail,K.Maqbool,Noreen Sher Akbar,and Muhammad YounasDepartment of Mathematics,COMSATS Institute of Information technology,Lahore,Pakistan

2Department of Mathematics&Statistics,FBAS,IIU,Islamabad 44000,Pakistan

3DBS&H CEME,National University of Sciences and DBS&H CEME,National University of Sciences and Technology,Islamabad,Pakistan

Nomenclature

1 Introduction

Many researchers have been attracted to study free convective flow of MHD fluid due to its importance and applications in MHD pumps,accelerators and flow meters,aerodynamic heating,meteorology,geophysics,astrophysics,boundary layer control energy generators,petroleum industry,plasma studies,polymer technology,refinement of crude oil,and in material processing,e.g.,continuous casting wire,metal forming,glass fiber drawing,and extrusion.Purification and filtration processes in chemical industry are also the examples of convective flow through permeable medium.In agriculture engineering,itis used to study the underground water resources,and in petroleum engineering the study of flow of water,oil and natural gas through reservoirs and oil channels.

The impact of magnetic field on the study of viscous,incompressible and electrically conducting fluids has been very signifi cant in the field of science and engineering.Much research has been carried out due to the effectiveness of magnetic field on the fluid flow problems.Experimental and 3D numerical studies,to improve the understanding of the flow and heat transfer phenomena in narrow,open-ended channels have been studied in the literature.Recently,non-uniform heating con figurations,in which heat sources alternated with unheated zones on both walls were simulated by Tkachenkoet al.[1]

The steady, fully developed flow of electrically conducting non-Newtonian fluids through square microchannels have recently been studied by Kiyasatfar&Pourmahmoud,[2]they demonstrated the viscous dissipation,joule heating and MHD effects using excellent tools.Seth[3]carried out research for rotating Hartmann flow to see the effects of Hall current in the presence of inclined magnetic field.

Ostrach[4]used similarity integral transformation method in order to study transient free convective flow past a semi in finite vertical flat plate.Takar[5]studied the combined effects of thermal and mass diffusion for an unsteady free convective flow of a viscous,incompressible fluid past through an in finite vertical flat plate.Kim[6]studied the magnetohydrodynamics convective heat transfer effects with variable suction for a semi-in finite porous vertical flat plate.Darcay’s law[7]is very much important in order to study the fluid flow problems in porous medium.Brinkman[8−9]and Wooding[10]used the modified form of Darcay’s law to investigate the fluid flow problems in porous medium.

The thermal diffusion effects for an MHD free convective flow was studied by A fify[11]and Elbade[12]investigated the combined effects of mass and heat transfer for the motion of a viscous,incompressible magnetohydrodynamic fluid.

Furthermore,an extensive research has been carried out by number of researchers[13−16]in order to investigate the combined effects of heat a mass transfer for electrically conducting fluids.The combined effects of mass and heat transfer play a vital role in many fields of science and engineering e.g.,dissemination of moister and temperature over agriculture fields and orchard of fruit trees,damage of crops due to freezing,formation and sprinkling of fog,and pollution effects on the environment etc.

Moreover,there are problems of our interest which are needed to be solved using non-uniform initial and boundary conditions.In this regard,lots of research have been conducted recently.[17−22]Many people have studied electrically conducting fluids through a porous medium and MHD effects upon them due to their extensive applications in science and engineering.

Radiation is a process in which heat transforms from source to sink in the form of wave or mass particles.The study of many industrial and environmental processes based upon radiative convective flows e.g.,cooling and heating of chambers,evaporation of heat from large water sources etc.Heat and mass transfer due to radiation also plays an important role in the field of engineering science.Many researchers(Ref.[23]and the references therein)have studied the radiative effects on the convective motion of mass and heat.

The study of a fluid passing through an in finite flat vertical plate has been of great interest of many researchers and this type of motion immensely depends upon the motion of boundaries and wall shear stress.The analytic solutions of such type of problems are rare and even exceptional if the integrated effects of heat and mass transfer along with the radiative and change in concentration effects of the fluid are considered.Navier[24]suggested a particular boundary condition,such that the wall shear stress and the slip velocity are combined linearly.This leads us a different category of problems in which shear stress at the boundary,dominates the slip velocity at the wall.The issues associated with the slip flow are of great interest in science and technology.Keeping in view such ambitions Fatecau[25]investigated the porosity effects with arbitrary shear stress for the free convective motion of a fluid near a vertical wall.

Furthermore,the effects of wall shear stress on unsteady MHD conjugate flow in a porous medium with ramped wall temperature was investigated by Arshad Khan.[26]But,nobody has studied the effects of radiation and viscous dissipation,chemical reaction and Duffor,ramped concentration and ramped temperature on wall for the motion of a conjugate free convective fluid with shear stress. Different fluid model with different flow geometries was discussed in Refs.[27–33].Analytical approximation of heat and mass transfer in MHD non-Newtonian nanofluid flow over a stretching sheet with convective surface boundary conditions was provided by Freidoonimehret al.[34]They presented that their HAM solutions are in very good correlation with those previously published studies in the special cases.Baiet al.[35]presented stagnation-point heat and mass transfer of MHD Maxwell nanofluids over a stretching surface in the presence of thermophoresis.According to them the thinner velocity boundary layer thickness occurs for the larger value of the stagnation parameter.Zhanget al.[36]discussed unsteady flow and heat transfer of power-law nano fluid thin film over a stretching sheet with variable magnetic field and power-law velocity slip effect.They considered different types of nanoparticles,Al2O3,TiO2 and CuO with ethylene vinyl acetate copolymer(EVA)as a base fluid.The governing equations are solved by using DTM–NIM which is combined the differential transform method(DTM)with Newton Iteration method(NIM).

In the present work,our emphasis is to simulate the fluid dynamics,numerically for a viscous fluid passing through a vertical flat plate,under the combined effect of magnetism,radiations,chemical reaction and wall shear stress.Our CFD analysis of unsteady heat and mass transfer with ramped wall and slip effect may prove to be a benchmark for industrial applications.

2 Formulation of the Problem

Let us consider unsteady natural convective flow of MHD incompressible viscous(Newtonian fluid) fluid past a vertical plate embedded in a porous media.The temperature and concentration on the surface of a vertical plate are non uniform and slip boundary condition is considered on the surface of the vertical plate.Since the sheet is vertical soy′-axis is taken along the plate andx′-axis is taken normal to the sheet.The flow is assumed to be in the direction of the in finite plate i.e.,in the upward horizontal direction.Therefore all physical quantities velocity,temperature and concentration are function ofy′andt′.Initially for time(t′≤0) fluid is at rest with constant temperatureθ∞and concentrationC∞.At time(t′＞0)the temperature of the plate is raised or lowered toθ∞+(θw−θ∞)(t′/t0)and concentration of the plate raised or lowered toC∞+(Cw−C∞)(t′/t0).When fort′≤t0and thereafter i.e.fort′＞t0plate is maintained at the constant temperatureθwand the concentration level at the plate is raised toCwor concentration is supplied at a constant rate to the plate see Refs.[32–33].

Fig.1 Schematic Diagram.

According to the above assumption and Boussinesq’s approximation,the governing equations now take the following form.

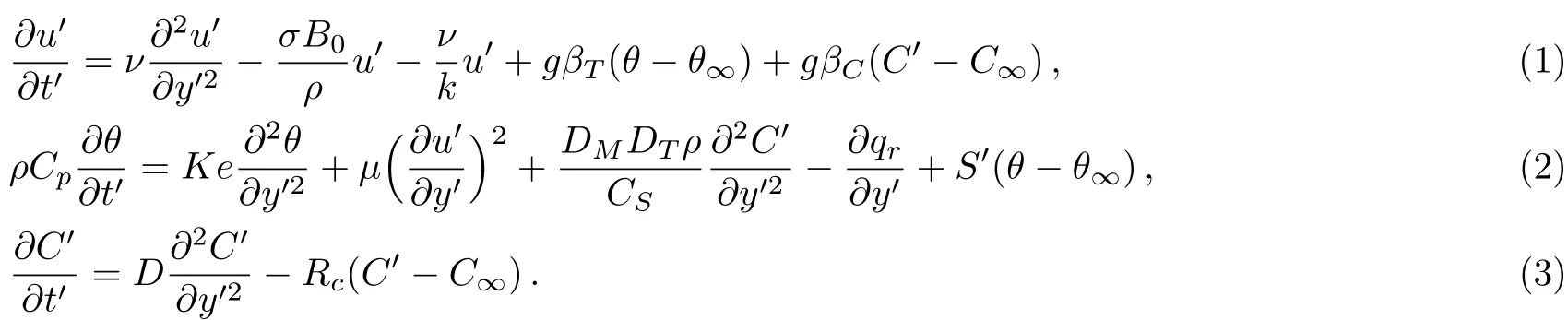
The appropriate initial and boundary conditions are as defined in Refs.[32–33]:

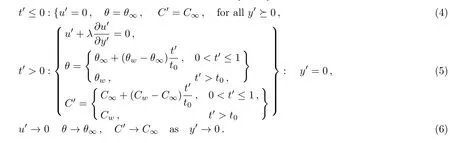
Non-dimensional quantities

Using dimensionless quantities,we get non-dimensional problem

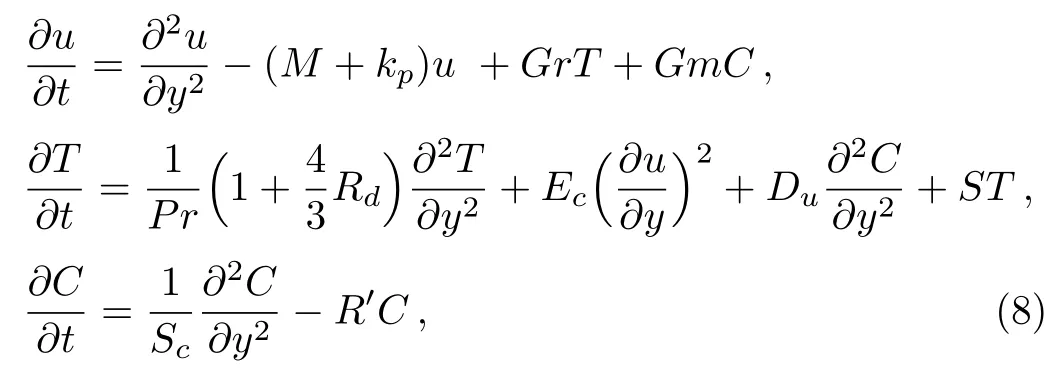
with boundary conditions as defined in Refs.[32–33].

3 Finite Element Algorithm

We have studied an incompressible and electrically conducting fluid with smaller Reynolds number.The system of equations is solved using the finite element collocation method.This technique is employed since it provides more accurate solutions to the set of equations as verified by Refs.[30–31].Our numerical technique uses the piecewise polynomials for the trial function space.Next the time integration has been conducted with the help of the most commonly used technique,which is generalization of the usual method for treating time dependent partial differential equations.

The first step involved while implementing the finite element collocation method is the selection of the piecewise polynomials.The development of such a code,depending on polynomials,is usually initiated with a single partial differential equation.

4 Results and Discussions

In order to understand the physical aspects of the problem,we have solved it numerically and found out relations for velocity,concentration and temperature pro files,rate of transformation of heat as a function of Nusselt number,rate of mass transfer as a function of Sherwood number,coefficient of skin friction by assigning different values to the parameters involvedM,Gm,Gr,Du,Sc,Pr,K,tetc.

3D visualization of velocity,temperature and concentration are presented in Figs.2,3,4.The change in velocity profile against different values of Hartmann number is shown in Fig.5.Dotted and continuous curves are drawn against variable and constant temperatures respectively.We observed from the figure that by increasing the Hartmann number,the velocity profile is going to decrease.This shows that Hartmann number act as a retarding force on free-convective motion of the fluid.Figure 6 shows the velocity profile relative to different values of Grashof number.The curves drawn in the graph show that by increasing the values ofGr,the velocity profile is going to increase due to increase in buoyancy force.The plots in Fig.7 showing the velocity pro file against different values ofGm,the rate of mass transfer.The plots in this figure show that velocity profile increases as we increase the values of Grashof number.

Fig.2 3D visualization of the concentration.

Fig.3 3D visualization of the temperature.

Fig.4 3D visualization of the velocity.

The velocity pro file for different values ofSc,are shown in Fig.8,which shows that velocity profile increase as we increase the Schmidt number.This is due to the fact of increase in the momentum boundary layer of the fluid.

Fig.5 Effect of M=5,10,15,20 on u(y,t)if Gr=2,Pr=0.7,Gm=2,Rd=1,Kp=1,Ec=0.3,S=1,Du=0.1,Sc=0.6,R′=0.1,η=0.1.

Fig.6 Effect of Gr=0,2,5,7 on u(y,t)if M=10,Pr=0.7,Gm=2,Rd=1,Kp=1,Ec=0.3,S=1,Du=0.1,Sc=0.6,R′=0.1,η=0.1.

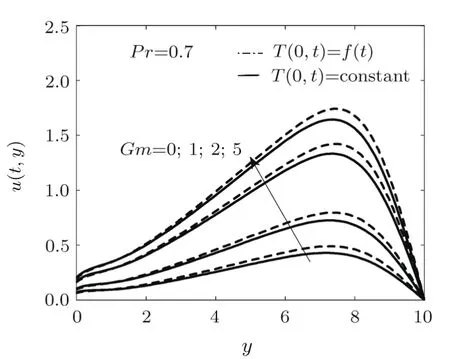
Fig.7 Effect of Gm=0,1,3,5 on u(y,t)if Gr=2,Pr=0.7,M=10,Rd=1,Kp=1,Ec=0.3,S=1,Du=0.1,Sc=0.6,R′=0.1,η=0.1.

The profile of concentration for different values of Prandtl number is shown in Fig.9.Clearly it is analyzed that concentration profile decreases by the increase of Prandtl number.Furthermore,the effects of Prandtl number on the thermal boundary layer thickness is shown in Fig.10.It is observed that with the increase of Prandtl number the boundary layer thickness reduces which ultimately reduces the average temperature.

Fig.8 Effect of Sc on u(y,t)if Gr=2,Pr=0.7,M=10,Rd=1,Kp=1,Ec=0.3,S=1,Du=0.1,R′=0.1,η=0.1.

Fig.9 Effect of Pr=0.7,1,3,7 on C(y,t)if Gr=2,M=1,Gm=2,Rd=1,Kp=1,Ec=0.3,S=1,Du=0.1,Sc=0.6,R′=0.1,η=0.1.

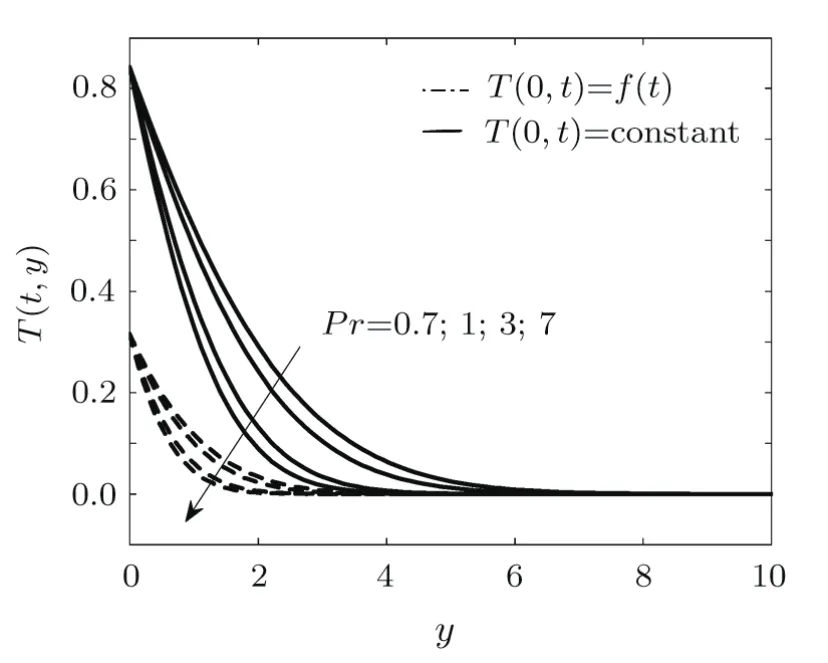
Fig.10 Effect of Pr=0.7,1,3,7 on T(y,t)if Gr=2,M=1,Gm=2,Rd=1,Kp=1,Ec=0.3,S=1,Du=0.1,Sc=0.6,R′=0.1,η=0.1.

Figure 11 showing velocity profile for different values of radiation parameterRd.The plots in this figure show that velocity increases with the increase of radiation parameterRd.Actually,for a fixed value ofPr,the energy in the form of radiation given to the fluid will wholly be used to increase its kinetic energy which ultimately results in the increase of velocity.

Fig.11 Effect of Rd=0,1,2,5 on u(y,t)if Gr=2,Gm=2,M=1,Kp=1,Ec=0.3,S=1,Du=0.1,Sc=0.6,R′=0.1.

Fig.12 Effect of Du=0.1,0.3,0.5,1 on T(y,t),Gr=2,Gm=2,Rd=1,Kp=1,Ec=0.3,S=1,M=1,Sc=0.6,R′=0.1.

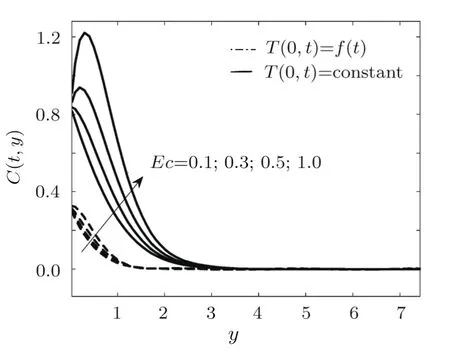
Fig.13 Effect of Ec=0.1,0.3,0.5,1 on C(y,t)if Gr=2,Gm=2,Rd=1,Kp=1,Ec=0.3,S=1,M=1,Sc=0.6,R′=0.1.

We know the Dufour effect gives us the change in enthalpy due to change in concentration of the fluid.Figure 12 illustrates the effects on temperature profile due to change in Dufour number.We can see that temperature increases by increasing the values of Dufour number.The plots in Fig.13 showing the concentration profile for different values of Eckert number.It is analysed from these plots that by increasing the values ofEc,concentration profile also increases.

The comparison of change in temperature profile with respect to change in the dimensionless Schmidt number,Sc,is shown in Fig.14.The curves in this plot show the rise in temperature profile as there is an increase in the Schmidt number.Furthermore,the plots in Fig.15 showing the change in concentration profile against Schmidt number.It is evident from the plot that concentration increases by the increasing the dimensionless Schmidt number.

Fig.14 Effect of Sc=0.1,0.3,0.6,0.9 on T(t,y)if Gr=2,Pr=0.7,Gm=2,M=1,Kp=1,Ec=0.3,Rd=1,Du=0.1,S=1,R′=0.1,η=0.1.

Fig.15 Effect of Sc=0.1,0.3,0.6,0.9 on C(y,t)if Gr=2,Pr=0.7,Gm=2,M=1,Kp=1,Ec=0.3,Rd=1,Du=0.1,S=1,R′=0.1,η=0.1.

The skin friction plays an important role in thermal and engineering processes,since it is a friction between the surface of a moving solid through a fluid and the fluid itself or between a moving fluid and its surrounding surface.It is depicted from Fig.16 that skin friction decreases with increasing values of magnetic parameter and slip parameter.

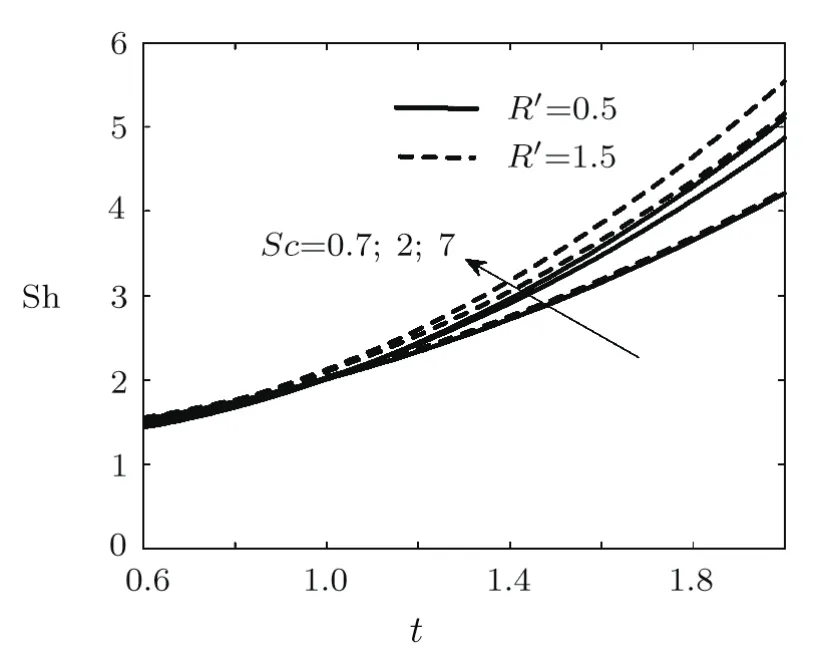
Fig.16 Skin friction coefficient relative to change in slip parameter,η and Pr.

Fig.17(a)Nusselt number(left)relative to change in S and Pr(b)Sherwood number(right)relative to change in the parameters Sc and R′.

Nusselt Number is defined as the ratio of heat transfer by convection to the heat transfer by conduction when a fluid past through a solid surface.

The numerical results for Nusselt number are presented in Fig.17,according to our calculations,the Nusselt number tends to decrease with increasing values of Prandtl number.Further,it is observed that the Sherwood number,which is in fact the ratio of rate of actual mass transfer to the rate of mass transfer through diffusion,increases with increasing Schmidt number.

5 Conclusion

The study considered here presents numerical analysis of unsteady free convective heat and mass transfer flow of a viscous incompressible fluid past through a vertical plate embedded in a porous media with ramped wall temperature and concentration in the presence of radiation,chemical reaction,viscous dissipation,Duffor and slip effects.The results obtained show that the velocity increases with increasing values of the radiation parameter,Grashof number,modified Grashof number.However,the skin friction is decreased when slip and magnetic parameters are increased.The Nusselt number decreases with the increasing values of Prandtl number.The Sherwood number increases with the increasing values of Schmidt number.With the help of the finite element analysis,we have obtained the solution of a complex fluid problem which is important from the engineering perspective and can prove to be a benchmark while studying the thermophysical properties of viscous fluids at the laboratory level.

[1]O.A.Tkachenko,V.Timchenko,S.Giroux-Julien,et al.,International Journal of Thermal Sciences 99(2016)9.

[2]M.Kiyasatfar and N.Pourmahmoud,International Journal of Thermal Sciences 99(2016)26.

[3]G.S.Seth,R.Nandkeolyar,and M.S.Ansari,Tamkang Journal of Science and Engineering 13(2010)243.

[4]S.Ostrach,An Analysis of Laminar Free Convection Flow and Heat Transfer About a Flat Plate Parallel to the Direction of the Generating Body Force,Technical Note,NACA Report,Washington 39(1953)63.

[5]H.S.Takhar,S.Roy,and G.Nath,Heat Mass Transfer 39(2003)825.

[6]Y.J.Kim,International Journal of Engineering 38(2000)833.

[7]H.P.G.Darcy,Lee Fort Airs Publication La Villede Dijan Victor Dalonat,Paris 1(1857)41.

[8]H.C.Brickman,Applied Sciences Research A1(1947)27.

[9]H.C.Brickman,Applied Sciences Research A1(1947)81.

[10]R.Wooding,Journal of Fluid Mechanics 2(1957)273.

[11]A.A.Afify,Communication in Nonlinear Science and Numerical Simulation 14(2009)2202.

[12]N.T.M Eldabe,E.A.Elbashbeshy,M.A.Elsayed,W.S.A.Hasanin,and E.M.Elsaid,International Journal of Energy Technology 3(2011)1.

[13]M.A.Hossain and A.C.Mandal,Journal of Physics D 18(1985)163.

[14]B.K.Jha,Astrophysics Space Science 175(1991)283.

[15]E.M.A.Elbashbeshy,International Journal of Engineering Science 34(1997)515.

[16]A.J.Chamkha and A.R.A.Khaled,International Journal of Numerical Methods for Heat and Fluid Flow 10(2000)455.

[17]P.Chandrakala,International Journal of Dynamical Fluids 7(2011)1.

[18]S.S.Das,S.Parija,R.K.Padhy,and M.Sahu,International Journal of Energy Environment 3(2012)209.

[19]S.S.Das,M.Maity,and J.K.Das,International Journal of Energy Environment 3(2012)109.

[20]M.Narahari and A.Ishaq,Journal of Applied Sciences 11(2011)1096.

[21]M.Narahari and M.Y.Nayan,Turkish Journal of Engineering Environmental Sciences 35(2011)187.

[22]A.Hussanan,I.Khan,and S.Sharidan,Journal of Applied Mathematics,Article ID 2013(2013)1.

[23]S.Das,M.Jana,and R.N.Jana,Open Journal of Fluid Dynamics 1(2011)1.

[24]C.L.M.H.Navier,Mem.Acad.R.Sci.Inst.Fr.6(1827)389.

[25]C.Fetecau and M.Rana,Zeitschrift für Naturforschung A 68(2014)130.

[26]A.Khan,I.Khan,F.Ali,S.Ulhaq,and S.Shafie,PLOS ONE 9(2014)3.

[27]R.Ellahi,Shafiq Ur Rahman,S.Nadeem,and K.Vafai,Commun.Theor.Phys.63(2015)353.

[28]A.Ebaid,Phys.Lett.A 372(2008)5321.

[29]R.Ellahi,M.Mubeshir Bhatti,C.Fetecau,and K.Vafai,Commun.Theor.Phys.65(2016)66.

[30]D.Clouteau,M.L.Elhabre,and D.Aubry,Comput.Mech.25(2000)567.

[31]A.Logg,K.A.Mardal,and G.Wells,Automated Solution of Differential Equations by the Finite Element Method:The FEni CS Book,Springer Science&Business Media,84(2012)44.

[32]M.Narahari,O.A.Bég,and S.K.Ghosh,World Journal of Mechanics 1(2011)176.

[33]S.Ul Haq,I.Khan,F.Ali,A.Khan,T.Nabil,and A.A.Hameed,Influence of Slip Condition on Unsteady Free Convection Flow of Viscous Fluid with Ramped Wall Temperature,Abstract and Applied Analysis Article ID 327975,(2016)in press.

[34]N.Freidoonimehr,M.M.Rashidi,M.H.Momenpour,and S.Rashidi,International Journal of Biomathematics 10(2017)1750008[25 pages].

[35]Y.Bai,X.Liu,Y.Zhang,and M.Zhang,Journal of Molecular Liquids 224(2016)1172.

[36]Y.Zhang,M.Zhang,and Y.Bai,Journal of the Taiwan Institute of Chemical Engineers 70(2017)104.