Quantum Fisher Information of Driven Multi-particle Systems in Structured Bosonic Reservoirs∗

Kai Yan(严凯),Yan-Qing Xie(谢燕青),Yu-Meng Huang(黄雨梦),and Xiang Hao(郝翔)

Department of Physics,School of Mathematics and Physics,Suzhou University of Science and Technology,Suzhou 215009,China

1 Introduction

The quantum Fisher information(QFI)is a key quantity in quantum metrology,which decides the precision of parameter estimation according to the quantum Cramér–Rao inequality.[1−2]Recently,QFI has been widely studied in many fields which include the investigation of uncertainty relations,[3−4]the estimation of quantum speedup limit time,[5]the characterization of quantum phase transition,[6]and the detection of entanglement.[7]Until now,other enlightening works have also considered the Unruh effect on quantum metrology in the non-inertial frame.[8−13]For a highly sensitive quantum measurement for a parameter,a series of protocols on enhancing QFI have been put forward before.The correlated states can improve the precision of parameter estimation.[14−25]The NOON states[22−24]and squeezed states[20,25]can break through the shot noise limit(also called the standard quantum limit).It was demonstrated that the maximally entangled states and coherent ones can reach the Heisenberg limit.[17,19,26]

Moreover,the system of interest is usually considered to be open because of the interaction between the system and surrounding environments.Some schemes about open systems have been presented.[18−19,26−34]The quantum parameter estimations in the spin-Boson model with a driven field[18]and finite-temperature resorvior[19]are studied.The quantum estimation has been investigated in spin environments.[27−29]The above schemes motivate us to consider the effects from both entanglement and realistic environments on the parameter estimation.In this paper,we focus on the study of the QFI of the maximally entangled states in many atoms coupled to local bosonic reservoirs at low temperatures.The open system is described by the famous spin-boson model which can be referred to as an effective two-level system coupled to a bosonic reservoir.[35]The model has extensively been applied to noisy quantum dots,[31]decoherence of qubits in quantum computation,[32−33]quantum impurities and charge transfer in donor-acceptor systems.[34]

The paper is organized as follows.In Sec.2,we give a brief introduction of QFI.In Sec.3,the dynamics of a two-level atom driven by a classical field in a finitetemperature structured environment is derived.In Sec.4,we calculate the QFI ofNindependent atoms which are initially at the maximally entangled state.Each atom locally interacts with a structured bosonic reservoir.The effects of quantum entanglement on the parameter estimation are analyzed in Sec.5.Finally,a simple discussion is concluded.

2 Quantum Fisher Information

A generalized measurement is described by a collection of non-negative operatorswhich satisfy the completeness equation,[36]The quantityξlabels the result of the measurement.is a unit operator.With respect to a given parameterθ,the probability for the resultξisp(ξ,θ)=Tr(ˆE(ξ)ˆρ(θ)).Considering an unbiased estimatorˆθ(〈ˆθ〉=θ)related to the parameterθ,the Cramér–Rao bound on the measurement can be described by,

wherevis the number of the measurements andFcθis the Fisher information(FI)related to the parameterθ.Maximizing over all measurements,the quantum Fisher information(QFI)[1−2]is defined as,

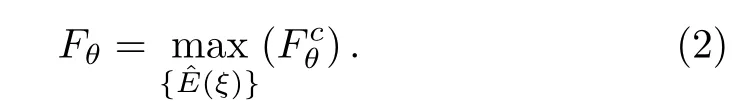
Obviously,the variance of parameterθhas a lower bound,[1−2]

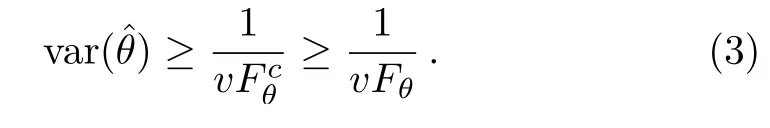
In accordance with the quantum Cramér–Rao theorem,[1−2]it is proved that the increase of QFI can enhance the precision of the parameter estimation.

By the so-called symmetric logarithmic derivative(SLD)Lθsatisfying the relation

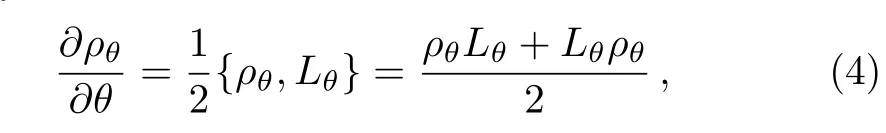
the expression of the QFI can be written as,[1−2]

Because the density operatorρθis a H∑ermitian operator,it has a spectral decompositionρθ=Npi|φi〉〈φi|,

i=1i.e.,the density operatorρθis written as{pi,|ψi〉},with the eigenvaluespiand corresponding normalized eigenvectors|ψi〉.Takingρθinto Eq.(4)and Eq.(5),Lθ(SLD)andFθ(QFI)can be expressed as[37−39]

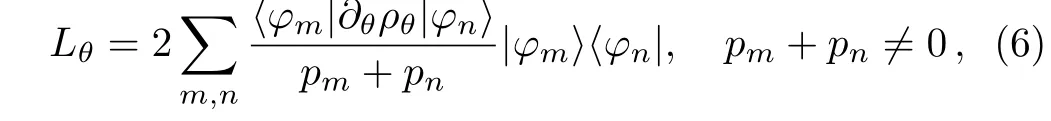
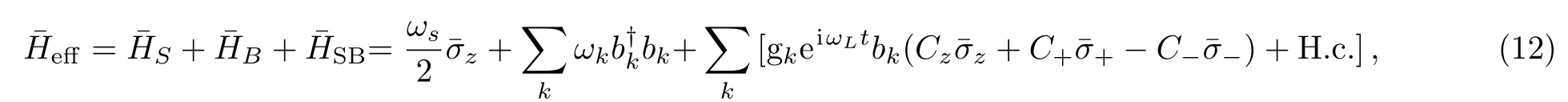
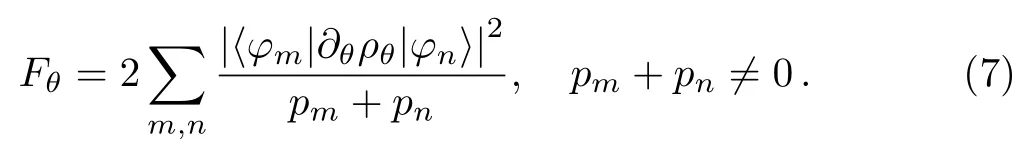
In fact,the dynamics of quantum Fisher information can be determined by the evolution of the density matrix of quantum system.

3 The Hamiltonian and Quantum Master Equation

We consider a typical spin-boson model which is described by a two-level atom locally interacting with bosonic reservoir at a low temperatureT.The atom can be driven by a monochrome classical field with the frequencyωL.In the rotating reference frame,the total Hamiltonian of the open system can be written as:[19,35,40]

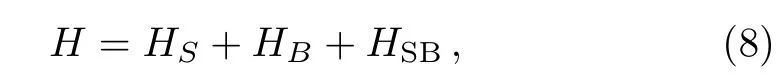
where

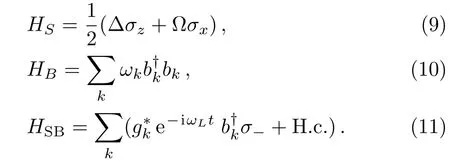
The parameter Δ =|ω0−ωL|.ω0is the transition frequency of the atom,and Ω denotes the Rabi frequency,which describes the effective coupling strength between the atom and the driven field.σx,y,zare the Pauli operators,σ±the inversion operators,(bk)the creation(annihilation)operation,andgk(g∗k)the coupling strength between the atom and the Bosonic reservoir.H.c.denotes the Hermitian conjugation of the former.

By diagonalizing the free HamiltonianHs,one can get the effective Hamiltonian in the dressed-state basis,reads as

withσ¯x,y,zandσ¯+(σ¯−)are the new Pauli operations and inversion in the dressed-state,ωs=Ω2+Δ2is the dressed-state frequency.The coefficients satisfy thatC+=cos2(η/2),C−=sin2(η/2),Cz=(1/2)sinη,whereη=arctan(Ω/Δ).In the interaction picture,the interaction Hamiltonian is equivalently transformed into

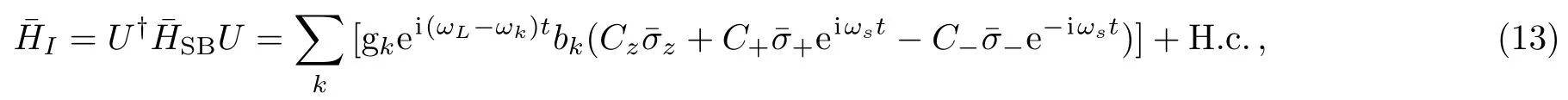
where the unitary transformation is given byU=

e−i(H¯S+H¯B)t.

According to the time-convolutionless projection operator technique,a general master equation is obtained by

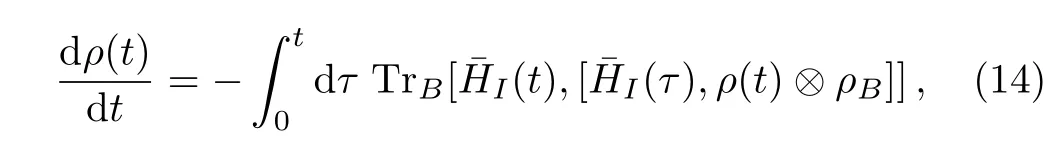
whereρ(t)is the reduced density operator of the system andρBrepresents the density matrix of the initial state of the reservoir.By taking Eq.(13)into Eq.(14),we can get the master equation in the form of

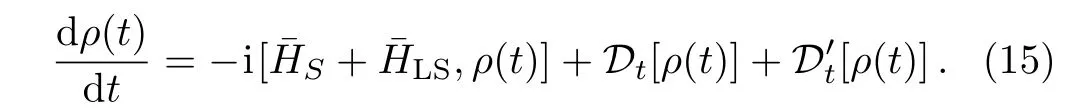
In the above equation,the parameters Γlandare determined by

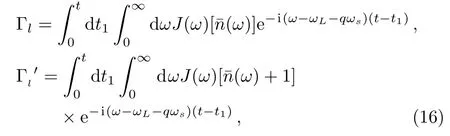
with the indexl={+,−,z}→q={1,−1,0}.The average photon number denotesn¯(ω)=1/[exp(ħω/kBT)−1].In the limit of a continuum of modes of the environment,the spectral densityJ(ω)readsdenotes secular motion of the system,in the Lindblad form,

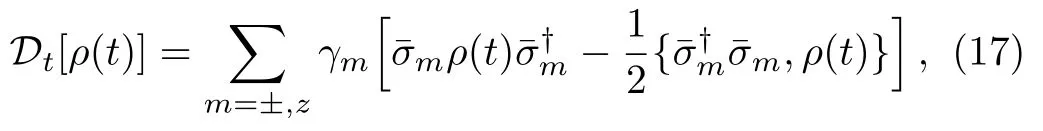
where the time-dependent parameters

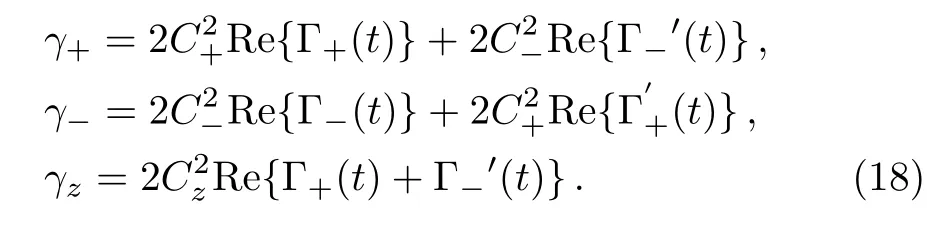
Here the notation Re is the real part of the parameter.Dt′[ρ(t)]denotes nonsecular motion of the system,which is not Lindblad form.[41]Under the secular approximation,[35]Dt′[ρ(t)]is ignored,because it has trivial effects on the dynamic of the system in the case of weak couplings.

We can use the Bloch vector to describe the arbitrary state of the system.According to the master equation,the three components of the vectorBi=Tr[ρσi](i=x,y,z)satisfy

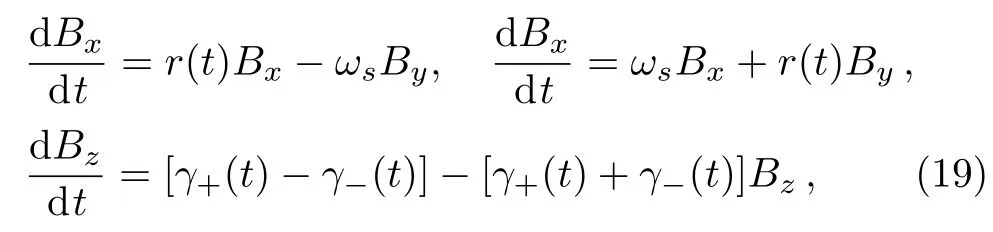
with

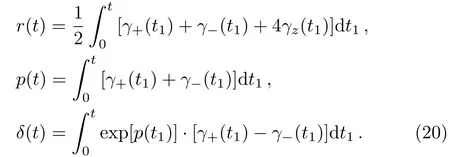
By solving the above differential equations,the three components at any timetis given by

the density operator of single-qubit though Bloch vector is written as

It is shown that the parametersr(t),p(t),δ(t)involved in the decaying rates play a key role in the dynamics of the density operatorρ(t)of the system.

4 The Dynamics of QFI forN-Particle System

The dynamics ofNindependent atoms each locally interacting with its own reservoir can be obtained by the single-atom dynamics.[42]The evolution of one atomjfrom initial stateρj(0)toρj(t)could be expressed by super-operatorε(t)asρj(t)=ε(t)·[ρj(0)].For an arbitrary initial state ofN-particle system,the expression ofρT(0)can be written as

withcii′,jj′,...,kk′is the element of the density matrixρT(0)in the postion|i,j,···k〉〈i′,j′,···k′|and all indice{i,i′,j,j′,...}={0,1}.|i〉,|j〉,...,|k〉denote the basis vector of atom 1,2,...,N,respectively.Because each atom independently interacts wich each reservoir,the state at any timeρT(t)can be expressed as

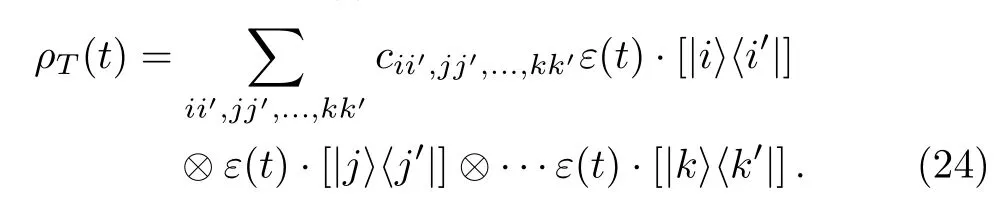
Using Eqs.(21)and(22),we can obtain the form ofε(t)·[|i〉〈i′|]as

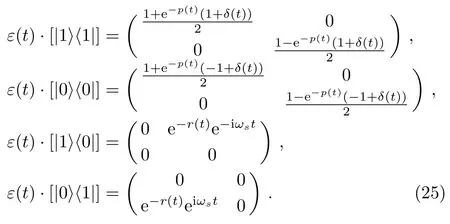
We assume that theN-particle system is initially in themaximally entangled state,i.e.,The density matrix of the total system can be written as,

whereh=exp[−r(t)],the diagonal elementai+biis given by

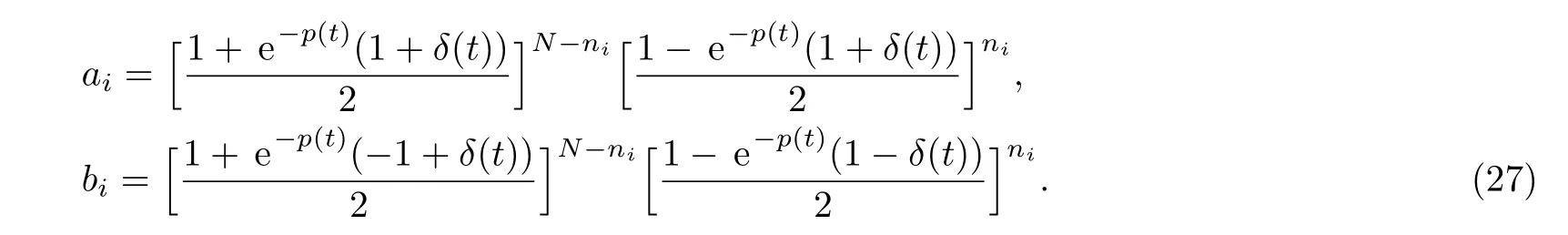
The indexi={1,2,...,2N}.The parameterniis obtained by

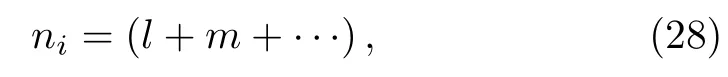
where the series of binary number(l,m,...)are determined by converting the the decimal numberi−1 into anN-bit binary number.In the case ofN=2,the parametersniare calculated asn1=(0+0),n2=(0+1),n3=(1+0),andn4=(1+1).

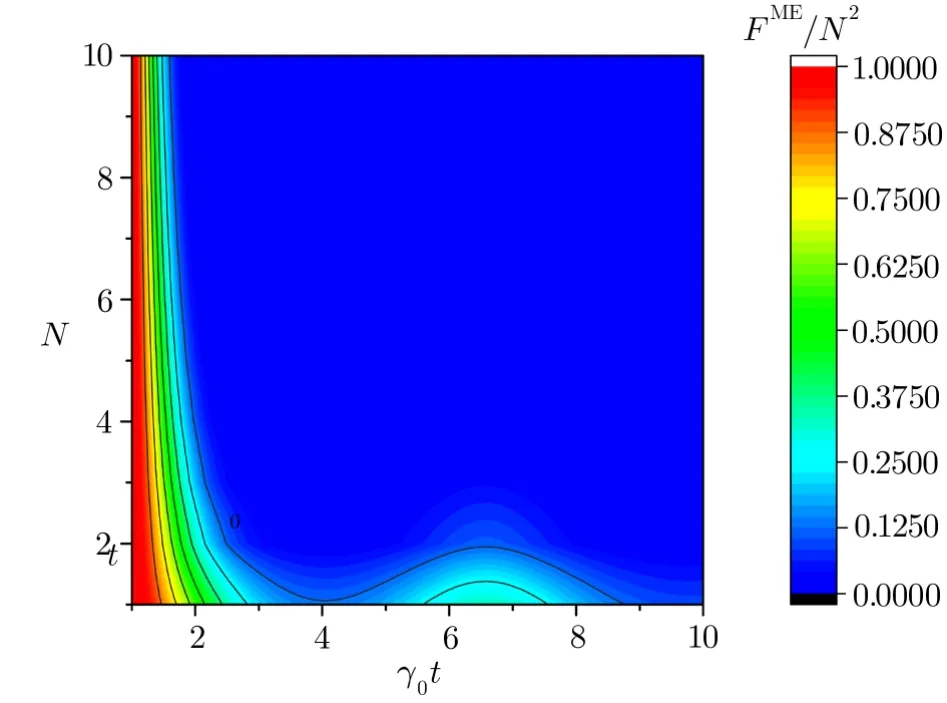
Fig.1 (Color online)The dynamics of FME/N2is plotted as a function of γ0t and N when the parameters are chosen to be λ =0.01γ0,ω0=1.1γ0,ωL= γ0,Δ =0,Ω =100γ0,T=0.01.

According to Eq.(7),the quantum Fisher information of the maximally entangled atoms is calculated as,

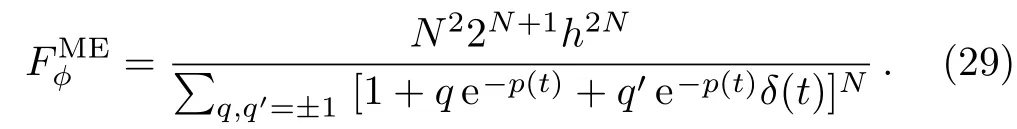
For the numerical calculation of the QFI,we consider the structured Bosonic environment which is described by the Lorenztian-type spectral density function of

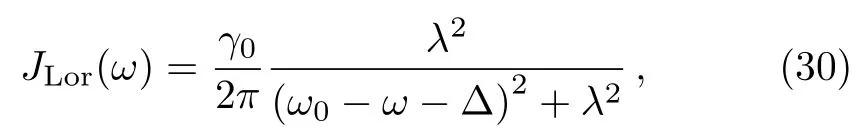
whereγ0is the decay constant under the Markovian limit andλis the spectral half width. Δ characterizes the detuning quantity between the transition frequency of the atom and central frequency of the environment.From Eq.(29),we find that the QFI ofN-particle entangled atom is proportional to the maximum valueN2which satisfies the Heisenberg limit.To further demonstrate the impacts of the structured Bosonic environment on the QFI,we plot the coefficientFME(ϕ)/N2as a function of time and the number of atoms in Fig.1.It is seen that the values of QFI are rapidly decreased with time for a large number of entangled atoms.Morover,the revivals of QFI exist whenNis small,which is related to the environmental memory effect.During a short interval,the high values of QFI can be obtained,which also prove the improved efficiency of the protocol based on quantum entanglement.

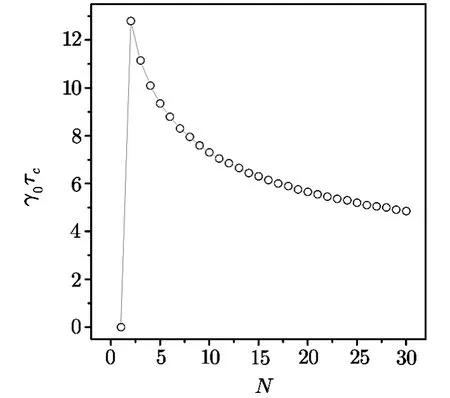
Fig.2 The characteristic time γ0τcis plotted as a function of N when the parameters are chosen to be λ =0.01γ0,ω0=1.1γ0,ωL= γ0,Δ =0,Ω =100γ0,T=0.01.

Compared with the protocol based on entangled states,theN-particle product stateis also thought of as the estimated state.In this case,the QFI is obtained as

which reaches the standard quantum limit.We can define a characteristic timeτcwhich represents the time from the Heisenberg limit(F=N2)to quantum standard limit(F=N).The value ofτcis determined by

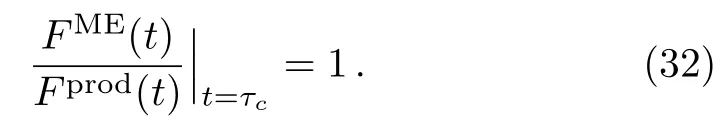
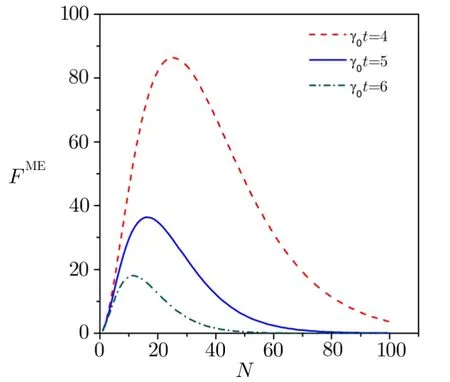
Fig.3 For some given times,the values of FMEare numerically calculated and plotted as a function of N when the parameters are chosen to be λ =0.01γ0,ω0=1.1γ0,ωL= γ0,Δ =0,Ω =100γ0,T=0.01.From the upper line to bottom one,the given times are γ0t=4,5,6.

When the evolved timet＜τc,the result ofFME＞Fprodis satisfied.It is shown that the improved efficiency of the entangled-state protocol can be maintained at an interval oft＜τc.The characteristic time as a function ofNis numerically depicted in Fig.2.We see that the values ofτcare almost decreased with increasing the number of atoms.τccan reach a maximal value whenNis small.To further investigate the effect of the number of entangled atoms on QFI,we numerically calculate QFI as a function ofNat a given time.Figure 3 shows that the values of QFI can arrive at a maximal value where the number of entangled atoms is chosen to the optimal valueNopt.The relation ofNoptwith the time is clearly shown in Fig.4.When the evolution time is short,a large number of entangled atoms is helpful for the high precision.However,because multipartite entanglement of large systems is easily destroyed by the environment,the optimal number of entangled atoms is rapidly decreased with the increase of time.If the selected time is long enough,multipartite entanglement cannot enhance the parameter estimation.

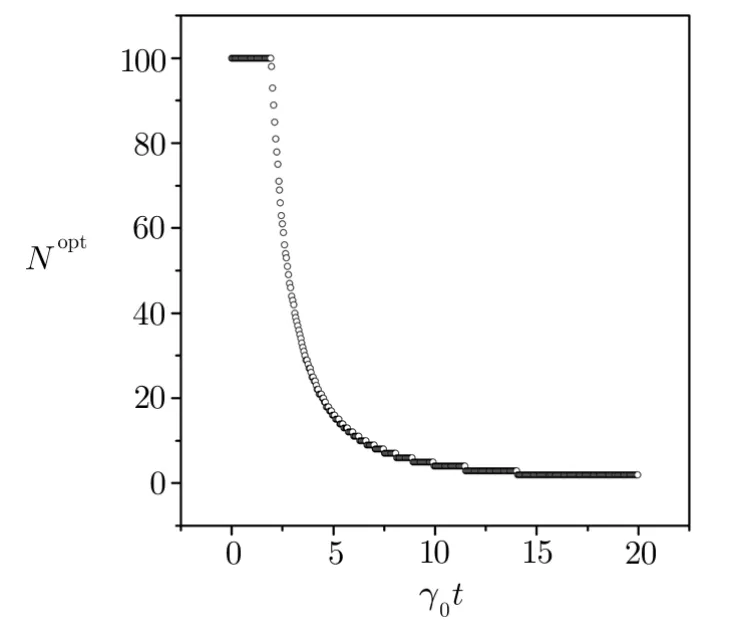
Fig.4 The optimal number of entangled atoms Noptis plotted as a function of the time γ0t when the parameters are chosen to be λ =0.01γ0,ω0=1.1γ0,ωL= γ0,Δ =0,Ω =100γ0,T=0.01.

5 Discussion

The dynamics of the parameter estimation for the driven entangled atoms is studied when each atom independently interacts with its own structured bosonic reservoir.The dynamics of open systems can be analyzed by the time-convolutionless master equation with the secular approximation.In the protocol based on theN-particle maximally entangled state,the analytical expression of QFI can be obtained in the structured Bosonic environment.There exists the characteristic time below which the protocol based on quantum entanglement is superior to that based on the product state.It is also demonstrated that the parameter estimation of the maximally entangled state is sensitive to the environment.With the increase of the number of entangled atoms,the values of QFI decay rapidly.The maximal value of QFI can be obtained when the optimal number of entangled atoms are chosen.These results are useful for the parameter estimation about the open system.

[1]S.L.Braunstein and C.M.Caves,Phys.Rev.Lett.72(1994)3439.

[2]C.W.Helstrom,Quantum Detection and Estimation Theory,Academic,New York(1976).

[3]S.Luo,Lett.Math.Phys.53(2000)243.

[4]P.Gibilisco,D.Imparato,and T.Isola,J.Math.Phys.48(2007)072109.

[5]M.M.Taddei,B.M.Escher,L.Davidovich,and R.L.de Matos Filho,Phys.Rev.Lett.110(2013)050402.

[6]C.Invernizzi,M.Korbman,L.C.Venuti,and M.G.A.Paris,Phys.Rev.A 78(2008)042106.

[7]S.Boixo and A.Monras,Phys.Rev.Lett.100(2008)100503.

[8]M.Aspachs,G.Adesso,and I.Fuentes,Phys.Rev.Lett.105(2010)151301.

[9]Y.Yao,X.Xiao,L.Ge,X.Wang,and C.Sun,Phys.Rev.A 89(2014)042336.

[10]D.Hosler and P.Kok,Phys.Rev.A 88(2013)052112.

[11]M.Ahmadi,D.E.Bruschi,N.Friis,C.Sab´In,G.Adesso,and I.Fuentes,Sci.Rep.4(2014)4996.

[12]Z.Tian,J.Wang,H.Fan,and J.Jing,Sci.Rep.5(2015)7946.

[13]X.Hao and Y.Z.Wu,Ann.Phys.372(2016)110.

[14]Xiao-Ming Lu,Xiao-Guang Wang,and C.P.Sun,Phys.Rev.A 82(2010)042103.

[15]D.J.Wineland,J.J.Bollinger,W.M.Itano,and F.L.Moore,Phys.Rev.A 46(1992)11.

[16]C.Sparaciari,S.Olivares,and G.A.Paris Matteo,Phys.Rev.A 93(2016)2.

[17]D.Leibfried,M.D.Barrett,T.Schaetz,et al.,Science 304(2004)1476.

[18]Yan-Ling Li,Xing Xiao,and Yao Yao,Phys.Rev.A 91(2015)052105.

[19]Xiang Hao,Ning-Hua Tong,and Shiqun Zhu,J.Phys.A:Math.Theor.46(2013)355302.

[20]Shao-Xiong Wu,Chang-Shui Yu,He-Shan Song,Phys.Lett.A 379(2015)1197.

[21]Jing Liu,Xiao-Ming Lu,Zhe Sun,and Xiaoguang Wang,J.Phys.A:Math.Theor.49(2016)115302.

[22]K.J.Resch,et al.,Phys.Rev.Lett 98(2007)223601.

[23]J.Joo,W.J.Munro,and T.P.Spiller,Phys.Rev.Lett.107(2011)083601.

[24]J.A.Dunningham,K.Burnett,S.M.Barnett,Phys.Rev.Lett.89(2002)150401.

[25]L.Pezzé and A.Smerzi,Phys.Rev.Lett.110(2013)163604.

[26]J.J.Bolinger,Wayne M.Itano,and D.J.Wineland,Phys.Rev.A 54(1996)R4649.

[27]X.Hao and Y.Z.Wu,AIP Advance 6(2016)045106.

[28]Heng-Na Xiong and Xiaoguang Wang,Phys.A 390(2011)4719.

[29]Y.Israel,Y.Rosen,and Y.Silberberg,Phys.Rev.Lett.112(2014)103604.

[30]J. Kacprowicz, R. Demkowicz-Dobrzanski, W.Wasilewski,K.Banaszek,andI.A.Walmsley,Nature Photon.4(2004)357.

[31]K.Le Hur,Phys.Rev.Lett.92(2004)196804.

[32]M.Thorwart and P.H¨anggi,Phys.Rev.A 65(2001)012309.

[33]T.A.Costi and R.H.McKenzie,Phys.Rev.A 68(2003)034301.

[34]S.Tornow,N.H.Tong,and R.Bulla,Europhys.Lett.73(2006)913.

[35]H.P.Breuer and F.Petruccione,The Theory of Open Quantum Systems,Oxford University Press,Oxford(2001).

[36]M.A.Nielsen and I.L.Chuang,Quantum Computation and Quantum Information,Cambridge University Press,Cambridge(2000).

[37]Alexander Holevo,Probabilistic and Statistical Aspects of Quantum Theory,Edizioni della Normale,Pisa(2011).

[38]M.G.A.Paris,Int.J.Quant.Inf.7(2009)125.

[39]Y.M.Zhang,Phys.Rev.A 88(2013)043832.

[40]P.Haikka and S.Maniscalco,Phys.Rev.A 81(2010)052103.

[41]H.P.Breuer,Phys.Rev.A 70(2004)012106.

[42]B.Bellomo,R.Lo Franco,and G.Compagno,Phys.Rev.Lett.99(2007)160502.