Non-Markovianity Measure Based on Brukner–Zeilinger Invariant Information for Unital Quantum Dynamical Maps∗

Zhi He(贺志),Lie-Qiang Zhu(朱烈强),and Li Li(李莉)

College of Physics and Electronics,Hunan Province Cooperative Innovation Center for The Construction and Development of Dongting Lake Ecological Economic Zone,Hunan University of Arts and Science,Changde 415000,China

1 Introduction

Recently,many attention has been devoted to understand and quantify the non-Markovian or memory effects of open quantum systems in theoretical research[1−2]and experimental realization.[3−7]Up to now,there may be four routes to define the non-Markovianity of open quantum systems. The first route is based on the monotonicity of physical quantity under completely positive and trace preserving(CPTP)maps,i.e.,trace distance,[8]fidelity,[9]quantum fisher information flow[10]and matrix,[11]geometry of quantum state,[12]quantum channel capacity.[13]The second route is based on the divisibility of maps of dynamical evolution.[14−18]The third route is based on the monotonicity of correlations under local quantum channels including entanglement,[15,19−20]quantum discord,[21]quantum mutual information,[22]local quantum uncertainty,[23]quantum interferometric power,[24]and multipartite correlation measures.[25]The fourth route is based on the departure between the exact two-time correlation function and one obtained from quantum regression theorem in the Born–Markov approximation.[26−27]So from different point of view,we can define various non-Markovianity measures for quantifying non-Markovian behavior of open quantum systems.

At present,for single quantum channel model,i.e.,single phase damping channel or amplitude-damping channel in Refs.[22,28],it has been shown that popular information flow characterized by trace distance,divisibility by means of Choi–Jamiolkowski isomorphism and quantum mutual information give the same non-Markovian conditions.However,for multichannel case these non-Markovianity measures including information flow,divisibility and quantum mutual information do not coincide in general,[29]i.e.,random unitary channel.[30−33]The differences between popular information flow and divisibility in quantifying non-Markovian effect of multichannel case mainly stem from two different views.The information flow indicates that the non-Markovian dynamics of quantum system is determined by joint effect of multichannel of system.However,the divisibility shows that as long as one of multichannel of system violates the divisibility of the map,the system displays non-Markovian dynamics.Therefore,for multichannel case the two famous non-Markovianity measures are obviously different.A unified non-Markovianity measure for open quantum systems is still controversial and lacking.

In present paper,based on an interesting physical quantity,namely Brukner–Zeilinger(BZ)invariant information[34]we introduce an alternative non-Markovianity measure. The measure takes advantage of non-increasing property of the BZ invariant information under completely positive and trace-preserving unitalmaps.The simplicity of computing the BZ invariant information is the main advantage of the proposed measure because of mainly depending on the purity of quantum state.The measure effectively captures the characteristics of non-Markovianity of unital dynamical maps.As some concrete application,we consider two typical non-Markovian noise channels,i.e.,the phase damping channel and the random unitary channel to show the sensitivity of the proposed measure.By investigation,we find that the conditions of detecting the non-Markovianity for the phase damping channel are consistent with the results of existing measures for non-Markovianity,i.e.,information flow,divisibility,and quantum mutual information.However,for the random unitary channel non-Markovian conditions are same to that of the information flow,but are different from that of the divisibility and quantum mutual information.The limitations of this approach also are pointed out in the paper.

The paper is organized as follows.In Sec.2,the non-Markovianity measure based on BZ invariant information for an open quantum systems is introduced.The applications of the measure to two typical non-Markovian noise channels are examined in Sec.3.Finally,we give the conclusion of our results in Sec.4.

2 Non-Markovianity via Brukner–Zeilinger Invariant Information

In 1999,Brukner and Zeilinger[34]proposed the concept of an operationally invariant measure from quantum measurements,which is essentially the quantity

where the Tr represents the trace anddis the dimension of the quantum system.As claimed in Ref.[34],theIBZ(ρ)can be treated as a quantum measure of total informational content of a given quantum state and it was successfully applied for entanglement teleportation[35]and state estimation.[36]Especially,Luo[37]has shown that the BZ invariant information is directly connected with usual quantum-mechanical variance averaged over every orthonormal basis.However,this approach was later criticized for its drawbacks.More recently,this approach reattracts people’s interest in Ref.[38],where it has been shown that some critical points can be overcome by means of natural extension or reformulation of the BZ approach.Actually,the quantityIBZ(ρ)can be also rewritten as[39]

whereρ∗=(1/d)with the identity matrixis completely mixed state and the‖ρ−σ‖2=Tr(ρ−σ)2=DHS(ρ,σ)is the Hilbert–Schmidt distance.Unfortunately,it has been shown that in Ref.[40]the Hilbert–Schmidt distanceDHS(ρ,σ)does not possess the contractivity under completely positive and trace preserving map as trace distance.[41]Therefore,it may be not proper to define the non-Markovianity by theIBZ(ρ)for open quantum systems under any completely positive and trace-preserving maps.However,more recently Rastegin[38]has also reexamined the property of theIBZ(ρ),and found that it is contract(non-increasing)under the action of bistochastic maps.Recall that a CPTP map is called a bistochastic map if it is also unital,[42]that is to say if it leaves the maximally mixed state invariant,or equally preserves identity,namely Φ(ρ∗)=ρ∗with the maximally mixed stateρ∗=(1/d),or Φ()=.Moreover,from Eq.(1)we can easily learn that the BZ invariant informationIBZ(ρ)and the purity Tr(ρ2)obeys the same contractivity under the action of bistochastic maps(or called unital maps).

According to Refs.[34,38],we give some basic properties of theIBZ(ρ)in Eqs.(1)and(2)as:

(a)TheIBZ(ρ)is invariant under unitary operation,i.e.,IBZ(UρU†)=IBZ(ρ),which is obvious from the definition of Eq.(1),namely

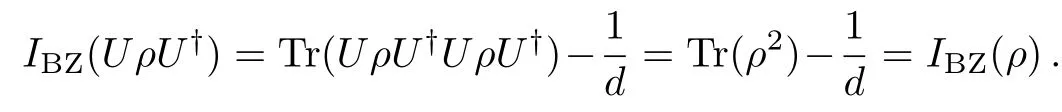
(b)TheIBZ(ρ)is contract(or called non-increasing)under any completely positive and trace preserving bistochastic(or called unital)maps the action of bistochastic maps or operations,i.e.,IBZ(Φρ)≤IBZ(ρ)for any unital map Φ.

It is clear that the property(b)of theIBZ(ρ)becomes a starting point of defining a measure based on theIBZ(ρ)to detect the non-Markovianty of open quantum systems.However,it is worth noting that the measure is effective only for any unital map Φ()=,i.e.,the phase damping channel and random unitary channel.As for the nonunital map Φ()/=,i.e.,the amplitude damping channel,the measure may be invalid,which is agreement with the assertion of Ref.[43],namely it has been revealed that the nonunitality is a necessary condition for the increase of the purity Trρ2under quantum channels.In other words,the non-unital map may increase the purity of quantum system.

Before defining the measure of non-Markovianity based on the BZ invariant informationIBZ(ρ), first let us recall that if a quantum dynamical map{Φt}is called Markovian process in the sense of divisibility,[14]there will be that

where Φt,τis the map of any middle quantum process.The relation Eq.(3)holds true for all time-dependent Markovian quantum processes including the canonical time independent Lindblad generators(which satisfies a dynamical semigroup property)and time-dependent generators(which satisfies a dynamical divisibility property).

For the system’s density operator at any timetwithρ(t)= Φtρ(0),the BZ invariant informationIBZ(ρ)exists the following inequality relation as

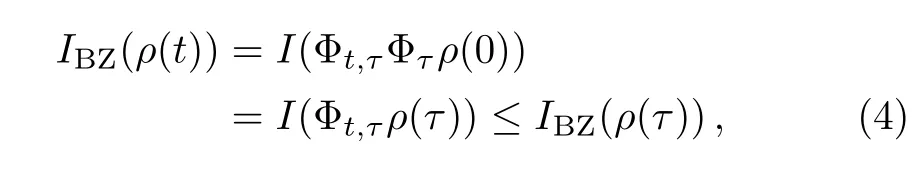
where the contractivity of theIBZ(ρ)under any completely positive and trace preserving bistochastic(or unital)maps has been used as the property(b)of theIBZ(ρ),i.e.,IBZ(Φρ)≤IBZ(ρ). Clearly,Eq.(4)means that theIBZ(ρ(t))is a monotonically decreasing function of time for any Markovian process of system,namely(d/dt)IBZ(ρ(t))≤0.On the contrary,the violation of this monotonicity of theIBZ(ρ(t)),namely(d/dt)IBZ(ρ(t))＞0,can be used as an indicator for non-Markovian process of system.Thus we may define a measure via theIBZ(ρ(t))for non-Markovianity of system by

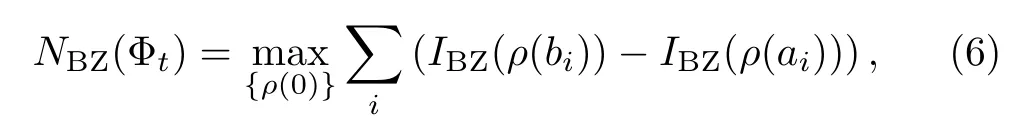
where the sup is over all initial statesρ(0)on system.The non-Markovianity measure in Eq.(5)can be rewritten as wherebiandaicorrespond to the time points of the local maximum and minimum ofIBZ(ρ(t)),respectively.Obviously,the measures as in Eqs.(5)and(6)involve the formidable optimization problem,which generally is complicated for calculations.However,theIBZ(ρ(t))of the proposed measure only involves the purity of the quantum stateρ(t),which is very simple to compute.Especially,in the following we will show that the maximization in the proposed measure can be actually removed for the considered models without influencing the sensibility of measure to detect non-Markovianity.

3 Applications to a Qubit Open Systems

3.1 Non-Markovianity of a Phase Damping Channel

First we consider a model of a qubit system undergoing non-Markovian phase damping channel,which is governed by the following equation[44]

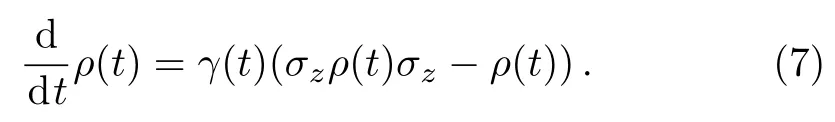
For any initial states of qubit withthe density operator of the qubit at any timetcan be given by

Accordingly,the derivatives of theIBZ(ρ(t))can be easily given by

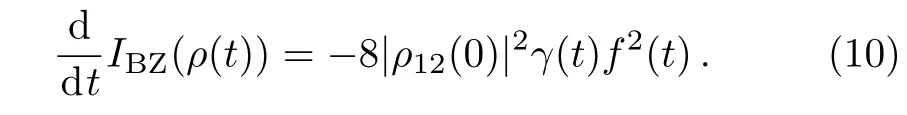
Therefore,the dynamics of system exhibits a Markovian process if and only ifγ(t)≥0 for allt≥0.Once the conditionγ(t)＜0 for some timet,the dynamics of system shows a non-Markovian process.This result is in accordance with that of information flow,[28]divisibility[28]and quantum mutual information.[22]

Finally,we obtain the explicit expression of the non-Markovianity measureNBZ(Φt)as

Obviously,the maximum in Eq.(11)is achieved with equatorial,antipodal states[45−46]i.e.,ρ(0)=|±〉〈±|withActually,the maximization can be removed due to the intervals in which non-Markovianity occurs are uniquely determined by the conditionγ(t)＜0,which does not affect the sensibility ofNBZ(Φt)to detect non-Markovianity.Of course,the choice of initial states can influence the amount of non-Markovianity.Now,theNBZ(Φt)can be simplified as

As a concrete example,using non-Markovianity measure Eq.(12)we discuss the non-Markovianity of an exact solved model consisting of a qubit interacting with a thermal environment by the dephasing mechanism,where thewith the time-dependent dephasing rateγ(t)with the dephasing rate at zero temperature case of the environment given by

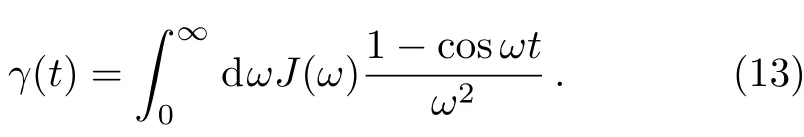
In what follows,we assume the spectral density of the environment is Ohmic-like form[44,47−48]

whereωcis the environment cutoff frequency.By changing thesparameter one goes from sub-Ohmic environments(s＜1)to Ohmic(s=1)and super-Ohmic(s＞1)environments,respectively.Now the dephasing rate as Eq.(13)exists an explicit expression as[49]

which leads to an exact form of thef(t)asf(t)=exp[−2∫t0γ(τ)dτ]=exp[−β(t)]with[50]where Γ[x]is the Euler gamma function.Having Eq.(16)in hand,we plot the non-MarkovianityNBZ(Φt)as a function of the ohmicity parametersin Fig.1.

Fig.1 (Color online)The non-Markovianity NBZ(Φt)as a function of the ohmicity parameter s.

From Fig.1,we can clearly see that when the ohmicity parameters＞scrit=2 the non-MarkovianityNBZ(Φt)is always nonzero.Especially,fors＞4 theNBZ(Φt)also exist,and only take very small values.This result agrees with the main result of Refs.[49–50]based on information flow in the same model,where using the convexity arguments it is shown that non-Markovian or memory effects leading to information flow and recoherence occur only if the reservoir spectrum is super-Ohmic withs＞2.Moreover,the non-MarkovianityNBZ(Φt)shows a nonmonotonic behavior with increase of thesand the maximal non-Markovianity can be achieved at a specified values.Finally,compared with the popular non-Markovianity measure( first proposed by Breuer,Laine,and Piilo(BLP)in Ref.[8])based on information flow,we find that the amount of non-MarkovianityNBZ(Φt)have a subtle difference.The difference can be explained by taking into account the expression of non∫-Markovianity of the BLP measure withNBLP(Φt)=−2γ(t)＜0γ(t)f(t)dt[28]for the same phase damping model,which is different from Eq.(12)of proposed non-Markovianity measure.

3.2 Non-Markovianity of Random Unitary Channel

Then we consider a model of a qubit(considered subsystemS)suffering from random unitary channel,which is governed by the master equation[30−31]

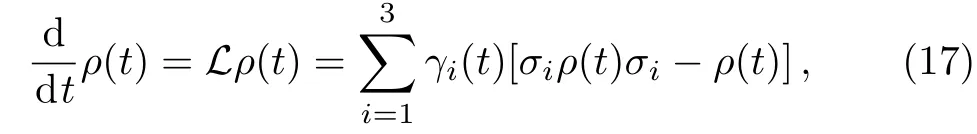
whereγi(t),σi(i=1,2,3)represent time-dependent decay factors and the Pauli matrices,respectively.Obviously,the so-called random unitary channel as Eq.(17)is a generalization of Eq.(7)by introducing two additional decoherence channels.The corresponding random unitary dynamical map[31]can be given by

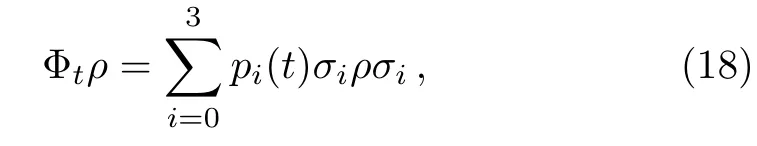
whereσ0=1,pi(t)≥0,andEspecially,att=0 the Φ0=impliesp0(0)=1 andpi(0)=0(i=1,2,3).The relationships betweenpi(t)andγi(t)are associated with an additional parameterλi(t),namely[31]

i

0ii(i=0,1,2,3)satisfies the equation

For the initial states of a qubit with the Bloch-sphere form

in view of Eq.(20)the density operator at any timet ρ(t)= Φtρ(0)can be obtaine(das)

whereh(t)=e−2[Γ1(t)+Γ2(t)],w(t)=e−2Γ3(t)[ae2Γ1(t)−ibe2Γ2(t)],aandbdenote the real and imaginary part ofw,respectively.Obviously,the unital relation Φ()=is satisfied for the random unitary channel.As an upshot,the explicit expression of theIBZ(ρ(t))can be easily represented as

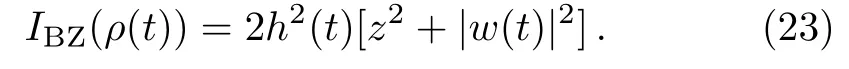
Correspondingly,the derivatives of theIBZ(ρ(t))can be easily given by

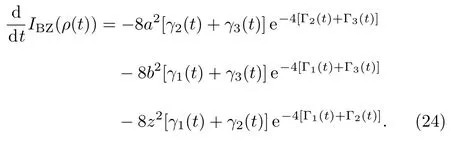
Similar to the case of phase damping channel,the dynamics of system indicates a Markovian process,i.e.,(d/dt)IBZ(ρ(t))≤0 if and only if

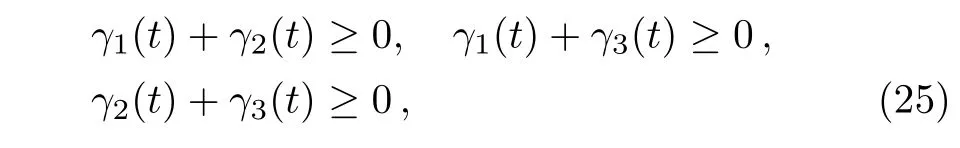
for allt≥0. Interestingly,these Markovian conditions are in accordance with that of information flow[31]and von Neumann entropy,[31,51]but are different from divisibility[31]and quantum mutual information.[32]For the random unitary channel,[31−32]it has been indicated that the the conditions of three non-Markovianity measures including information flow,divisibility and quantum mutual information are not equivalent each other.Actually,at present for multichannel model various non-Markovianity measures are not unified and even controversial in quantifying non-Markovian behavior of quantum processes.And each of them has some own advantages,such as information flow has a good operational interpretation in view of information exchange between the system and the environment.Moreover,clearly whenγ1(t)=γ2(t)=0,the random unitary channel reduces to the phase damping channel.Correspondingly,the condition of Markovian process of system reduces toγ3(t)≥0,which just is the condition of phase damping channel with Markovian dynamics as given in the above section.

4 Conclusions

We proposed an alternative non-Markovianity measure based on BZ invariant information for unital quantum dynamical maps.The main advantage of the proposed non-Markovianity measure is the simplicity of its calculations.Further,we applied the non-Markovianity measure to two typical noise channels including phase damping channel and random unitary channel(which possesses unital characterization)and found that the non-Markovian conditions of the phase damping channel is the same to other non-Markovianity measures,i.e.,information flow,divisibility and quantum mutual information,but for the random unitary channel the relation among proposed non-Markovianity measure and other non-Markovianity measures about the non-Markovian conditions is complex.Concretely,we obtained that the non-Markovian conditions are consistent with the measure based on information flow,but is different from other measures,i.e.,divisibility and quantum mutual information.Up to now,for the random unitary channel the conditions of various non-Markovianity measures are not unified and even debatable,which deserves further investigation.In a word,the proposed non-Markovianity measure in the paper may be potential applications in investigating non-Markovian dynamics of open quantum systems.More recently,we noted that Intravaiaet al.[52]investigated non-Markovianity in atom-surface dispersion forces and found that the Markov approximation can lead to erroneous predictions of such phenomena with regard to both strength and functional dependencies on system parameters,which further highlights the importance of non-Markovian effects in dispersion interactions.

[1]A.Rivas,S.F.Huelga,and M.B.Plenio,Rep.Prog.Phys.77(2014)094001.

[2]H.P.Breuer,E.M.Laine,J.Piilo,and B.Vacchini,Rev.Mod.Phys.88(2016)021002.

[3]B.H.Liu,L.Li,Y.F.Huang,et al.,Nat.Phys.7(2011)931.

[4]J.S.Tang,C.F.Li,Y.L.Li,et al.,Europhys.Lett.97(2012)10002.

[5]F.F.Fanchini,G.Karpat,B.Akmak,et al.,Phys.Rev.Lett.112(2014)210402.

[6]B.H.Liu,S.Wißmann,X.M.Hu,et al.,Sci.Rep.4(2014)6327.

[7]N.K.Bernardes,A.Cuevas,A.Orieux,et al.,Sci.Rep.5(2015)17520.

[8]H.P.Breuer,E.M.Laine,and J.Piilo,Phys.Rev.Lett.103(2009)210401;H.P.Breuer,J.Phys.B:At.Mol.Opt.Phys.45(2012)154001.

[9]A.K.Rajagopal,A.R.Usha Devi,and R.W.Rendell,Phys.Rev.A 82(2010)042107.

[10]X.M.Lu,X.G.Wang,and C.P.Sun,Phys.Rev.A 82(2010)042103.

[11]H.Song,S.Luo,and Y.Hong,Phys.Rev.A 91(2015)042110.

[12]S.Lorenzo,F.Plastina,and M.Paternostro,Phys.Rev.A 88(2013)020102.

[13]B.Bylicka,D.Chruscinski,and S.Maniscalco,Sci.Rep.4(2014)5720.

[14]M.M.Wolf,J.Eisert,T.S.Cubitt,and J.I.Cirac,Phys.Rev.Lett.101(2008)150402.

[15]A.Rivas,S.F.Huelga,and M.B.Plenio,Phys.Rev.Lett.105(2010)050403.

[16]D.Chrušciński,A.Kossakowski,and A.Rivas,Phys.Rev.A 83(2011)052128.

[17]S.C.Hou,X.X.Yi,S.X.Yu,and C.H.Oh,Phys.Rev.A 83(2011)062115;S.C.Hou,S.L.Liang,and X.X.Yi,Phys.Rev.A 91(2011)012109.

[18]D.Chrušciński and S.Maniscalco,Phys.Rev.Lett.112(2014)120404.

[19]Z.Y.Gao,Y.K.Ren,and H.S.Zeng,Quant.Inf.Process.15(2016)3043.

[20]Z.L.Fan,Y.K.Ren,and H.S.Zeng,Chin.Phys.B 25(2016)010303.

[21]S.Alipour,A.Mani,and A.T.Rezakhani,Phys.Rev.A 85(2012)052108.

[22]S.Luo,S.Fu,and H.Song,Phys.Rev.A 86(2012)044101.

[23]Z.He,C.Yao,Q.Wang,and J.Zou,Phys.Rev.A 90(2014)042101.

[24]H.S.Dhar,M.N.Bera,and G.Adesso,Phys.Rev.A 91(2015)032115.

[25]F.M.Paula,P.C.Obando,and M.S.Sarandy,Phys.Rev.A 93(2015)042337.

[26]G.Guarnieri,A.Smirne,and B.Vacchini,Phys.Rev.A 90(2014)022110.

[27]M.M.Ali,P.Y.Lo,M.W.Y.Tu,and W.M.Zhang,Phys.Rev.A 92(2015)062306.

[28]H.S.Zeng,N.Tang,Y.P.Zheng,and G.Y.Wang,Phys.Rev.A 84(2011)032118.

[29]P.Haikka,J.D.Cresser,and S.Maniscalco,Phys.Rev.A 83(2011)012112.

[30]B.Vacchini,J.Phys.B:At.Mol.Opt.Phys.45(2012)154007.

[31]D.Chrušciński and F.Wudarski,Phys.Lett.A 377(2013)1425.

[32]M.Jiang and S.Luo,Phys.Rev.A 88(2013)034101.

[33]D.Chrušciński and F.Wudarski,Phys.Rev.A 91(2015)012104.

[34]C.Brukner and A.Zeilinger,Phys.Rev.Lett.83(1999)3354.

[35]J.Lee and M.S.Kim,Phys.Rev.Lett.84(2000)4236.

[36]J.Rehacek and M.S.Kim,Phys.Rev.Lett.88(2002)130401.

[37]S.Luo,Theor.Math.Phys.151(2007)693.

[38]A.E.Rastegin,Proc.R.Soc.A 471(2015)20150435.

[39]J.Lee,M.S.Kim,and Z.Hradil,Phys.Rev.Lett.91(2003)087902.

[40]M.Ozawa,Phys.Lett.A 268(2000)158.

[41]M.A.Nielsen and I.L.Chuang,Quantum Computation and Quantum Information,Cambridge University Press,Cambridge(2000).

[42]I.Bengtsson and K.Zyczkowski,Geometry of Quantum States:An Introduction to Quanutm Entanglement,Cambridge University Press,Cambridge(2006).

[43]D.A.Lidar,A.Shabini,and R.Alicki,Chem.Phys.322(2006)82.

[44]H.P.Breuer and F.Petruccione,The Theory of Open Quantum Systems,Oxford University Press,Oxford(2002).

[45]Z.Y.Xu,W.L.Yang,and M.Feng,Phys.Rev.A 81(2010)044105.

[46]Z.He,J.Zou,L.Li,and B.Shao,Phys.Rev.A 83(2011)012108.

[47]A.J.Leggett,S.Chakravarty,A.T.Dorsey,M.P.A.Fisher,A.Garg,and W.Zwerger,Rev.Mod.Phys.59(1987)1.

[48]G.M.Palma,K.Suominen,and A.Ekert,Proc.R.Soc.London A 452(1996)567.

[49]P.Haikka,T.H.Johnson,and S.Maniscalco,Phys.Rev.A 87(2013)010103.

[50]C.Addis,B.Bylicka,D.Chrušciński,and S.Maniscalco,Phys.Rev.A 90(2014)052103.

[51]S.Hasenli,S.Salimi,and A.S.Khorashad,Quant.Inf.Process.14(2015)3581.

[52]F.Intravaia,R.O.Behunin,C.Henkel,K.Busch,and D.A.R.Dalvit,Phys.Rev.A 94(2016)042114.