Investigation of Conformable Fractional Schrödinger Equation in Presence of Killingbeck and Hyperbolic Potentials∗

Won Sang Chung,Soroush Zare,and Hassan Hassanabadi

1Department of Physics and Research Institute of Natural Science,College of Natural Science,Gyeongsang National University,Jinju 660-701,Korea

2Department of Basic Sciences,Islamic Azad University,North Tehran Branch,Tehran,Iran 3Physics Department,Shahrood University of Technology,Shahrood,Iran

1 Introduction

Idea of using fractional form of Schrödinger equation,has been one the most novel and fundamental idea.This topic was introduced first by Laskin in the path integral of the Lévy trajectories.[1−4]This form of Schrödinger equation can be written as

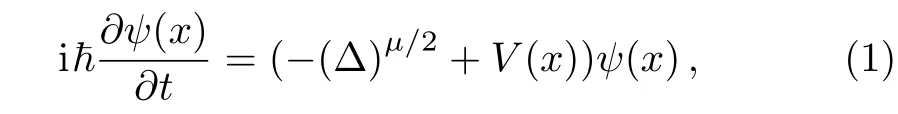
where 0＜µ≤2.So ifα=2,the ordinary Laplacian operator will be recovered.[5−6]Such formalism of quantum mechanics has an elegant applications in mathematics and physics.For example,if we want to express complicated behavior of disordered system,we have to use Lévy flights[7−9]in which concentration state of particles performing Lévy flights satisfies in its simplest form a diffusion equation where the Laplacian operator is replaced by a fractional derivative,indeed Lévy flights are relevant to many physical,[10−14]chemical,biological[15−17]and socio-economic[18−20]systems.Another applications of fractional calculus can be found in nonlinear oscillation of earthquake,[21]fluid-dynamic traffic model with fractional derivatives,[22]seepage flow in porous media[23]and differential equations with fractional order to the modeling of many physical phenomena.[23]Among lots of great and remarkable articles in fractional calculus literature we are going to mention to some of them to end this part.Kirichenkoet al.,studied Lévy flights with arbitrary index 0＜µ≤2 inside a potential well of in finite depth.[24]Kazem,applied the Laplace transform for solving linear fractional-order differential equation.[25]Mainardi has done a review of some applications of fractional derivatives in continuum and statistical mechanics.[26]

In what follows,we organized this article as follows:Section 2 contains preliminary round fractional form of Schrödinger equation.Section 3 consists of two subsections that in the first subsection Killingbeck potential for fractional formalism os Schrödinger equation has been studied and in the next subsection the thing has been done for hyperbolic potential.

2 Conformable Fractional Form of Schrödinger Equation

For a smooth function inx,µ(x),theµ(x)deformed derivative(shortlyµ-derivative)is defined by

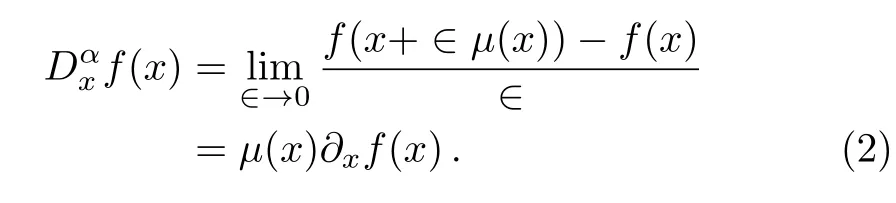
Theµ(ˆx)-deformed(or conformable fractional)quantum mechanics has the following postulates:

In theµ(ˆx)-deformed quantum mechanics,the time dependent Schrödinger equation reads

where the coordinate realization ofˆx,ˆpare

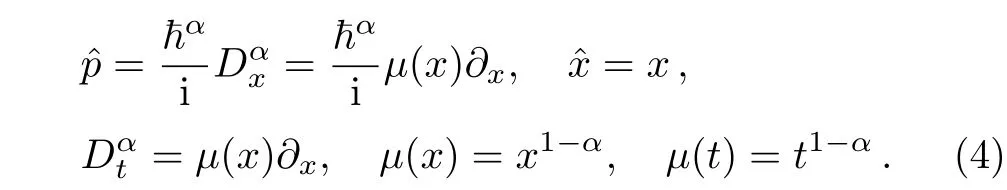
Here we callDαxaµ-deformed derivative.Whenµ(x)reduces to 1,Eq.(3)gives an ordinary quantum mechanics.Andψ(x,t)describes a physical state.In theµ-deformed quantum mechanics,the commutation of the position operatorˆxand momentum operatorˆpis

The coordinate realizations of the position operator and momentum operator are

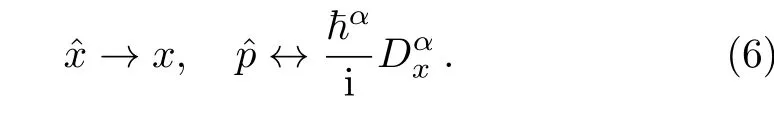
Then,the Schrödinger equation reads

If we setψ(x,t)=exp{−(i/ħ)Eα(tα/α)}U(x),we have the time-independent Schrödinger equation as follows;

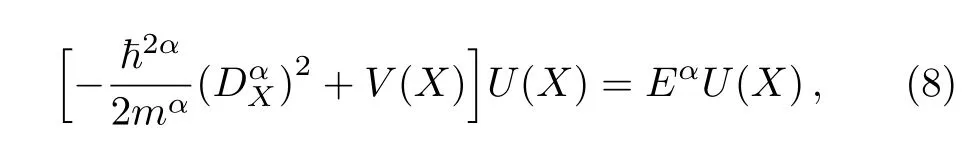
where

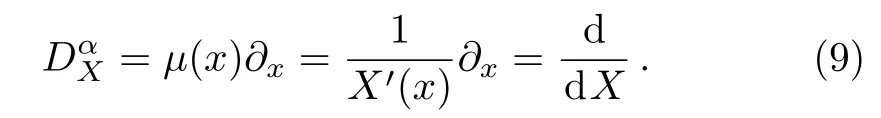
Therefore

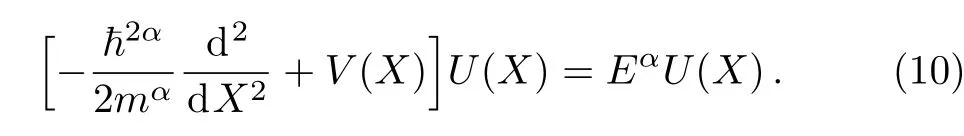
3 Interactions

Now we are in a position that we should consider some physical interactions for considered formalism.First we set Killingbeck potential after that a hyperbolic interaction,will be studied.

3.1 Killingbeck Potential

By considering Killingbeck Potential as follows and substituting it into Eq.(9),we have[27]

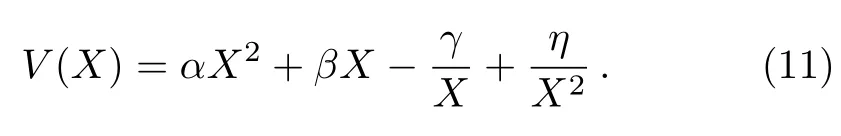
Thus by substitution new ansatz function

into Eq.(10).We will have

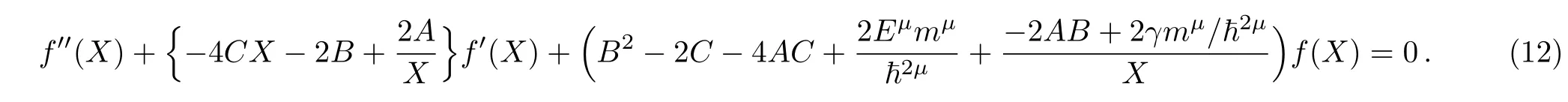
On the other hand by getting changing variableinto above equation can be written as:

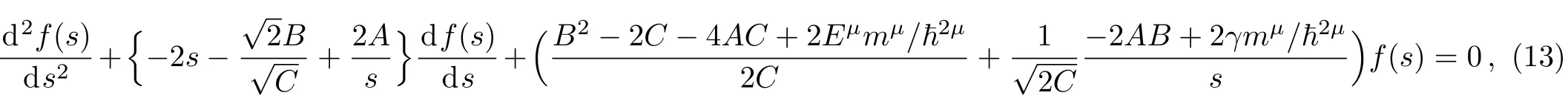
where

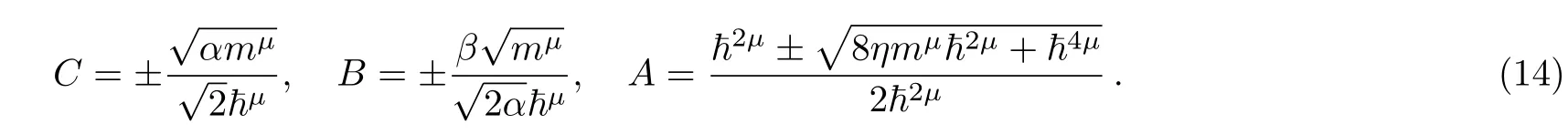
For a suitable boundary condition

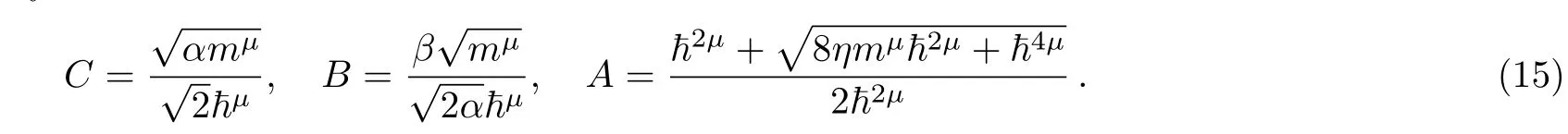
On the other hand the biconfluent Heun equation is as

By comparing Eqs.(11)and(14)

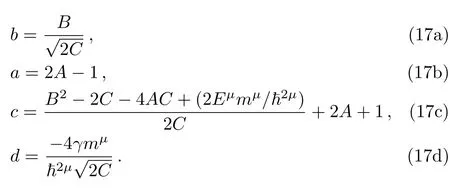
Let us present solution of Eq.(13)

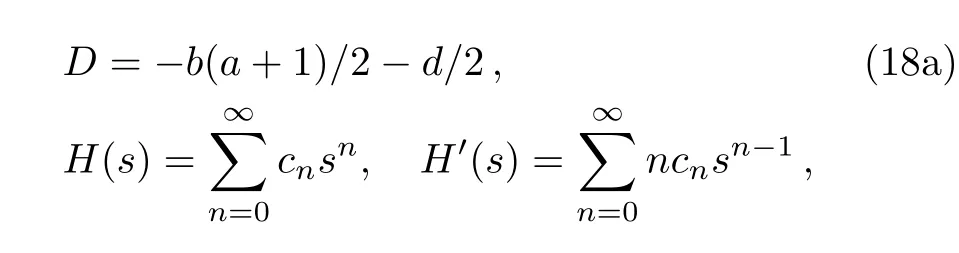
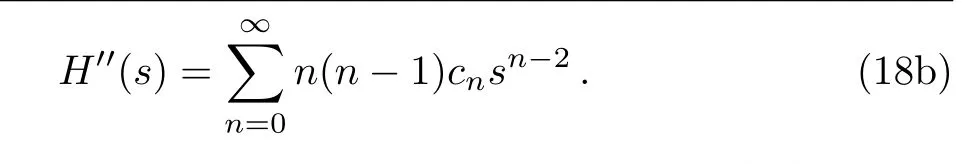
On the other hand by attention to Eq.(16)can be written as:

Thus we arrive at the recurrent relations for series coefficients

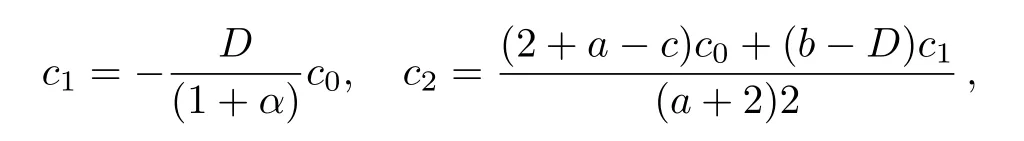
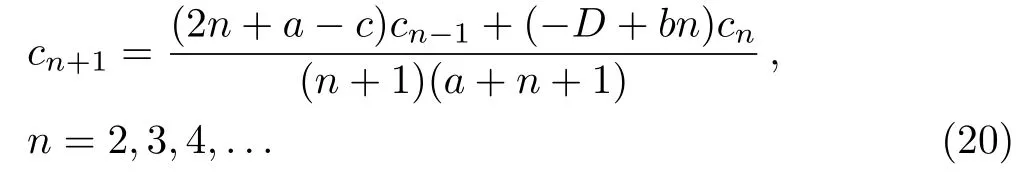
Therefore wave function as following form:

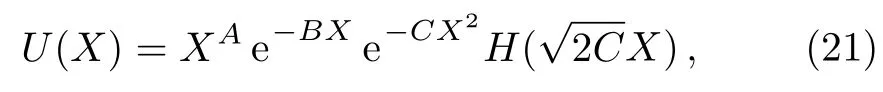
where

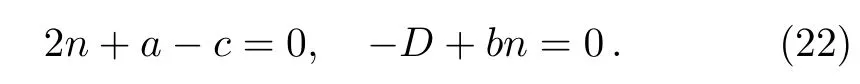
3.2 Hyperbolic Potential

Consider the following class of potentials,defined by two physical parametersV0andδ,shaping the potential depth and width respectively,and with two class parameters,withq=−2,0,2,4,6 defining the family andp=−2,0,...,q

Therefore we consider the hyperbolic double well potential under consideration above equation with[28]

therefore potential into Eq.(25)as the following form:

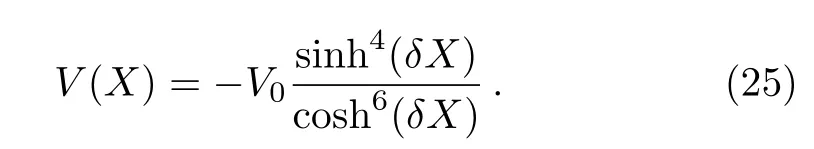
To have an understanding of considered potential,Eq.(25)is depicted as

Thus by substituting Eq.(24)into Eq.(10).We will have

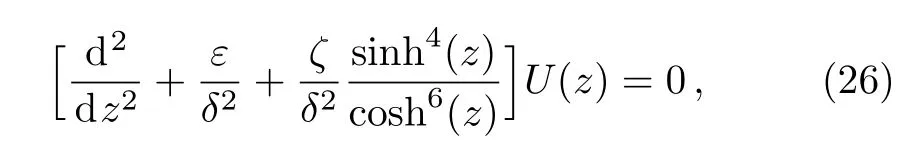
Whereε=2mαEα/ħ2α,ζ=2mαV0/ħ2α,andδX=z.Upon making the change of variables=sech2zsuch that the domain−∞＜X＜∞maps to 0＜s＜1,we find

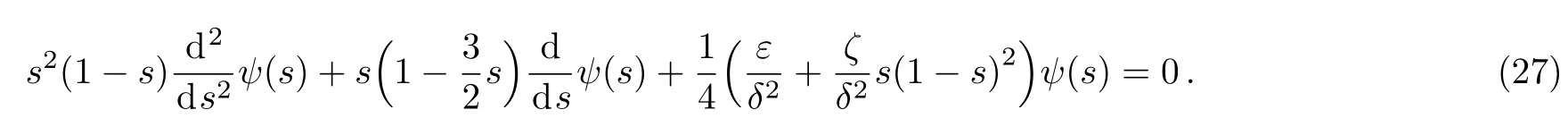
Let us to choose the ansatz solutionψ(s)=e(ω/2)sf(s)which yields upon substitution into Eq.(27)

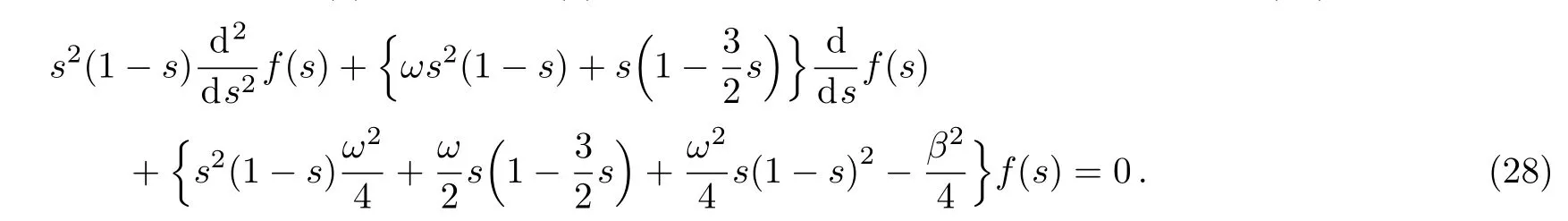
Withf(s)=sβ/2y(s)we find

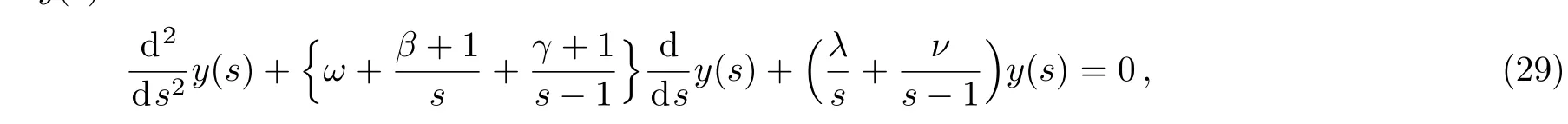
where

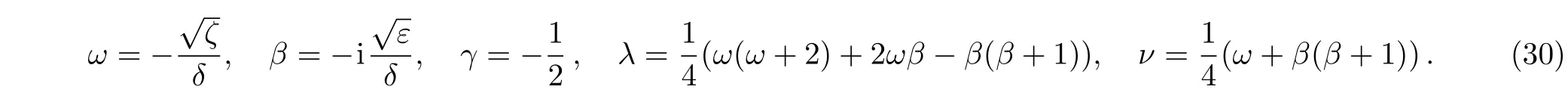
This is Heuns confluent differential equation.It has as a solution around the regular singular points=0 given by the confluent Heun function.[29−31]

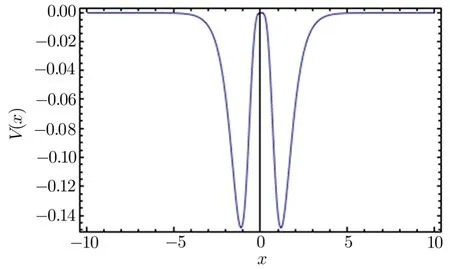
Fig.1 Plot of the hyperbolic double-well potential under consideration,Eq.(23)with(p,q)=(6,4).

Finally Eq.(28)as the following form

for processing further

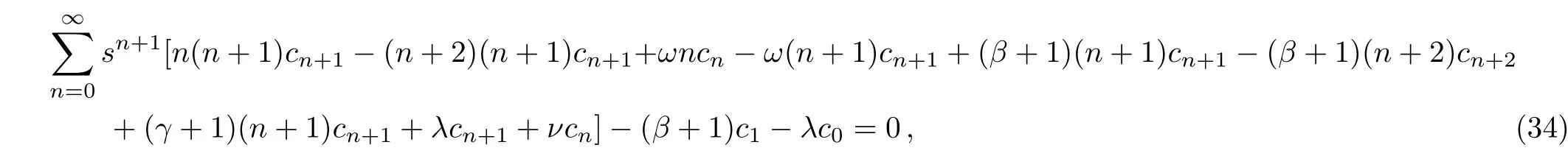
where

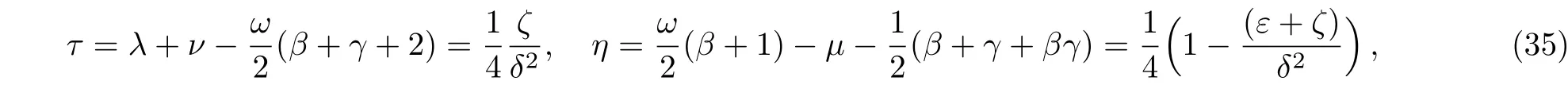
and the coefficientscnare given by the three-term recurrence relation

By transformedn⇒n−2,we will have

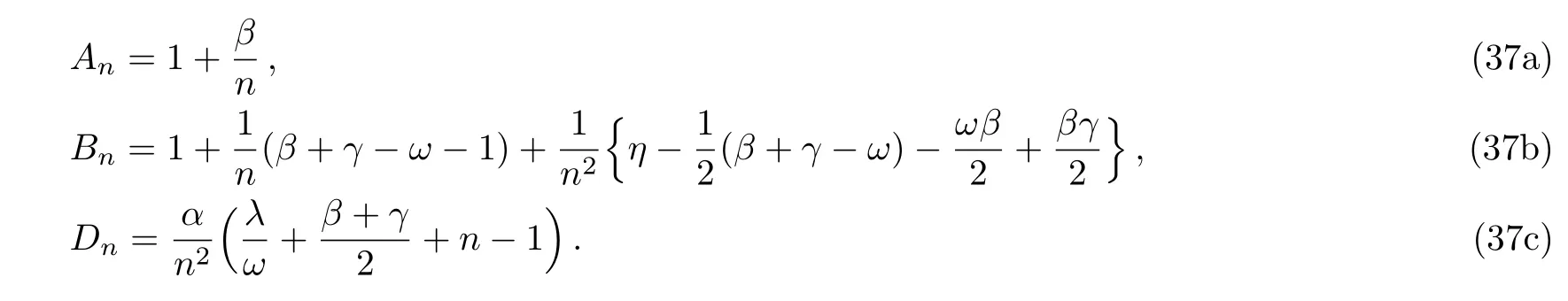
Thus we have found the following solution to the Schrödinger Eq.(25)

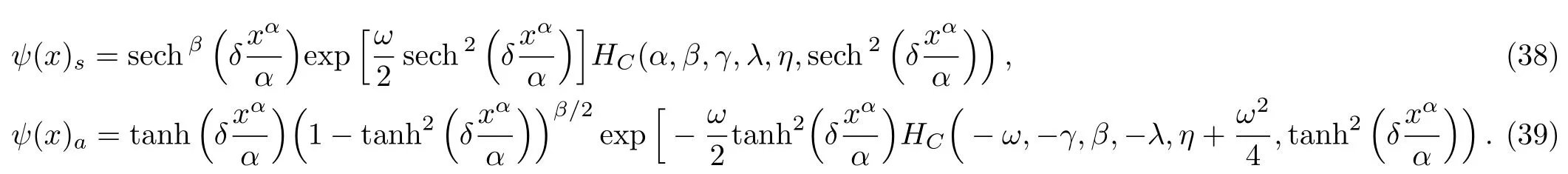
4 Conclusion

In this study,after presenting conformable fractional form of Schrödinger equation,we considered two different potentials as interactions of system.In the first case,Killingbeck potential was studied and for the next case hyperbolic potential.In order to obtain wave functions and energy eigen values,we took some ansatz that functions which caused to find the wave function with the aim of biconfluent and confluent Heun functions respectively.Using series expansions energy eigen values were obtained as well.

Acknowledgment

The authors would like to thank the kind referee for his/her meticulous critics and comments.

[1]N.Laskin,Phys.Lett.A 268(2000)298.

[2]N.Laskin,Phys.Rev.E 62(2000)3135.

[3]N.Laskin,Chaos 10(2000)780.

[4]N.Laskin,Phys.Rev.E 66(2002)056108.

[5]I.Podlubny,Fractional Differential Equations,Academic Press,London(1999).

[6]S.G.Samko,A.A.Kilbas,and O.I.Maritchev,Fractional Integrals and Derivatives,Gordon and Breach,New York(2003).

[7]Lévy Flights and Related Topics in Physics,ed.by M.F.Shlesinger,G.M.Zaslavsky,and U.Frisch,Lecture Notes in Physics,Springer-Verlag,Berlin(1995).

[8]B.D.Hughes,Random Walks,and Random Environments,Vol.1,Clarendon Press,Oxford(1995).

[9]Chaos:The InterplayBetweenDeterministicand Stochastic Behavior,ed.by P.Garbaczewski,M.Wolf,and A.Weron,Springer-Verlag,Berlin(1995).

[10]G.M.Zaslavsky,Hamiltonian Chaos and Fractional Dynamics,Oxford University Press,New York(2005.)

[11]D.del-Castillo-Negrete,B.A.Carreras,and V.E.Lynch Cole,Phys.Rev.Lett.91(2003)018302.

[12]B.Bergersen and Z.Racz,Phys.Rev.Lett.67(1991)3047.

[13]S.Schaufler,W.P.Schleich,and V.P.Yakovlev,Phys.Rev.Lett.83(1999)3162.

[14]A.Carati and L.Galgani,Phys.Rev.Lett.90(2003)010601.

[15]G.M.Viswanathan,V.Afanasyev,S.V.Buldyrev,et al.,Nature(London)381(1996)413.

[16]E.N.Govorun,V.A.Ivanov,A.R.Khokhlov,et al.,Phys.Rev.E 64(2001)040903.

[17]N.Scafetta,V.Latora,and P.Grigolini,Phys.Rev.E 66(2002)031906.

[18]R.N.Mantegna and H.E.Stanley,An Introduction to Econophysics,Correlations and Complexity in Finance,Cambridge University Press,Cambridge(2000).

[19]W.Schoutens,Lévy Processes in Finance,Wiley Finance,New York(2003).

[20]S.Rachev,Y.Kim,M.Bianchi,and F.Fabozzi,Financial Models with Lévy Processes and Volatility Clustering,Wiley,New York(2011).

[21]J.H.He,Nonlinear Oscillation with Fractional Derivative and Its Applications,inProceedings of the Inter-national Conference on Vibrating Engineering,Dalian,China(1998)288–291.

[22]J.He,Bull.Sci.Technol.15(1999)86.

[23]J.He,Comput.Methods.Appl.Mech.Eng.167(1998)57.

[24]E.V. Kirichenko, Piotr Garbaczewski, Vladimir Stephanovich,and Mariusz Zaba,Phys.Rev.E 93(2016)052110.

[25]Saeed Kazem,Int.J.Nonlinear Science 16(2013)3.

[26]F.Mainardi,Fractional Calculus:Some Basic Problems in Continuum and Statistical Mechanics,Fractals and Fractional Calculus in Continuum mechanics,Springer-Verlag,New York(1997)291.

[27]E. Ovsiyuk, O. Veko, and M. Amirfachrian,arXiv:1110.5121v1,24 Oct.(2011).

[28]C.A.Downing,J.Math.Phys.54(2013)072101.

[29]S.S.Dong,G.H.Sun,B.J.Falaye,and S.H.Dong,Eur.Phys.J.Plus 131(2016)176.

[30]S.S.Dong,Q.Fang,B.J.Falaye,et al.,Mod.Phys.Lett.A 31(2016)1650017.

[31]G.H.Sun,S.H.Dong,K.D.Launey,T.Dytrych,and J.P.Draayer,Int.J.Quant.Chem.115(2015)891.