New Stability Criteria for High-Order Neural Networks with Proportional Delays∗

Chang-Jin Xu(徐昌进) and Pei-Luan Li(李培峦)2Guizhou Key Laboratory of Economics System Simulation,Guizhou University of Finance and Economics,Guiyang 550004,China

2School of Mathematics and Statistics,Henan University of Science and Technology,Luoyang 471023,China

1 Introduction

It is well known that considerable attention has been paid to high-order neural networks as well as various generalizations for their immense applications in many fields such as pattern recognition,optimization and image processing and so on.[1−15]On the one hand,the existence and stability of the equilibrium point of cellular neural networks plays an important role in practical application.On the other hand,time delay is inevitable due to the finite switching speed of information processing and the inherent communication time of neurons,moreover,its existence may cause the instability of networks.[16]Thus many interesting stability results on high-order neural networks with delays have been available.[17−21]At present,the time delays considered for high-order neural networks can be classified as constant delays,[2,17,19,22−23]time varying delays,[6,24−25]and distributed delays.[26−28]Here we would like to point out that the proportional delay which is a special delay type exists in some fields such as physics,biology systems,control theory,and Web quality of service(QoS)routing decision.Since the presence of an amount of parallel pathways of a variety of axon sizes and lengths,a neural network usually has a spatial structure,it is reasonable to introduce the proportional delays into the neural network.In an amount of parallel pathways,affected by different materials and topology,there may be some unbounded delays that is proportional to the time,thus we should choose suitable proportional delays factors in view of different cases and adopt proportional delays to characterize these unbounded delays.[29]Recently,there are only very few papers that focus on this aspect.For example,Zhou[30]considered the global asymptotic stability of cellular neural networks with proportional delays,Zhou[31]studied the delay-dependent exponential stability of cellular neural networks with multiproportional delays,Zhou[32]investigated the dissipativity of a class of cellular neural networks with proportional delays,Zhouet al.[9]analyzed the asymptotic stability of cellular neural networks with multiple proportional delays,Zhenget al.[33]established the stability criteria for highorder networks with proportional delay,Zhou[34]discussed the delay-dependent exponential synchronization of recurrent neural works with multiple proportional delays.We must point out that neural networks with proportional delays have been widely applied in many fields such as light absorption in the star substance and nonlinear dynamic systems.Therefore the study on the high-order neural networks with proportional delays has important theoretical and practical value.

In 2015,Zhenget al.[33]investigated thep-th exponential stability of the following high-order neural networks with proportional delays

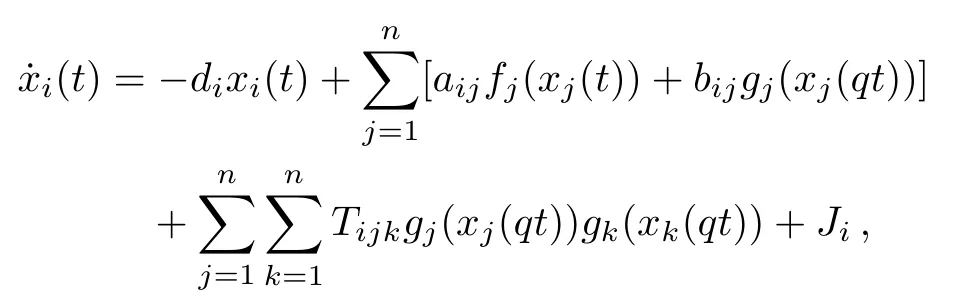
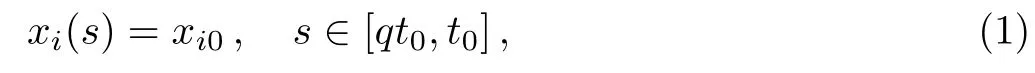
wherei=1,2,...,n,xi(t)stands for the membrane potential potential of thei-th neuron at the timet,di＞0 is a constant,fj(.),gj(.):R→R represent the nonlinear activation functions,aijandbijrepresent the synaptic connection weights between thej-th neuron and thei-th neuron at timet,qt,respectively.Tijkis the secondorder synaptic weights of the neural networks,Jiis the external input,qis the proportional delay factor and satisfies 0＜q＜1,qt=t−(1−q)t,in which(1−q)tdenotes the transmission delay and is the unbounded delay.By applying Lyapunov method,matrix measure and generalized Halanay inequality,Zhou and Zhenget al.[33]obtained some stability criteria to ensure thep-th exponential stability of system(1).Different from the work of Ref.[33],in this paper,we will investigate the exponential stability of the following more generalized version of system(1)by a new method based on constructing the delay differential inequality

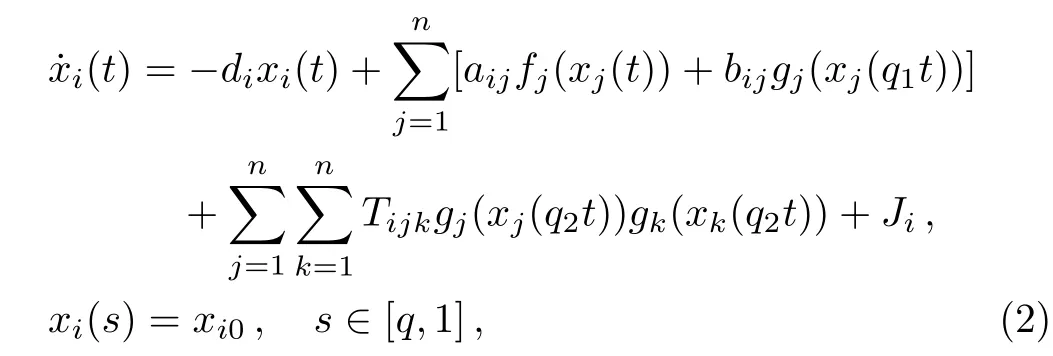
where 0＜q1,q2＜1,q1t=t−(1−q1)t,q2t=t−(1−q2)t,in which(1−q1)tand(1−q2)tdenote the transmission delays and are the unbounded delays,q=min{q1,q2}andx(0)=(x10,x20,...,xn0)T.In many cases,the transmission of signal has different time delays.Thus it is more reasonable to introduce different proportional delay factors in model(2).The results of this paper are completely new and complement those of the previous studies in Ref.[33].The approach is new.

Throughout this paper,we make the following assumptions:

(H)Fori=1,2,...,n,there exist positive constantsLiandGisuch that|fi(u)−fi(v)|≤Li|u−v|,|gi(u)−gi(v)|≤Gi|u−v|,|fi(u)|≤ ϱi,|gi(u)|≤σifor allu,v∈R.

The organization of the rest of this paper is as follows.In Sec.2,some preliminaries are presented and some sufficient conditions are derived for the existence,uniqueness and global exponential stability of the equilibrium point of Eq.(2)by constructing the delay differential inequality.In Sec.3,we present two examples to illustrate the feasibility and effectiveness of our main theoretical findings in previous sections.A brief conclusion is drawn in Sec.4.

2 Main Results

In this section,we consider the global exponential stability of system(3)by constructing the delay differential inequality.

Consider the transformation defined by

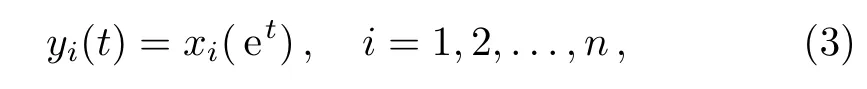
Then Eq.(2)can be rewritten as

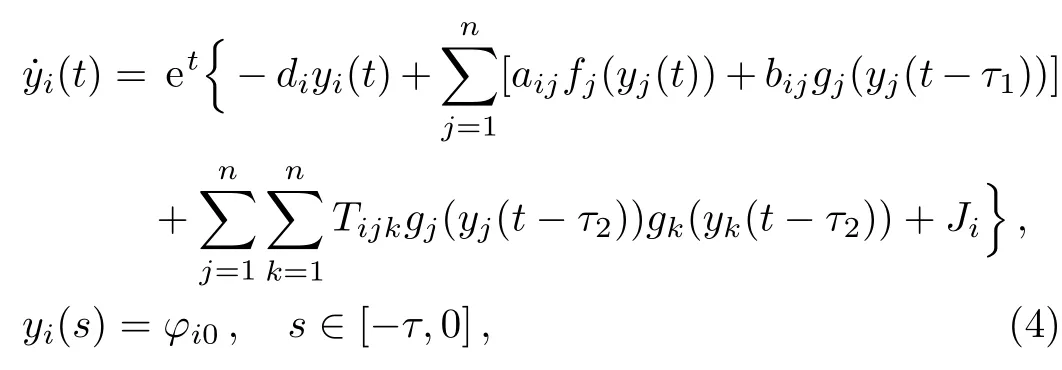
wherei=1,2,...,n,t＞0,τ1=−logq1,τ2=−logq2,τ=max{τ1,τ2},φ=(φ1,φ2,...,φn)T,in whichφi=

xi0.

Definition 1An equilibrium pointy∗=(y∗1,y∗2,...,y∗n)Tof the system(4)is said to bep-th(p=1,2,∞)globally exponentially stable,if there exist two positive constantsλ≥1 andη＞0 such that

i

n whichηis said to be globally exponentially convergent rate.

Lety(t)be an arbitrary solution of system(4)fort＞0,wherey(t)=(y1(t,φ),y2(t,φ),...,yn(t,φ))TLet

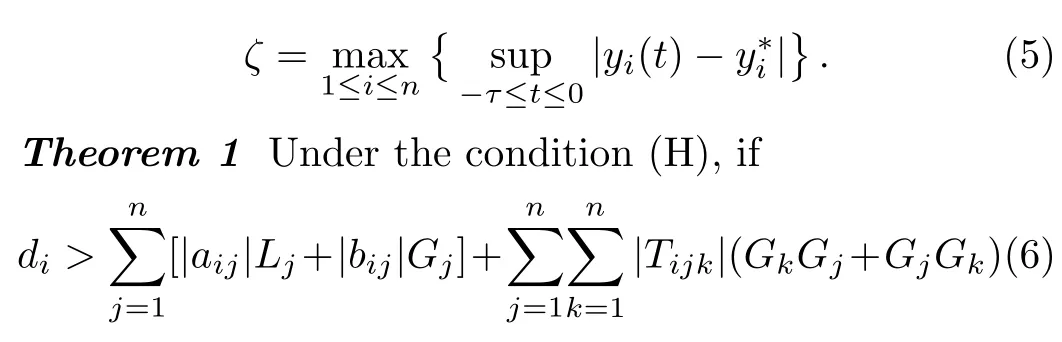
holds for alli=1,2,...,n,then system(2)has a unique equilibriumx∗,which is globally exponentially stable.

ProofAssume thaty∗=(y∗1,y∗2,...,y∗n)Tis the equilibrium point of system(4),theny∗satisfies

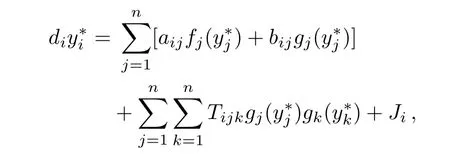
wherei=1,2,...,n.Firstly we show the existence of the equilibriumy∗of Eq.(4).Define a mapping as follows:F(y)=(F1(y),F2(y),...,Fn(y))T,where

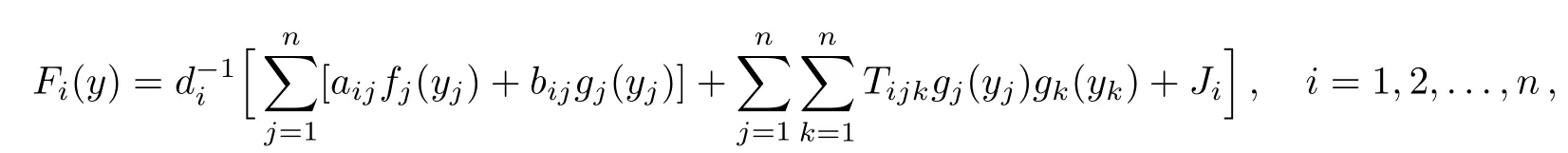
wherey∈[−χ,χ]nand

In view of(H),we have

Then we know thatF(y)maps a bounded set[−χ,χ]nto itself,wherey=(y1,y2,...,yn)T.According to the continuity of the nonlinear activation functionsfi(.)andgi(.),we can conclude thatF:[−χ,χ]n→[−χ,χ]nis continuous.In view of Brouwer fixed point theorem,there exists at least one fixed pointy∗∈[−χ,χ]nof the mappingF,i.e.,the equilibrium of Eq.(4).

Notice that the globally exponentially stability of the equilibriumy∗implies the uniqueness of the equilibrium,next we only prove the globally exponentially stability of the equilibriumy∗.

It follows from(H)and Eq.(4)that

whereD+denotes the upper right derivation.Consider the following function Θi(νi)defined by

whereνi∈[0,+∞),i=1,2,...,n.In view of Eq.(6),we have

where

By Eq.(10),we know that Θi(0)≥ρ(i=1,2,...,n).It is easy to see that Θi(νi)is continuous forνi∈[0,+∞)(i=1,2,...,n)and Θi(νi)→−∞asνi→+∞.Thus there exist constants¯νi∈(0,+∞)(i=1,2,...,n)such that

Choose 0＜ν∗＜min{¯ν1,¯ν2,...,¯νn},then we have

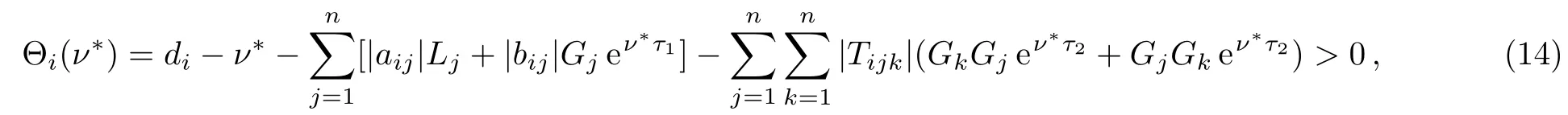
wherei=1,2,...,n.Define the following function:

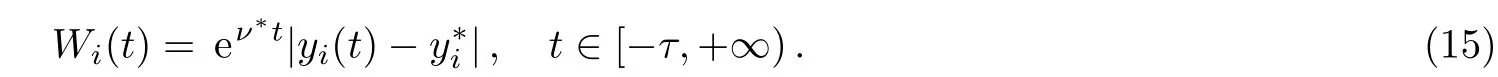
By Eqs.(9)and(15),we have

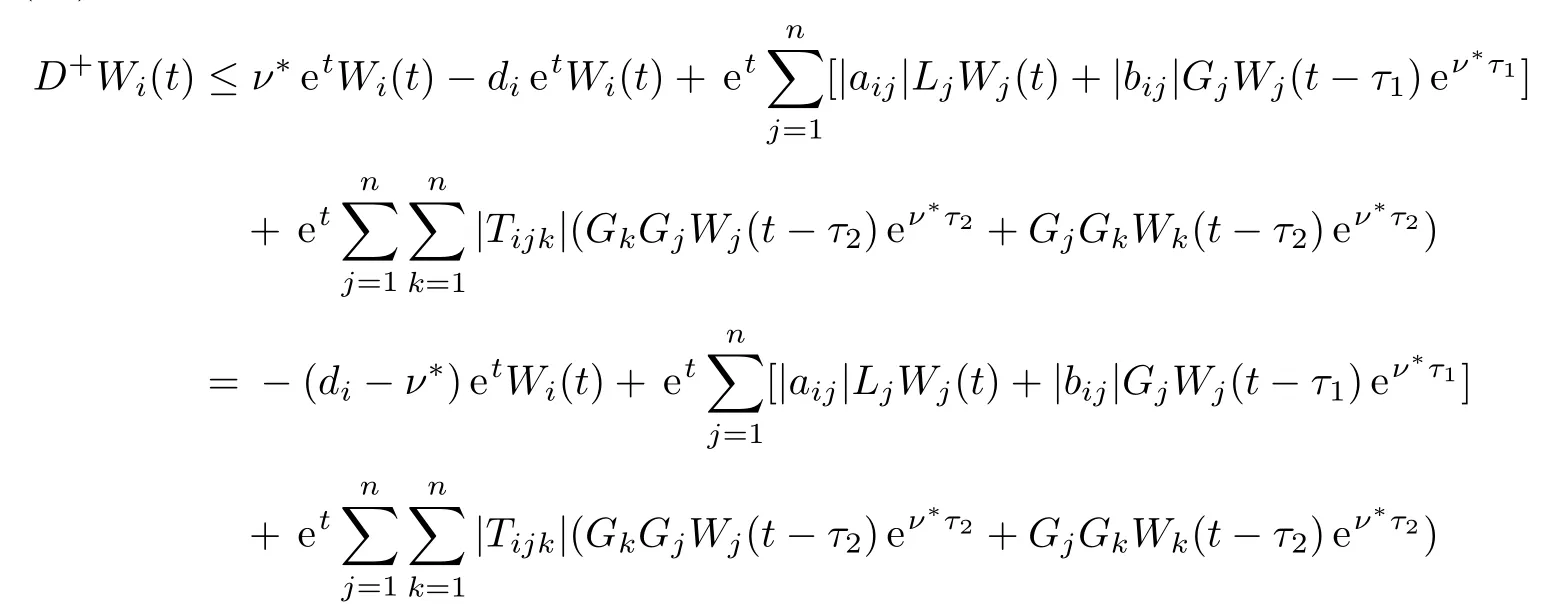
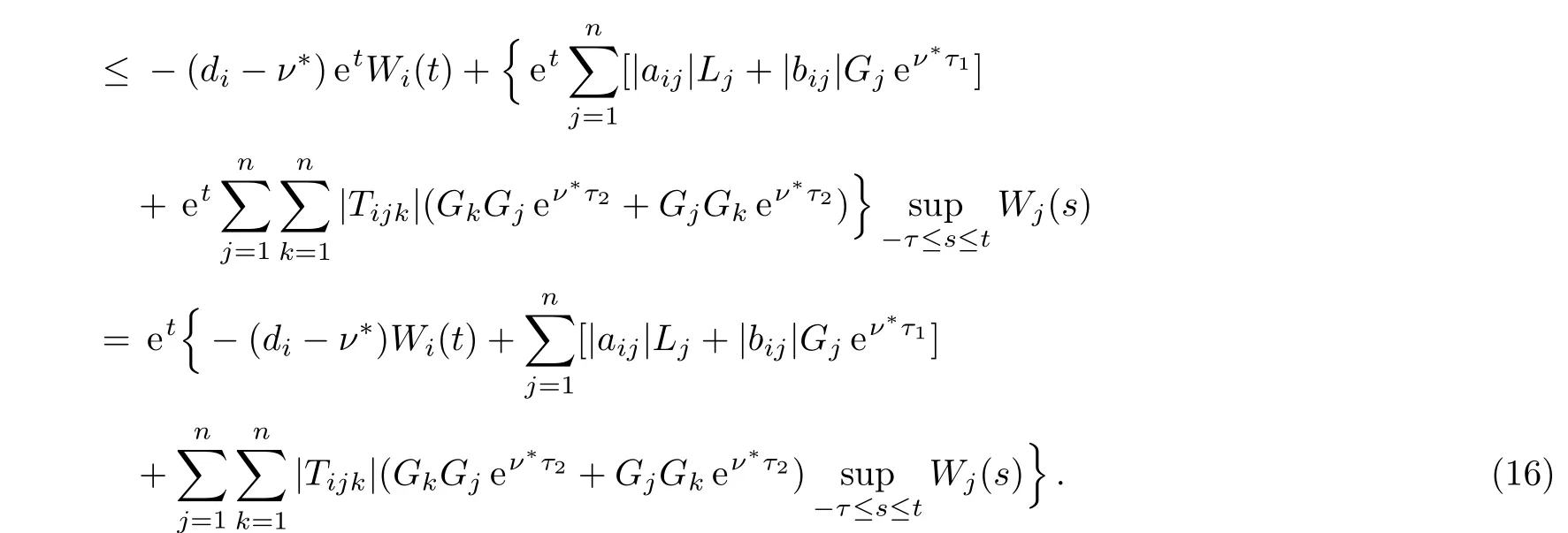
By Eq.(15),we know thatWi(t)≤ζ(i=1,2,...,n,t∈[−τ,0],whereζ＞0 is given by Eq.(5).We claim

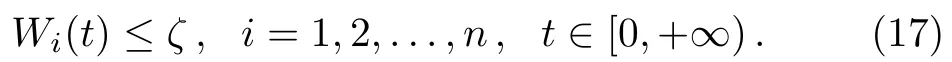
First we prove that

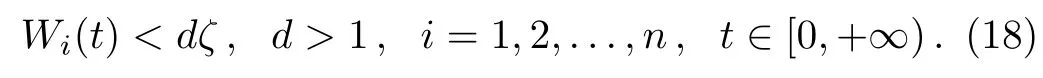
Assume that Eq.(18)does not hold,then there is one component amongWi(.)(say(Wk(.))and a first timet1＞0 such that

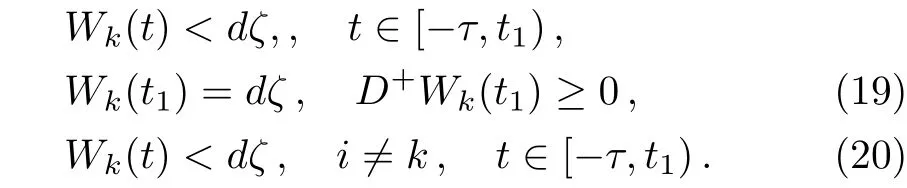
By Eqs.(16),(18),and(19),we have

In view of Eq.(14),we have 0≤D+Wk(t1)＜0,which implies a contradiction.Thus(18)holds fort＞0.Then whend→1 in(18),we get

Namely,Eq.(17)holds.It follows from Eqs.(15)and(17)that

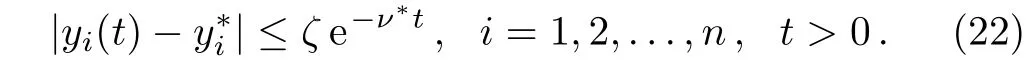
Let

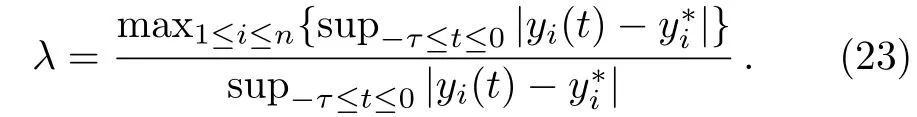
Thenλ≥1 and

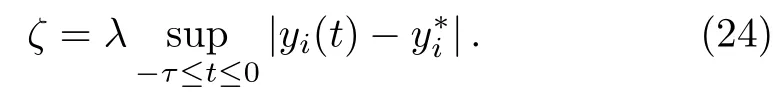
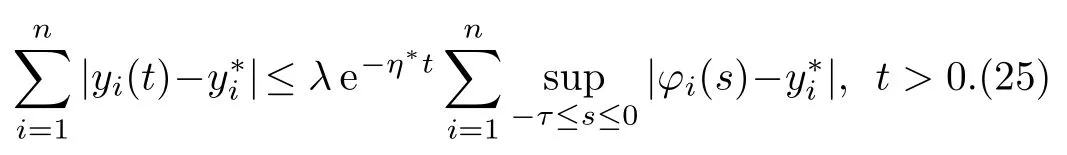
It follows from Eqs.(22)and(24)that Thus we can conclude thaty∗is globally exponentially stable.

Obviously,Eq.(25)implies that the equilibrium pointx∗of system(2)is globally exponentially stable.In fact,we can easily know that system(2)and(4)have the same equilibrium,i.e,x∗=y∗which meansx∗i=y∗i,i=1,2,...,n.By Eqs.(3)and(25),we get

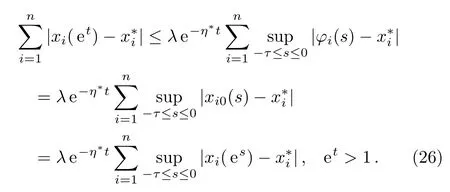
Let et=ς,thenς＞1 andt=logς＞0.Let es=ι,thens=logι∈[−τ,0]andι∈[q,1]in whichq=min{q1,q2}.Thus it follows from Eq.(26)that

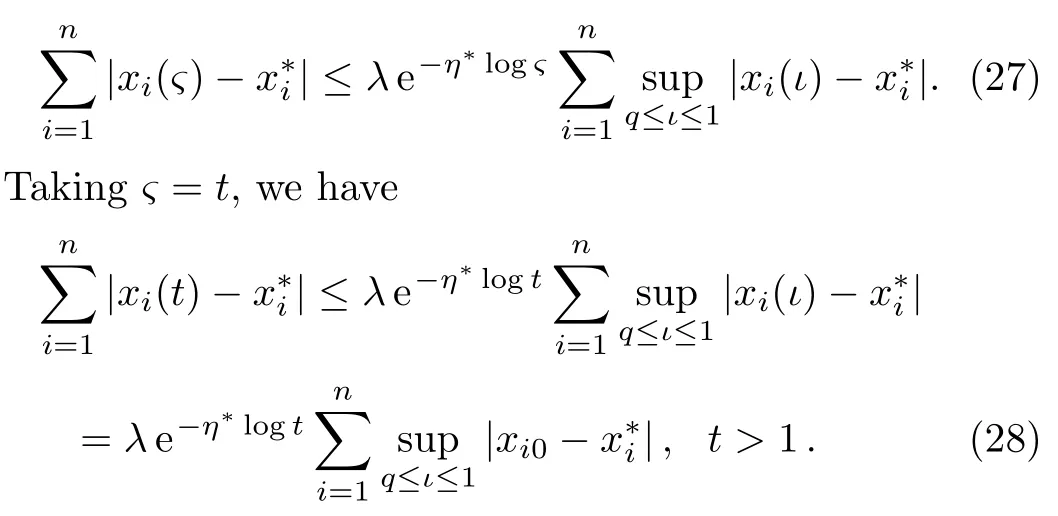
Thus we can conclude that the equilibrium pointx∗of system(2)is globally exponentially stable.The proof of Theorem 1 is complete.

In addition,in view of the proof of Theorem 1,we have the following result.

Theorem 2Under the condition(H),if there exists a positive constantν∗such that

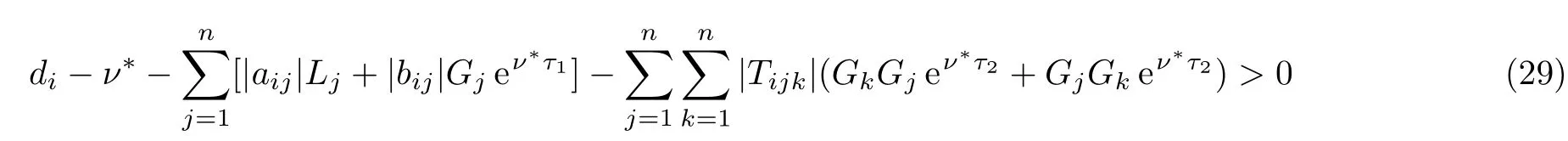
holds,then system(2)has a unique equilibriumx∗which is globally exponentially stable,wherei=1,2,...,n,τ1=−logq1≥0,τ2=−logq2≥0.

3 Examples

In this section,we give two examples to illustrate our main results derived in previous sections.Consider the following two high-order neural networks with proportional delays.

Example 1Consider the following high-order neural networks with proportional delays

where

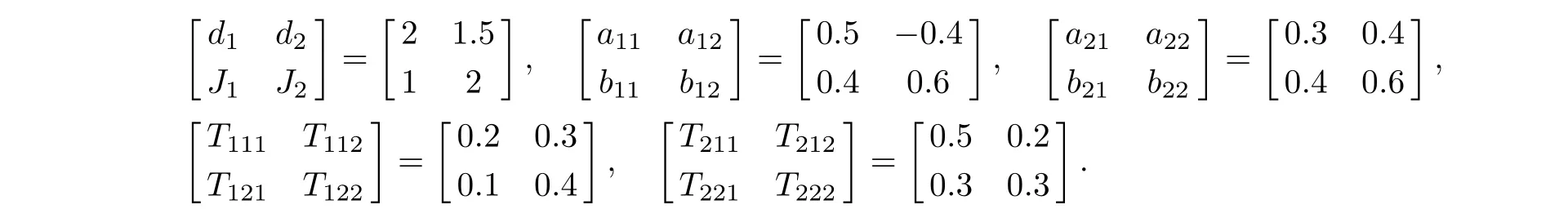
Letfi(xi)=gi(xi)=tanh(0.4xi),q1=0.5,q2=0.7,then we getLi=Gi=0.4,τ1=−log0.5=0.6931,τ2=−log0.7=0.3567,τ=0.6931,i=1,2.It is easy to check that

Then all the conditions(H)and(6)of Theorem 1 hold.Thus system(30)has a unique equilibrium(0.8576,2.7843)which is globally exponentially stable.The results are illustrated in Fig.1.

Example 2Consider the following high-order neural networks with proportional delays

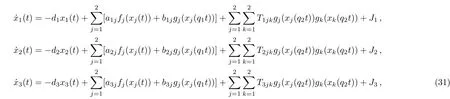
where

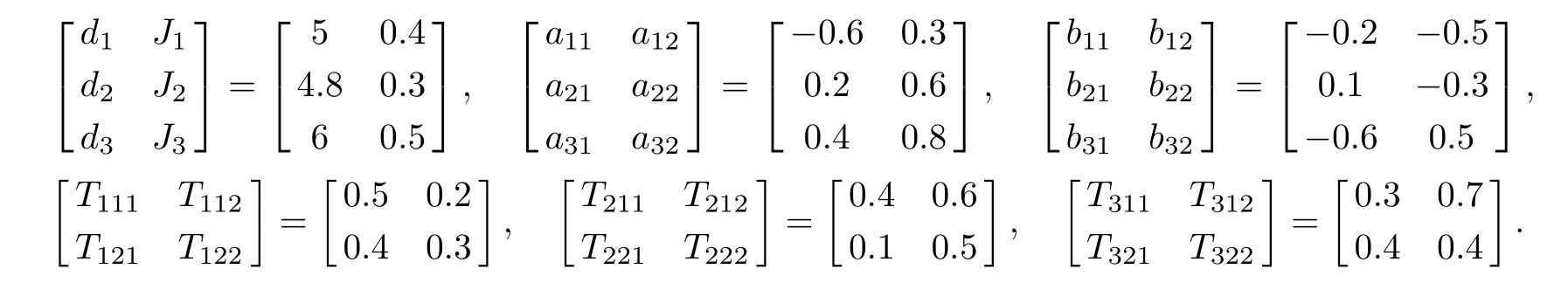
Letfi(xi)=gi(xi)=(1/2)(|xi+1|−|xi−1|),q1=0.4,q2=0.6,then we getLi=Gi=1,τ1=−log0.4=0.9163,τ2=−log0.6=0.5108,τ=0.9163,i=1,2.It is easy to check that

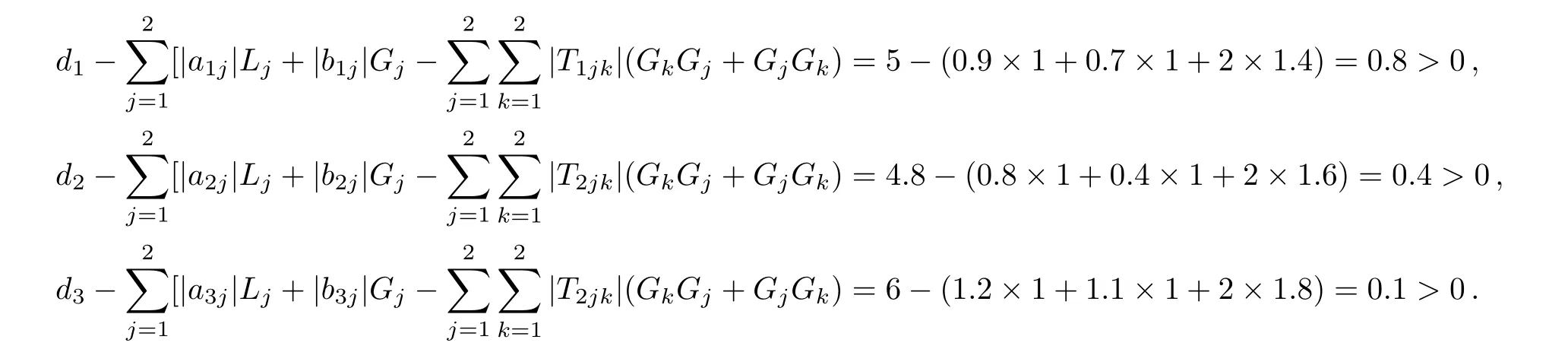
Then all the conditions(H)and Eq.(6)of Theorem 1 hold.Thus system(31)has a unique equilibrium(4.5022,2.4931,1.4872),which is globally exponentially stable.The results are illustrated in Fig.2.

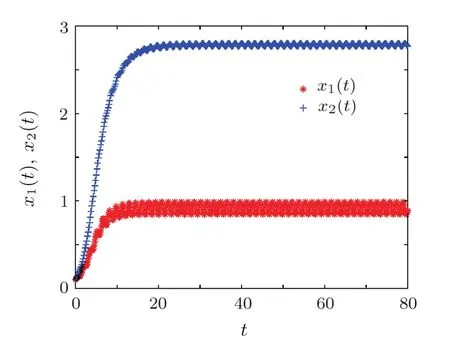
Fig.1 Transient response of state variables x1(t)and x2(t).

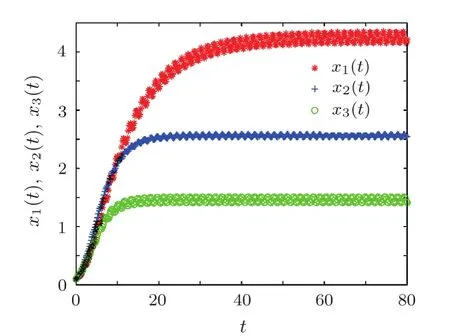
Fig.2 Transient response of state variables x1(t),x2(t),and x3(t).

4 Conclusions

In this paper,we have investigated the global exponential stability of high-order neural networks with proportional delays.By the nonlinear transformationyi(t)=xi(et)(i=1,2,...,n),we transform a class of high-order neural networks with proportional delays into a class of high-order neural networks with multi-constant delays and time-varying coefficients.Constructing the delay differential inequality which is similar to the Halanay inequality or generalized Halanay inequality,but is not the Halanay inequality or generalized Halanay inequality,we established the exponential stability conditions for the high-order neural networks with proportional delays.The obtained conditions are easily to check in practice.Finally,two examples are included to illustrative the feasibility and effectiveness.

[1]J.Nayak,B.Naik,and H.S.Behera,Ain Shams Eng.J.6(2015)1069.

[2]Y.K.Li and L.Yang,Appl.Math.Comput.242(2014)679.

[3]Q.Wang,Y.Y.Fang,H.Li,L.J.Su,and B.X.Dai,Neurocomputing 138(2014)339.

[4]F.Wang,Y.Q.Yang,and M.F.Hu,Neurocomputing 154(2015)239.

[5]J.Li,J.Yang,X.T.Yuan,and Z.H.Hu,Neurocomputing 131(2014)388.

[6]Q.T.Gan and R.Xu,Neural Process.Lett.32(2010)83.

[7]L.Duan,L.H.Huang,and Z.Y.Guo,Nonlinear Dyn.77(2014)1469.

[8]Y.K.Li,C.Wang,and X.Li,Neural Process.Lett.39(2014)247.

[9]J.Cao,R.Rakkiyappan,K.Maheswari,and A.Chandrasekar,Sci.China Technol.Sci.59(2016)387.

[10]F.L.Ren and J.D.Cao,Nonlinear Anal.:Real World Appl.7(2006)967.

[11]J.D.Cao,J.L.Liang,and J.Lam,Phys.D 199(2004)425.

[12]Y.Wan,J.D.Cao,G.H.Wen,and W.W.Yu,Neural Netw.73(2016)86.

[13]J.D.Cao and R.X.Li,Sci.China Infor.Sci.60(2017)032201.

[14]H.B.Bao,J.H.Park,and J.D.Cao,Neural Netw.81(2016)16.

[15]H.B.Bao and J.D.Cao,Nonlinear Anal.:Modelling Control 21(2016)306.

[16]L.Q.Zhou,X.B.Chen,and Y.X.Yang,Appl.Math.Comput.229(2014)457.

[17]D.J.Lu and C.J.Li,Neural Comput.Appl.23(2013)1.[18]C.J.Xu and Q.M.Zhang,Neural Process.Lett.40(2014)227.

[19]R.Rakkiyappan,C.Pradeep,A.Vinodkumar,and F.A.Rihan,Neural Comput.Appl.22(2013)55.

[20]H.C.Tsai,Neural Comput.Appl.27(2016)2465.

[21]M.Shafiq and N.R.Butt,Int.J.Control Auto.Syst.9(2011)489.

[22]Y.H.Xia,J.Appl.Math.Comput.32(2010)311.

[23]C.J.Xu,Y.F.Shao,and P.L.Li,Neural Process.Lett.42(2015)541.

[24]M.G.Hua,X.Z.Liu,F.Q.Deng,and J.T.Fei,Neural Process.Lett.32(2010)219.

[25]C.Wang,Neurocomputing 171(2016)1291.

[26]Y.H.Yu and W.D.Jiao,Neural Process.Lett.39(2014)167.

[27]Z.B.Chen and M.Q.Yang,Neural Comput.Appl.23(2013)2221.

[28]X.F.Liao,S.W.Li,and K.W.Wong,Nonlinear Dyna.31(2003)299.

[29]L.Q.Zhou,Neurocomputing 161(2015)99.

[30]L.Q.Zhou,Nonlinear Dyn.77(2014)41.

[31]L.Q.Zhou,Neural Process.Lett.38(2013)321.

[32]L.Q.Zhou,Nonlinear Dyn.73(2013)1895.

[33]C.Zheng,N.Li,and J.D.Cao,Neurocomputing 149(2015)1149.

[34]L.Q.Zhou,Neural Process.Lett.42(2015)619.