多楔带横向非线性振动的理论计算和实验研究

李占国，杨许刚

(1.长春工业大学 机电工程学院 长春130012；2.长春理工大学 机电工程学院，长春130022)

多楔带是由顶布、芯绳、楔胶、粘合胶经过硫化加工制成的复合材料体[1]，多楔带具有粘弹性，传动过程的横向振动多表现出非线性特性。1997年,J.MOON和J.A.WICKERT实验研究了由于带轮偏心激励引起的非线性振动，测量了前两阶模态振动的幅频曲线，发现振幅随频率有明显的跳跃现象[2]。2012年，刘金华实验研究了同步带和平带在匀速和变速横向振动中出现的周期、多倍周期和混沌运动[3]。本文计算了多楔带在不同激励频率下的非线性振动特性，最后试验验证了理论分析的正确性。

1 粘弹性特性实验

图1 多楔带的应力-应变曲线

多楔带的粘弹性是引起横向振动非线性的主要原因，为了确定多楔带的粘弹性特性，在拉伸试验机上，对4PK998多楔带进行0-5000N加载实验和5000-0N的卸载实验，加载速度为60mm/min。得到带的纵向应力-应变曲线如图1所示。多楔带在加载过程中，应力与应变近似成线性变化，而在卸载过程中，卸载曲线具有明显的弹性滞后现象。通过实验测量得到多楔带的弹性模量为1.9GPa，粘性阻尼系数为1.96×106N·s/m2。

2 非线性振动方程

将粘弹性多楔带的动力学模型简化为具有较小弯曲刚度的梁，设多楔带的密度为ρ，横截面积为A，轴向运动速度为v，张紧力为P,两带轮的中心距为L，EI为抗弯刚度，w表示横向振动位移，采用粘弹性Kelvin-Voit本构模型，利用牛顿第二定律，可得横向振动方程为[4]：

(1)

式中：E0为弹性模量，η为动态粘性阻尼系数。

在不同转速的运动过程中，横向振动幅度和弹性滑动程度不同，导致张紧力发生变化，即有：P=P0+P1cos(Ωt)，其中P0为张紧力波动幅值，Ω为张紧力波动频率。

引入无量纲参数：

(2)

得到粘弹性多楔带无量纲形式的横向非线性振动方程：

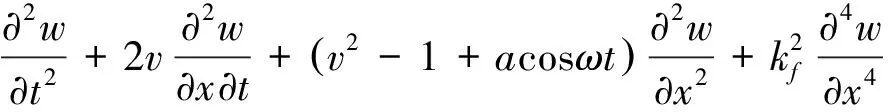
(3)

对应的无量纲形式的边界条件为：

(4)

对方程(3)进行一阶Galerkin截断可得常微分方程：

(5)

3 理论计算

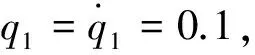
由式(2)可得理论计算对应的无量纲基本参数为k1=25.67,k2=111.7,kf=0.031,a=0.8，在主动轮的不同转速驱动下，多楔带横向振动所受的激励频率也不同，利用相图来研究激励频率对非线性振动的影响。主动轮转速为800rpm时，无量纲参数为v=0.068,ω=1，通过计算得到振动相图如图3所示，横向振动做3倍周期运动。主动轮转速为1200rpm时，无量纲参数为v=0.1,ω=1.5时的振动相图如图4所示，横向振动做2倍周期运动。

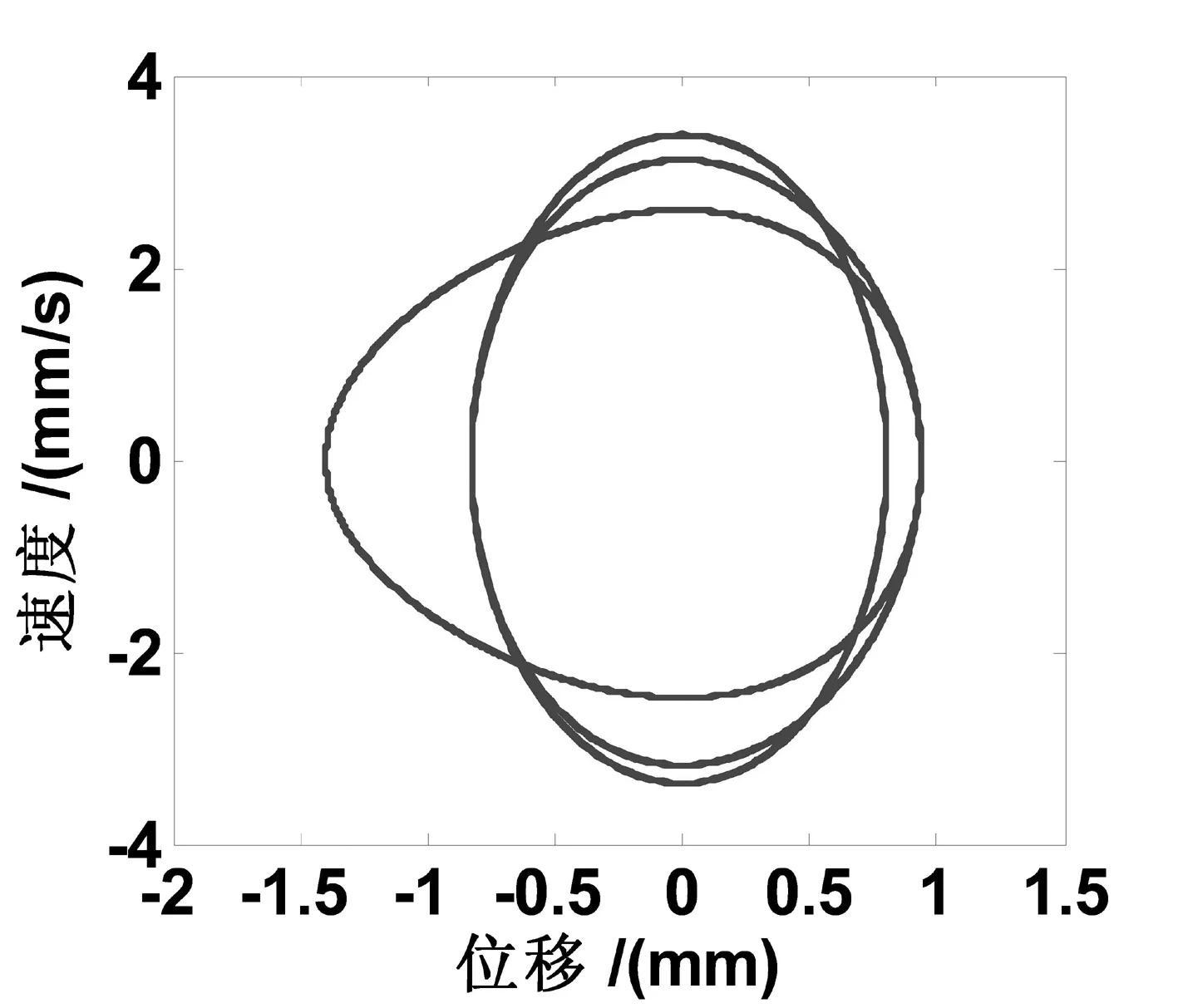
图3 800rpm时3倍周期运动相图

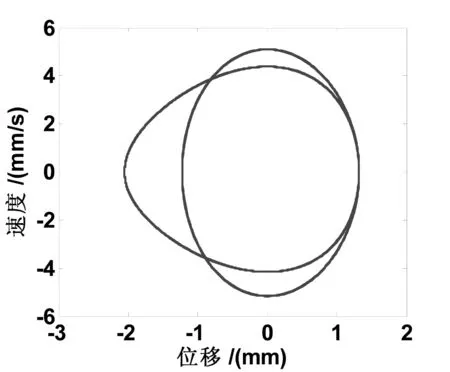
图4 1200rpm时2倍周期运动相图

4 实验研究

为了验证理论计算的正确性，进行多楔带的横向振动试验。振动试验是在型号为QCTDCC001的多楔带振动试验台上进行的，如图5所示。选用4PK998多楔带，带轮型号为P4PK96。选用欧姆龙ZX-LD40非接触式激光位移传感器，其采样频率为100Hz，测量系统原理如图6所示。施加张紧力为210N，试验测量了转速为800rpm和1200rpm时多楔带紧边中点的横向振动。

图5 多楔带横向振动测量设备

图6 试验测量系统示意图

当主动轮转速为800rpm时，测量得到的振动时域图和相图如图7所示。振动幅值为0.034mm,振动频率为3.62Hz，7.19Hz和10.81Hz，多楔带横向振动出现3倍周期运动。

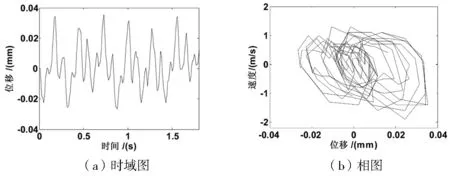
图7 800rpm横向振动的时域图和相图

当主动轮转速为1200rpm时，其振动的时域图和相图如图8所示，振动幅值为0.03mm，振动频率为5.6 Hz和11.1Hz，多楔带横向振动出现2倍周期运动。

图8 1200rpm横向振动的时域图和相图

理论计算和试验验证都表明，在800rpm下，横向振动出现3倍周期运动；在1200rpm下，横向振动出现2倍周期运动。由此可知：在不同的激励频率下，多楔带横向振动表现出非线性特性，出现多倍周期运动现象。

5 结语

本文理论计算了横向非线性振动出现的多倍周期运动，计算表明多楔带在800rpm和1200rpm不同激励频率下，紧边中点横向振动出现3倍周期和2倍周期运动，针对800rpm和1200rpm进行实验测量，实验表明：两种转速下多楔带的振动表现为3倍和2倍周期运动。这与理论分析吻合，说明了不同激励频率下，横向振动表现出多倍周期运动的非线性特性。

[1] 黄靖.多楔带及其生产工艺和设备[J].橡胶工业,2002,49(2):94-96.

[2] J Moon,J A wickert. Non-linear Vibration Of Power Transmission Belts[J].Journal of Sound and Vibration,1997,200(4):419-431.

[3] 刘伟,张劲夫.粘弹性传动带的分岔特性和混沌振动分析[J].动力学与控制学报,2005,3(3)：63-67.

[4] 张伟，温洪波，姚明辉.黏弹性传动带1:3内共振时的周期和混沌运动[J].力学学报，2004,36(4):443-454.