Mathematical Modelling and 3D FEM Analysis of the Influence of Initial Stresses on the ERR in a Band Crack’s Front in the Rectangular Orthotropic Thick Plate

Arzu Turan Dincel and Surkay D. Akbarov

1 Introduction

It is known that the linear theory of crack mechanics cannot take into consideration the uniformly distributed normal stresses acting along the crack’s edges under determination of Stress Intensity Factors (SIF) or Energy Release Rates (ERR) at the tips or fronts of the crack. Note that this state is caused with the linearity of the mathematical modelling as well as with the geometrical modelling of the crack. Nevertheless, up to now within the scope of the T-stress concept [Williams (1957); Rice (1974)] some attempts have been made to take into consideration the aforementioned normal stresses on the crack’s growth processwithin the scope of the linear theory of elasticity. We recall that the T-stress is the first nonsingular term in the expansion of the opening normal stress at the near vicinity of the crack’s tip or front and this stress has great significance for the prediction of the crack growth direction stability in the fracture of brittle materials [Cotterell and Rice (1980);Melin (2002); Pham, Bahr, Bahr, Fett, and Balke (2006)] and for the determination of the crack growth resistance in the fracture of ductile materials detailed in the paper [Tvergaard and Hutchinson (1994)] and others listed therein. These facts have pushed the researchers to develop mathematical methods for calculation and analysis of the T-stress, some of which are detailed in the papers [Sherry, France, and Goldthorbe (1995); Jogdand and Murthy (2010); Sutradhar and Paulino (2004); Chen (2000); Chen (2014)] and others reviewed therein. Nevertheless, the aforementioned T- stress concept cannot take into consideration the influence of the uniformly distributed normal stresses acting along the crack’s edge surfaces on the SIF or ERR. Note that， this influence can be modelled within the framework of the approach of which the equations and relations are obtained from linearization of the corresponding geometrically non-linear field equations and relations of the theory of elasticity. Under this linearization procedure, the stress-strain state regarding the uniformly distributed normal stresses acting along the crack’s edge surfaces is taken as the initial stresses, and the non-linear equations and relations are linearized around this initial state and in this way the linearized theory of elasticity is constructed. Consequently,the corresponding crack problems are studied within the scope of this linearized theory, of which the coefficients of the equations and relations contain the aforementioned initial stresses [Guz (1999)]. The fundamentals of the application of the linearized theory on the corresponding crack problems are proposed and detailed in the monograph [Guz (1983)]which also contains many concrete results. A review of more recent results related to the linearized (or so-called, non-classical) crack problems can be found in the papers [Guz(2000); Guz, Dyshel, and Nazarenko (2004)]. However, the results detailed in the works[Guz (1983); Guz (2000); Guz, Dyshel, and Nazarenko (2004)] relate to the micro-crack problems, i.e. to the problems related to the cracks contained in the infinite or semi-infinite elastic medium. Note that up to now some investigations have also been made related to the macro-crack problems [Akbarov and Turan (2009); Akbarov and Turan (2011);Akbarov and Yahnioglu (2016)], the results of which are also detailed in the monograph[Akbarov (2013)]. Moreover, a mixed boundary value problem for an embedded crack in an orthotropic strip is considered in the paper [Yusufoglu and Turhan (2012)]. At the same time, it should be noted that these investigations are carried out for the two-dimensional(plane-strain state) problems and up to now there have not been any investigations regarding the corresponding 3D crack problems. Therefore, in the present paper we attempt to consider and investigate the 3D problem for the band crack contained in the rectangular plate made of anisotropic (orthotropic) material. It is assumed that at first (i.e. in the initial state) the plate's two opposite lateral edge planes are loaded by uniformly distributed normal stretching or compressing forces and then the crack’s edge surfaces are loaded with the additional uniformly distributed normal opening forces. It is required to investigate how the uniformly normal initial stresses acting along the crack's edge planes influence the ERR at the band crack front caused with the aforementioned additional opening normal forces acting on the crack's edge planes. Moreover, the influence of the anisotropy properties of the plate material and the crack location with respect to the plate thickness on the ERR is studied.

2 Formulation of the problem

Consider a rectangular plate and associate the Cartesian coordinate systemwith this plate (Fig. 1). The position of the points of the plate we determine through the Lagrange coordinates in this system. Assume that the plate contains a band crack, the edge planesurfaces of which are parallel to the plate’s face planes. Moreover, we assume that the plate occupies the region

In (1) and (2) the following notation is used:() is the plate length in the(axis direction,is the band crack length in theaxis direction,is the plate thickness, andis the distance of the crack located plane from the lower face plane of the plate (Fig.1).

Figure 1: The sketch of the rectangular plate containing the band crack.

According to the well-known procedure, in the case under consideration the initial stresses caused by the forces with intensitycan be determined as follows

Now we consider formulation of the problem related to the stress-strain state caused by the additional opening normal forces acting on the crack’s edge planes. For this purpose we use the so-called three dimensional linearized equations and relations which, for the case under consideration, can be written as follows.

Equilibrium equations and strain-displacement relations.

In (4) and repeated below, () are summed over their ranges and conventional notation is used.

According to [Lekhnitskii (1963)], the constitutive relations for the plate material can be written as follows.

Now we consider formulation of the boundary conditions which for the case under consideration are selected as follows.

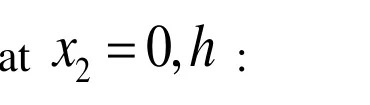
Boundary conditions on the crack’s edge surfaces:

Thus, this completes the formulation of the problem, according to which, the determination of the stress-strain state in the rectangular plate containing the band crack is reduced to the solution to the equations (3) – (6) within the scope of the boundary condition given in (7).

3 Method of solution and 3D FEM modelling for calculation of the ERR

As the analytical solution to the problem formulated above is impossible, we attempt to solve it by utilizing the 3D Finite Element Method (FEM). For this purpose, according to[Guz (1999)], we introduce the following functional.

After some mathematical manipulations, we can represent the equation (9) as follows.

equilibrium equation in (4) and the boundary conditions with respect to the forces in (7)are obtained and in this way, the validity of the functional (8) for the 3D FEM modelling of the boundary value problem under consideration is proven. Note that similar type functional was also used in the paper [Babuscu Yesil (2017)] for investigation of the forced vibration of the pre-stressed rectangular plate with cylindrical cavities.

Note that under the FEM modelling of the crack's front we also use ordinary finite elements,i.e. under this modelling the so-called singular finite elements are not introduced. This is because the investigations carried out in [Akbarov and Turan (2011); Akbarov and Yahnioglu (2016), Akbarov (2013)] show that the use of the singular finite elements under finite element modelling of the crack's tip changes the values of the ERR in an insignificant amount. Moreover, we note that under FEM modeling thecan be also selected as rectangular prisms with nodes the number of which greater than eight. For instance, thecan be presented as a 32-node hexahedral element described in [Fan, Zhang, Dong, Li and Atluri (2015)].

Thus, employing the well-known Ritz technique [Zienkiewicz and Taylor (1989)] for the case under consideration we solve numerically the boundary value problem formulated above and in this way we determine the stress-strain state in the plate. After this determination, we calculate the ERR at the crack front with the use of the following algorithm.

First, according to the expression

Note that under calculation of, the magnitude of the areais determined from the convergence of the numerical results obtained forwith decreasing of.

4 Numerical results and discussions

Below, in consideration of the numerical results, the influence of the initial stress on the ERR will be estimated through the ratio, however, the influence of the mechanical constants, i.e. the orthotropic properties of the plate material will be estimated through theMoreover, under this consideration we introduce the ratiosNote that under obtaining these results it is assumed that

All the numerical results which will be discussed below are obtained in the case where the

Table 1: The values of SIF atobtained for various values of the ratio in the case where the material of the plate is isotropic and the initial stress in the plate is absent.

Table 1: The values of SIF atobtained for various values of the ratio in the case where the material of the plate is isotropic and the initial stress in the plate is absent.

?

Table 2: The influence of the ratioon the values ofin the various, and in the case where ,,0.25 and .

Table 2: The influence of the ratioon the values ofin the various, and in the case where ,,0.25 and .

?

-0.01 30.9739 31.4613 31.9778 31.2755 29.091 24.397 16.496 0.1 0 17.3966 17.5582 18.0691 18.0336 17.364 15.341 11.140 0.01 11.3317 11.3797 11.7095 11.8273 11.688 10.779 8.3722-0.01 34.7238 34.9761 35.0308 34.5291 33.101 29.277 22.752 0.05 0 19.7975 19.8684 19.8775 19.8259 19.414 18.758 15.873 0.01 13.0817 13.1043 12.9833 12.9796 13.100 13.208 12.239

Table 3: The influence of the ratioon the values ofin the various, and in the case where ,,0.25 and .

Table 3: The influence of the ratioon the values ofin the various, and in the case where ,,0.25 and .

?

Table 4: The influence of the ratioon the valuesin the case where ,,0.25 and .

Table 4: The influence of the ratioon the valuesin the case where ,,0.25 and .

At the same time, the results given in Tabs. 2, 3 and 4 show that a decrease in the values of the shear modulus magnitude of this increase is considerable. However, the influence of a decrease of the shear moduluson the ERR is insignificant. Besides all of these, the foregoing results show that the initial stretching (compressing) of the plate in theaxis direction (Fig. 1)causes a decrease (an increase) in the values of the ERR. Note that the influence of the initial stress on the values of the ERR depends also on the geometrical parameters such as

?

Table 5: The values of calculated atand obtained for variousand in the case where ,,and .

Table 5: The values of calculated atand obtained for variousand in the case where ,,and .

?

Table 6: The values of calculated atand obtained for various and in the case where ,,and .

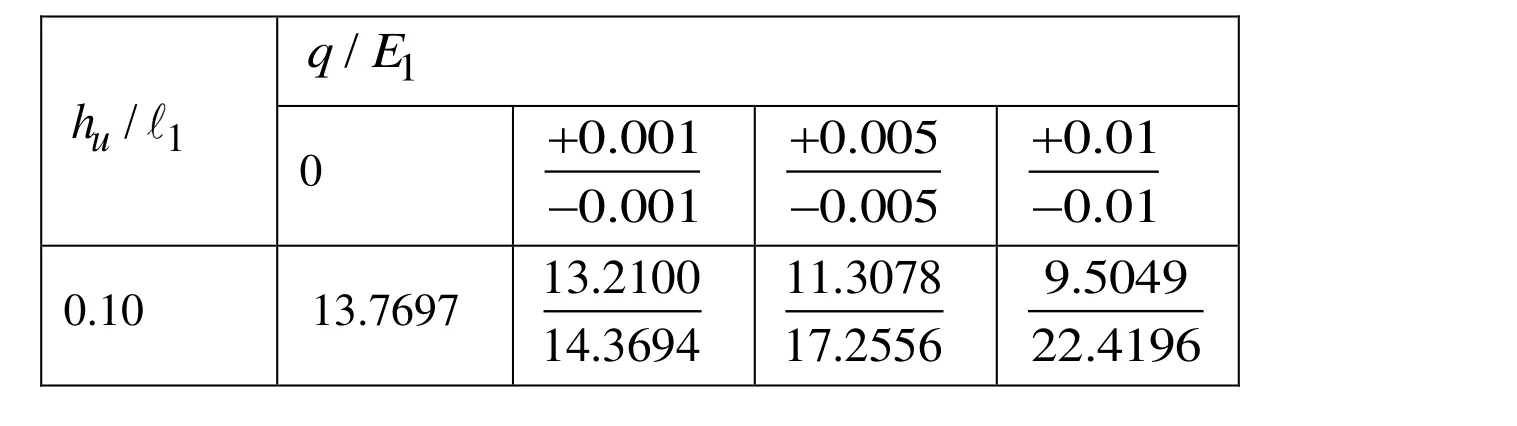
Table 6: The values of calculated atand obtained for various and in the case where ,,and .

?

?

Table 7: The influence of the ratiosin the case where

?

Figure 2: Graphs of the dependence betweenandconstructed for various in the cases where (a) and (b) under,,and .

Figure 3: Graphs of the dependence between various in the cases where (a) and (b) under,,and .

We recall that all the numerical results discussed above are obtained in the cases whereand it is established that the initial stretching of the plate causes a decrease, but the initial compression causes an increase of the ERR. The detailed numerical investigation carried out for the cases whereshows that the character of the influence of the initial stress of the plate on the ERR remains valid before a certain value of the ratiobut after this the character changes. In other words, in the casesthe initial stretching of the plate causes an increase, but the initial compression causes a decrease of the ERR. For a clear illustration of this statement,we consider the graphs of the dependence betweenThese graphs are given in Figs. 4 and 5 which are constructed for variousunder,the cases whereand for the cases where

Figure 4: The graphs of the dependence between

Figure 5: The graphs of the dependence between the ERR change

5 Conclusions

Thus, in the present paper, the mathematical modelling and 3D FEM study of the ERR are undertaken in the band crack’s front contained in the orthotropic thick rectangular plate which is stretched or compressed initially before the loading of the crack's edge planes.The initial stretching or compressing of the plate causes the uniformly normal stress acting in the direction which is parallel to the plane on which the band crack is located, to appear.After the appearance of the initial stress in the plate it is assumed that the crack's edge planes are loaded with additional uniformly distributed normal forces and the ERR caused with this additional loading is studied.

The corresponding boundary value problem is formulated within the scope of the so-called 3D linearized theory of elasticity which allows us to take into consideration the initial stress on the values of the ERR but it is impossible to study this influence within the scope of the 3D linear theory of elasticity. Under formulation of the problem related to determination of the stress-strain state which is caused by, among other conditions, the aforementioned additional loading acting on the crack’s edge planes on the plate ends， it is also assumed that the displacement along the plate thickness is equal to zero.

The problem under consideration is solved numerically by employing the 3D FEM.Numerical results on the influence of the initial stress, orthotropic properties of the plate material， crack’s length and its distance from the upper face plane of the plate on the values of the ERR, are presented and discussed. According to these results and discussions the following concrete conclusions can be drawn.

· Before a certain length of the crack’s band， the initial stretching of the plate causes a decrease, but that initial compression causes an increase in the values of the ERR;

· In the cases where the crack’s band length is less than the aforementioned “certain length”， the character of the influence of the initial stress on the ERR changes and this change may be caused by the restriction of the band’s ends opening displacement;

· The magnitude of the influence of the initial stress on the ERR increases with the crack length and with the convergence of the crack to the plate’s upper plane;

· A decrease in the values of the shear modulus of the plate material in the planes which are perpendicular to the crack’s location plane causes a considerable increase in the values of the ERR;

· Under initial compression of the plate, the values of the ERR approach infinity with the approaching of the absolute values of the initial compression force to the critical force which causes the buckling-delamination of the plate around the band crack;

· Under a relatively greater length of the crack's band, the values of the ERR obtained in a certain part of the crack's front which is around the center of this front along the band direction, can be taken as the corresponding ones related to the plane strain state.

Akbarov, S. D.; Turan, A.(2009): Mathematical modelling and the study of the influenc e of initial stresses on the SIF and ERR at the crack tips in a plate-strip of orthotropic mat erial.Appl. Math. Model,vol. 33, no. 9, pp. 3682 - 3692.

Akbarov, S. D.;Yahnioglu, N.(2010): Delamination buckling of a rectangular orthotropic c omposite plate containing a band crack.Mech. Comp. Mater, vol. 46, no. 5, pp. 493 - 504.

Akbarov, S. D.;Yahnioglu, N.;Karatas, E.E.(2010): Buckling delamination of a recta ngular plate containing a rectangular crack and made from elastic and viscoelastic compo site materials.Int. J. Solid Structures, vol. 47, no 25, pp. 3426 - 3434.

Akbarov, S. D.; Turan, A.(2011): On the energy release rate at the crack tips in a finite pre-strained strip.CMC Comp. Mater. Cont., vol.24, no. 3, pp. 257 - 270.

Akbarov, S. D.(2013):Stability Loss and Buckling Delamination: Three-dimensional Li nearized Approach for Elastic and Viscoelastic Composites. Springer, Verlag - Berlin.

Akbarov, S. D.;Yahnioglu, N.(2016): On the total electro-mechanical potential energy and energy release rate at the interface crack tips in an initially stressed sandwich plate-str ip with piezoelectric face and elastic core layers.Int. J. Solids Structures, vol. 88-89, pp.1 19-130.

Babuscu, Y.U.(2017): Forced and natural vibrations of an orthotropic pre-stressed rectan gular plate with neighboring two cylindrical cavities.CMC Comp. Mater. Cont., vol. 53,no. 1, pp. 1-23.

Chen, Y.Z.(2000): Closed form solutions of T-stress in plane elasticity crack problems.Int. J. Solids. Struct, vol. 37, no. 1, pp. 1763- 1783.

Chen Y. Z.(2014): Evaluation of the T-stress for multiple cracks in an elastic half-plane using singular integral equation and Green’s function method.Appl. Math. Comp, vol. 22 8, pp. 17-30.

Cotterell, B.; Rice, J. R.(1980): Slightly curved or kinked cracks.Int. J. Fract, vol. 16, n o. 2, pp. 155-169.

Fan, Q.; Zhang, Y.; Dong, L.; Li, S.; Atluri, S. N.(2015): Static and dynamic analysis of la minated thick and thin plates and shells by a very simple displacement-based 3-D hexahedral element with over-integration.CMC Comp. Mater. Cont., vol.47, no. 2, pp. 65 - 68.

Guz, A. N.(1983):Brittle Fracture Mechanics of Prestressed Materials, Naukova Dumk a, Kiev (in Russian).

Guz, A. N.(1999):Fundamentals of the Three-dimensional Theory of Stability of Deform able Bodies, Springer, Verlag-Berlin.

Guz, A. N.(2000): Description and study of some nonclassical problems of fracture mech anics and related mechanisms,Int. Appl. Mech., vol. 36, no.12, pp. 1537-1564.

Guz, A. N.; Dyshel, M. S.; Nazarenko, V. M.(2004): Fracture and stability of materials and structural members with cracks: approaches and results.Int. Appl. Mech., vol. 40, no.12, pp. 1323-1359.

Jogdand, P. V.; Murthy, K. S. R. K.(2010): A finite element based interior collocation method for the computation of stress intensity factors and T-stresses.Eng. Fract. Mech., v ol. 77, no. 7, pp. 1116-1127.

Lekhnitskii, S. G.(1963):Theory of Elasticity of an Anisotropic Body, Holden Day, San Francisco.

Melin, S.(2002): The influence of the T-stress on the directional stability of cracks.Int. J.Fract., vol. 114, no. 3, pp. 259-265.

Pham, V. B.; Bahr, H. A.; Bahr, U.; Fett, T.; Balke, H.(2006): Crack paths and the proble m of global directional stability.Int. Journal of Fracture, vol. 141, no. 3-4, pp. 513-534.

Rice, J. R.(1974): Limitations to the small, scale yielding approximation of elastic–plasti c crack-tip fields.J. Mech. Phys. Solids, vol. 22, pp.17-26.

Shah, O. R.; Tarfaoui, M.(2017): Determination of mode I & II strain energy release rat es in composite foam core sandwiches. An experimental study of the composite foam cor e interfacial fracture resistance.Composites Part B, vol. 111, pp. 134 - 142

Sih, G.(1973):Handbook of Stress Intensity Factors, Lehigh University.

Sherry, A. H.; France, C. C.; Goldthorpe, M. R.(1995): Compendium of T-stress solut ions for two and three dimensional cracked geometries.FatigueFract.Eng. Mater. Struc t., vol. 18, pp. 141–155.

Sutradhar, A.; Paulino, G. H.(2004): Symmetric Galerkin boundary element computati on of T-stress and stress intensity factors for mixed-mode cracks by the interaction integr al method.Eng. Anal. Boundary Elem., vol. 28, no. 11. pp. 1335-1350.

Tvergaard, V.; Hutchinson, J. V.(1994): Effect of T-stress on mode I crack growth resi stance in a ductile solid. Int. J. Solids. Structures, vol. 31, no. 6, pp. 823-833.

Williams, M. L. (1957): On the stress distribution at the base of a stationary crack.ASME J. Appl. Mech., vol. 22, pp. 111-114.

Yusufoglu, E.; Turhan, I.(2012): A mixed boundary value problem in orthotropic strip containing a crack,J. Franklin Inst, vol. 349, no. 6, pp. 2750-2769.

Zienkiewicz, O. C.; Taylor, R. L.(1989):The Finite Element Method, Basic Formulatio n and Linear Problems, 4-th ed., vol.1, McGraw-Hill Book Company, London, 1989.