基于Weibull分布的变压器恒加试验可靠性统计分析*
2018-01-22冯雪峰尹继东
冯雪峰, 尹继东
(西南交通大学 数学学院,成都 611756)
加速寿命试验(Accelerated life test,ALT)是在进行合理的工程及统计假设的基础上,利用与物理失效规律相关的统计模型,通过提高试验应力来使产品加速失效,再利用加速模型来外推产品在正常应力水平下的各种可靠性指标的一种寿命试验方法.采用ALT技术可实现对高可靠度长寿命产品可靠性水平的快速评定,它受到了国内外可靠性工作人员的高度重视,并在机械电子,武器装备及航空航天等领域得到了广泛应用[1-3].ALT包括恒定应力ALT(简称恒加试验),步进应力ALT(简称步加试验)和序进应力ALT(简称序加试验).
目前,ALT的研究主要集中在加速模型,ALT数据的统计分析以及ALT的优化设计方面.在加速模型方面,典型的加速模型有逆幂律(Inverse power)模型,Coffin-Manson模型等.逆幂律模型描述了诸如电压或压力这样的应力与产品寿命之间的关系[4].在ALT数据的统计分析方面,王炳兴等(2002)[5]基于恒加速试验数据研究了Weibull分布下可靠度的渐近无偏估计及渐近置信区间;Watkins(2008)[6]基于Weibull分布的恒加试验数据提出了一种简化的极大似然估计方法,研究表明简化的极大似然估计方法提高了计算效率和模型参数估计值的稳健性;郑光玉等(2013)[7]在两参数广义指数分布下研究了自适应逐步Ⅱ型混合截尾恒加试验的统计分析方法.在ALT的优化设计方面,钱萍(2009)[8]提出了航天电连接器综合应力加速寿命试验优化方案,优化方案大大减少了试验次数,提高了试验数据的估计精度;陈文华等(2010)[9]以正常应力下产品中位寿命估计值的方差最小化为准则,利用极大似然估计理论和累积失效模型,提出了步加试验的优化方案;李新翼等(2013)[10]建立了广义指数分布定时截尾简单步加试验的数学模型,以正常应力水平下一段时间内可靠度估计值的渐进方差最小为准则,研究了试验的最优设计方案等.
在ALT中,恒加试验的优点是统计精度高,理论和方法成熟.常用的Weibull分布的参数估计方法有极大似然估计(MLE),最小二乘估计和矩估计法,MLE和LSM相比较而言,虽然用MLE法得到的模型参数的均方误差最小,但通常需要采用数值计算来求解模型参数的估计值;而LSM的原理简单且计算复杂度小,在大多数场合都能得到广泛的应用.因此,以某型变压器恒加试验数据为研究对象,采用LSM估计逆幂律-Weibull统计模型的未知参数,并利用加速模型对正常应力水平下的各种可靠性指标进行统计推断.
1 逆幂律-Weibull统计模型
变压器在工作期间,电压是影响其可靠性的最主要因素[4].在电应力作用下,变压器的寿命T服从双参数Weibull分布,其累积分布函数为
(1)
式(1)中:m>0为形状参数,η>0为特征寿命或尺度参数.
逆幂律-Weibull统计模型假设如下:
A1在电应力水平Si下,产品的寿命服从双参数Weibull分布W(mi,ηi),mi>0和ηi>0 (i=0,1,…,k)分别为应力水平Si下的形状参数和特征寿命.
A2在各电压应力水平Si下,Weibull分布的形状参数m是保持不变,即产品的失效机理保持不变.
A3产品的特征寿命ηi与电应力水平Si间满足对数线性加速模型:
lnηi=β0+β1·φ(Si),i=0,1,…,k
(2)
式(2)中:φ(Si)=lnVi,β0,β1为待估参数;Si是电压应力水平.
上述假设是否成立,获取试验观测数据后都可以进行检验.检验方法分别可采用: 范·蒙特福特检验法,巴特利特检验法和相关系数检验法[11].
2 逆幂律-Weibull统计模型的假设检验
2.1 威布尔分布的假设检验
在对各电压应力Si下的寿命数据进行统计分析之前,首先要检验样本数据是否服从Weibull分布.假设产品的寿命分布为F(t),则要检验假设:
H0:F(t)=F0(t;m,η)=1-exp{-(t/η)m}
基于截尾(定时或定数)样本数据t1≤t2≤…≤tr,采用范·蒙特福特检验法[11]来检验假设H0是否成立.令
则xi和Zi分别是来自极值分布和标准极值分布的第i个次序统计量,i=1,2,…,r,其中μ=lnη,σ=1/m为未知参数.范·蒙特福特提出统计量:
并证明了在H0成立下,诸Gi渐近独立且服从标准指数分布.把Gi均分为两组,则统计量:
在H0成立下的条件下,渐近服从第一自由度为2(r-r′-1)和第二自由度为2r′的F分布,其中r′=[r/2].对于给定的显著性水平α,如果
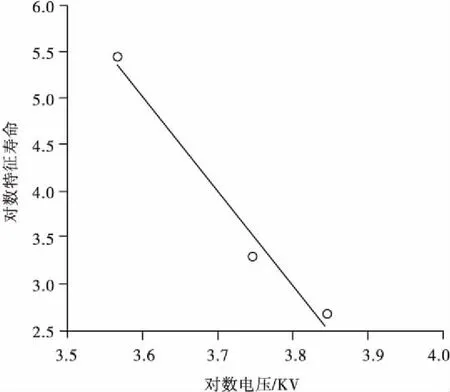
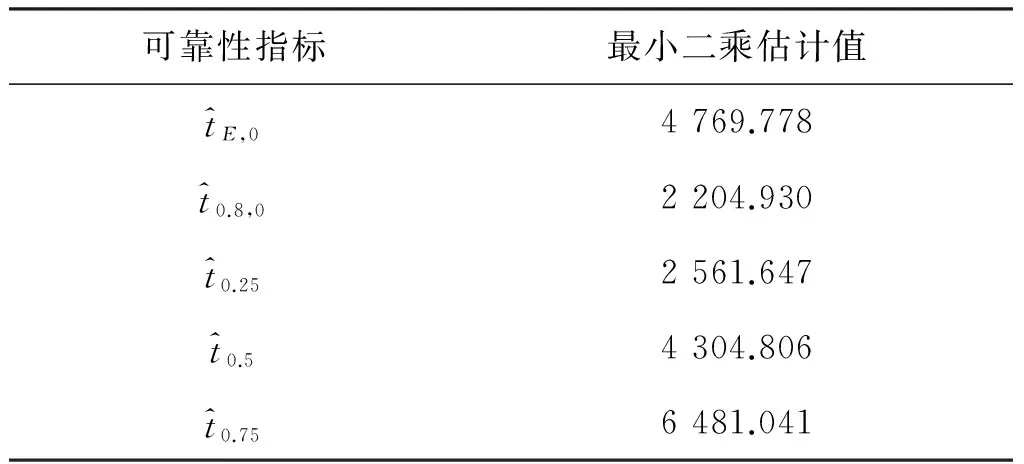
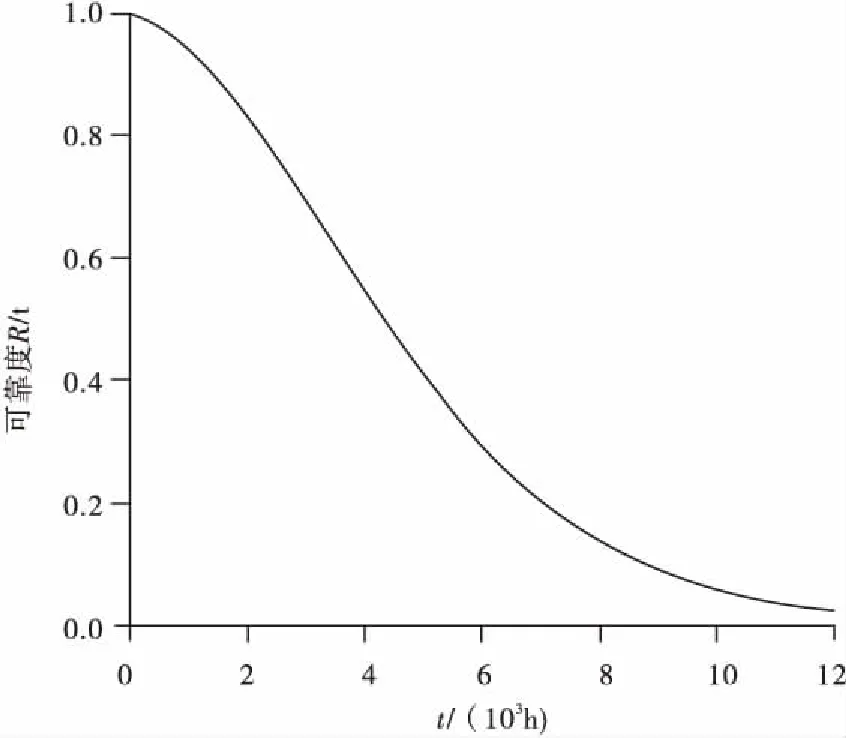
F F>F1-α/2(2(r-r′-1),2r′). 则认为H0不成立,否则可认为该截尾样本来自Weibull分布,其中Fα(f1,f2)是第一自由度为f1,第二自由度为f2的F分布的α分位数. 威布尔分布W(mi,ηi)中的形状参数mi不变的检验可采用巴特利特检验法[11],首先提出假设: H0:m1=m2=…=mk 根据巴特利特检验统计量的构造,记 试验应力水平Si与特征寿命ηi间是否满足对数线性关系,即对数电压lnφi与对数特征寿命lnηi间是否存在线性关系: 这需要进行检验.通常采用相关系数检验法来度量变量间是否存在线性关系及线性关系程度的强弱.首先计算样本相关系数: (3) 在显著性水平α下,若|r|>rα成立,则认为样本中φi与yi相关,这意味着选取的对数线性加速模型可用;若|r|≤rα成立,则认为样本中φi与yi不相关,这意味着选取的对数线性方程不能刻画特征寿命与试验应力间的关系. 对于Weibull分布,恒加试验数据统计分析方法有: 最小二乘估计(LSM),基于次序统计量各类线性估计,极大似然估计(MLE)和图估计等.LSM具有方法简单和计算容易的优点,因此得到广泛应用. 若产品的寿命T服从双参数Weibull分布,对式(1)两边进行两次对数变换可得: ln[-ln(1-FT(t))]=mlnt-mlnη (4) 若记 (5) 则方程(4)可化为线性方程: y=mx+b (6) 式(6)中:b=-μ/σ,μ=lnη,σ=1/m. 利用应力水平Si下的寿命试验数据ti1ti2…tiri,累积失效概率Fi(tij)可用中位秩公式(7)进行计算: (7) 从而获得试验数据: (tij,Fi(tij)),j=1,2,…,ri (8) 根据式(5),恒加试验数据就可以转化到新的坐标系(x,y)下,即式(8)转化为 (lntij,ln[-ln(1-Fi(tij))])=(xij,yij) (9) 采用LSM拟合式(9)的试验数据[12],拟合直线的系数bi和mi的最小二乘估计值为 (10) (11) (12) 设x=φ(S),y=lnη,则线性回归模型为 y=β0+β1x+ε (13) (14) 相应的回归方程为 (15) 为获得某型变压器在正常电应力水平15.8 KV下的p分位数寿命tp和可靠度为R的可靠寿命tR,0的估计,对型变压器进行3个应力水平的恒加试验,获得试验数据如表1所示.现基于表1列举的恒加试验数据来对型变压器进行可靠性统计分析.采用的统计分析软件为R软件[13]. 表1 恒定应力加速寿命试验数据Table 1 Data of constant-stress accelerated life test 采用范·蒙特福特检验法对表1的恒加试验数据进行Weibull分布的假设检验,其检验结果如表2所示. 表2 Weibull分布拟合优度检验结果Table 2 Goodness of fit test results for Weibull distribution 在显著性水平α=0.1下,F0.95(6,8)=3.58,F0.05(6,8)=0.24,显然1.365,1.371,0.689介于F0.05(6,8)和F0.95(6,8)之间,因此可以接受原假设H0,即可以认为这批变压器的寿命服从双参数Weibull分布. 图1 分布直线拟合结果Fig.1 Fitting results of distribution line表3 应力水平Si下mi和ηi的最小二乘估计Table 3 Least squares estimators of miand ηi under stress levels Si 电压水平/KV^mib^i^ηi=exp(-b^i/^mi)35.41.203-6.544229.98242.42.018-6.66027.13946.71.843-4.94314.621 利用式(3)可计算出φ(S)与mη间的相关系数r=-0.991.在α=0.01显著性水平下,由于|r|=0.991>0.834 3=R0.01,故可认为假设A3成立.另外,对数特征寿命关于对数电压的散点图也表明lnηi与φ(Si)高度线性相关,其散点图如图2所示. 上述检验表明lnηi与φ(Si)高度线性相关,因此采用最小二乘估计法来估计加速模型中的系数β0与β1,其估计结果如表4所示. 图2 对数特征寿命关于对数电压的散点图Fig.2 The scatter diagram of log-characteristicvoltage for log-characteristic life表4 加速模型系数的估计值Table 4 The estimators of coefficients foracceleration model 加速模型系数β^0β^1加速模型系数估计值41.701-10.189 得到加速模型参数估计值后即可获得加速模型: (16) 正常应力水平S0下Weibull分布参数的估计为 正常应力水平S0下相应的可靠性指标估计结果如表5所示. 表5 正常应力水平下可靠性指标估计Table 5 Estimation of reliability indexes atnormal stress level 正常应力水平S0下可靠度函数为 R(t)=exp{-(t/5 344.545)1.689} (17) 其相应的可靠度曲线如图3所示. 图3 正常应力水平下可靠度曲线Fig.3 Reliability curve at the normal stress level 采用恒加试验方法,建立逆幂律-Weibull统计模型来实现高可靠度长寿命产品可靠性地快速评估,并利用最小二乘估计法对某型变压器在3个加速应力水平下的恒加试验数据进行可靠性统计分析,得结论: (1) 不同电压水平下Weibull分布具有共同的形状参数,表明在不同电压应力水平下变压器的失效机理不变的假定是合理的. (2) Weibull分布的对数特征寿命与对数电压间呈高度线性相关关系,其相关系数的绝对值为|r|=0.991,即Weibull分布的特征寿命与电压满足对数线性加速模型. (3) 得出了正常应力水平S0下Weibull分布的平均寿命,可靠度为0.8的可靠寿命t0.8,0,p(0.25,0.5,0.75)分位寿命的点估计,从相应的可靠度曲线图可对变压器的可靠寿命进行大致估计. 在快速评估高可靠度长寿命产品的可靠性研究方面,尽管取得了一些初步成果,但还存在不足,未来的研究工作可以从两个方面考虑: 一是为提高模型参数的估计精度,有必要考虑使用极大似然估计或贝叶斯估计法估计逆幂律-Weibull统计模型的未知参数. 二是仅考虑单应力恒加试验,然而产品的失效很可能是多种应力共同作用的结果;因此为提高高可靠度长寿命产品可靠性评估的精准度,有必要考虑综合应力加速寿命试验方法. [1] LEVADA S,MENEGHINI M,MENEGHESSO G,et al.Analysis of DC Current Accelerated Life Tests of Ganleds Using a Weibull-based Statistical Model[J].IEEE Trans-actions on Device and Materials Reliability,2005,5(4): 688-693 [2] 刘志全,李新立,遇今.长寿命航天器机构的加速寿命试验方法[J].中国空间科学技术,2008,28(4): 65-71 LIU Z Q,LI X L,YU J.Methods of Accelerated Life Tests for Long-life Spacecraft Mechanisms[J].Chinese Space Science and Technology,2008,28(4): 65-71 [3] 陈东生,宋永刚,徐强.基于工程可靠性分析的陀螺电机加速寿命试验设计[J].导弹与航天运载技术,2005 (6): 38-41 CHEN D S,SONG Y G,XU Q.Gyro Motor Accelerated Life Test Design Based on Engineering Reliability Analysis[J].Missiles and Space Vehicles,2005 (6): 38-41 [4] NELSON W B.Statistical Models,Test Plans and Data Analysis[J].John Wiley & Sons,2009(2):397-399 [5] 王炳兴.Weibull分布基于恒加寿命试验数据的统计分析[J].应用概率统计,2002,18(4): 413-418 WANG B X.Statistical Analysis for the Weibull Distri-bution Based on Constant Stress Accelerated Life Test Data[J].Chinese Journal of Applied Probability and Statistics,2002,18(4): 413-418 [6] WATKINS A J,JOHN A M.On Constant Stress Acce-lerated Life Tests Terminated by Type II Censoring at One of the Sress Levels[J].Journal of Statistical Planning and Inference,2008,38(3): 768-786 [7] 郑光玉,师义民.自适应逐步Ⅱ型混合截尾恒加寿命试验下广义指数分布的统计分析[J].应用概率统计,2013,29(4): 363-380 ZHENG G Y,SHI Y M.Statistical Analysis in Constant-Stress Accelerated Life Tests for Generalized Exponential Distribution Based on Adaptive Type-II Progressive Hybrid Censored Data[J].Chinese Journal of Applied Probability and Statistics,2013,29(4): 363-380 [8] 钱萍.航天电连接器综合应力加速寿命试验与统计分析的研究[D].杭州:浙江大学,2010 QIAN P.Research on Multiple Stress Accelerated Life Test and Statistical Analysis of Aerospace Electrical Connectors[D].Hangzhou:Zhejiang University,2010 [9] 陈文华,刘俊俊,潘骏,等.步进应力加速寿命试验方案优化设计理论与方法[J].机械工程学报,2010 (10): 182-187 CHEN W H,LIU J J,PAN J,et al.Theory and Method for Optimum Design of Accelerated Life Test Plan under Step-stress[J].Chinese Journal of Mechanical Engineering,2010 (10): 182-187 [10] 李新翼,郑海鹰.广义指数分布场合下简单步进应力加速寿命试验的最优设计[J].温州大学学报(自然科学版),2013,34(4): 12-17 LI X Y,ZHENG H Y.The Optimal Design for the Acce-lerated Life Tests of Simple Step-stress under Generalized Exponential Distributions[J].Journal of Wenzhou University (Natural Science Edition),2013,34(4): 12-17 [11] 茆诗松,王玲玲.加速寿命试验[M].北京: 科学出版社,2000 MAO S S,WANG L L.Accelerated Life Tests[M].Beijing: Science Press,2000 [12] 姜同敏.可靠性与寿命试验[M].北京: 国防工业出版社,2012 JIANG T M.Reliability and Life Tests[M].Beijing: National Defend Industy Press,2012 [13] 赵宜平,赵培信.R 统计软件在统计教学中的应用[J].重庆工商大学学报(自然科学版),2013,30(3): 74-76 ZHAO Y P,ZHAO P X.Application of R Statistics Software to Statistics Teaching[J].Journal of Chongqing Technology and Business University(Natural Science Edition),2013,30(3): 74-762.2 形状参数不变的假设检验

2.3 对数线性加速模型的假设检验

3 逆幂律-Weibull统计模型的参数估计
3.1 威布尔分布的参数估计

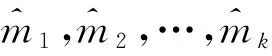
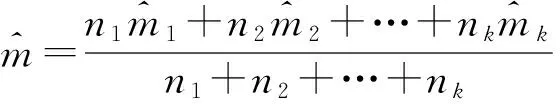
3.2 加速模型中β0和β1的估计




4 试验数据的可靠性统计分析

4.1 逆幂律-Weibull统计模型的检验

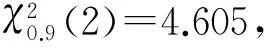
4.2 威布尔分布形状参数和尺度参数的估计
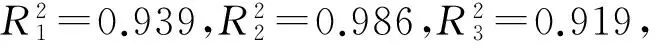
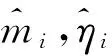
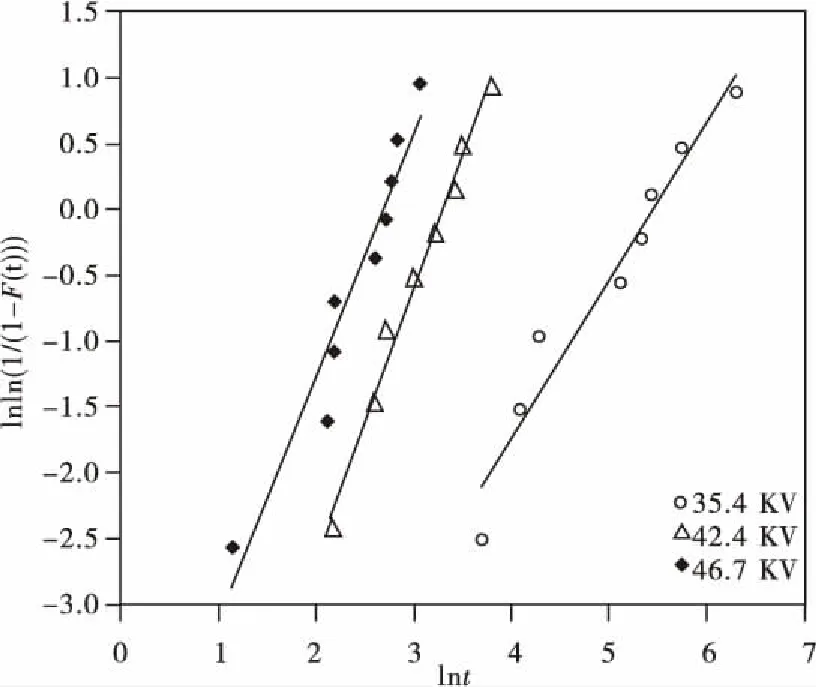
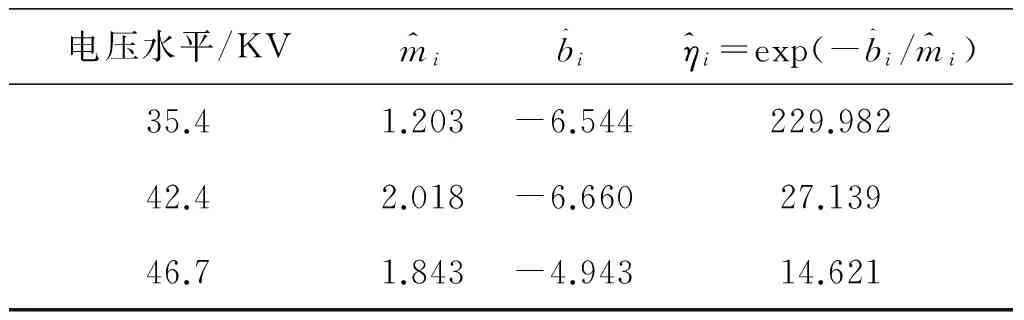
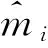
4.3 加速模型的估计


4.4 正常应力水平下可靠性指标的估计
5 结 论
