一种基于半监督学习的弹道目标识别方法∗

田西兰,郭法滨,赵洪立

(1.中国电子科技集团公司第三十八研究所,安徽合肥230088;2.孔径阵列与空间探测安徽省重点实验室,安徽合肥230088)

0 引言

弹道导弹因射程长、威力大、精度高和生存能力强等优势成为现代战争的一把利剑。对应地,弹道导弹攻防之间的博弈便决定了导弹防御系统存在非合作性强、决策时间短、监督式资源急缺等问题[1]。因助推段难以发现、再入段反应时间短等问题,弹道导弹目标识别问题往往集中在中段进行[2]。作为典型的高超声速目标,宽带识别方法因运动补偿困难、成像质量不佳等挑战,现役装备中应用相对较少,因此,本文致力于解决窄带中段弹道导弹反导识别问题,弹道目标为非合作的敌对目标,识别对象的目标特征数据事先很难被防御方获取,因此利用传统的监督式设计方法很难达到满意的识别结果。随着机器学习在各领域的广泛应用,利用先进的机器学习算法进行目标特征学习与分类识别器设计正成为雷达目标识别领域的研究热点。半监督学习算法利用少量的标定样本与大量的未标定样本进行样本空间搜索,所获取的半监督分类器能够实现对大规模真值未知数据的合理利用,进而在一定程度上缩减因非合作性强而导致的目标识别系统长研发周期[3]。本文针对反导目标识别中非合作性强、先验数据分布知识急缺的问题,设计了一种自动调整假设模型的半监督分类器。数据分析结果表明,该分类算法能明显缩减窄带弹道目标头体分辨识别任务中所需的标定样本的规模。

1 弹道目标RCS特性分析与特征提取

在中段,助推火箭关机,弹体分离,产生诱饵、碎片等伴飞物体,形成威胁目标群(一般又称头群)。该目标群在真空中按椭圆弹道惯性飞行至弹道最高点后朝地球下降;母舱、火箭助推器残骸、各种爆炸螺栓部件、碎片等则形成体群。中段飞行由于不受大气的阻力,头群、体群中的目标以近乎相同的方式飞行,但两者在形状及微运动特征上差异明显。研究表明[4-5],RCS序列为一种有效的进行窄带弹道目标分类识别的资源,图1为利用电磁仿真软件CST获得的RCS仿真图,其中,弹体由圆柱形刚体进行模拟,弹头由圆锥形刚体进行模拟。由图1可知,头群中的弹头目标RCS变化比较平稳,不具备周期性;体群中的弹体RCS变化较为剧烈,表现为一定的周期性。其原因在于弹头一般采取自旋等姿态控制措施,因此,相对入射电磁波的姿态变化范围较小;体群目标均不具姿态控制装置,形状相对较大,翻滚等运动会带来周期性的RCS幅值变化。

作为典型的时变系统,基于RCS序列的反导识别任务分段序贯完成。假设{x k|1≤k≤N}表示长度为N的目标RCS序列,本文提取以下典型的统计特征:

1)均值

该特征描述了RCS序列的位置特征参数,由于弹头目标尺寸较小且可能具有隐身特性,因此其RCS均值与弹体、末修舱等尺寸较大的目标相比偏小。

2)方差

该特征反映了样本的取值与其数学期望的偏离程度。由于弹头目标在飞行过程中可以进行姿态控制,因此其RCS起伏比较稳定,样本方差值相对较小,而对于弹体、碎片等目标,在空间呈现自由翻滚,因此其样本方差相对偏大。

图1 弹头、弹体RCS回波仿真图

3)众数

4)熵

对RCS序列进行傅里叶变换,并进行归一化操作求取其熵:

该特征表征了目标在能量谱上的分布情况。时域平稳的信号能量谱也较为集中,熵值较小;时域变化剧烈的信号能量谱分布较散,熵值也大。

5)切尾平均

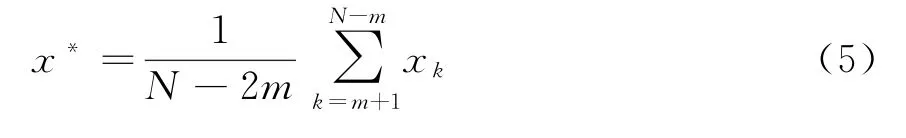
式中,m为序列两端截去的数据个数。对于RCS时间序列而言,截去样本两端的值,可以获得其在统计时间内的稳定的RCS,因此该特征反映了统计时间内目标RCS的稳态均值。

2 半监督分类器设计

目前多数的半监督学习方法往往对有限的已知样本和大量的未标定数据进行强的分布假设。最为常见的为“聚类假设”和“流形假设”两种。其中,聚类假设假定落在同一样本分布空间的两个样本也隶属于同一类;流形假设假定基于图表方法获得的预测标签在流形上分布平稳。针对“极小样本空间”的弹道目标识别任务,任何一种单一的模型假设都难以准确描述其样本空间分布,因此,本文采用多核学习框架,将“流形”假设模型引入到基于“聚类”假设的TSVM(Transductive SVM)框架中,从而实现对两个假设模型的统一处理。假定g(x)为决策函数,其优化问题表述如下:

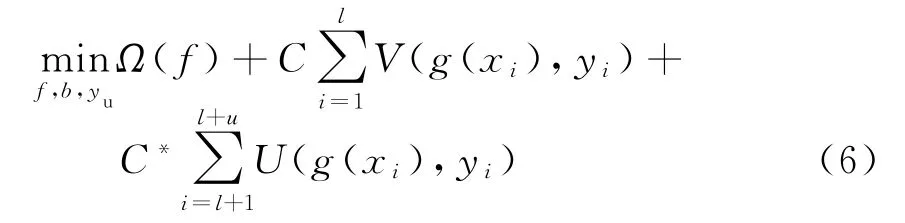
式中,g(x)=f(x)+b,f为希尔伯特空间的函数,b为实数标量,l为标定数据的规模,u为未标定数据的规模,V与U为对应的损失函数,yu为未标定样本的预测标签。

2.1 “流形假设”设计

“流形假设”由l+u维的拉普拉斯(Laplacian)核矩阵承载,定义为L=D-W,对其进行正则化处理可得L n=(I-D-1W)。式中,D为一对角矩阵并且满足

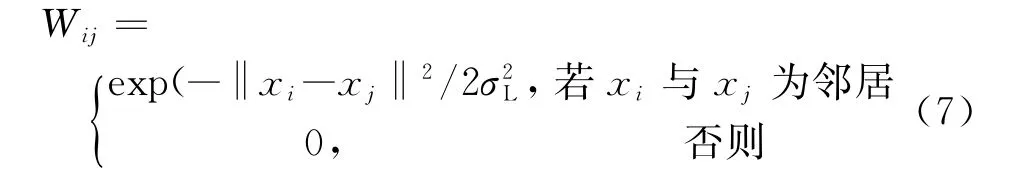
为相邻矩阵的权重。其构造方法如图2所示。

令决策函数g隶属于由核函数k生成的希尔伯特空间H,已被证明,Laplacian SVM所涉及的流形正则化问题可通过一个基于“重组核”的经典SVM问题解决,该“重组核”表示如下:

式中,k x=[k(x1,x),…,k(x l+u,x)]T。样本点的正则化云矩阵为为一个整数。

图2 拉普拉斯构造方法

2.2 自适应模型假设设计

多核学习(Multi-Kernel Learning,M KL)是一种融合不同源信息的有效方法[6]。基于式(6),假定未标定样本中正负类的分布与已知样本的分布状况相同,获得TSVM的多核学习框架TSVM-M KL[7]:

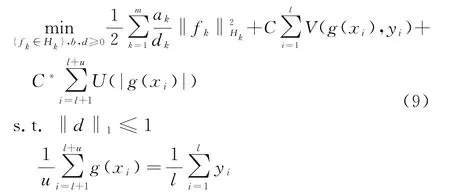
式中:m为核函数的个数;d k为当前核的权重,起到选择因子的作用,其值越大,该核矩阵所起的作用越大,为1时决策函数仅依赖于当前核,为0时不起作用;a k为正则因子;f k为第k个决策函数。此处约定t=0时,t/0=0,否则,其值为 ∞。TSVM-M KL的决策函数定义如下:

在解决上述优化问题时,设置平衡因子以约束大量未知样本中的正类、负类样本的分布情况。假设未知样本中,正类样本的比例为r,即应满足下式:

损失函数V和U均基于传统的铰链损失(Hinge Loss,HL)函数,其中,U(|z|)的一个可行性的定义可表示为

式中,R s(z)为铰链损失函数,即R s(z)=H1(z)-H s(z)。斜坡损失(Ramp Loss,RL)函数与截断铰链损失(Clipped Hinge Loss,CHL)函数表征如图3所示。将上述损失函数代入式(9):

该优化问题启用CCCP(Concave Convex Procedure)算法进行求解。详细算法表述如下:

TSVM-M KL二次规划的迭代过程:

设置初始估计值:d0,b0,f0k,t=0

重复如下过程:

计算v i,i=l+1,…,l+2u

求解下式的解d t+1,b t+1,f t+1k,k=1,…,m

直到满足收敛条件。

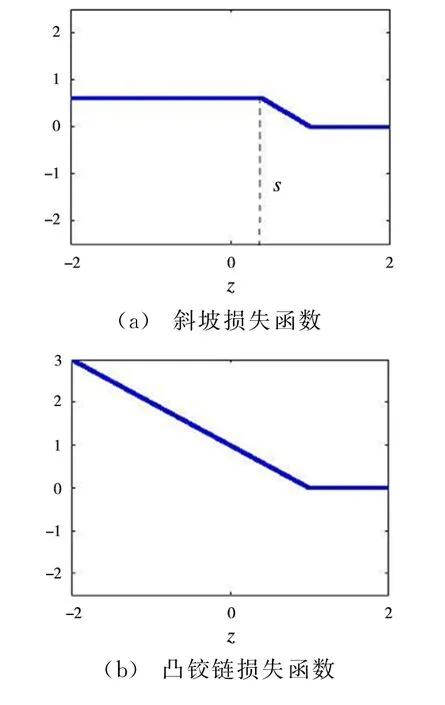
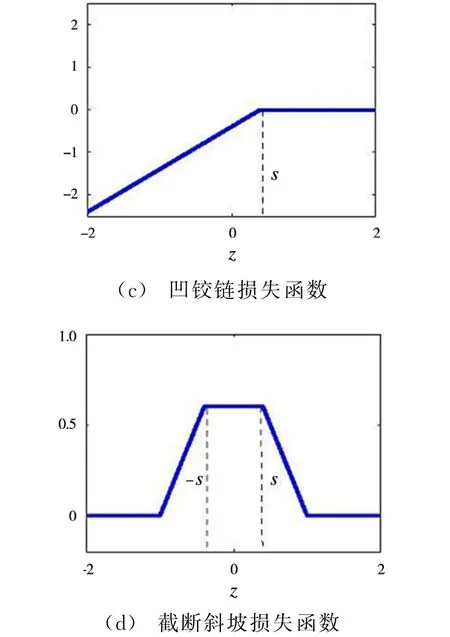
图3 损失函数

3 数据验证

本节以仿真数据为例,对所提算法进行验证。弹道目标识别的任务为区分弹头群、弹体群。其中,弹头群包括弹头、诱饵、末修仓、头体分离时的碎片等目标。弹头具有自旋稳定机构,角度变化比较稳定;弹体群目标包括各子级弹体残骸、级间分离时的碎片等目标。弹体不具有稳定机构,产生翻滚,角度变化剧烈。特征提取前对原始RCS序列进行了野值剔除。

观测数据中,头目标有60个样本,体目标有50个样本。为检验本文所提算法的有效性,实验分为两组,第一组抽取其中的10个样本作为标注样本(5个弹头、5个弹体),其余样本作为测试样本;第二组抽取其中的16个样本作为标注样本(8个弹头、8个弹体),其余样本作为测试样本。TSVM-MKL的试验设置为:拉普拉斯图谱的N取值为5;基本核函数均取为“Gaussian”型,核参数设置为0.25,0.5和1三个。与之对比的是基于常规SVM算法在上述数据上进行试验,采用5折交叉验证进行参数寻优,核函数同样设置为“Gaussian”型,核参数的搜索空间为logspace(-2,1,5),正则参数的搜索空间为logspace(-1,3,10),所得结果如表1所示。

表1 实测数据结果对比

由结果可知,SVM在如此小的标定样本下难以获得有效分类,即与随机分类器所得结果一致,而本节所提的TSVM-MKL在极小样本下依然能够获得满足工程需求的分类准确率。

4 结束语

弹道导弹目标识别技术面临的一项重大挑战是样本数据难以标定、样本库建立困难。针对该问题,本文设计了一种半监督式分类器,一方面,可以综合利用反导实战中累积的未标定数据;另一方面,由于训练过程中扩大了样本的“探索”与“利用”范围,从而使得在极小标定样本规模的情况下,仍能获得较好的分类性能。实测数据验证表明,该算法适合于工程应用。

[1]李陆军,丁建江,吕金建,等.弹道导弹目标特性研究[J].飞航导弹,2015(6):34-39.

[2]张平定,孙佳佳,童创明,等.弹道中段目标雷达综合识别研究[J].微波学报,2015,31(2):20-23.

[3]吴剑旗,田西兰.一种基于半监督学习的窄带雷达目标识别系统[J].中国电子科学研究院学报,2015,10(1):49-53.

[4]魏文博,蔡红军.基于支持向量机的窄带雷达弹道导弹目标识别技术[J].电子科技,2016,29(6):75-78.

[5]崔雄文,田西兰.一种融合聚类和自相关的RCS周期估计算法[J].雷达科学与技术,2016,14(6):614-618.

[6]RAKOTOMAMONJY A,BACH F R,CANU S,et al.Simple MKL[J].Journal of Machine Learning Research,2008,9(3):2491-2521.

[7]TIAN X,GASSO G,CANU S.A Multiple Kernel Framework for Inductive Semi-Supervised SVM Learning[J].Neurocomputing,2012,90(8):46-58.