新课程理念下职业高中数学教学

孙志军

职高学生有特定的学习心理特点，就是职高学生的学习起点普遍较低，他们的思维水平普遍不高.这是职高学生不愿意自主学习的重要原因.在教学过程中，教师要针对职高学生的心理特点引导学生自主学习.教师要引导学生掌握科学的思维方式，培养学生的自主学习能力，使学生积极探索科学文化知识.

一、将数学教学内容直观化

高职学生来源不同.有些学生的数学理论知识不完善、解决问题的能力不强，不能理解过于抽象的知识.如果教师不顾这些学生的思维水平，一味开展抽象化的理论教学活动，就会导致这些学生在学习中受到挫折，不能理解知识，最终放弃学习.在教学过程中，教师要尽可能运用直观的教学方式.

例如，在讲“渐开线的概念”时，教师可以引导学生做实验：把一根没有弹性的绳子绕在圆盘上，在绳子的外端上系一只笔，让绳子被笔拉紧.然后让绳子绕圆做切线运动，看绳子最终能绘制出一条怎样的线.学生发现应用这样的方法能绘制出一条有规律的渐开曲线.在实验中，学生能初步理解渐开线的轨迹似乎与圆的半径、圆心与铅笔的距离、与沿着圆切的角度有关系.在学生初步理解渐开线后，教师可以引导学生调节实验参数，观看渐开线的变化.学生在实验过程中慢慢了解了渐开线是一种绕着圆、圆的半径延伸出来的直径做切线运动获得的轨迹，渐开线的生成轨迹与圆的半径、延伸直线的距离、沿着圆切的角度有密切的关系.

在教学过程中，教师可以运用多媒体视频、虚拟实验、实体实验的方法引导学生学习知识.直观的教学方式，能使学生更容易理解知识，从而提高学习效率.

二、鼓励学生自主发掘知识

在学生初步了解数学概念后，教师要引导学生学习抽象知识.这个过程是学生发掘知识、理解知识的重要過程.

例如，教师可以结合上述实验引导学生画出一幅抽象的数学图形.有些学生不懂得如何把具体的案例抽象化，教师可以提出问题，引导学生思考：这个实验，需要了解的知识是什么呢？经过思考，学生认为这个实验是要探索渐开线方程的轨迹.教师

追问：如何应用数学知识描述轨迹呢？学生经过思考，认为可以应用平面几何图形与坐标图来呈现轨迹路线.于是学生把圆、

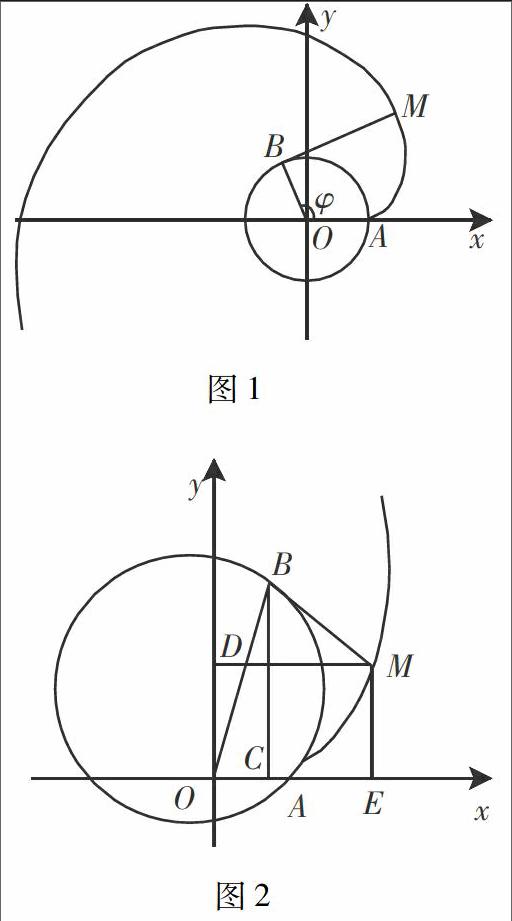
直线、渐开线等几何图形放到坐标图上探讨.教师提出问题：如何探讨渐开线与圆、直线的参数关系呢？经过思考，学生认为应当应用字母符号来描述每个几何事物的关系，便于探究几何问题变化的规律.学生绘出如图1.教师提出问题：如果要探讨渐开线的方程，需要探讨什么问题？经过思考，学生了解到这次要探讨的知识是渐开线的轨迹，即渐开线曲线坐标与相关参数的变化，即要探索的问题为每一点M，它的坐标变化与其他参数的关系.当学生能从抽象的角度找到需要探索的数学问题及影响数学问题的因素时，就能结合既有的学习经验开始探索知识.

当学生从具象的角度初步理解知识后，教师要引导学生学会运用抽象思维的方法把具象的问题数学化，使学生运用数学方法探讨问题.学生只有学会运用这样的方法探索问题，才能理解需要探索的数学知识及找到探索知识的方向.

三、帮助学生掌握科学思想

当学生理解了需要探索的知识后，教师要引导学生学会运用科学的方法思考问题.学生只有掌握了数学思想这种利器，才能解决各类问题.

例如，在建立了图1这一平面直角坐标系，并把需要探讨的问题呈现在图象中时，教师可以提出问题，引导学生思考：M（x，y）与哪些因素有关？学生要结合既有的知识理解这一问题.这是一个解析几何的问题.这个问题，既与几何知识有关，又与几何的坐标生成有关.教师要引导学生结合学过的知识绘制辅助线，并探讨渐开线的生成与哪些几何图形有关.经过思考，学生绘制辅助图形得到如图2.

在教学过程中，教师要引导学生思考：在遇到问题的时候，为什么要运用绘图的方法来解决问题？学生发现，当初思考如何构建渐开线方程时，找不到学习的方向，是因为这个问题太抽象、太复杂.因此，学生绘制图形，利用图形来理解这个问题，找到了解决问题的方法.教师的提问给了学生提示，使学生意识到遇到抽象的、复杂的问题时，可以把数学问题转化成图形，从而利用图形找到解题的切入点.

四、引导学生联想拓展

在学生应用一个切入点解决问题后，教师要引导学生思考：能不能发散思维，把知识点与知识点结合起来，找到新的切入点？

教师要引导学生学会寻找知识点和知识点的相似性，利用性质相似的特点来转化问题，找到新的解题切入点.当学生从多种角度看问题时，思考问题的视野就会变得开阔.

总之，在教学过程中，教师要用直观化的方式帮助学生理解知识，使学生理解自己需要探索哪些知识；引导学生学会把具象的问题变成抽象的问题，使学生能以数学的方式来思考问题；引导学生掌握数学思想，使学生熟练掌握解决问题的利器；引导学生把知识点与知识点结合起来，以多元化的角度看待问题.只有这样，才能提高学生的思维水平，促使学生自主学习数学知识.endprint