初中数学教学中培养学生的思维能力

张于婧

初中阶段是学生数学思维发展的“关键期”.初中生的思维特点主要表现为：（1）由于年龄特征及知识水平的局限，学生的形象思维有待培养，主要靠直观思维思考问题.对于具体、形象的问题，学生的思维比较活跃；对于抽象的问题，学生一时找不到解释，便茫然无措；习惯于某种思维模式，遇到问题，一味期望能套用某个现成公式.这些都反映了思维的变通性和应变能力较差.（2）对概念、公式、定理等满足于形式上的理解、记忆，往往忽视其来龙去脉和知识的系统性，对数量之间的逻辑关系缺乏整体的认识；对各种数学思想和方法之间的共性与个性缺乏了解.这样，学生在学习过程中无法逐步建立和完善思维的整体结构，影响了对新知识的理解.（3）不善于从多角度、多方面、多维度去思考问题.在教学实践中，教师要有目的、有计划地针对学生的思维特点进行严格的思维训练，利用他们成熟前可塑性人的特点（主要表现为多思、多疑、多问等），精心创设合适的问题情境，通过“问题解决”“质疑反思”等教学形式，帮助学生形成良好的思维品质.

一、通过一题多解，培养思维的发散性

一题多解是培养学生的发散思维的重要方法.在教学中，教师要引导学生善于从旧的模式中解脱出来，针对一个对象能从多种角度观察，针对一个信息能向多个方向发散，针对一个题目能提出不同解法.一题多解，能够让学生对一个问题从不同角度、不同方向进行探索和思考，开拓思路，从而培养学生的思维发散能力.

二、通过转化，培养思维的灵活性

转化就是将复杂问题转化成简单问题，将抽象问题转化成具体问题，将未知问题转化成已知问题.数学来源于生活，又为生活服务.很多生活中的实际问题，都可进行用数学知识来解决，而这些问题往往都是综合性数学问题.在解决这些问题时，常常用到方程、函数、几何图形的知识，有时图形的问题需要转化为方程解决，有时在解方程时又要结合图形来分析.

例如，在讲“一元一次不等式的实际应用”时，我提出这样的问题：在科学与艺术知识竞赛中，共有20道题，对于每一道题，答对得10分，答错或不答扣5分，总得分不少于80分者能通过预选赛.育才中学有25名学生通过了预选赛，通过者至少要答对多少道题？有哪些可能情形？这道题就用到了转化思想.因为题目中出现了“总得分不少于80分”的不等关系，所以要将实际问题转化为不等式的问题来解决.

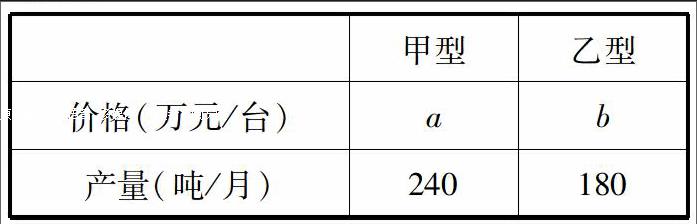
又如，某公司为了提倡低碳经济，节约能源，决定购买10台节省能源的新机器，现有甲乙两种型号的设备，其中每台的价格和工作量如下表.经调查：购买一台甲型设备比购买一台乙型设备多2万元，购买2台甲型设备比购买3台乙型设备少6万元.（1）求a，b的值.（2）经预算：该公司购买的节能设备的资金不超过110万元，请列式解答有几种购买的方案可供选择.这道题的第一问显然是转化成解方程组的问题来解决.而第二问有“不超过110”这个不等关系，于是可以转化为不等式的問题来解决.

三、反思探索，培养思维的批判性

在教学中，教师可选准时机，适当出错，制造思维冲突，诱发灵感，使学生分清错误类型，搞清问题之所在，增强防止错误的免疫力.教师要引导学生反思，促使他们从新的角度、多层次、多侧面地对问题及解决问题的思维过程进行分析与思考，以深化学生对概念、定理、法则和公式的理解，揭示问题的本质.反思会使解题过程更趋于完善和合理，克服思维定式负迁移的影响，有利于培养学生思维的批判性.

例如，在讲“一元一次方程”时，我给出如下随堂练习：解下列方程：（1）4-x=3（2-x）；（2）-2（x-1）=4；（3）5（x-1）=2-3（x+1）；（4）6x-7（1-x）=6.反思：练习共4个，采取抽签形式，活跃课堂气氛，每组完成一道题，各派一个代表上黑板板演.为了调动学生的积极性，在学生完成此题之后，我给学生一分钟的时间检查黑板上同学的错误，并上台批改，使学生在一种比较活跃的氛围中解决各种问题.最后师生共同评价这些题的解题思路.整堂课都是学生自己在解决问题，教师只是引导者.

综上所述，在初中数学教学中培养学生的思维能力是一个长期的过程，不是一日之功，任务艰巨复杂，需要教师不断探索.endprint