基于力密度矩阵和平衡矩阵的张拉整体结构找形方法
2018-01-19冯晓东张佳丹周倩倩
冯晓东 张佳丹 周倩倩
(绍兴文理学院 土木工程学院,浙江 绍兴 312000)
0 引言
张拉整体结构是一种轻质、网状、智能的空间结构体系,这类结构一般由若干个受压的杆元和受拉的索元组成.根据杆元接触与否可将张拉整体结构分为两类:一类张拉整体结构(杆元不接触)和二类张拉整体结构(杆元接触).在任何外力作用之前,由于受拉索元中自应力的存在(包括重力),使得整个结构体系能够保持自平衡状态.正是由于这类智能结构存在的一系列潜在优点(刚度可协调性、主动阻尼共振、形态可控性),自20世纪50年代后,“张拉整体”的概念已经深入贯穿于整个科学和工程领域,包括建筑、土木、航空航天、智能机器人、生物等学科.众所周知,在生物力学领域,张拉整体模型已被视为研究细胞骨架力学特性的合适模型[1-2].如图1所示的细胞骨架,实际上是由三种不同的聚合物纤维组成的复杂结构:微丝(受拉)、微管(受压)和中间丝(连接微丝和微管).然而由于这些纤维网络的几何和拓扑形态极为复杂,导致目前现有的张拉整体模型[3-4]不能很好地解决所有问题.因此,在寻找和设计复杂的、非对称的以及自由形态的张拉整体结构体系方面,仍有大量工作可以深入研究.
在过去的半个多世纪,已经有不少学者把注意力集中在张拉整体结构找形上,其中包括对规则和不规则张拉整体结构找形的研究.目前,对于此类研究主要有:力密度法,用于张力结构找形及应用[5];动力松弛法的提出及非线性问题的解决[6];改进的力密度数值找形计算方法[7-9];利用有限单元法解决结构找形问题[10-11];遗传算法在张拉整体结构找形中的应用[12];自应力多模态下数值找形方法[13-15];利用平衡方程和几何相容方程的结合解决找形问题[16].

微丝 微管 中间丝图1 一个活细胞细胞骨架的聚合物网络[1]
大部分现有的找形方法都必须事先假定一系列繁琐的条件.例如,将力密度系数作为符号变量[17];为简化找形步骤假定结构的整体对称性[18];在动力松弛法中,事先假定若干个单元的长度[6,17].事实上,这些信息在找形之前并不都是那么容易确定的.因此,这类方法对于解决复杂的、非对称的张拉整体结构的找形仍很困难. 本文提出了一种新颖的数值分析方法,目的在于解决一类和二类张拉整体结构的找形问题.它是将结构体系的力密度矩阵和平衡矩阵分别采用谱分解和奇异值分解后进行双向循环迭代,最后根据力密度矩阵和平衡矩阵的最小秩亏条件,求出满足要求的节点坐标和力密度,通过相当小数量的迭代即可获得任意稳定态(切线刚度矩阵为正定矩阵)或超稳定态(几何刚度矩阵为正定矩阵)张拉整体结构的自由形态.目前其他已有的找形方法,需要事先严格定义或假定张拉整体结构的初始节点坐标、单元长度、材料特性、几何对称性以及力密度矩阵的半正定性等一系列条件,而文本所呈现的方法不需要这些繁琐的假定,只需要确定结构的空间维数、单元类型以及节点间的几何拓扑关系(节点和单元的关联性),这也正是本文相比于其他找形方法的优势所在.
1 力密度找形法及相应的秩亏条件
1.1 基本假定
众所周知,张拉整体结构的找形过程与索网结构非常类似,这是因为它们都具有相同的基本假定(最后两个只适用于张拉整体结构),如下列出:
a.结构的几何拓扑关系已知,并且结构的几何形状只能通过相应的节点坐标来确定;
b.单元之间均为铰接;
c.不考虑外力作用并且忽略结构自重;
d.不考虑局部或整体弯曲变形;
e.没有耗散力作用于结构体系.
1.2 张拉整体结构的自平衡方程
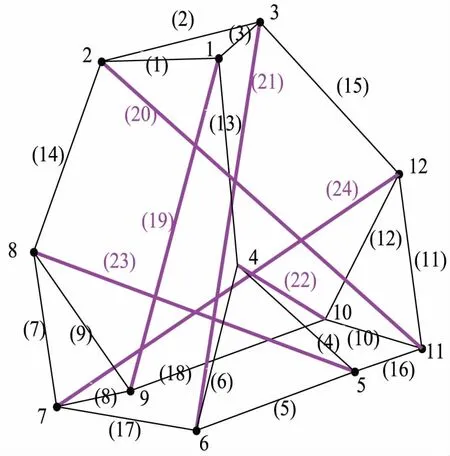
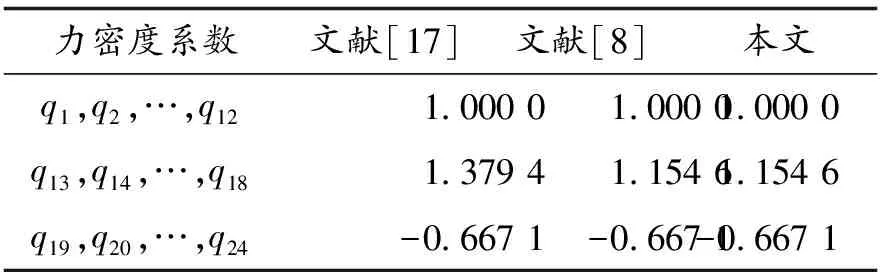
对于一个有b个单元、n个自由节点、nf个固定节点的d维张拉整体结构(d=2或3),它的几何拓扑关系可以用关联矩阵CS∈Rb×(n+nf)表示[19-20].假定连接单元k两端的节点号分别为i和j(i (1) 由于固定节点在数字标记顺序上可优先于自由节点,因此可将关联矩阵CS分为如下两部分: (2) 式中:C∈Rb×n为自由节点与单元之间的关联矩阵;Cf∈Rb×nf为固定节点与单元之间的关联矩阵. 令x,y,z(∈Rn)和xf,yf,zf(∈Rnf)分别代表自由节点和固定节点在x-,y-和z-方向的节点坐标向量.并且定义q={q1,q2,…,qb}T∈Rb为力密度系数矩阵,其中每个组成部分为该单元的力fk和单元长度lk的比值,qk=fk/lk(k=1,2,…,b).因此,整个结构体系的力密度矩阵Q∈Rb×b可以写成如下形式: Q=diag(q). (3) 由此铰接结构所有自由节点在每个方向上的平衡方程组可以写成如下形式: CTQCx+CTQCfxf=px; (4.1) CTQCy+CTQCfyf=py; (4.2) CTQCz+CTQCfzf=pz. (4.3) 式中:px,py,pz(∈Rn)分别代表x-,y-和z-方向作用在自由节点上的外力向量. 为简化方程,定义矩阵E∈Rn×n和Ef∈Rn×nf如下: E=CTQC; (5.1) Ef=CTQCf. (5.2) 由式(5.1)可知,对于任意一个张拉整体结构,矩阵E总是一个对称的奇异方阵,这是因为矩阵任意一列或行的元素之和都等于0[19]. 考虑张拉整体结构本身的特性(无固定节点),并且在忽略外力和自重的情况下,整个结构体系可以被看作为一个空间自由体系,它的几何形状可由相应的节点坐标确定.因此,式(4.1)~式(5.2)可以写成如下形式: Ex=0; (6.1) Ey=0; (6.2) Ez=0. (6.3) 为简化起见,可将式(6.1)~(6.3)合并整合为 (7) 将式(5.1)代入式(6.1)~式(6.3),合并可得张拉整体结构的自平衡方程: (8) 式中:A∈Rdn×b为张拉整体结构的平衡矩阵. 由上述可知,矩阵E和A分别代表了张拉整体结构的力密度矩阵和平衡矩阵.因此,对于一个存在自应力的d维张拉整体结构,必须满足两个必要但不充分的秩亏条件[19]. 第一个秩亏条件是关于半正定矩阵E,如下: nE=n-rE=n-rank(E)≥d+1. (9) 式中nE为矩阵E的秩亏. 第二个秩亏条件是关于平衡矩阵A,同时也是式(8)无解的必要条件,如下: s=rA=rank(A) (10) 这个秩亏条件能够保证结构的自应力模态数s=b-rA≥1.独立机构位移模态数为m=dn-rA.[21]值得注意的是,由于张拉整体结构是自平衡体系,因此结构的独立机构位移模态数包括刚体位移模态数和无穷小机构位移模态数两部分.其中无穷小机构位移模态数mim按下式计算: mim=m-rb; (11) (12) 式中:m为独立机构位移模态数;rb为刚体位移模态数;d为张拉整体结构的空间维数. 不同于现有的大部分找形方法,本文所提出的方法不需要事先假定单元长度以及结构的几何对称性等条件.换言之,本方法只需要确定结构的空间维数、单元类型以及节点间的几何拓扑关系,便可确定张拉整体结构的最终形态,实现找形的目的. 为了确定每个单元的力密度系数,根据单元受力情况,如下定义矢量q0: (13) ; (14) (15) 将力密度矩阵E进行特征值分解,如下: E=HΛHT; (16) HHT=In. (17) 式中:H∈Rn×n为正交矩阵,并且其第i列hi∈Rn为矩阵E的特征向量基;In∈Rn×n为单位矩阵;Λ∈Rn×n为对角矩阵,并且其对角线上的元素为相应的特征值,即Λii=λi. 矩阵H的特征向量hi则对应于矩阵Λ的特征值λi. 根据上述分解可知,力密度矩阵E特征值为零的个数等于其零空间的维数[22].此时,若定义k为矩阵E特征值小于或等于零的个数,则有如下两种情况需要考虑. 图2 自由形态张拉整体结构找形流程图 (18) (19) Chi=0; (20) det|ld(ld)T|=0; (21) (22) 式中:ld为d维空间(假定d=3)中d个特征向量任意组合而成的b个单元的长度向量. 此外,本阶段尚需要确定张拉整体结构的切线刚度矩阵KT,其表达式如下[7,26]: ⊗E. (23) 式中:KE为张拉整体结构的线刚度矩阵;KG为与自应力模态有关的几何刚度矩阵;e为结构各单元材料的杨氏模量(矢量);a为结构各单元材料的横截面面积(矢量);l0为结构各单元的初始长度(矢量);I∈R3×3为单位矩阵;⊗为张量积. 如果切线刚度矩阵是正定的,则整个结构体系在刚体位移被限制的情况下将是稳定的.也就是说,对于任意一个非平凡变动d,矩阵KT的二次型是正定的: dT(KT)d>0; (24) 或 eig(KT)=eig(KG)= (25) 式中:rb为式(12)中定义的独立的刚体机构数目. 结合上述两种情况可知,在空间三维张拉整体结构的找形过程中,最有效的方案就是在前四组特征向量基(分别相应于前四个最小的特征值)中选择三组可能的特征向量,将这些特征值通过本方法逐步减小直至为零,最终求出相应的节点坐标矩阵,使得结构体系达到平衡状态,即 (26) 一旦相应的节点坐标被确定,就可以将这些已知值从式(18)代入式(8)中.为了求解式(8),可将平衡矩阵A进行奇异值分解: A=UVWT; (27) (28) (29) μ1≥μ2≥…≥μb≥0. (30) 式中:U∈Rdn×dn和W∈Rb×b均为正交矩阵;V∈Rdn×b为由矩阵A的非负奇异值组成的对角矩阵,其奇异值大小按式(30)排列. 在迭代找形步骤中,同参数k在矩阵E的谱分解过程中类似,此时对于s同样存在以下两种情况. 2.2.1 平衡态(s=1) 由于张拉整体结构的力密度和机构的矢量空间基,是通过计算平衡矩阵零空间得到的[27],因此在这种情况下,矩阵U和矩阵W应有如下形式的零空间: ; (31) (32) 式中:m∈Rdn为m个无穷小机构所组成的矢量. 定义机构矩阵M∈Rdn×(dn-rA)如下: (33) 此时,结合s=b-rA=1,可将式(32)写成如下形式: (34) 如果矢量q1与q0有相同的符号关系,即 sign(q1)≡sign(q0), 则矢量q1为满足齐次方程(8)的唯一自应力模态. 2.2.2 非平衡态(s=0) 在这种情况下,结构内部不存在自应力模态,式(27)中定义的矩阵A不存在零空间.换言之,V中A的右奇异值μb不等于零.因此,式(8)不存在关于力密度系数矢量q的非零解.此时如果将矩阵W的右奇异矢量基wb(对应于矩阵V中最小的右奇异值μb)作为近似的q,则矢量q1与q0不一定会有相同的符号关系.为了解决这个问题,本文采用的找形方法必须逐一试验矩阵W中的所有列,直到寻找到某个wj(j=b,b-1,…,1),使得其中的所有元素与q0有相同的符号关系,即:sign(wj)≡sign(q0).此时,矢量wj可以直接选取作为近似的q.经过上述步骤,整个找形过程寻找出了合适的q,使得 Aq≈0. (35) 综上所述,本文所提出的找形方法的主要思路就是将式(7)和式(8)进行双向循环迭代,直至满足式(14)和式(15)所述的两个秩亏条件.需要指出的是,对于某个给定的张拉整体结构,根据本方法所求得的力密度系数矢量q不是唯一的.换言之,对于相同的关联矩阵C和同样符号的q0,可能存在其他的矢量q满足条件. 根据张拉整体结构必须满足自平衡的条件,本文将如下定义的不平衡力矢量υf∈Rdn作为评估计算结果精度的指标: υf=Aq. (36) 或者可将不平衡力矢量分别在x-,y-和z-方向上投影: υx=Ex; (37) υy=Ey; (38) υz=Ez. (39) 引入Euclidean范数,设计误差κ可以表述为: Tol=10-10. (40) 本文要求设计误差κ必须控制在10-10以内. 本节将通过二个数值算例(包括一类和二类张拉整体结构)来证实本方法的有效性和适用性.研究结果表明,本文所提出的找形方法对于分析解决稳定形态和超稳定形态的张拉整体结构是非常适用的. 图3所示为一个由6杆18索组成的三维截顶四面体张拉整体结构.先前有学者在研究这个结构时,强制设定结构的所有杆元等长,同时结构的所有索元也等长.例如在非线性找形方法[17]和动力松弛法[6]中都曾做过这样的假定.然而,这一类限制条件在本方法中是不需要的,而仅需要输入的信息为关联矩阵C、结构的空间维数以及各单元的类型.与二维张拉整体结构相同,根据本文所提出的找形方法,自动分配初始力密度矢量如下: 图3 三维截顶四面体结构 (41) 最终得到的归一化力密度系数矢量(相对于杆1的力密度)如表1所示,与文献[8]相符.与此同时,本结构可能存在的两个不同的索元长度也被找到并且记录于表2中.图4展示了本结构在无指定节点坐标下的几何形态. 整个找形过程经过8次迭代后收敛,且设计误差κ=1.281 0×10-11 表1 三维截顶四面体结构的力密度系数 力密度系数文献[17]文献[8]本文q1,q2,…,q121 00001 00001 0000q13,q14,…,q181 37941 15461 1546q19,q20,…,q24-0 6671-0 6671-0 6671 表2 截顶四面体结构找形过程中各参数的迭代明细 迭代次数q1,q2,…,q12q13,q14,…,q18q19,q20,…,q24l1-12c/lsl13-18c/lsκ10 2116950 242427-0 1351530 4010490 5088301 5965×10-220 2118400 244480-0 1309350 4040450 5016178 0669×10-430 2118460 244584-0 1307210 4042810 5012774 0456×10-540 2118460 244589-0 1307100 4042930 5012602 0282×10-650 2118460 244589-0 1307100 4042940 5012591 0168×10-760 2118460 244589-0 1307100 4042940 5012595 0972×10-970 2118460 244589-0 1307100 4042940 5012592 5553×10-1080 2118460 244589-0 1307100 4042940 5012591 2810×10-11 图4 无指定节点坐标下得到的截顶四面体结构的几何形态 图6所示为一个由7杆19索组成的三维十二面体张拉整体结构.经计算最终得到的归一化力密度系数矢量(相对于杆1的力密度)为: 找形过程仅经过一次迭代即达到收敛,且设计误差 κ=4.914 9×10-16 满足条件. 图7展示了本结构在无指定节点坐标下的几何形态.在限制该结构的6个刚体位移模态(rb=6)后,其最终的结构形态存在一个自应力模态(s=1)和零个无穷小机构位移模态(mim=0),这也意味着该结构体系为静不定但动定结构. 图5 截顶四面体结构在迭代找形过程中的收敛曲线 如上所述,相比其他找形方法,本文所提出的方法不要求力密度矩阵E为半正定矩阵.在本例中,力密度矩阵E有三个负特征值,即为半负定矩阵;这就表明此结构不是超稳定的,因此需要确保所有的无穷小机构位移模态已被自应力模态所强化.为了简化计算量,假定所有单元有相同的轴向刚度eiai=5,根据式(23)计算该结构的切线刚度,其中力密度系数矩阵按式(42)取值.忽略6个刚体位移模态所对应的前6个零特征值,最终所得切线刚度矩阵KT的非零特征值均列于表3中.可以看出最小的特征值为0.044 0,这表明该结构的确是稳定的. 图6 三维十二面体结构 图7 无指定节点坐标下得到的十二面体结构的几何形态 表3 三维十二面体结构切线刚度矩阵的特征值 特征值特征值λ10 0440λ104 2452λ21 2759λ114 6603λ31 2787λ126 1446λ41 3225λ1314 5749λ51 9081λ1414 9212λ62 4737λ1519 2174λ73 1477λ1619 3417λ83 8934λ1738 4478λ94 0035λ1878 4237 在原始力密度找形方法的基础上,本文将结构几何拓扑理论和矩阵分析理论应用于张拉整体结构的找形过程,并提出了综合考虑几何拓扑、结构刚度、稳定性、设计误差等诸多因素的张拉整体结构的找形方法. 找形过程由计算机编制程序实现,不用反复试算,大大缩短了找形周期.该找形方法利用矩阵分析理论将结构的力密度矩阵和平衡矩阵两者之间的关联反映出来.而且,通过计算结构切线刚度矩阵的特征值来判断结构体系的稳定类型,结合不同类型的张拉整体结构模型和相关软件对具体实例进行计算和分析,表明本文所提出的找形方法对于分析解决稳定形态和超稳定形态的张拉整体结构是非常适用的. [1]INGBER D E. The architecture of life[J]. Scientific American,1998,278(1):48-57. [2]INGBER D E,TENSEGRITY I. Cell structure and hierarchical systems biology[J]. Journal of cell science,2003,116:1157-1173. [3]LAZOPOULOSK A. Stability of an elastic tensegrity structure[J]. Acta mechanica,2005,179(1-2):1-10. [4]PIRENTIS A P, LAZOPOULOS K A. On the singularities of a constrained (incompressible-like) tensegrity-cytoskeleton model under equitriaxial loading[J]. International Journal of Solids and Structures,2010,47(6):759-767. [5]SCHEKH J. The force density method for form finding and computation of general networks [J]. Computer Methods in Applied Mechanics and Engineering,1974,3(2):115-134. [6]MOTRO R, NAJARI S, JOUANNA P. Static and dynamic analysis of tensegrity systems[C]∥Proceedings of the international symposium on shell and spatial structures,computational aspects. Springer,1986:270-279. [7]ZHANG J Y, OHSAKI M. Adaptive force density method for form-finding problem of tensegrity structures [J]. International Journal of Solids and Structures,2006,43(18-19):5658-5673. [8]ESTRADA G, BUNGARTZ H, MOHRDIECK C. Numerical form-finding of tensegrity structures [J]. International Journal of Solids and Structures,2006,43(22-23):6855-6868. [9]TRAN H C, LEE J. Advanced form-finding of tensegrity structures [J]. Computers & Structures,2010,88(3-4):237-246. [10]PAGITZ M, JUR J M M. Tensegrity frameworks: static analysis review [J]. Mechanism and Machine Theory,2008,43(7):859-881. [11]卢成江,吴知丰,赵洪斌.非线性有限元法分析张拉整体结构初始形态[J].沈阳建筑大学学报(自然科学版),2007,23(6):900-904. [12]XU X, LUO Y. Form-finding of nonregular tensegrities using a gentic algorithm [J]. Mechanics Research Communications,2010,37(1):85-91. [13]TRAN H C, LEE J. Form-finding of tensegrity structures with multiple states of self-stress [J]. Acta Mechanica,2011,222(1-2):131-147. [14]LEE S, LEE J. Form-finding of tensegrity structures with arbitrary strut and cable members [J]. International Journal of Mechanical Science,2014,85(8):55-62. [15]ZHANG L Y, LI Y, CAO Y P, et al. Stiffness matrix based form-finding method of tensegrity structures [J]. Engineering Structures,2014,58(7):36-48. [16]KOOHESTANI K, GUEST S. A new approach to the analytical and numerical form-finding of tensegrity structures [J]. International Journal of Solids and Structures,2013,50(19):2995-3007. [17]TIBERT A G, PELLEGRINO S. Review of form-finding methods for tensegrity structures [J]. International Journal of Space Structure,2003,18(4):209-223. [18]MASIC M, SKELTON R, GILL P. Algebraic tensegrity form-finding [J]. International Journal of Solids and Structures,2005,42(16-17):4833-4858. [19]MOTRO R. Tensegrity: Structural Systems for the Future [M]. London: Kogan Page,2003. [20]陈志华,王小盾,刘锡良.张拉整体结构的力密度法找形分析[J].建筑结构学报,1999,20(5):29-35. [21]PELLEGRINO S, CALLADINE C R. Matrix analysis of statically and kinematically indeterminate frameworks[J]. International Journal of Solids and Structures,1986,22(4):409-428. [22]MEYER C D. Matrix analysis and applied linear algebra [M].Philadelphia:SIAM,2000. [23]CONNELLY R. Rigidity and energy [J]. Inventiones Mathematicae,1982,66(1):11-33. [24]CONNELLY R. TERRELL M.Globally rigid symmetric tensegrities [J]. Structural Topology,1995,21:59-78. [25]CONNELLY R. Generic global rigidity [J]. Discrete & Computational Geometry,2005,33(4):549-563. [26]OHSAKI M, ZHANG J Y. Stability conditions of prestressed pin-jointed structures [J]. International Journal of Nonlinear Mechanics,2006,41(10):1109-1117. [27]PELLEGRINOS. Structural computations with the singular value decomposition of the equilibrium matrix [J]. International Journal of Space Structure,1993,30(21):3025-3035.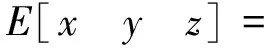
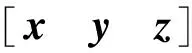
1.3 两个必要的秩亏条件
2 基于矩阵分析的找形步骤
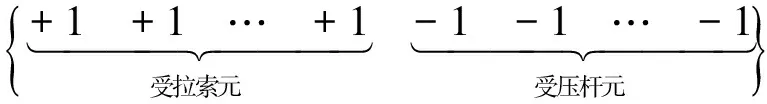
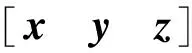
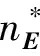
2.1 力密度矩阵的特征值分解
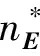

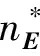
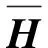
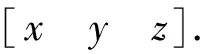
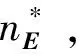
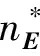
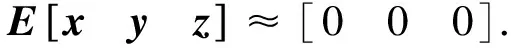
2.2 平衡矩阵的奇异值分解
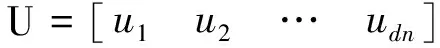
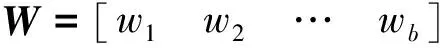
2.3 设计误差评估
3 算例
3.1 截顶四面体
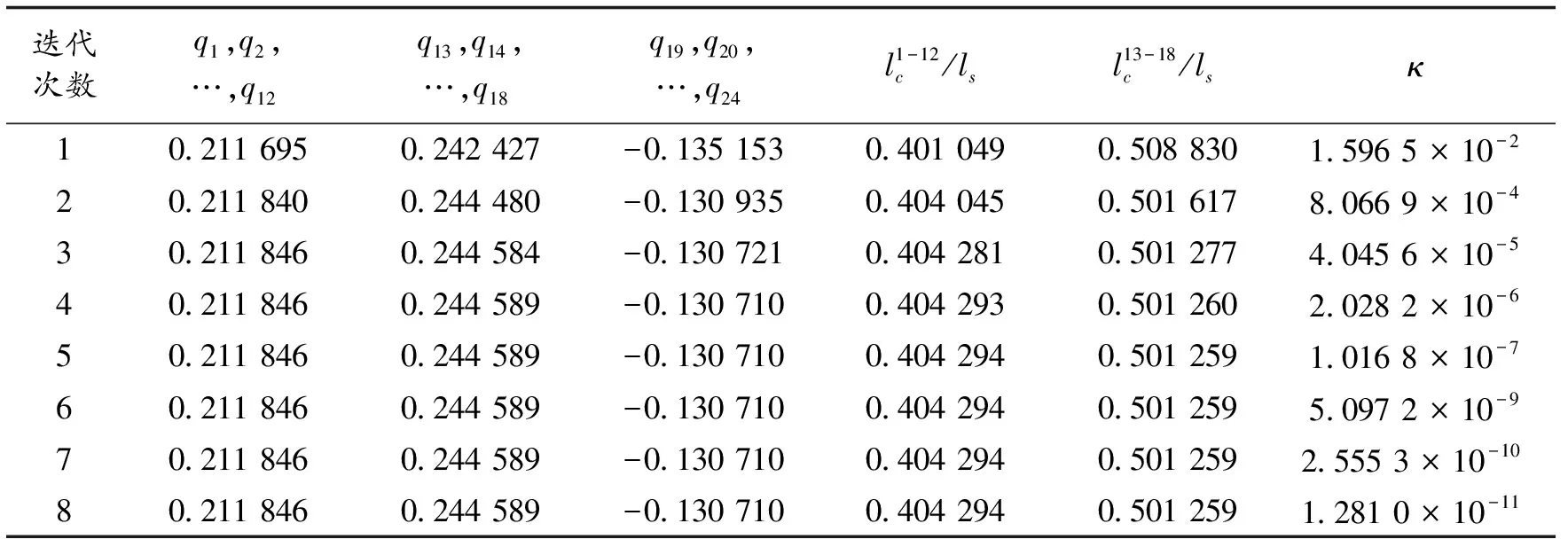
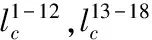
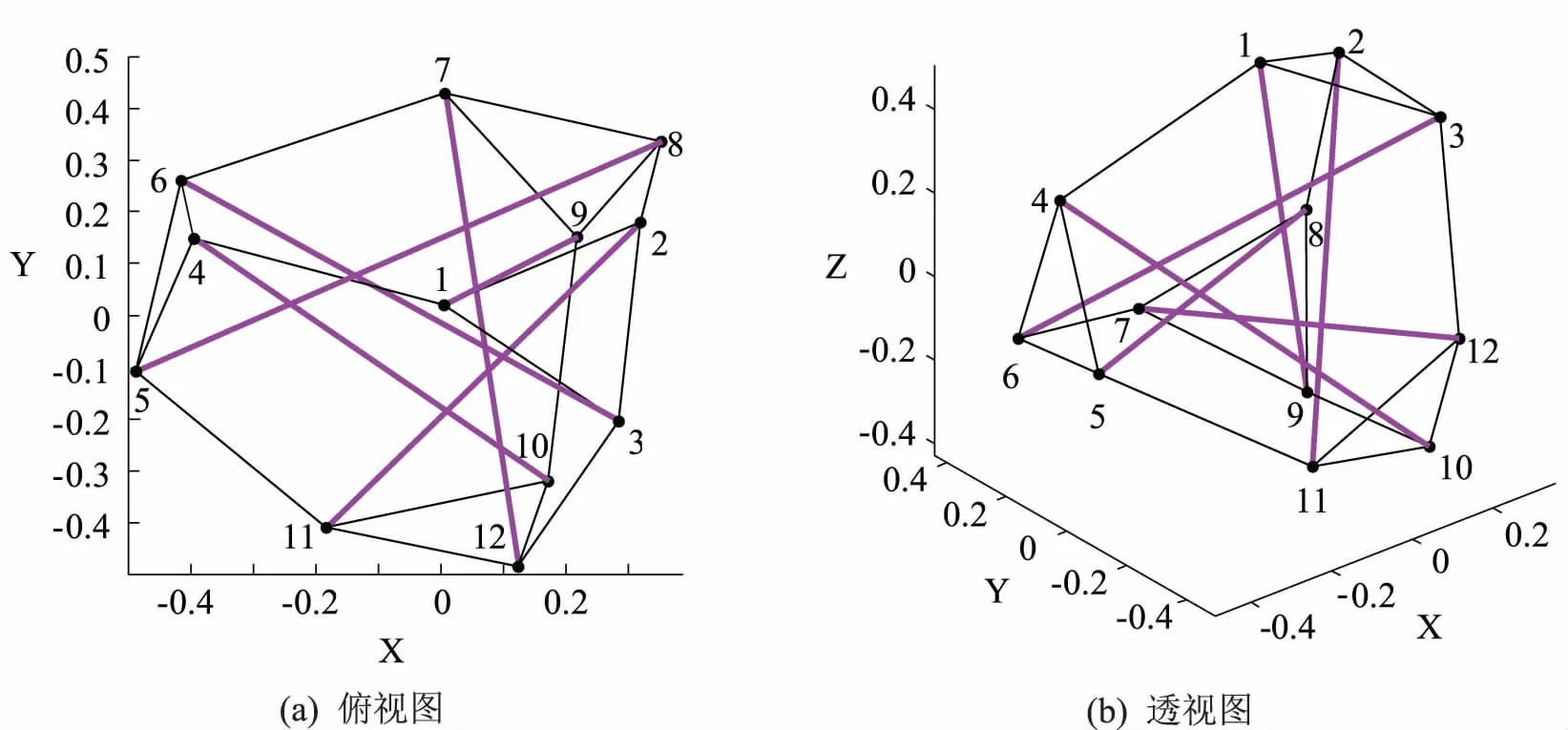
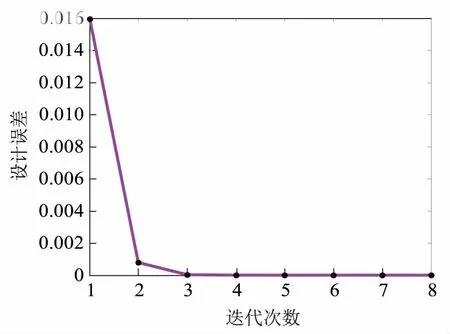
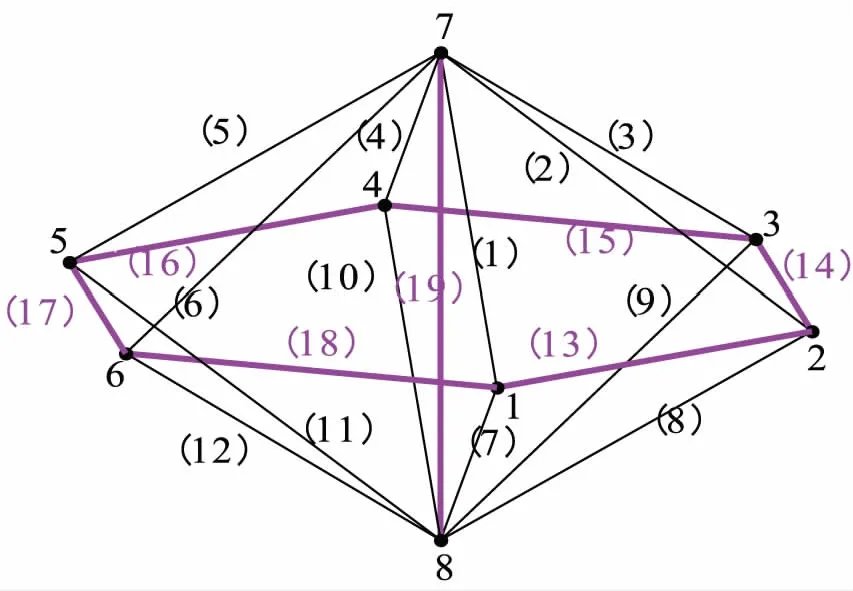
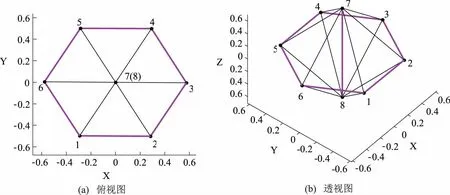
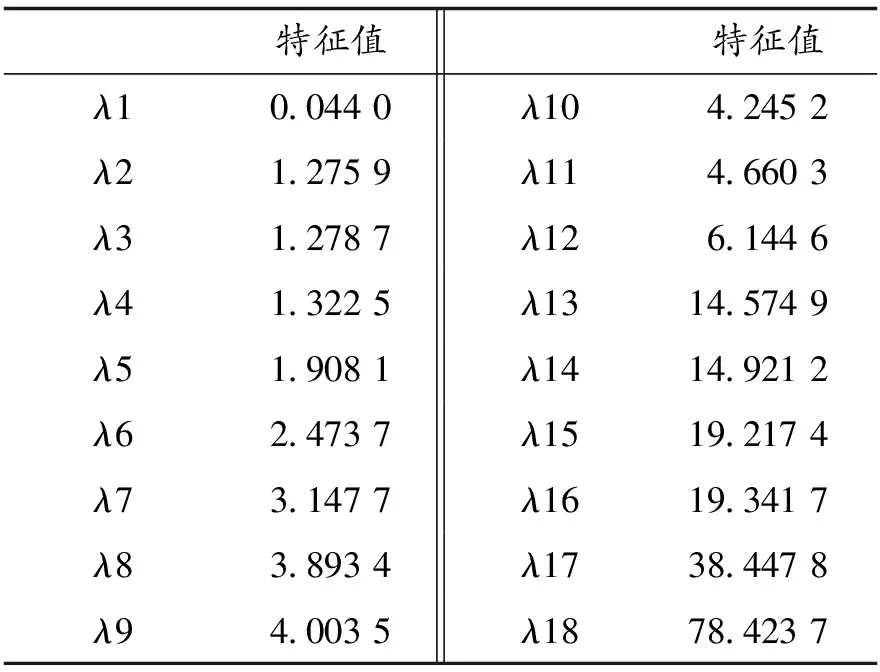
3.2 十二面体
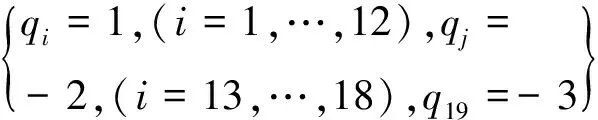
4 结论
