进相试验中水轮发电机进相安全域的计算
2018-01-19闫迎晏桂林郝剑波任章鳌
闫迎,晏桂林,郝剑波,任章鳌
(国网湖南省电力公司电力科学研究院,湖南长沙410007)
发电机进相运行作为一种欠励磁运行方式,通过调节励磁电流的大小可以改变从电网吸收的无功功率,达到调节电网电压的目的〔1〕。但是在进相方式下,随着发电机吸收电网无功功率的增多,机组静态稳定性降低,机端电压下降,定子电流上升,这些变化对机组的安全都有不利影响。因此,对发电机安全进相深度的确定必须通过现场试验测试的方法实现〔2-3〕。
近年来随着水电机组单机容量及总装机容量的不断增加,利用水轮发电机进相调压愈来愈受到电网的重视。但是相对于隐极机组来说,水轮机组的进相过程更加复杂,尤其是不同负荷下的极限功角互不相同,试验中若盲目地通过监视功角等参数的变化趋势来决定进相是否终止,会为机组运行带来很大的风险,严重者甚至会导致发电机失磁失步等事故发生〔4-5〕。因此试验前若能快速简单地对水轮发电机的安全进相深度进行估算,并提前了解进相限制因素,可为试验中无功功率调节和试验监视提供依据, 避免事故的发生〔6-7〕。
文中从进相试验的需要出发,介绍了一种利用数值计算手段确定水轮发电机进相安全域的方法,该方法在保证机组静态稳定的同时,综合考虑多种约束条件对进相的影响。以某一机组进相试验为例,计算与试验结果对比表明该方法计算精度较高,能够为进相试验的控制提供数据支持,有重要应用意义。
1 水轮发电机进相稳定边界方程的建立
水轮发电机在进相运行中,静态稳定是最关键的问题。一般情况下,发电机常与升压变压器以单元接线的方式与无穷大系统相连,因此这里以图1所示的某一单机无穷大系统模型对机组的稳定问题进行说明,该系统的向量图如图2所示。

图1 单机无穷大系统阻抗模型

图2 单机无穷大系统相量
图中,Eq、Ug、Ut分别为发电机空载感应电动势、机端电压、升压变高压侧电压、电网电压;Xd、Xq分别为发电机直轴和交轴电抗;Xt为升压变短路电抗;Xs为无穷大系统电抗,两者统称外部阻抗;δ为Eq与Us的夹角,称为系统功角,α为Eq与Us的夹角,称为发变组功角。除δ和α外上述各参数均折算为相同基准值下的标幺值。
在不考虑励磁调节器作用下,根据图2中的相量关系,可以得到该系统输出功率 Ps和 Qs分别为〔8〕:
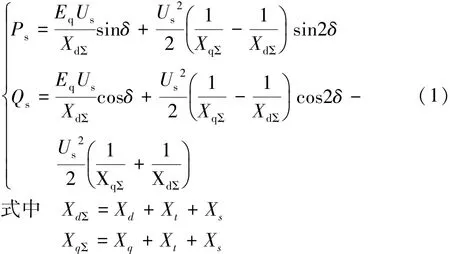
为分析方便,这里做如下替代,令

则式 (1)可写为:

在假设励磁电压和系统电压不变的情况下,从式 (2)可以看出该系统的输出功率由功角δ唯一确定,且在稳定边界处有dPs/dδ=0,即:
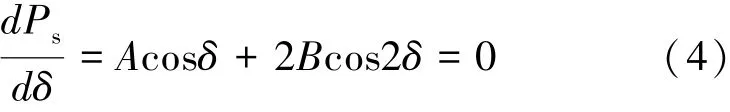
对于式(2)—(4),各式均为单一未知量δ的函数,因此首先将式 (3)代入式 (4)并整理得到:
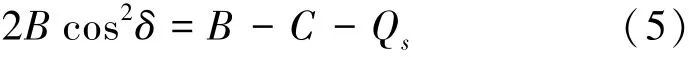
随后将式 (2)代入式 (3)整理得到:

联立式 (5)和式 (6),整理后得到如下表达式:

若将式 (2)代入式 (4),整理后还可得到:

对于水轮发电机来说,由于B≠0,因此将式(8)两边平方并继续整理后还可得到如下表达式:

由式 (7)和式 (9)可以看出,在已知系统电压Us和有功功率Ps等条件下,两式均为单一未知量Qs或sin2δ的一元三次方程,分别求解两个方程即可得到在静态稳定范围内该系统的极限输出无功功率和极限系统功角。因此这里将式 (7)和式(9)称为水轮发电机组在系统侧的静态稳定边界方程〔9-10〕。另外,结合发电机的励磁曲线,由还可求出边界点处的励磁电流,这对于试验时失步点的观察判断具有十分重要的作用。
事实上,水轮发电机在静稳边界处的最大进相深度也可以用静稳圆来描述,但是功率圆只是反映了发电机本身吸收极限无功功率随有功功率出力和机端电压的变化趋势,未能考虑系统电压、外部阻抗等条件对机组进相的影响。而静态稳定边界方程更多的是分析发电机组—电网系统的进相情况,与功率圆相比,优点在于考虑到了电网条件对进相运行的限制,使得进相更加安全。
2 进相边界对机组安全的适应性分析
进相试验中只要控制系统输出无功功率及系统功角不超过式 (7)和式 (9)确定的边界值,理论上可以保证机组运行在稳定安全状态。但是在计算过程中,方程中所取参数很难实时反应电网设备的真实状态,这就导致机组在临近计算边界区域进相运行时,将会面临着不可预知的风险,因此开展进相边界下的机组安全性分析很有必要〔11〕。
2.1 系统电抗对进相安全的影响
在发电机进相试验中,实际上无法在电网中找到一条与图1中Us对应的理想母线,因此试验中通常近似地把电厂内升压变高压侧母线当做无穷大电网,用Ut代替Us对电网进行监测,忽略系统电抗Xs对进相试验的影响。即在计算过程中做如下变动:
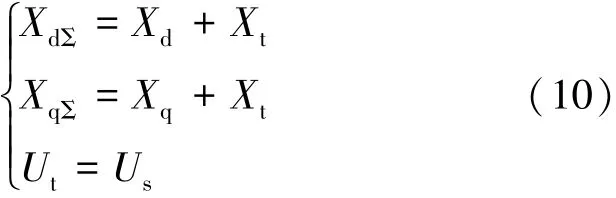

图3 不同系统电抗下发电机进相边界曲线
图3是某发电机组在不同的系统电抗下进相运行时,进相边界随有功功率出力的变化曲线。图中Xs=0为系统进相计算边界,也是发变组边界,同时还是试验监测边界,Xs≠0为系统进相实际边界。从图中可以明显看出,当Xs远小于Xt时,计算边界接近与实际边界,当试验中控制发变组功角或无功功率输出不超过计算边界范围时,整个系统将会运行在稳定范围内;但当Xs相对Xt不能完全忽略时,计算边界与实际边界之间会存在一个比较明显的偏差,当试验中监视到的发变组功角或无功功率输出尚未超出计算边界时,系统功角或无功功率可能早已超出系统实际稳定边界,导致机组提前进入失稳区。
2.2 系统电压对进相安全的影响
进相试验中系统电压会随着进相深度的增加而有所降低,鉴于试验中系统电压的下降幅度很小,且也很难预测该电压的降落趋势,因此计算中一般忽略该电压降落,近似认为系统电压Us=1。

图4 不同系统电压下发电机进相边界曲线
图4是某机组在不同的系统电压水平下进相边界随有功功率出力的变化曲线。从图中可以看出,系统电压对极限无功功率有较大的影响,而对极限功角的影响较小,具体表现在系统电压越高,进相极限深度越大,极限功角越小,因此假定系统电压稳定不变的发电机组计算进相能力要略大于系统电压轻微下降下的实际进相能力。因此在试验中当以计算出的极限无功功率为依据控制机组进相时,也会增加发电机进相失稳的风险。
2.3 同步电抗对进相安全的影响
在发电机运行过程中,受磁场饱和的影响,同步阻抗值要略小于不饱和设计值,且磁场越饱和,同步阻抗值越小。在发电机进相过程中,同步电抗的饱和程度时很难实时监测并确定的,因此计算中采用的发电机同步电抗参数通常为不饱和设计值。
设发电机饱和电抗分别为 X′d=kdXd,X′q=kqXq,考虑到d轴饱和程度一般要大于q轴,因此有kd<kq<1。
图5是某机组在不同的磁场饱和程度下进相边界随有功功率出力的变化曲线。由图可见,在相同的工况条件下,采用电抗不饱和设计值计算出的进相极限无功功率绝对值及极限功角均最小,这说明利用发电机不饱和参数计算出的极限无功功率和功角比较保守,以此为依据进行进相深度的控制可以保障机组的运行安全。

图5 不同同步电抗下发电机进相边界曲线
3 水轮发电机进相运行深度的校核
综上分析可知,静稳计算边界对于发电机组的进相运行只是一种理想状态,在边界点处很难保证机组仍在稳定范围内。另外,即使保证发电机组不会失去稳定,也无法保证发电机定子电流、机端电压等指标仍满足运行要求,因此为保障机组安全,必须对计算边界进行适当约束条件下的校核。
3.1 考虑功角约束条件
发电机进相试验过程中,一般要求最大允许功角 (Eq与Ut间的夹角)与极限功角相比,要留有15°~20°的裕度,这实际上是在保证机组具有足够的静态稳定系数的同时,也减小了边界计算误差对系统运行稳定的影响。
已知发电机有功功率出力Ps和系统电压Ut,根据相量图 (2)可知,进相过程中最大允许进相深度Qs与其对应的功角δ满足如下关系
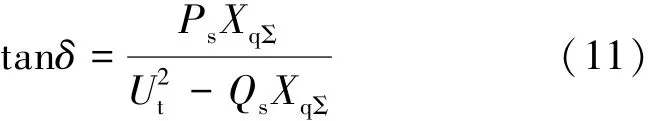
设此工况下的极限功角和极限无功功率计算值分别为 δ°、Q°,δ相对 δ°的裕度为 Δδ。根据式(11)可得以发电机功角为约束条件的进相深度表达式为:
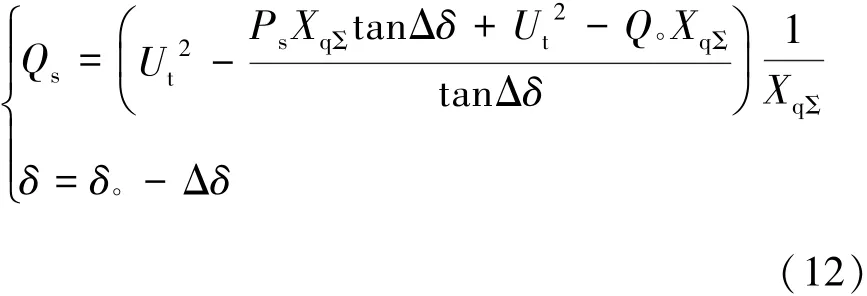
则发电机机端电流为

发电机机端无功功率Qg和电压Ug分别为

3.2 考虑机端电流约束条件
进相试验中发电机机端电流会随着进相深度的增加而增大,试验中控制机端电流不超过额定值IN。已知有功功率出力Ps和系统电压Us,可得升压变高压侧容量Ss和进相无功功率Qs分别为

则发电机机端无功功率Qg为

3.3 考虑机端电压约束条件
进相试验中发电机机端电压会随着进相深度的增加而减小,试验中控制机端电压不低于额定电压的90%,即Ug≥0.9。已知有功功率出力Ps和系统电压Us,根据图 (2)中的相量关系,有

可求得机端电压控制下的最大进相深度Qs为

3.4 考虑厂用电压约束条件
电厂内厂用电压Uc一般由发电机机端提供,进相中机端电压的降低会造成厂用电压的降低,试验中一般控制Uc不低于额定厂用电压的95%。已知发电机机端电压Ug,厂用变压器短路阻抗Xc,厂用负荷Pc+jQc,考虑到厂用变压器容量一般较小,这里忽略变压器上的损耗,则得到厂用电压Uc的计算式为
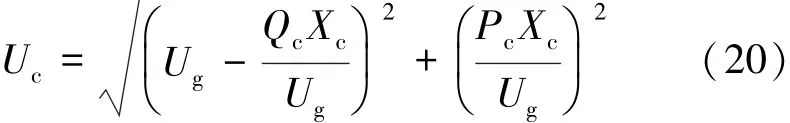
3.5 考虑端部温升约束条件
发电机定子端部温升对发电机的进相运行也有限制作用。端部温升主要由复杂的端部漏磁决定,鉴于对其很难精确建模,建议在试验中密切监视。
3.6 进相深度校核流程
在发电机有功功率出力Ps和系统电压Us给定的条件下,以发电机静稳边界为基础,考虑功角裕度、机端电流和机端电压等约束条件,发电机安全进相范围的校核流程如图6所示。

图6 进相安全域校核流程
4 算例分析
以湖南省内某300 MW水轮发电机系统为例,计算和实测了不同工况下的机组进相运行数据,结果见表1。表中功角为Eq与Ut的夹角,进相无功功率均为发电机机端输出功率,各重要设备相关参数:1)发电机:SN=333 MVA,PN=300 MW,UN=18 kV,Xd=1.15,Xq=0.7; 2) 升压变:SN=360 MVA,UN=550/18 kV,Xt=14%。 试验在不同时间段,两种不同的电网电压水平下进行,试验中控制电压分别不低于525 kV和530 kV。

表1 某300 MW水轮发电机组进相运行数据
对表中数据进行分析可以看出,根据计算方法得到的发电机进相运行数据与现场实测数据相比有很高的一致性,特别是最大安全进相深度等关键参数的误差均未超过6%,而且通过计算方法推测到的机组进相限制因素与试验验证的限制因素是一致的。这说明文中计算方法能够为进相试验的开展提供数据支持,对于发电机安全进相范围的预测、进相限制因素的确定、试验前临时保护的设置、进相过程中电气量变化趋势的判断等具有积极意义。
另外还可看出,有功功率出力对发电机的进相运行有很大影响:有功功率出力越大,安全进相深度越小,因此要想增加发电机的无功功率输出,可以适当减小发电机的有功功率出力;系统电压对发电机进相深度的影响次之,系统电压较高时发电机进相深度相对较大,但其功角变化不大。
5 结论
根据发电机静态稳定条件,建立了水轮发电机的静态稳定方程,得到了不同有功功率出力和系统电压条件下的机组进相运行边界。通过分析不同设备参数下的进相边界稳定情况,发现当计算中忽略系统电抗或系统电压降落时,以计算边界为参考进行试验监控时容易增加机组失稳的风险,相反采用发电机不饱和阻抗值代替实际阻抗进行边界计算并以此为依据进行进相深度控制时可保障发电机的安全运行。为提高计算边界的适用性,文中考虑功角裕度、机端电压、定子电流等约束条件的进相边界校核满足了试验中机组运行安全的需要。虽然根据文中计算方法得到的水轮发电机进相运行值与实测值相比具有不可避免的误差,但是两者还是具有较好的一致性,数据误差也能够满足工程应用中对精度的需要,这都表明文中计算方法可以为进相试验的开展提供数据支持,具有实际使用价值。
〔1〕汤涌,仲悟之,孙华东,等.电力系统电压稳定机理研究 〔J〕.电网技术,2010,34(4):24-29.
〔2〕严伟,陈俊,沈全荣.大型隐极发电机进相运行的探讨 〔J〕.电力系统自动化,2007,31(2):94-97.
〔3〕陈群,袁庆来,陈讯,等.当前国内开展进相运行的意义及存在的问题 〔J〕.大电机技术,2000(2):14-18.
〔4〕刘喜泉,谢燕军,陈小明,等.水轮发电机低励限制与失磁保护整定配合研究与试验 〔J〕.大电机技术,2016(1):59-61.
〔5〕伍常林,李永林,熊续平.一起机组突然深度进相故障的分析及处理 〔J〕.华东电力,2010,38(11):1830-1831.
〔6〕王成亮,王宏华.大型同步发电机进相运行动模试验设计 〔J〕.电测与仪表,2016,53(2):118-124.
〔7〕曹侃,王涛,忻俊慧.同步发电机进相能速快速估算方法 〔J〕.中国电力,2014,47(1):108-111.
〔8〕李发海,朱东起.电机学 〔M〕.北京:科学出版社,2001:259-265.
〔9〕王勇.水轮同步发电电动机静态稳定运行曲线绘制及应用〔J〕.大电机技术, 2015(4):34-37.
〔10〕郭景斌,单周平.水轮发电机静态稳定应用分析方法 〔J〕.大电机技术,2000(4):23-26.
〔11〕李志强,何凤军,晁晖,等.进相试验中水轮同步发电机静态稳定限制的数值分析 〔J〕.电机与控制学报,2011,15(12):89-95.
