基于FPGA状态机非对称高斯拟合寻峰算法的研究

2018-01-18郭晓彤杨秋翔

电子设计工程 2018年1期

郭晓彤，杨秋翔

（中北大学软件学院，山西太原030051）

光纤光栅（Fiber Bragg Grating，FBG）传感器是近几年来使用频率高且应用广泛的一种新型光纤传感器。由于它具有耐腐蚀，耐高温，可靠性高，安全性强等诸多优越特性，很容易被制作成检测气体浓度、温度以及压力等物理量信息的传感器[1-2]。通过感测外界物理量的变化，与光谱解调仪采集得到的反射谱中心波长的移位量进行判断，实现对大型设备结构状态的实时监测[3-5]。由于中心波长的移位量对应的是反射谱峰值位置的变化，所以快速准确的寻找峰值点是检测的关键。在FBG数据采集过程中，光纤光栅波长信号会存在较大噪声的干扰，造成了在峰值点附近会出现波动现象，导致了反射光谱的不对称[6-7]。而使用传统的寻峰算法[8-11]，如直接寻峰法、高斯拟合法等解决此类问题时，需要忽略波动现象，从而会产生较大的误差，导致精确度下降；人工智能算法解决此类问题时，会导致时间运行成本过高。

针对上述问题，Wang等提出了基于Steger寻峰算法[12]，Liu等提出了自适应半峰检测寻峰算法[13]，其它等提出的相关算法可参见文献[14-16]。基于Steger寻峰算法，引入超高斯模型完成不对称寻峰，但超高斯函数参数选择使此方法精度受到影响；自适应半峰检测寻峰算法，通过引入实验经验值，对非对称峰值进行补偿，但此经验值的确定存在误差，导致寻峰精度受到影响。为了弥补上述算法的不足，本文提出一种基于FPGA状态机的非对称高斯拟合寻峰算法。本算法采用FPGA超强的可编程并行计算来对光纤光栅波长信号进行滤波寻峰处理，状态机为FPGA中的灵魂核心部分，基于状态机的转换过程中对数据处理完毕后再通过对波形的判断及峰值的修正完成寻峰过程，避免了存储空间的浪费，同时在速度和精度上，都得到了提升。

图1 原始反射光谱图

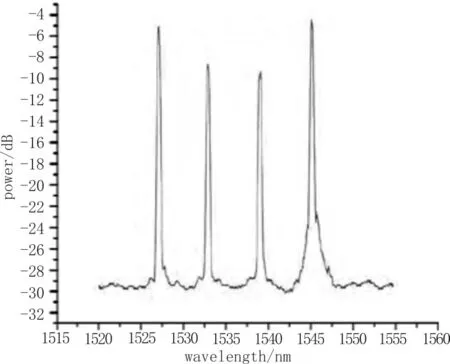
图2 滤波后反射光谱图

1 算法概述及原理

1.1 算法概述

由于外界环境及信号采集过程中所夹杂的噪声影响，使得反射谱的峰值点发生偏移，很大程度上影响了寻峰的精度，所以要先对采集得到的离散数据进行滤波处理后再寻峰。算法过程为：对采集得到的数字信号滤波，完成预处理部分；然后通过状态机的转换，将去噪后的波形数据调节阈值进行分割，粗略估计峰值所在位置范围；对此范围的波形数字进行判断，若为对称波形，峰值则直接为高斯拟合后的峰值；反之则进行非对称高斯拟合，对高斯拟合所得到的峰值进行补偿修正。此算法基于FPGA状态机对预处理后的数据再次进行处理，然后寻峰。不仅提高了速度并且弥补了以往常见寻峰算法对于非对称波形的忽略问题，提高了算法的精度。

1.2 寻峰算法

1.2.1 滤波预处理

为了消除设备自身以及外界环境所产生的噪声影响，首先采用巴特沃斯低通滤波对采集的数字信号做预处理。如图1所示，分别为原始波形图和滤波处理后的波形图。

1.2.2 峰值区域分割采集模块

本模块的作用为采集滤波后的有效数据。由图1可见，通过巴特沃斯滤波处理后的数据可以有效的剔除“毛刺”等噪声干扰，得到一条较为平滑的曲线（见图2），此时若直接进行寻峰计算，数据量大，且其中有大部分数据均为冗余数据，会对数据的处理以及系统运行的速度带来不必要的工作量，占用资源，降低速度。所以进行数据筛选是非常必要的一步，此处可设定阈值，小于该点则不予考虑，完成初步的分峰截幅。通过大量的实验比对调整后得出，此处设置的阈值为信号中心波长的75%处值，可有效滤除掉少量杂波跟噪声。

1.2.3 峰值数据检测模块

本模块的作用为采集峰值处的数据，为此后的寻峰算法提供更为可靠有效的数据信息。具体过程为上升、下降、错误三态之间进行相互转化，并在FPGA系统内分别设计了用于记录保持稳定同状态的数据，上升态的起始位置数据以及下降态终止位置数据的寄存器，将其存入数组a[n]中。

具体过程为：

首先与预处理后的数据逐个进行对比，若当前数据大于设置的阈值且前一数据小于阈值，将此数据计入起始位置寄存器中，转入下一数据；若当前数据大于阈值且大于前一数据，则开始进入波形的上升态，将当前数据与上一数据进行差值比较，差值范围设定为K（K值为大量实验数据对比后所确定的值），若差值小于等于K，则此时保持同状态；若差值大于K，则认为此时波形发生波动，进行下一步判断：当差值为正时，若前一状态为下降态，则下一状态为错误态，否则仍为上升态；若差值为负，则转换为下降态。若当前数据小于阈值且前一数据大于阈值，判断两者之间的差值，若小于K，则转入下一数据；若大于K，则过程结束，将上一数据计入结束位置寄存器中。

数据筛选过程结束后，得到的离散数据进入寻峰算法阶段。

具体过程为：

1）在状态机转换处理后，得到了一组离散数据，将此数据进行高斯拟合，得到高斯函数的峰值点，记为A′。

2）非对称高斯拟合。由于受到多因素影响，采集的FBG信号波长在实际情况下为非对称，所以此处将非对称高斯模型（ft）引入，对高斯函数拟合得到的峰值进行校验补偿。公式如下：

非对称高斯模型（ft）为：

式中μ为高斯拟合函数所得峰值点所对应的时间点；σ1为高斯拟合函数左侧部分的时间点采样数；σ2为高斯拟合函数右侧部分的时间点采样数。

通过方差的判断并且由式1可推导出补偿后的峰值为：

式中A为校验补偿后的峰值。

2 实验结果与分析

本实验采用CCD分光仪检测法进行波长信号的解调，光谱解调仪波长检测范围为1 510～1 590 nm，解调分辨率为0.5 pm，精确度为1～3 pm，工作温度为0～50℃。在每个周期内，取其中的FBG3，FBG4反射谱分析，算法分别选取直接比较法，高斯拟合法，自适应半峰寻峰法，Steger寻峰算法以及本文提出的基于状态机的非对称高斯算法做对比实验，通过对比误差和速度，验证本文提出算法的有效性。

2.1 恒温寻峰误差比较

将恒温试验箱的温度设定为25℃，保证噪声等其他参数的稳定，光谱解调仪采集得到的光纤光栅理论中心波长值分别为：1 538.95 nm、1 545.02 nm。为了降低算法测量峰值的外在因素的影响，将所需算法分别采集10次进行平均，所求得的平均值与理论峰值进行比较，得出平均误差值，如表1所示。

表1 25℃下各寻峰算法的平均误差

通过表1，可分析得出，当外界环境稳定时，直接比较法误差较大，精度不高；高斯拟合法比直接比较法精度有所提高，但由于FBG反射光谱并非为对称光谱，所以与理论峰值比较起来，误差明显；自适应半峰检测寻峰法，虽然考虑到了非对称谱型的情况，通过补偿量进行峰值的修正，误差有所降低，但是由于补偿量为实验统计值，精度有待提高；基于Steger寻峰算法，结合超高斯模型，精度比自适应半峰寻峰算法高；本文所提出的算法，通过状态机的转换进行区域分割并考虑到峰值的偏移量问题，引入非对称高斯模型进行修正，误差降低，精确度得到提高。

2.2 变温寻峰误差比较

将传感器放入0～50℃的温控试验箱中，并且保证与上述恒温实验中有相同的参数，光谱解调仪分别5℃，10℃，15℃，20℃，25℃，30℃，35℃，40℃，45℃温度下采集10次数据取其平均值，并用上述算法同样在不同温度下采集10次得到平均峰值数据进行比较，如图3、图4所示。

图3 FBG3在变温下的各算法误差图

图4 FBG4在变温下的各算法误差

表2 变温下各寻峰算法的平均误差

通过图3，图4以及表2的分析可以得出，直接比较法无论从误差还是稳定性来说，效果都不是很理想；高斯拟合法由于未考虑不对称峰谱的情况，所以受到影响，稳定性和寻峰精度有待提升；自适应半峰检测法寻峰和基于Steger寻峰算法精度都优于高斯拟合法且受温度影响小；本文提出的算法，精度与其他算法相比，平均误差为0.40～0.55 pm之间，且稳定性好。

2.3 噪声寻峰误差比较

保持温度恒定在25℃，加入高斯白噪声，使得加入的噪音幅度占信号幅度的范围为0.001～0.1之间，测量10次取其平均值，计算误差，如图5、6所示。

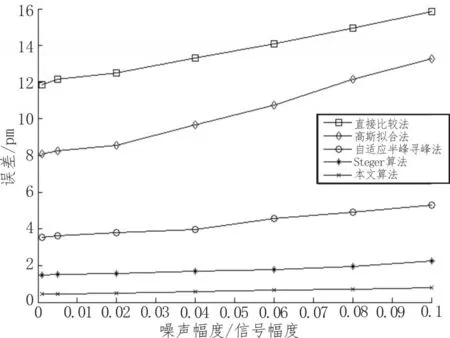
图5 FBG3在不同噪音下的各算法误差图

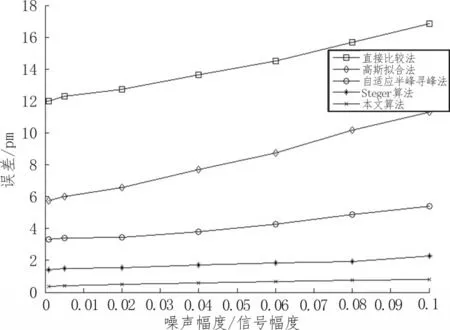
图6 FBG4在不同噪音下的各算法误差图

由图5、6分析可知，随着噪音幅度的加大，算法的精度都会受到影响。直接比较法影响最大，高斯拟合法次之，自适应半峰寻峰法平均误差在分别为4.21 pm、3.94 pm，基于Steger寻峰算法和本文所提出的算法受到影响产生的误差都在1.8 pm以下，抗干扰能力较强。

2.4 运行时间分析

通过上述实验，统计各算法的平均运行时间，可知直接比较法运行时间最短，为5 ms；自适应半峰检测寻峰算法次之，为55 ms；本文算法时间为90 ms；基于Steger寻峰算法为122 ms；高斯拟合法运行时间最长，为180 ms。以上算法在时间上都可以满足实际应用中波长解调的实时性要求。

3 结束语

文中首先在巴特沃斯低通滤波预处理的基础上，通过状态机之间的相互转换完成对数据的进一步处理，引入非对称高斯模型，对峰值进行补偿修正。通过实验，分析比较了在恒温环境下以及不同温度和噪音的干扰下对寻峰算法的影响。实验结果表明，本文所提算法相较于直接比较寻峰法和高斯拟合算法在精度和稳定性上都有显著优势，而对于同样考虑到非对称问题的自适应半峰检测寻峰法和Steger算法，则在精度和时间上优于此两种算法。综上所述，本算法在FPGA超强的可编程并行计算对波长信号进行滤波寻峰处理的基础上，既弥补了传统算法对于非对称忽略的问题，又避免了存储空间的浪费，同时在速度和精度上，都得到了提升。

[1]Wada A，Tanaka S，Takahashi N.Optical fiber vibration sensor using FBG Fabry- Perot interferometer with wavelength scanning and Fourier analysis[J].IEEE Sensor Journal，2012，12（1）:225-229.

[2]Bodendorfer T，Muller M S，Hirth F，et al.Comparison ofdifferentpeak algorithmswith regards to spectrumetric fiber Bragg grating interrogation systems[C]//International Symposium on Optomechatronic Technologies，2009：122-126.

[3]蔡能宏，闫连山，陈娟子，等.基于可调谐F-P滤波器的光纤光栅传感解调系统寻峰算法对比分析[J].仪表技术与传感器，2013，33（4）:100-106.

[4]薛双喜，马艳，王向辉，等.多通道光纤布喇格光栅传感器同步解调系统[J].电子设计工程，2012，20（7）:173-175.

[5]陈志军，白剑，吴祖堂，等.光纤布喇格光栅反射谱寻峰算法优化及比较[J].光子学报，2015，44（11）:83-88.

[6]Frederic C J，Cicero F M.Peak detection algorithm for fiber Bragg grating sensors[C]//Latin America Optics and Photonics Conference，2012:LM2A.8.

[7]王拥军，刘永超，张靖涛，等.高速高分辨率光纤布拉格光栅传感系统的解调技术[J].中国激光，2013，40（2）:151-156.

[8]沈漫，董雷，于本化，等.一种用于光纤布拉格光栅传感的自适应寻峰算法[J]，电子测试，2014，9（6）:27-28.

[9]朱梅，张淼，胡立章，等.光纤布喇格光栅中心波长检测中的寻峰算法[J].光通信研究，2011，167（5）:60-63．

[10]胡辽林，王亚萍，王斌.光纤光栅传感信号寻峰误差研究[J].西安理工大学学报，2015，31（4）:409-413.

[11]余有龙，王雪微，王浩.不同采样方式下光纤布喇格光栅反射谱寻峰算法的分析[J].光子学报，2012，41（11）:1274-1278.

[12]王巧妮，杨远洪.基于Steger图像算法的光纤布拉格光栅寻峰技术[J].光学学报，2014，34（8）:133-138.

[13]刘泉，蔡林均，李政颖等.高速度高精度光纤布拉格光栅解调的寻峰算法研究[J].光电子·激光，2012，23（7）:1233-1239.

[14]郑希科，李根，李静，等.基于非对称广义高斯模型的渡越时间确定方法[J].大庆石油地质与开发，2015，34（4）:143-147.