众筹平台的双层网络信息传播模型研究

周冬梅，陈 婷，赵闻文

(1. 电子科技大学经济与管理学院 成都 611731; 2. 电子科技大学计算机科学与工程学院 成都 611731)

众筹是植根于众包的更广泛的概念，它是通过人群获得想法、反馈和解决方案的企业活动[1-3]。众筹平台上的网络关系跨越了现实世界(线下网络)和虚拟世界(线上网络)，其中线下网络关系主要指众筹参与者在开始众筹活动前所拥有的网络关系；线上网络关系则包含了两个部分：线下所继承的网络关系和通过众筹平台所拓展的网络关系。众筹平台上的网络关系是真实世界社会关系中的联系、结构、信任、规范等宏观和微观规则在虚拟世界的呈现，故本研究基于社会资本理论中的网络关系、信任及信息价值等概念，阐述了众筹平台的双层网络信息传递过程。在众筹平台上，同层网络之间的结点转变，其本质是传播对象进行信息扩散、演化和更新的过程，这一机理过程也同样适用于两层耦合网络。

多层耦合网络模型是最新的复杂网络研究范式，其定义为：网络中的各层共同使用同一结点集合，但各层之间的结点属性和边属性都截然不同，同时层与层的结点之间存在耦合作用。一般有相互依赖、协作和竞争3种关系，不同的关系呈现多层网络不同的拓扑结构。本文将这3种关系分别表述为度度正相关、度度负相关以及无相关，体现在网络拓扑结构上则为3种不同的层间连接模式(同配、异配以及随机连接)。学者们根据信息传播的特点[4-7]，不断改进网络模型，本文借鉴文献[8]提出的匹配系数的概念将正负相关性问题进行了量化，并据此建立了众筹平台的单层和双层信息传播模型，对不同条件下的传播进行了仿真试验。

1 众筹平台的双层网络信息传播机制

虽然分析视角略有差异，但归纳可以发现：众筹平台的多层网络主要由线下网络和线上网络两部分构成。线上网络代表一个在线交流平台，在文中指众筹平台，每个结点表示的是线上进行社交的用户或某个帐号，结点中间的连边代表的是用户间的关注或在线用户间的好友关系。现实世界中，物理接触的个体用线下网络来表示，其中每个个体用结点来表示，而这些结点之间的连边代表社会网络中个体与个体之间的面对面交流。

在众筹平台上信息传递过程为：1)线下网络的信息传递。在众筹项目初始阶段，密切的朋友成为主要的支持者，而这些支持者认为他们是有义务将信息传播给自己认识的人。2)线上网络的信息传递。当个体看到许多人购买某产品时，他们推断这个产品是好的、应该被购买，这种行为在线上也是发生的[9-11]。3)跨越线上和线下网络的信息传递。线上网络的消费体验促进了支持者在线下的信息传递，支持者认为有必要把消费体验与他人分享，例如在Twitter、Facebook、微信和微博中，人们可以很容易的将信息传递给他们的朋友。

无论是线下网络还是线上网络，支持者之间的连接关系以及支持者的信任度是一个动态演变的过程。而复杂网络中每个时间步t呈现不同的拓扑结构，当某结点因一次疏忽传播了一条“坏”消息时，其在整个网络中的信任度将大大折扣。因此，本文基于KSCC(K-shelland community centrality in coupled networks)系统指标提出了双层耦合网络中结点信任度的测量方式，并将其用于信息传播驱动的线上-线下耦合演化模型，用来衡量信息的传播范围。

2 单层众筹平台信息传播模型

借鉴多层耦合网络理论以及传播动力学理论，本文在SCIR模型的基础上[12]，依据众筹平台信息传播机制，建立了单层众筹平台信息传播模型(S-SCIR model)，并根据多层耦合网络的信息传播模型将众筹平台中的结点状态分为4类：未知态S，已知态C，传播态I以及免疫态R。

S态代表某个体没有接受过来自邻居的信息；

C态代表某个体接受过来自邻居结点的信息，但并不十分信任该信息，故不一定会转发信息；

I态代表某个体接受并传播了邻居结点传来的信息；

R态代表某个体知道某信息，但对该信息并不感兴趣，故不会转发该信息。

基于现实情况，本文认为每个个体拥有不同的传播概率。假设传播信息结点i处于S态，然后以概率φ接受其他信息变为C态，否则继续保持S态；C态结点以概率δ将信息传播在众筹平台中，并转变成为I态，否则以概率θ阅读该信息但不进行转发并转变成R态；I态结点对信息失去兴趣或者对信息并不信任，将以概率β转化为R态，考虑到一个用户不可能对一条信息永远饱含兴趣，终将转变为R态，因此本文设定β=1。根据以上所述，本文用不同类型结点的状态转移图来表示单层众筹平台的信息传播模型，如图1所示。

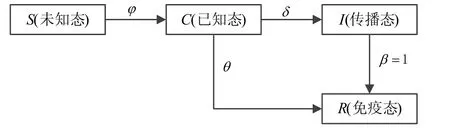
图1 单层众筹平台的信息传播过程图

2.1 模型相关定义

定义 1连边权重：本模型中有向连边的权重为节点间的交互频率，即近段时间节点间的单向转发次数。在双层耦合网络中，表示为内网权重ωij-in和外网权重ωij-out，分别表示结点与本层、外层网络邻居结点之间的连边权重。

定义 2结点的度：也称连通度，指与该结点连接的边数，表示结点在网络中的影响力和重要程度。双层耦合网络中结点i的度分为Ki-in和Ki-out，分别表示结点i与本层网络、外网有交互作用的结点数目。

定义 3信息价值：信息价值包含信息热点度、信息内容与用户的吻合度以及传播用户影响力3个方面。信息对于用户的重要程度V0，0代表信息毫无价值，1代表信息具有巨大价值。

定义 4信息时效性特征标度因子λ：由于网络信息的海量复杂性，用户对信息的关注有一定的时效，参数λ体现信息在网络中的“三分钟热度”特性以及信息价值的时效性。

2.2 单层网络结点信任度

众所周知，用户往往是从直接邻居中选择性的接收消息，因此当直接邻居在传播信息时，其影响力的大小将作为该结点是否接收该信息的判断条件之一。本文通过连边权重度量结点信任度ω，表示为该结点与K个邻居结点之间连边权重的加权平均：

2.3 信息价值

本文将信息价值与用户影响力相关联，并考虑到信息具有时效性，引入信息时效性特征标度因子λ。

定义 5信息吸引力函数φ(t)表示结点接受信息的偏好程度，即结点从S态转变为C态的概率：

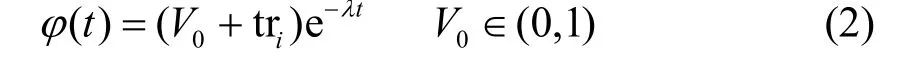
在单层的众筹平台中，假设存在N个网络结点，由于在较短时间内，新增加的和减少的结点数可以大致相互平衡，故本文认为所有状态的结点总数在任何时刻都保持N不变。用S(t)、C(t)、I(t)和R(t)分别表示在t时刻处于未知状态、已知状态、传播状态和免疫状态的结点数。在S-SCIR模型中，假设t时刻处于S态的结点数S(t)是连续可导的，且每分钟将有φS(t)个结点接受到来自邻居结点的信息，然后转变为C态，其余结点将保持S态不变。因此，在t+Δt时刻有：

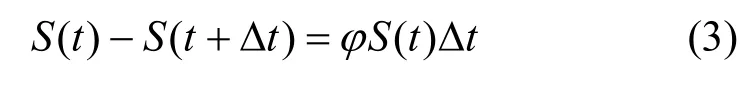
由上式可得：

相似地，可得C(t),I(t),R(t)的微分方程：

以上4个式子依次表示结点处于S态、C态、I态和R态随时间的变化率。

3 双层众筹平台信息传播模型

众筹平台是由线上网络和线下网络交叉组合形成的，在S-SCIR模型的基础上，建立了双层众筹平台模型(coupling susceptible contacted infected1 infecte2 recovered, O-SCI2R)。

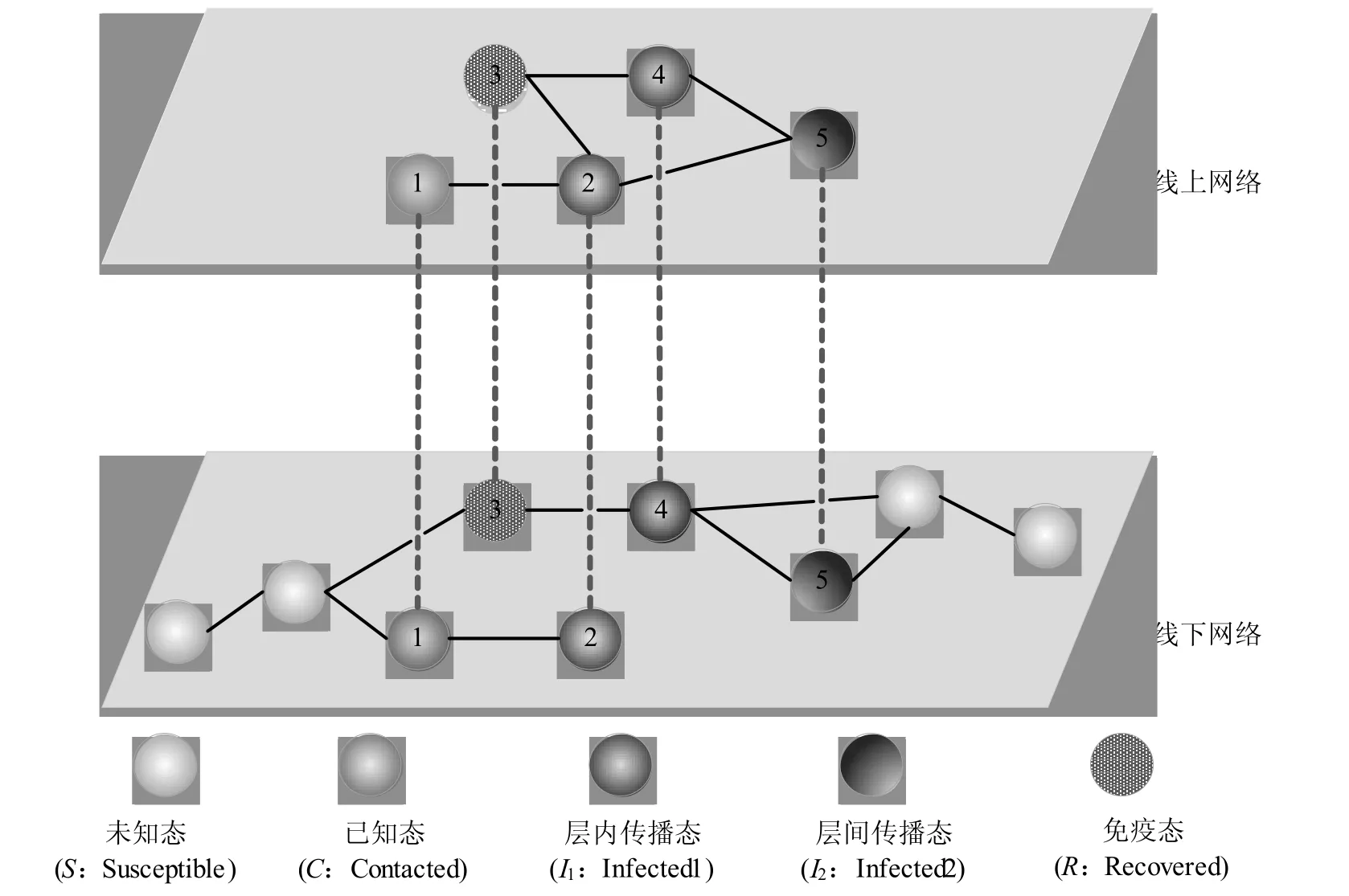
图2 线上线下网络模型示意图

在如图2所示的双层耦合网络中，用网络A和网络B分别表示线上网络和线下网络，其中线上网络A中的每一个结点都与线下网络B中的结点一一对应，表示它们属于同一个体，分别处于不同的网络层中，反之亦然(本文暂不考虑多个线上账户由同一现实个体注册使用的情况，即网络A中的多个结点对应于网络B中的某一个结点的情况)。网络信息和物理信息分别在网络A和B中进行传递，结点表示众筹平台中参与者及其可以辐射的社会网络范围中的个体，结点之间的连边表示个体之间的好友关系，信息会沿着边进行传播。

借助传染病传播动力学的研究结果，并结合S-SCIR模型中信息传播的过程，将众筹平台中支持者的主体状态分为已知态(C态)、免疫态(R态)、未知态(S态)、层内传播态(I1态)和层间传播态(I2态)。其中，层内传播态和层间传播态的主体都阅读了来自邻居结点的信息，但层内传播态是将信息转发到同层网络，而层间传播态则是将信息转发到其他网络。

3.1 双层耦合网络层间连接模式

根据耦合网络间关联结点的度度相关性，本文在构建众筹平台下信息传播的耦合网络结构模型时，主要采用度度正相关、度度负相关以及随机连接3种不同的耦合连接模式，为简化双层耦合网络模型分析的实现过程，规定：

1)假设线上网络和线下网络具有同样的规模和尺寸，且不同网络之间的结点是一对一的对应连接关系。在考虑结点数量相同的双层耦合网络基础上，可以将其方法扩展到任意规模的耦合网络。

2)在构建时，首先在各自的网络中对全部耦合结点按度的大小进行排序，然后根据层间同配连接、层间异配连接和层间随机连接3种不同的连接模式创建不同的耦合网络。

黄炎培的这一招很起作用。他的申述得到大多数参政员的同情和支持。他回家之后，傅斯年就去找邵力子、雷震两位秘书长，说：“戴笠是奉何人之命去包围、搜查黄参政员的家的？他这样任意妄为怎么行？他今天可以搜查黄参政员的家，明天岂不又去搜查其他参政员的家？戴笠这样搞，我们参政会这块牌子的面子还要不要保住？参政员的尊严还要不要维护？请你们二位将这件事面报国民政府蒋主席，要求他下令惩治戴笠，以平息正在开会的国民参政会同仁的愤怒之情。”还有一些参政员用拒绝出席会议的形式抗议戴笠搜查黄炎培住宅的非法行为。

对于层间同配连接(assorative link, AL)，其线上网络A中用户和线下网络B中的个体按照结点度的大小连接，即线上网络A中度大的用户连接线下网络B中度大的个体，线上网络A中度小的用户连接线下网络B中度小的个体，又称正相关连接。当结点度相同时，则进行随机排序选择。按照Ai↔Bj依次建立双层耦合网络之间结点一对一的连接模式。

而层间异配连接(disassortative link, DL)则与层间同配连接相反，其线上网络A中度大的用户连接线下网络B中度小的个体，线上网络A中度小的用户连接线下网络B中度大的个体，故又称负相关连接。按照Ai↔Bj(j=N-i+1)建立耦合网络之间一对一的连接模式。

层间随机连接random link (RL)：线上网络A中的结点随机连接线下网络B中的结点，并构成线上线下网络结点一对一的连接模式。

3.2 双层耦合网络层间信息传播模型

和单层网络一样，考虑到一条连接只使用一次，传播模型中的个体存在社会加强作用和记忆效应的特点，本文认为个体状态的转换概率是不同的。这里假设信息在线上网络A进行发布，网络A中S态结点以概率φ向C态结点转化；C态结点以概率δ1将信息转发到本层网络中，变成I1态，或以概率δ2将信息转发到线下网络B中，成为I2态结点，此处的概率δ2作为信息的上传/下载率；或者以概率θ阅读信息但不转发，成为R态结点；I1和I2结点分别以概率β1和β2转变成R态。双层众筹平台状态转移图如图3所示，图3a展示了双层耦合网络中层内信息传播过程，图3b展示了结点在双层网络间的信息传播过程。

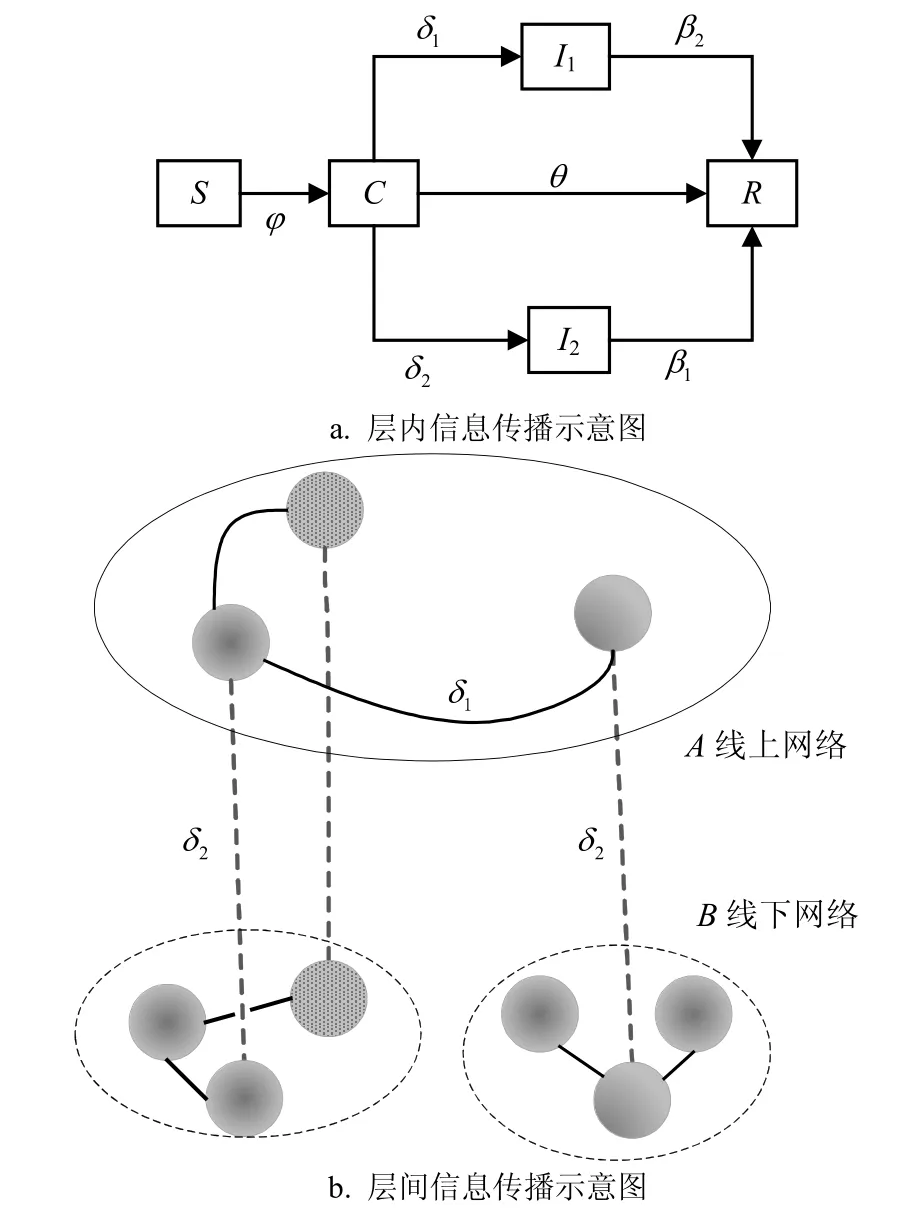
图3 双层耦合网络信息传播过程示意图

t时刻，线下线下网络中不同状态主体的数目分别表示为：未知者S(t)、已知者C(t)、层内传播者I1(t)、层间传播者I2(t)、免疫者R(t)。则总的主体数为N=S(t)+C(t)+I1(t)+I2(t)+R(t)。利用系统动力学建模思想，通过微分方程组建立双层众筹平台模型，该模型对应的微分方程为：

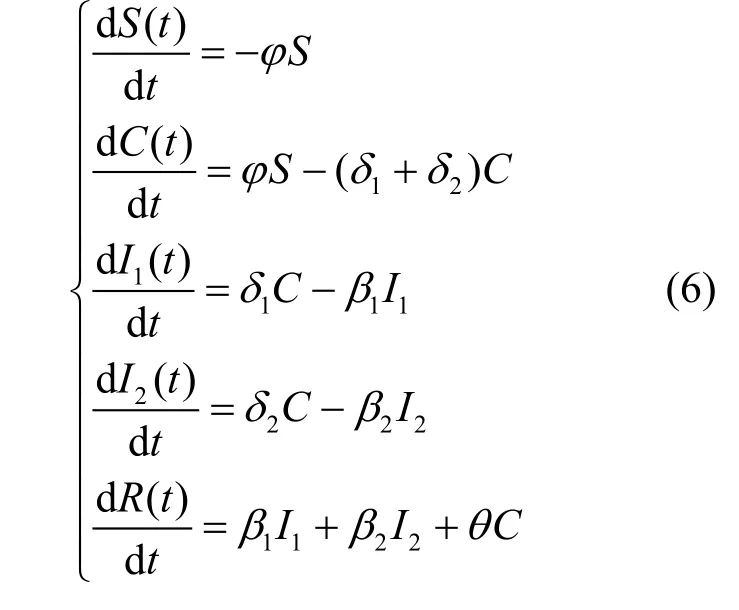
式中，5个式子依次表示结点处于S态、C态、I1态、I2态和R态随时间的变化率。

3.3 匹配系数

针对复杂网络中结点间的度相关特征，Newman提出匹配系数的概念来对其量化：

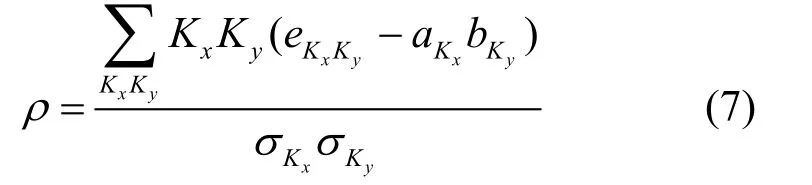
式中，eKxKy表示网络所有边中连接度为Kx和Ky的边所占的比例；aKx,bKy表示度为Kx,Ky的边所占的比例；是随机变量Kx的方差。

其中，-1≤ρ≤1，ρ＞0表示同配连接，即大度值结点倾向于和大度值结点连接，越大，正相关性越强；ρ＜0表示异配，即大度值结点倾向于和小度值结点相连，越大，负相关性越强。通过计算多个真实世界网络匹配系数极值ρmax和ρmin，发现一般网络的匹配系数满足-1＜ρmin＜ρmax＜1，当ρ=1时为完全同配连接；ρ=-1时为完全异配连接；ρ=0时表示网络结构具有随机不相关特性。

3.4 双层网络结点信任度

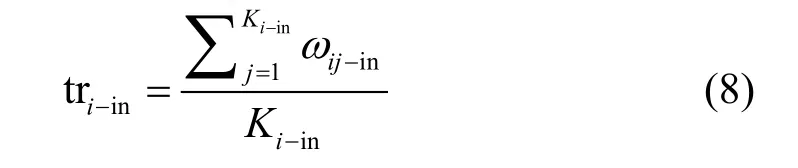
结点i的外信任度表示结点i在其他层网络中的信任度，通过Ki-out和ωij-out表示为：

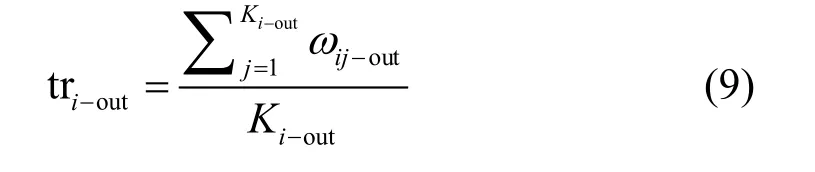
综合结点的内外信任度，本文结合指标KSCC以及双层耦合网络下结点的内外信任度来衡量双层耦合网络的结点信任：

和单层网络一样，双层耦合网络传播的信息同样存在用户接受信息的不同偏好现象。不同价值的信息，其用户吸引力也不同，结合KSCC值表征节点在网络中的影响力，则S态结点转变为C态结点的转移概率：

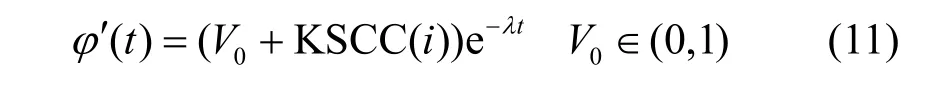
4 建模与仿真

为探索信息在不同网络条件下的传播情况，本文使用Matable工具对S-SCIR模型和O-SCI2R模型进行仿真实验，通过改变参数取值分析信息的传播规律。

本文对结点平均度均为5的单层网络在S-SCIR模型上进行数值仿真。对模型中的各项参数进行设定：假设用户数量(结点总数量)N=10 000，在t=0时，S(0)=9 999，C(0)=0，I(0)=1，R(0)=0。随机选择一个结点作为传播源，假定δ=0.85，θ=0.15，β=1，特征标度因子λ=4，信息价值V0=0.2。

为方便对比，同样对结点平均度为5的线上网络A和线下网络B在O-SCI2R模型上进行数值仿真。线上线下网络结点数量NA=NB=10 000，在t=0时，S(0)=9 999,C(0)=0,I1(0)=1,I2(0)=1,R(0)=0。随机选择一个结点作为信息的传播源，特征标度因子λ=4，信息价值V0=0.2，内部影响因子α=0.5，外部影响因子β=0.5，各传播率δ1=0.85,δ2=0.15，θ=0.05，β1=1，β2=1。

因结点状态由I态转化为R态的概率均为1，便可用最终态R态结点的数量替代I态结点的累积量，故模型中用表示信息传播过程中传播信息结点的累积数量比例，R值越大，表示信息的覆盖率越大。

1)单层网络和双层耦合网络对信息传播的影响

从仿真结果可以发现：① 在参数均相同的条件下，双层网络的R态结点明显多于单层网络，验证了双层网络会扩大信息传播的规模。② 对这两种网络结构的信息传播范围，双层网络和单层网络相比较，并不是简单的两倍组合。例如，在t＞14时，单层网络大致保持0.1不变，而双层网络则保持在0.3左右，是单层网络的两倍多，说明双层网络相比于单层网络并不是简单的将信息传播规模扩大为两倍。③ 由曲线走势可以看出，不管信息在单层网络还是双层网络下传播，值最终都将趋于稳定状态。而双层网络在大约t=8时，R态结点数量会达到一个峰值，在t＞8时，双层网络中R态结点基本保持不变；而单层网络在大约t=12时，R态结点会达到一个峰值，在t＞12时，单层网络中R态结点数目也基本保持不变，说明信息在双层网络下传播速度明显大于单层网络，并且信息在网络中的传播终将停止，不会永无止境的传播下去。

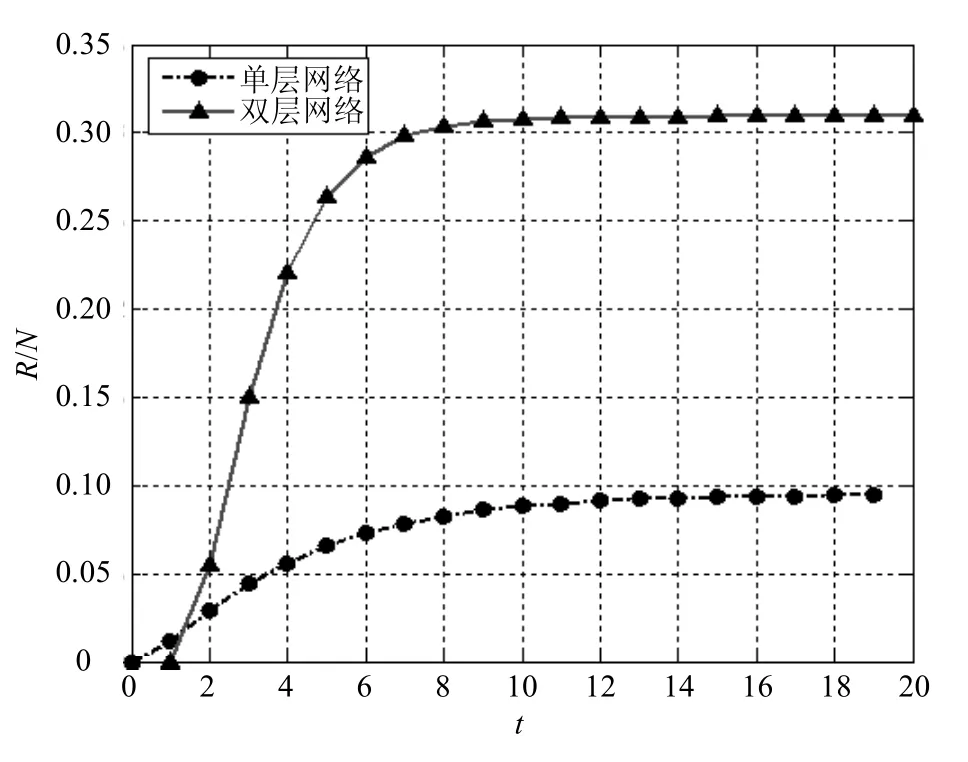
图4 单层网络与双层耦合网络比较

2)层间耦合连接模式对信息传播的影响

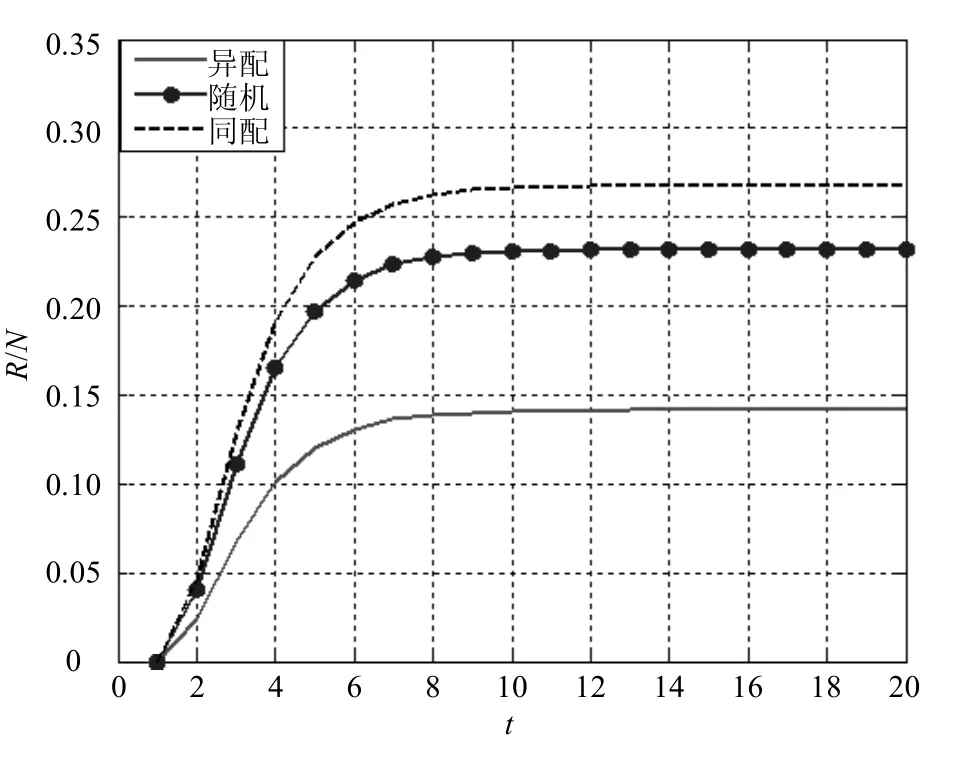
图5 同配、随机和异配连接模式比较

可以发现：在参数均相同的条件下，同配连接模式下的信息传播范围最广，说明接收到信息的个体最多；而异配连接模式下的信息覆盖范围最小，接收到信息的个体累积数量最小。说明3种层间连接模式中，同配连接最有利于信息传播，而异配连接最不利于信息传播。

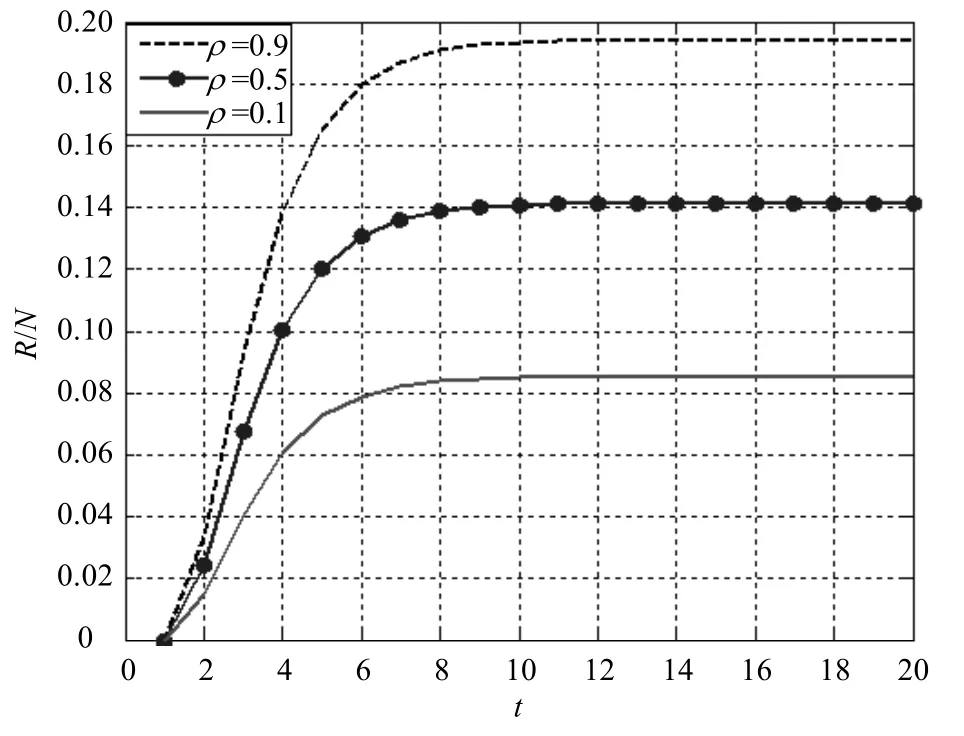
图6 度度正相关连接模式比较

可以发现：随着ρ的增大，即线上网络中的结点与线下网络中的结点正相关性增强，值也在逐渐增大。表明网络中的消息传播者越多，使得消息的覆盖率越广，越有利于促进消息的传播。

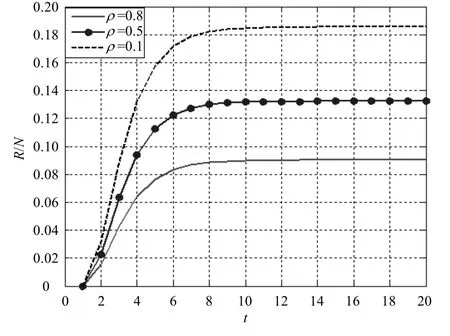
图7 度度负相关连接模式比较

由图可以发现：随着ρ的不断增大，即线上网络中的结点与线下网络中的结点负相关性增强，值却逐渐减小，表明线上网络中的结点与线下网中的结点负相关性越强，消息的传播者越少，使得消息的覆盖率越小，越不利于网络中消息的传播。

3)信息价值对双层网络中信息传播的影响

以同配连接模式为例，设置信息价值参数V0为0.1，0.5，0.9，为消除其他影响，其余参数保持初始的设定值。不同信息价值随t的演化情况如图8所示。

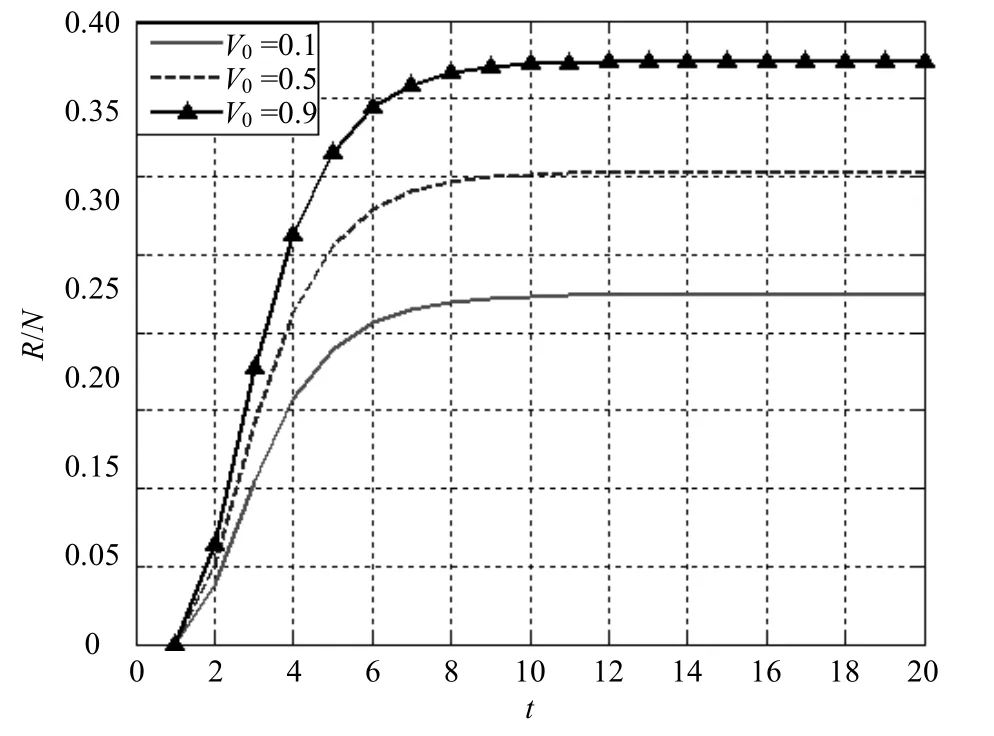
图8 信息价值对信息传播的影响

根据信息价值的定义，信息价值参数V0越大，该信息的价值越大。从图中可以发现：随着V0的增大，也在不断增大，表明价值越大的信息在网络中传播范围越广。所以，信息的传播范围在一定程度上也与信息价值有关，内容越吸引用户，并且传播载体的影响力越大，可以使该信息的传播范围在同样的传播模型下覆盖网络的面积越大。

5 结 束 语

本文借鉴多层耦合网络理论以及传播动力学理论和方法，在SCIR模型基础上，根据众筹平台信息传播的机制，建立了单层众筹平台信息传播模型S-SCIR和双层众筹平台模型O-SCI2R，探索了信息在不同网络条件下的传递情况。研究结果显示，借助互联网的发展，众筹平台这个线上线下双层耦合网络比传统的单层网络更有利于信息的传播，同时其连接模式和信息价值也对信息传播产生影响。可以发现，众筹信息在线下网络的传播可能引发其在线上网络中的扩散，并最终可能导致一个信息级联效应。因而，对于众筹平台的项目发起者而言，其本身所拥有的线下网络、发起的项目内容以及后期的包装在一定程度上将影响最终获得的筹款。

本研究通过模拟信息在众筹过程中线上线下网络的传递过程，挖掘了影响众筹信息传播的因素，为本类问题的研究提供了一种新的视角和方法。这种方法简单客观，可以获得真实的量化数据。但本研究中的相关数据只是简单模拟的结果，与真实的网络传递存在一定差异，这也为后续的研究提出了新的要求。

[1]GAGLOEVA A, ASANKOZHOEVA R. Marketing in crowdfunding： an exploratory study of crowdfundingin the context of entrepreneurialmarketing[D]. Sweden： Lund University, 2014.

[2]BELLEFLAMME P, LAMBERT T, SCHWIENBACHE A,et al. Crowdfunding： Tapping the right crowd[J]. Journal of Business Venturing, 2014, 29(5)： 585.

[3]CHOLAKOVA M, CLARYSSE B. Does the possibility to make equity investments in crowdfunding projects crowd out reward-based investments?[J]. Entrepreneurship Theory and Practice, 2015, 39(1)： 145-172.

[4]王建伟, 荣莉莉, 王铎. 基于结点局域特征的复杂网络上相继故障模型[J]. 管理科学学报, 2010, 13(8)： 42-50.WANG Jian-wei, RONG Li-li, WANG Duo. Model forcascading failures on complex networks based on local characteristics of nodes[J]. Journal of Management Sciences in China, 2010, 13(8)： 42-50.

[5]李稳国,邓曙光,杨冰, 等. 相互依存网络间的拓扑构建方法[J]. 计算机工程与应用, 2014, 50(11)： 85-89.LI Wen-guo, DENG Shu-guang, YANG Bing, et al.Topological coupling method between interdependent networks[J]. Computer Engineering and Applications, 2014,50(11)： 85-89.

[6]WANG J W, JIANG C, QIAN J F. Robustness of interdependent networks with different link patterns against cascading failures[J]. Physica A, 2014, 393： 535-541.

[7]YAGANO, QIAN D, ZHANG J, et al. Conjoining speeds up information diffusion in overlaying social-physical networks[J]. IEEE Journal on Selected Areas in Communications, 2013, 31(6)： 1038-1048.

[8]NEWMAN M E. Spread of epidemic disease on networks[J].Physical Review E, 2002, 66(1)： 016128.

[9]FISCHER E, REUBER A R. Online entrepreneurial communication： Mitigating uncertainty and increasing differentiation via Twitter[J]. Journal of Business Venturing,2014, 29(4)：565-583.

[10]TAN J, ZHANG H, WANG L. Network closure or structural hole? The conditioning effects of network-level social capital on innovation performance[J].Entrepreneurship Theory & Practice, 2014, 39(5)：1189-1212.

[11]PATEL P, TERJESEN S. Complementary effects of network range and tie strength in enhancing transnational venture performance[J]. Strategic Entrepreneurship Journal,2011, 5(1)： 58- 80.

[12]于凯. 双层耦合网络上的信息传播模型研究[D]. 大连：大连理工大学, 2015.YU Kai. Research on information spreading model on bilayer coupled networks[D]. Dalian： Dalian University of Technology, 2015.