天线孔径动态分割下的雷达一体化系统资源调度

娄 昊，张 群，罗 迎，陈怡君，何其芳

(1. 空军工程大学信息与导航学院 西安 710077；2. 武警工程大学信息工程系 西安 710086)

当前，把雷达、通信、电子战等不同种类、不同用途的设备进行整合，构成一体化的电子系统已经成为一种新的研究方向[1-2]。其中，天线孔径的共享是研究重点之一。文献[3-4]指出，共享天线孔径的方法主要有两种。一种是多种功能使用一个通用孔径，时间互相交错，如美国雷声公司在AN/APG77型机载雷达上加装了通信调制解调器后即可实现高速数据传输[5]；另一种是将一个大的孔径分割成多个子孔径，可同时实现雷达、通信和电子战等功能，如美国海军实验室于1996年启动的先进多功能射频概念(AMRFC)计划就是基于天线阵列孔径分割、收发分离来实现多种功能一体化[6]。

考虑到这种体制下天线阵元的功能可以随时间进行切换，则天线阵面可以实现动态分割，使得天线在执行多项任务的同时进行功能的动态切换。此时，在雷达-通信共享系统面对多种任务时，如何在有限时间内完成更多的任务成为重要的研究课题。尤其在第二种基于动态孔径分割的天线共享方式下，当任务较多时，需要在时间和孔径两个维度进行任务管理和调度，从而优化系统的整体效能。

从目前的研究来看，常用的多功能雷达资源调度方法大致可分为模板法[7]、自适应调度方法[8]、动态优先级EDF(earliest deadline first)[9-10]等。其中，EDF方法在正常任务负载下表现出很高的性能，受到了较多的关注，当任务较重时，仍然具有较高的任务丢失率[11]。不过，现有文献针对天线孔径动态分割条件下的任务调度问题研究较少，仅在文献[12]等少数文献中提及。本文在天线孔径动态分割和多功能雷达任务调度技术的基础上，提出了雷达通信一体化下的时间、孔径二维资源管理问题，并根据先入先出(first in first out, FIFO)原则提出适合该问题的任务调度算法。

1 问题建模

AMRFC方案将多功能共享的相控阵天线划分为多个独立子孔径，每个子孔径能够单独工作在不同状态[1]。孔径的组合方式非常灵活，比如按照1个子孔径、两个子孔径和1个象限合成一个天线阵列，甚至可以将整个孔径合成同一个天线阵列。假设每个子孔径能根据需求执行不同的任务类型，包括搜索、跟踪、成像和通信等，而每个任务类型需要的子孔径数量不同。文献[12]提出的天线孔径共享方法按照孔径面积百分比的方法动态分配天线资源，即每个子孔径无论是否相邻都可以直接组合起来执行任务，类似于计算机分布处理条件下的进程管理问题[13]。然而，考虑到天线间距的影响，相距不同的阵元、子孔径不分区别的组合执行同一功能，很可能对系统增益、天线方向图等参数性能产生较大的影响。以线阵天线为例，假设阵列由K个天线阵元组成，阵元间距为d，第m个阵元的激励幅度为{am}，并设天线阵元间距相同，都为半波长λ/2，波达方向为阵列法向，则阵列的辐射方向图可表示为：

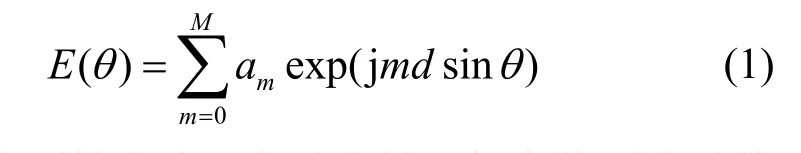
若将阵列等分为M个子孔径，每个阵列阵元数量为K/M，并组成线性组合S={s0,s1,…,sM-1}，若1个或多个相邻的子孔径合成若干天线方向图，如图1a所示，此时M=4，4个子孔径分别形成的两个天线阵列方向图E0(θ)和E1(θ)可以表示为：

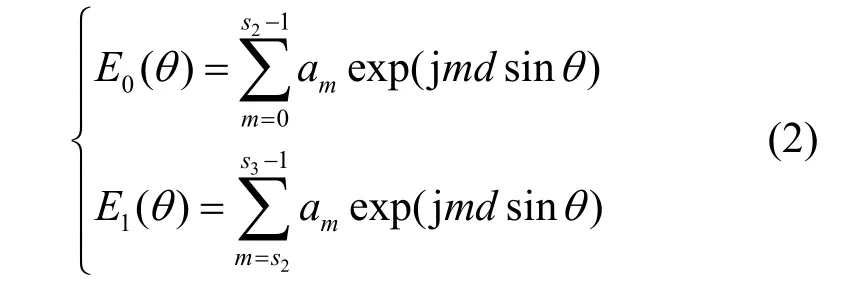
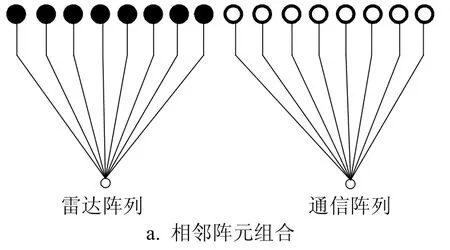
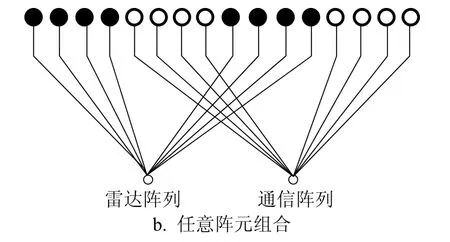
图1 天线阵列孔径动态分割示意图

一旦整个阵列对各个功能进行交错设计，即每个子阵列任意合成天线，如图1b所示，则此时形成的两个天线方向图E0′(θ)和E1′(θ)可表示为：

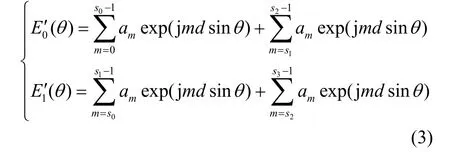
上式与式(2)存在差别，按照式(3)得到的各个天线的方向图不一定满足辐射要求。因此，本文假设只有相邻的天线子孔径能够直接组合起来执行同一任务；且随着时间t的变化，相邻的子孔径可以重新组合，从而执行新的任务。

2 调度算法设计

如果将多功能天线的孔径和时间都视为资源的话，则在这两个维度上都存在资源管理和分配问题。二维资源调度的一个典型应用是矩形件排样问题[14]，该问题可描述为：给定一组矩形件的尺寸，在一个宽度、高度有限的矩形板材上不重叠地、尽量多地排入这些矩形件，使得板材利用率达到最高。在求解该问题时一种经典的方法是最低水平线方法[15]。“最低水平线”是指在矩形板材上水平方向上最低处的高度线，以此为下一个矩形件的排样位置。与之类似，天线孔径动态分割下的雷达一体化系统中任务到达是按照时间先后进行的，可以定义一个以时间为中心的任务预执行矩阵作为任务排入的依据，且随着任务的更新而更新。需要注意的是，天线任务一般都有时间要求，即有“生存期”，若到达一定的截止时间，任务仍未执行，则该任务就“死亡”，不能再加入队列。

对于这类问题，最直接、最简单的处理方法是将到达的任务随机安置到天线孔径中，如果当前位置恰好没有任务，则顺利执行；如果当前孔径有任务正在执行，则将该任务推迟执行。本文将这种方法视为“随机孔径”策略。

2.1 数据定义

为便于计算机自动处理，在进行算法设计前先进行如下定义，也即算法的数据结构：

1)资源矩阵RNT×M。将时间t离散化为NT个“时间片”，天线孔径由M个子孔径组成，并生成二维时间-孔径资源矩阵RNT×M，其中rNi,m={0,1}∈RNT×M表示矩阵元素被占用情况。

2)任务向量Ak={Nak,Wk,ωk,Lk}，Nak表示任务到来的时刻，Wk表示执行时间长度，ωk为任务生存期，Lk为占用孔径资源的大小；其中ωk表示任务Ak的最晚执行延迟时间，即到Nak+ωk时刻任务Ak还没有执行则该任务失效。

3)任务预执行矩阵Bk，表示当前任务可供利用的时间、孔径资源矩阵，由M1(M1＜M)个矢量Bk={Npk,sk,ηk}组成，其中Npk表示可供执行任务的时刻，sk表示可供执行的孔径起始位置，ηk为剩余的孔径资源。

4)任务执行向量Eq，描述了任务的实际执行时间、孔径位置特性，Eq={Neq,sq,nq}，其中Neq表示任务的实际执行时间，sq表示任务实际执行的孔径位置，nq表示Eq的任务序号。

2.2 更新规则

2.1 节中定义的预执行矩阵Bk包括时间、孔径位置等内容，实际上是描述了现有的空闲时间-孔径资源，其数值应当伴随着任务的增加不断更新。更新过程可简化为“增”“改”“删”“重排”4个步骤，现整理如下：

1)元素增加。沿着时间增加的方向N→NT，根据对应的孔径占用情况，找到第一个未占用的子孔径，记录此时的时间N0和可用孔径的起始位置s0，沿着孔径方向向下找到被占用的孔径位置计算可用的孔径大小η0=s0′-s0，则记录Bk中第一个元素b0={N0,s0,η0}；

2)元素修改。随着时间N的增长，按照步骤1)增加新元素bi={Ni,si,ηi}，如图2中的b1～b4，其中，某一时间Ni可能出现多个可用子孔径，即同一时刻、子孔径初始位置不同，如此时bi={Ni,si,ηi}，bi+1={Ni+1=Ni,si+1,ηi+1}(其中si+1＞si)；

3)元素删除。时间非连续占用引起的预执行矩阵“遮挡效应”，使得Bk中部分元素失效，需要在更新时删除。如图2所示，新任务的到来与现有预执行矩阵Bk中存在时间空隙，按照步骤1)，Bk中新增2个元素b5={N5,s5,η5}和b6={N6,s6,η6}，然而b5对b2、b4造成了遮挡，b2、b4表示的位置无法放入新到任务；预执行矩阵Bk中删除b2、b4，即此时Bk只包括b1、b3、b5、b6。判断是否存在遮挡的规则是：对于新元素bi={Ni,si,ηi}，当si≠0时，需要判断∀j＜i，是否存在bj={Nj,sj,ηj}且Nj≤Ni,sj≤si；如果存在，则对应bj删除，且整个矩阵Bk重新排列。

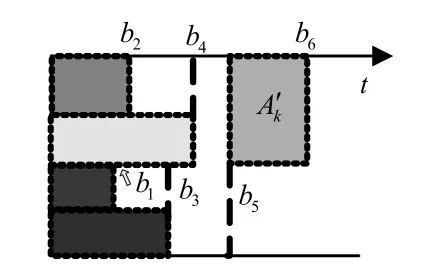
图2 预执行矩阵Bk元素删除示意图

4)元素重排。矩阵Bk的最后一个元素修正为

2.3 调度算法

在以上内容基础上，本文算法表述如下：

1)初始化资源。将时间划分为NT个时间片，孔径大小为M，建立二维时间-孔径的资源矩阵RNT×M，初始化资源矩阵RNT×M=0NT×M。

2)初始化任务。将时间节点k需要执行的任务生成任务请求向量Ak，令k=0，q=0。

3)按照第2.2节方法生成预执行矩阵Bk。

4)在预执行矩阵Bk基础上，判断当前任务Ak是否可执行，并在执行后更新Bk：

① 若Nak≥NM-1，即Ak在Bk的时间右侧(较Bk晚)，也即将Ak与Bk比较，仅小于最后一个元素BM1，即Nak＞Ni(0＜i＜M1-1)，此时任务执行，且Eq={Nak,sk,nq}；

② 若Nak＞N0，即Ak在Bk的时间左侧(较Bk早)，则将Ak与b0对应项比较，若Lk≤η0，则任务执行，且Eq={Nak,sk,nq}；若Lk＞η0，将Ak与b1对应项Lk和η1重新比较，直到找到执行的时间，且得到Eq；

③ 若Nj＜Nak＜Nj+d，其中0＜j＜M1,d≥1，即Ak落在Bk中第j个元素时间右侧、第j+d个元素时间左侧，则将Ak与bj对应项Lk和ηj比较，若Lk≤ηj，则任务执行，且Eq={Nak,sk,nq}；若Lk＞ηj，将Ak与bj+d对应项Lk和ηj+d比较，直到找到执行的点，且记录Eq；

④ 如在步骤②、步骤③中出现执行时间Nk＞Nak+Wk，即执行任务的时间超出了预执行矩阵的最大时间窗，则任务Ak执行失败；其他情况下q=q+1。

5)k=k+1。若k=M1-1，则所有任务结束，转向步骤6)；否则转向步骤3)。

6)输出实际执行任务矩阵Eq。

上述过程的流程图如图3所示。

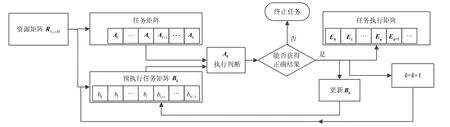
图3 调度算法执行流程图

2.4 性能分析

为了更好地评价算法执行情况，需要定义部分参数与指标。其中一类表示与仿真环境有关的参数，另一类为算法的评价指标。仿真参数主要包括“任务密度”和“任务平均生存期”。

1)任务密度。描述单位时间到来的任务对系统资源的占用情况，用λ表示为：

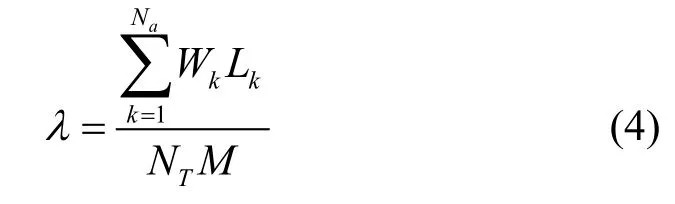
即用所有到来任务的占用资源(时间和孔径的乘机)除以总的时间孔径资源。显然，任务密度λ越大，系统资源占用率越高，则系统处理的难度越大，越对任务调度算法的效率有要求。

2)任务平均生存期。算法除了受到任务到达密度λ的影响，任务种类和任务生存期也能对执行结果造成影响(任务种类在仿真实验时设置)。理论上越大，系统可执行的任务越多。为：

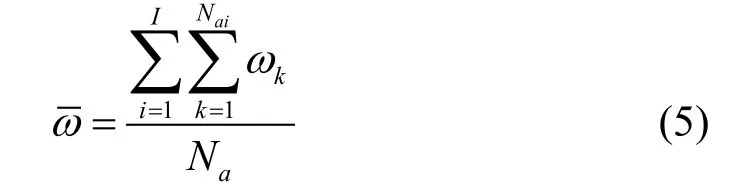
定义以下两个评价指标：

1)任务丢失率。表示未能执行的任务数在总任务数中所占的比例，反映了任务调度算法的执行效率，是多任务资源调度系统的重要指标。借鉴文献[11]的定义，执行失败的任务数与所有到来任务数的比值，即N2/(N-1)。显然在有限的时间资源下，任务密度对任务丢失率的取值有很大影响。一般来说，任务密度越大，任务执行失败的可能性越大，任务丢失率越高。

2)资源利用率。在常规雷达资源调度算法定义的时间利用率基础上，定义综合资源利用率，即在任务执行阶段对系统时间、孔径资源总的占用情况为

3 仿真分析

按照第2节的模型建立要求，首先需要设置天线的资源矩阵RNT×M和任务向量Ak。仿真采用线性阵列，子孔径数M=8，任务最小执行间隔为1 ms，调度时间为T=600 ms，调度的“时间片段”数NT=600。考虑到多功能相控阵天线执行任务类型的不同，需要对不同任务进行定义。将一体化电子系统的任务划分为雷达搜索A、雷达跟踪B、雷达成像C、语音通信D、数据通信E等5种类型(Kind)，定义其执行时间长度Wk、任务生存期ωk和占用孔径资源大小Lk等3种属性及对应数值如表1所示。这些任务属性、数值借鉴参考文献[12,16]给定的指标。考虑到本文主要处理的是任务调度算法，这些指标的具体数值不影响本文的基本结论。

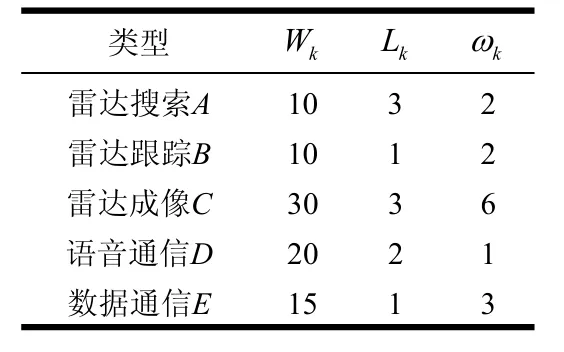
表1 任务类型定义

另设实际执行的任务序列为随机到达的，在NT=600个时间片内，总任务数600，A、B、C、D、E这5类任务的比例为10：5：1：5：2.5，计算任务密度得λ=1.1。将上述任务随机排序后分配到整个时间序列中。图4给出了单次执行前50个时间片的结果，并以第2节中提到的随机孔径策略作为对比。其中，纵坐标为天线孔径，横坐标表示时间。从中可以看出，本文所提方法的资源利用率较高。

图4 前50个时间片调度结果

表2 前100个任务的不同算法执行情况

对这两种方法分别进行500次蒙特卡洛仿真，执行结果可以得到表2。可知本文算法的任务丢失率显著低于随机孔径策略，而资源利用率大大高于后者。这是因为随机孔径策略没有进行优化，不少任务由于超过生存期，不能进入执行流程而死亡了。

进一步考察算法随着任务密度λ的增长(通过调整输入任务总数)执行情况，仿真为随机100次的平均值。从图5可以看出，对于两种方法，随着任务密度的增大，任务丢失率不断增大。如当λ=1时，随机孔径策略已经出现了约0.4的任务丢失率，此后任务丢失率基本呈现线性上升。但当λ＞1时，本文算法的任务丢失率同样增长很快。这是因为此时任务输入太多，远远超出了系统的调度能力，采用优化的方法也不能解决调度问题了。

与任务密度λ类似，任务平均生存期可能对算法有效性产生不同影响，即算法评价需要同时考虑λ和这两个参数的取值。将λ设置为从0.1到3的渐增值，从2到30，每一组参数执行20次，统计结果如图6所示。可以看出，任务密度λ越小、任务平均生存期越长，任务丢失率越小；当任务密度很低时，任务全部执行完毕，任务平均生存期基本不影响任务丢失率；反之，任务密度λ很高的情况下，只要任务平均生存期够大，仍然能够获得较低的任务丢失率。

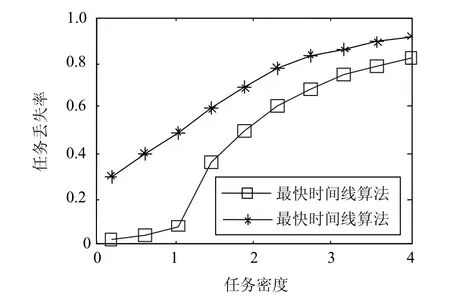
图5 任务丢失率比较

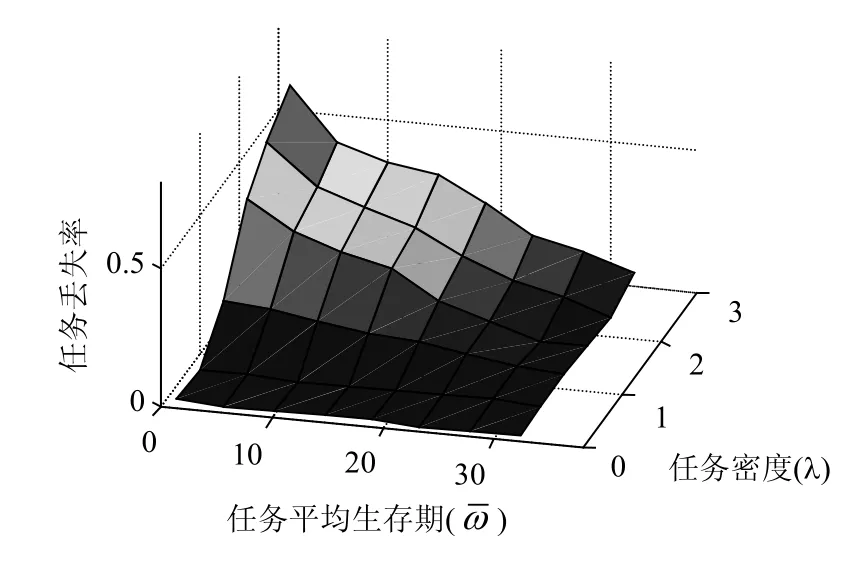
图6 不同任务密度和生存期下的任务丢失率

4 结 束 语

一体化的电子系统共同占用了平台的能量、时间和频谱资源，需要应对和处理的任务复杂多样，建立在孔径分割技术基础上的任务优化调度方法为合理分配系统资源提出了新的解决方案。本文首先分析并验证了相邻子孔径才适合执行同一任务的设定，提出了雷达通信一体化系统动态孔径分割条件下的时间、孔径二维的资源管理问题，并根据FIFO原则提出适合该问题的任务调度算法。事实上，按照FIFO的原则得到的方案是一种局部优化方法，不一定是最优调度方案。下一步将借鉴遗传算法、粒子群算法等对算法进行改进。

[1]张明友. 雷达-电子战-通信一体化概论[M]. 北京： 国防工业出版社, 2010.ZHANG Ming-you. Introduction of radar, electronic warfare and communication integration[M]. Beijing： National Defense Industry Press, 2010.

[2]刘永军, 廖桂生, 杨志伟, 等. 一种超分辨OFDM雷达通信一体化设计方法[J].电子与信息学报, 2016, 38(2)：425-433.LIU Yong-jun, LIAO Gui-sheng, YANG Zhi-wei, et al. A super-resolution design method for integration of OFDM radar and communication[J]. Journal of Electronics &Information Technology, 2016, 38(2)： 425-433.

[3]梁百川. 电子战装备一体化技术[J]. 信息与电子工程,2010, 8(4)： 397-400.LIANG Bai-chuan. Electric warfare equipment integration technology[J]. Information and Electronic Engineering,2010, 8(4)： 397-400.

[4]唐小明, 朱洪伟, 刘志坤, 等. 雷达通信一体化发展概述[C]//中国电子学会第十六届信息论学术年会. 北京： 电子工业出版社, 2009.TANG Xiao-ming, ZHU Hong-wei W, LIU Zhi-kun, et al.Overview of radar communication integration development[C]//The 16th Information Theory Conference of CIE.Beijing： Publishing House of Electronics Industry, 2009.

[5]TAVIK G C, HILTERBRICK C I, EVINS J B, et al. The advanced multifunction RF concept[J]. IEEE Transaction on Microwave Theory and Techniques, 2005, 53(3)： 1009-1020.

[6]秦童, 戴奉周, 刘宏伟, 等. 单波束相控阵雷达的时间资源联合分配算法[J]. 西安电子科技大学学报, 2016, 43(5)：1-6.QIN Tong, DAI Feng-zhou, LIU Hong-wei, et al. Time resource allocation strategy for single beam phased array radar[J]. Journal of Xidian University, 2016, 43(5)： 1-6

[7]叶朝谋, 丁建江, 俞志强. 基于周期分区的相控阵雷达任务交叉调度研究[J]. 电子与信息学报, 2014, 36(2)： 435-440.YE Chao-mou, DING Jian-jiang, YU Zhi-qiang. Study on task interleaving scheduling of phased array radar based on period division[J]. Journal of Electronics & Information Technology, 2014, 36(2)： 435-440.

[8]李秀良, 付林. 舰载一体化多功能雷达系统多功能集成与资源管理技术研究[J]. 雷达与对抗, 2010, 30(3)： 7-9.LI Xiu-liang, FU Lin. Multi-function integration and resource administration technology research of sea-based multi-function radar system[J]. Radar and Electronic Warfare, 2010, 30(3)： 7-9.

[9]卢建斌. 相控阵雷达资源管理的理论与方法[M]. 北京：国防工业出版社, 2010.LU Jian-bin. Resource management theory and method of phased array radar[M]. Beijing： National Defense Industry Press, 2010.

[10]CHEN Y J, ZHANG, Q, YUAN N, et al. An Adaptive isar-imaging-considered task scheduling algorithm for multi-function phased array radars[J]. IEEE Transactions on Signal Processing, 2015, 63(19)： 5096-5110.

[11]陈骋, 马晓岩, 杨瑞娟, 等. 基于遗传算法的多功能电子系统任务调度[J]. 现代防御技术, 2013, 41(4)： 68-73.CHEN Cheng, MA Xiao-yan, YANG Rui-juan, et al.Research of multi-functional electronic system task scheduling based on aperture partition[J]. Journal of Air Force Radar Academy, 2012, 26(6)： 412-418.

[12]綦文超, 杨瑞娟, 李晓柏, 等. 多功能一体化雷达任务调度算法研究[J]. 雷达科学与技术, 2012, 10(2)：150-155.QI Wen-chao, YANG Rui-juan, LI Xiao-bo, et al. Research on task scheduling algorithm for multifunction integrated radar[J]. Radar Science and Technology, 2012, 10(2)：150-155.

[13]赵长名, 刘健, 李云继, 等. 基于改进虚拟机整合算法的虚拟资源管理工具[J]. 电子科技大学学报, 2016, 45(3)： 355-360, 480.ZHAO Chang-ming, LIU Jian, LI Yun-ji. Virtualization resource management tool based on improved virtual machine consolidation algorithm[J]. Journal of University of Electronic Science and Technology of China, 2016, 45(3)： 355-360, 480.

[14]WEI L J, OON W C, ZHU W B, et al. A skyline heuristic for the 2D rectangular packing and strip packing problems[J]. European Journal of Operational Research,2011, 215(2)： 337-346.

[15]STOYAN Y, PANKRATOV A, ROMANOVA T. Cutting and packing problems for irregular objects with continuous Mathematical rotations： Modelling and non-linear optimization[J]. Journal of the Operational Research Society, 2016, 67(5)： 786-800.

[16]蒲小勃. 现代航空电子系统与综合[M]. 北京： 航空工业出版社, 2013.PU Xiao-bo. Modern avionics system and integration[M].Beijing： Aviation Industry Press, 2013.