太赫兹频段微动特征边缘检测及提取方法

田 坤，李 晋

(电子科技大学电子工程学院 成都 611731)

太赫兹频段电磁波是指频率在0.1～10 THz，即波长为30～3 mm范围内的电磁辐射。太赫兹雷达大带宽、高频率等技术特点可以有效提高雷达系统对微动目标的探测精度[1]。此外，与红外线和毫米波等相比，太赫兹波在散射、传播、吸收、反射和穿透等方面都具有明显的优势。

从2000年起，欧美国家相关研究机构就相继开展了关于微动目标雷达探测的研究工作。文献[2]率先提出了微多普勒的概念，将目标回波内雷达频率调制称为微多普勒效应，他对直升机的微动特征进行估计得到旋翼的几何结构和运动参数，从而实现了直升机的动态识别[3]。2002年，文献[4]运用全相参X波段连续波雷达获取人体行走微动数据，用于步态识别研究。2004年，文献[3]研究了人体走动中胳膊和腿的摆动带来的微多普勒调制，运用一台小型X 波段雷达探测人体走动并运用时频分析手段提取微多普勒特征。2007年，文献[5-6]通过雷达测量行人获取大量实测数据，结合小波分析与时频分析算法提取人体目标微多普勒特征，并利用微多普勒特征精确估计出微动参数。文献[7]针对传统时频分析方法对非平稳信号处理存在的缺陷，引入Hilbert-Huang变换分离噪声和微动信号，有效地改善微动模式的识别效果。2014年，文献[8]利用逆radon变换对时频谱中的微动特征参数进行提取。文献[9]利用微动特征提取对无人机旋翼目标展开特征识别。2015年，文献[10]利用微动信息开展空间目标的高分辨率三维成像技术研究。文献[11]利用微动特征开展了微动目标检测技术研究，上述这些检测和成像算法的性能好坏均取决于微动特征参数估计的准确与否。

然而，上述微动目标的探测与特征提取均仅建立在传统微动信号处理层面，导致其在多散射中心情况下的微动特征信号分离及参数提取性能较差。本文拟在微动特征模型的基础上，结合信号模型与图像处理的方法，对微动特征进行提取，进一步改善多散射中心情况下的微动特征参数的提取性能。

1 典型微动特征模型及参数

振动模型是一种典型的微动模型，弹簧振子的振动、甚至发动机的机械振动都可以用振动模型来近似。振动模型具有周期性。图1示出了雷达和振动质点的几何关系。

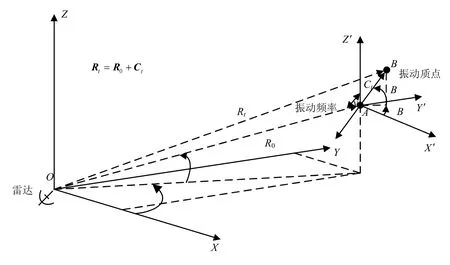
图1 雷达和振动质点的几何关系

雷达位于坐标系(X,Y,Z)的原点，振动的目标可以看作一个质点，质点以点A为振动中心以固定的频率ωv作振动，与雷达的距离为R0，A点在坐标系中方位角和俯仰角分别为α和β，再以质点振动中心A为原点建立坐标系(X′,Y′,Z′)，在该坐标系下，当质点振动至B点时，其位移为Ct，此时质点的方位角和俯仰角分别为αB和βB。此时，雷达的接收信号可以用下式表示：

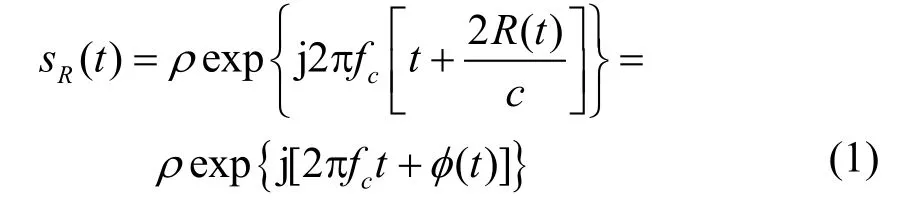
式中，ρ为目标点的反射率；fc为信号载频；φ(t)为相位函数：

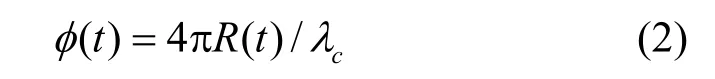
对时间求导，得到多普勒频率：

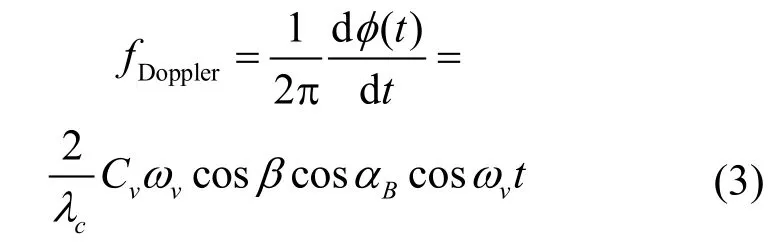
图2为具有4个振动部分和1个平动部分的复杂目标回波信号仿真。从图中可以看出，振动目标的回波信号呈典型的正弦特征。

此外，典型的雷达微动特征还有旋转、翻滚等等，它们的特征模型均可由振动模型推导。

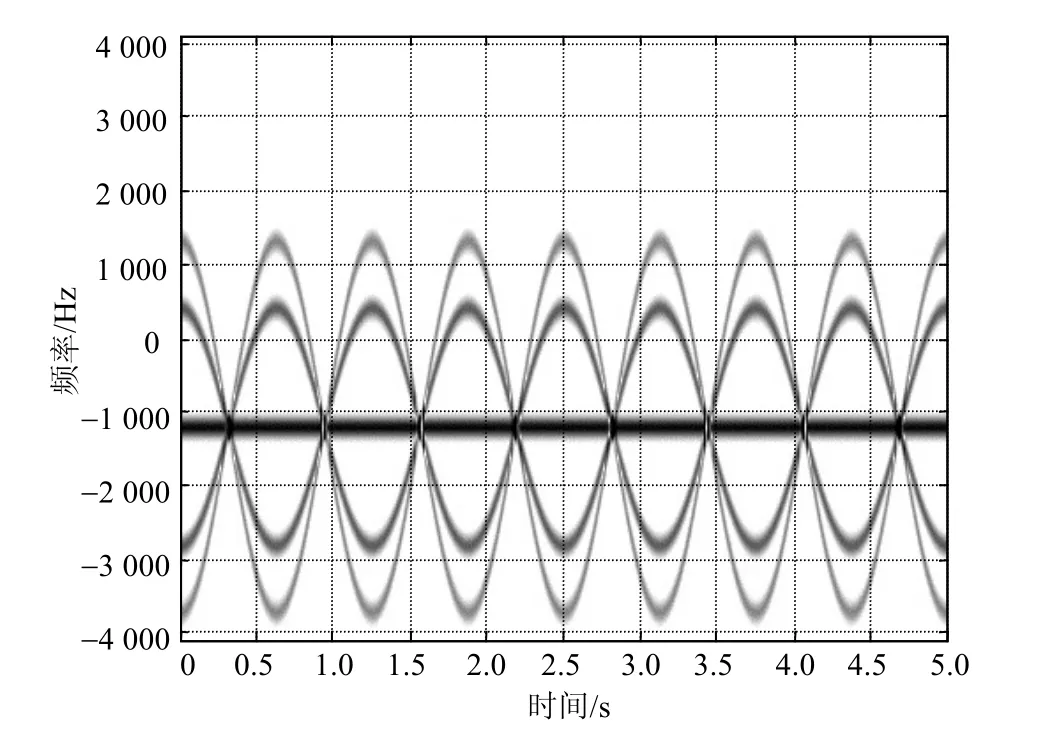
图2 复杂运动目标回波信号仿真

2 基于边缘检测的微动参数提取

由于微动目标回波信号是典型的非平稳信号，通常情况下采用时频分析的方法获得信号的时频谱，通过时频谱上对频谱曲线进行提取获取目标微动特征的相关参数。常见的时频曲线提取方法有脊线提取与质心曲线提取两种。

对于时频谱来说，在每个时间点的列上都会有一个最大值，脊线就是把每个时间点对应的列上的最大值作为该时刻的频率值，然后将这些点相连得到一个以时间为变量的函数，以该函数近似即时频率曲线。时频谱脊线可以由下式得到：

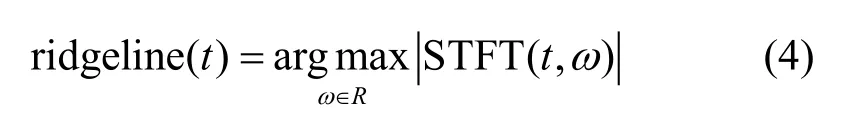
如果对每个时刻都选取整个频率范围内求加权平均值，每个时刻计算的平均值所对应的频率值即为该时刻的频率，这就是时频谱质心曲线提取方法。时频谱质心曲线可由下式得到：

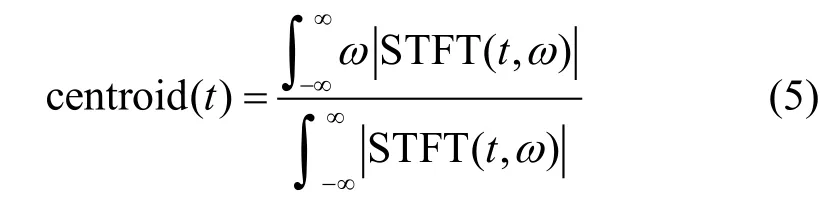
然而，这两种传统算法只能提取单一曲线，为了能同时提取出多条时频谱曲线，本文提出了一种基于边缘检测的时频谱曲线提取方法。其算法流程如图3所示。

图3 基于边缘检测的时频谱曲线提取算法流程

1)对回波的时频谱二值化处理。

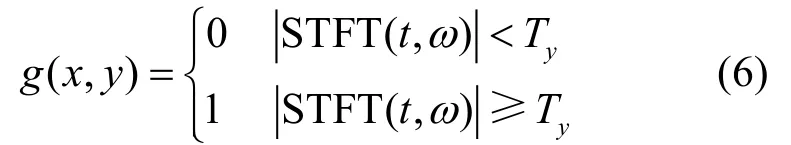
其中x与时频谱中的频率值ω对应，y与时间t对应，Ty为阈值。

图4示出了图2中无噪声情况下两种回波时频谱的直方图，该直方图显示了场景与目标回波强度之间的对比关系，便于对阈值进行选取。

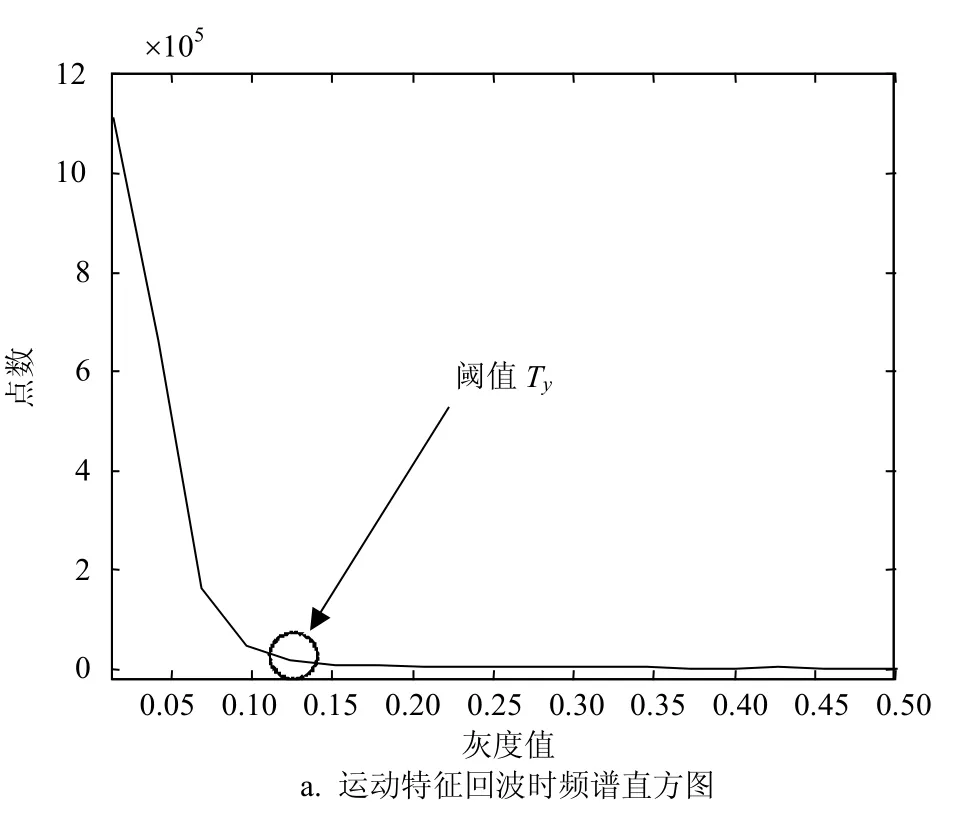
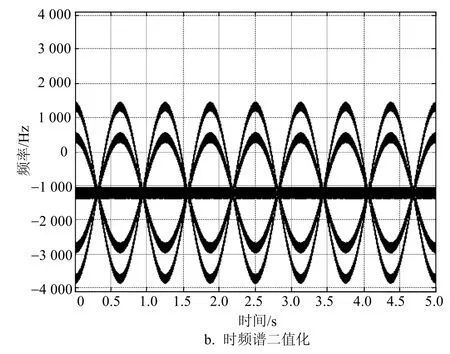
图4 回波频谱的直方图及其二值化结果

2)对时频谱二值化的结果g(x,y)进行边缘检测。

对于时频谱来说，每一列有其特殊的意义，即每一列代表一个时刻该信号的频谱，因此对时频谱按列进行边缘检测才有意义，所以文本选用列向量[-1,1]′作为边缘检测算子对步骤1)中二值化的时频谱进行边缘检测，其结果如图5所示。

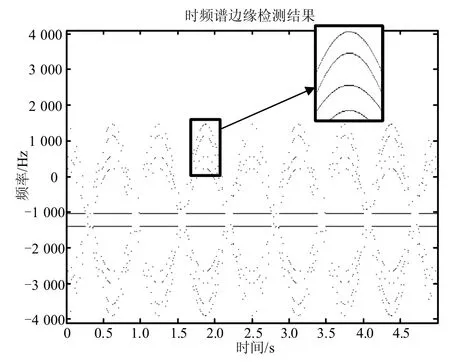
图5 回波频谱的边缘

3)将每个频谱条带的边缘合并至中心位置，得到时频谱曲线。

由于使用的边缘检测算子是按列卷积，所以每列的点数均为偶数，且两两一组，因此大大简化了对频谱中心的提取，将每组的两个边缘点对应的频率ω1,ω2找出，再求在该时刻两个频率的加权平均值即为即时频率。为了简化算法可以直接用ω1,ω2的平均值代替，得到时频谱曲线点的矩阵h(x,y)。图6显示出了将边缘合并为曲线的结果。

4)删除部分曲线点，减小曲线点的结果中噪声的影响。

从图6可以看到，曲线点基本上都集中在时频谱条带的范围内。但是在有噪声的情况下，除了相对集中的时频谱曲线点外，还有一些噪声带来的点会分散在其他频率，因此需要去除这些相对分散的点，以减小噪声的影响。可以用图6的曲线点或者图4时频谱二值化后的结果进行统计。

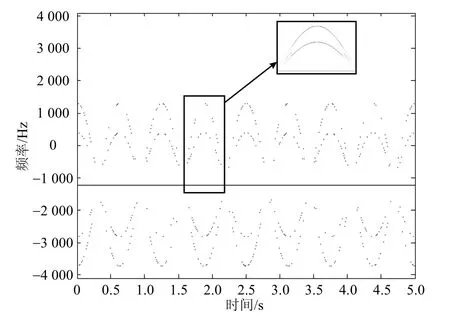
图6 回波频谱曲线点

5)对步骤4)的结果h(x,y)进行Hough直线检测。

Hough直线检测得到的参数如图7所示，该直线反应了主体运动的信息。由于微动是围绕主体运动进行的，其时频谱也围绕主体运动，所以在进行下一步时，要先对h(x,y)进行校正，将其每列都以直线点对齐，以便对曲线参数的检测。

6)对h(x,y)进行曲线检测。

时频谱曲线含有频率、幅度和相位参数，所以设置频率、幅度和初相的参数空间(f,A,θ)，参数空间中的每一个点(fi,Aj,θk)代入运动曲线模型：

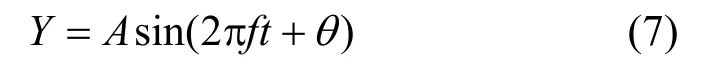
再将h(x,y)中所有的点进行计算，若符合该参数空间点建立的上述模型，则对该参数空间点进行累加，得到整个参数空间的累加值再找出累加器中的局部最大点对应的坐标位置，其对应的3个参数，即反应了每条曲线的频率、幅度和初相的参数。图7给出了参数空间的累加情况及其对应的参数。

再根据直线和曲线的参数将曲线转化为关于时间的函数，得到多条时频谱曲线，如图8所示。

上图提取的即为图2的运动回波时频谱的曲线，可以看到，原时频谱中的5个条带对应的曲线都被很好地提取出来。每条曲线都对应了目标的一个微动散射中心，对这些曲线进行分析就能得到具体的微动参数。

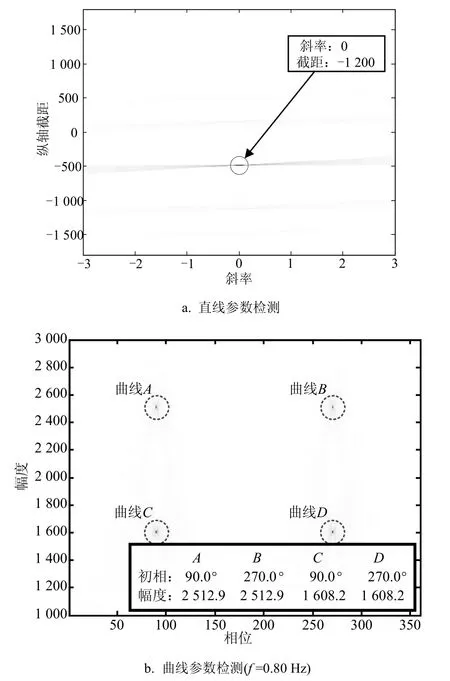
图7 直线和曲线参数检测结果

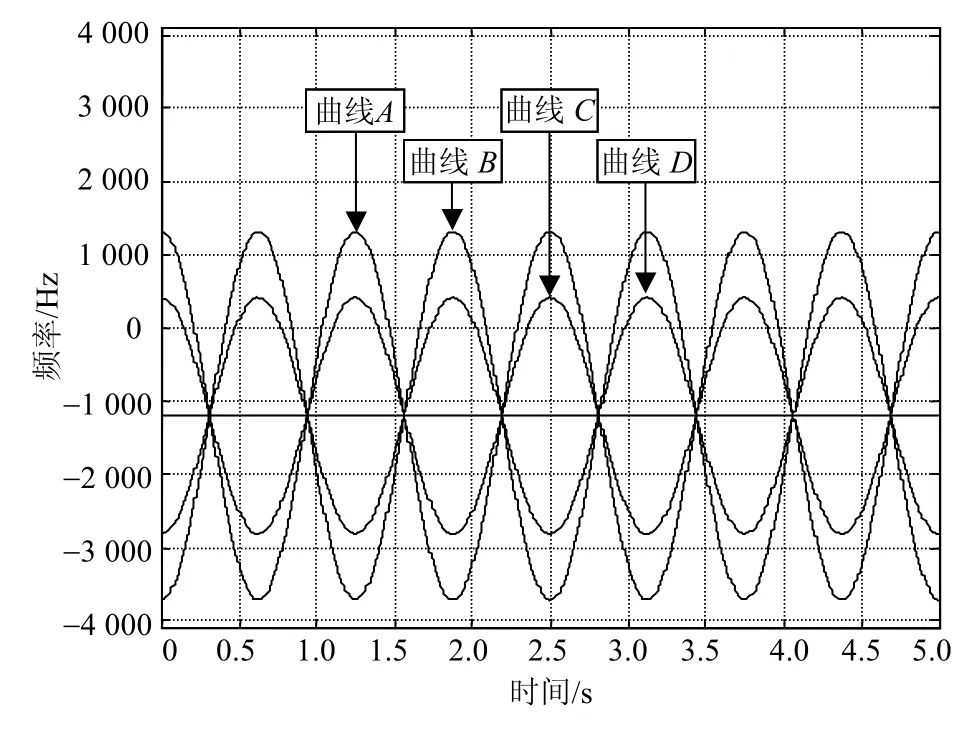
图8 运动回波时频谱曲线

对于这种有多个散射中心的情况，由于其回波的时频谱中每个中心都应该对应一条曲线，而传统的脊线和质心曲线方法都只能从一个时频谱图像中提取出一条曲线。因此若使用传统的曲线提取方法，则无法得各微动部分的时频谱曲线，其脊线提取和质心曲线提取的结果如图9所示。

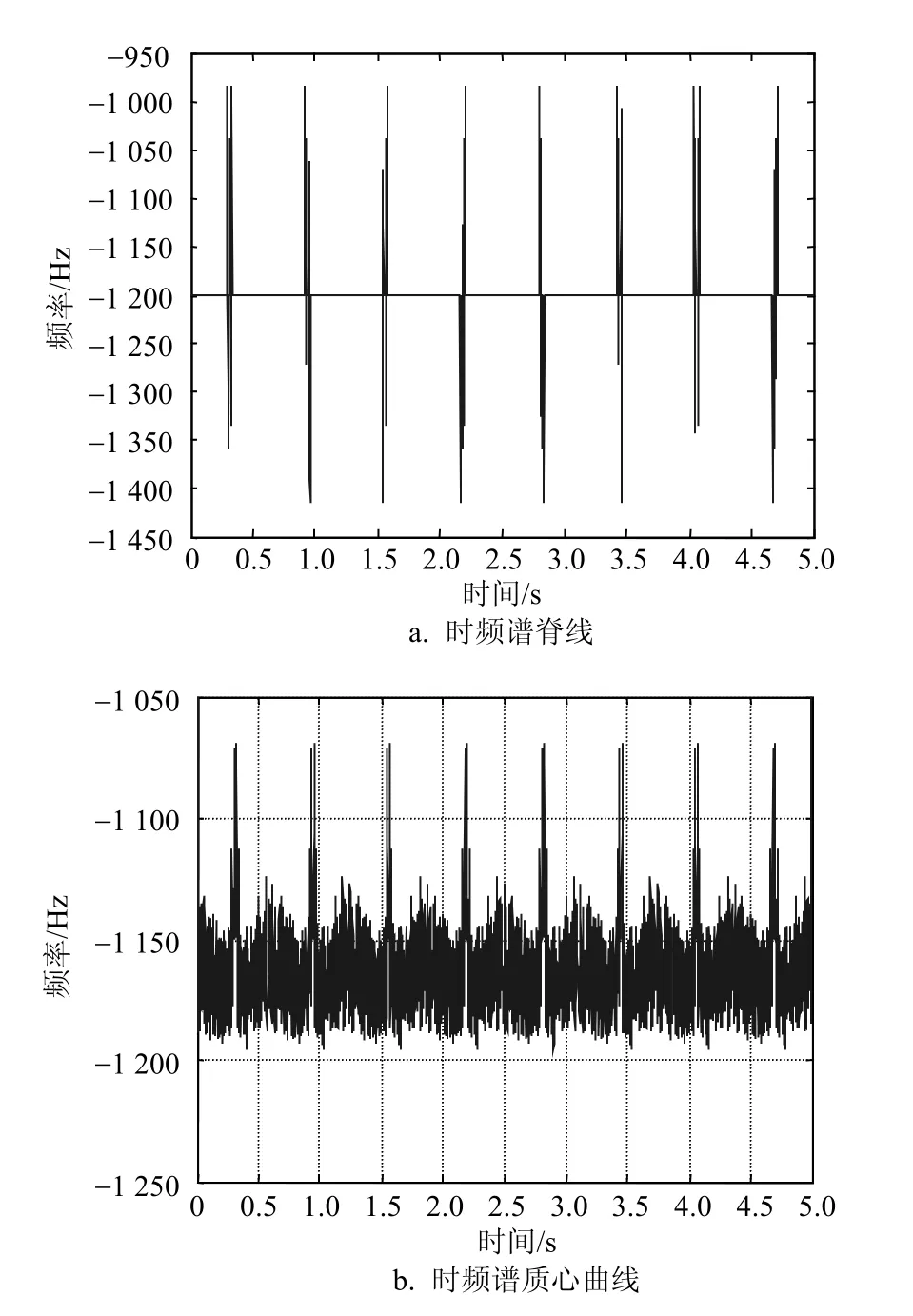
图9 目标回波时频谱的脊线和质心曲线提取

可以看出，基于边缘检测提取时频谱曲线的方法可以同时对多条曲线进行提取，克服了脊线提取和质心曲线提取这两种方法的缺点。

3 实验及结果分析

实验使用的太赫兹雷达系统实物图如图10所示。

图10 0.3 THz雷达系统实物图

雷达系统发射信号的中心频率在0.3 THz附近，信号带宽10.08 GHz，调频斜率3.36×1013Hz/s，发射脉冲信号的宽度300 μs，脉冲周期为1 ms。本文选取了单摆小球去近似人体模型进行实验。实验场景及示意图如图11所示。

图11 实验场景及示意图

可以看出，目标有横杆和小球两个散射中心，场景中各参数在示意图中示出，其中横杆的半径约为rg=1.2 cm，小球的半径为rb= 0.8 cm，摆长为l=57 cm，摆角为θ= 9o，小球在最低点时与雷达的距离为R= 6 m，这里以小球在最低点时作为参考点，参考距离Rref= 6 m。

由单摆周期公式计算可得，单摆的周期：

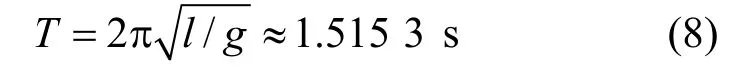
横杆高度为l+rg= 58.2 cm，与相对于参考点与雷达的距离差：

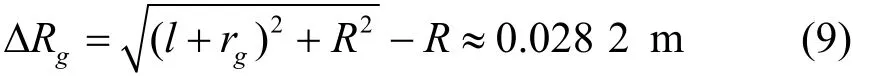
小球在最高点时，与雷达的水平距离Rx=R-lsinθ≈5.910 8 m，垂直方向距离为Ry=l(1-cosθ)≈0.007 0 m，所以在最高点小球与雷达距离为此时，小球相对于参考点与雷达的距离差为：

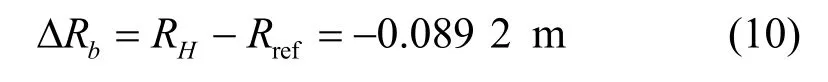
图12示出了单个小球实验的回波时频谱。

得到其时频谱曲线后，即可算出目标的即时距离及其他微动参数。结果如图13所示。

直接提取出的参数与模型计算的参数对比于表1和表2中。

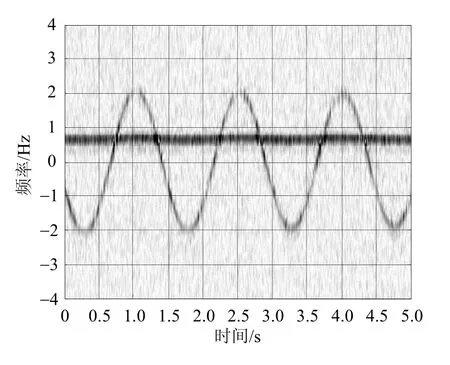
图12 回波时频谱及二值化

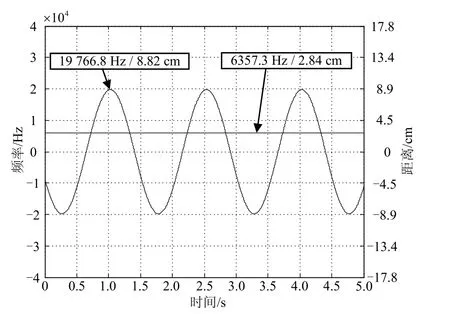
图13 提取出的曲线

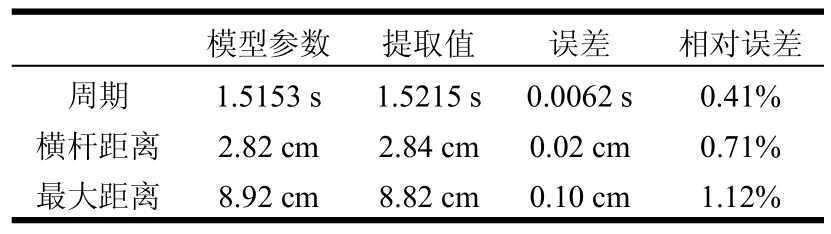
表1 目标微动提取参数对比

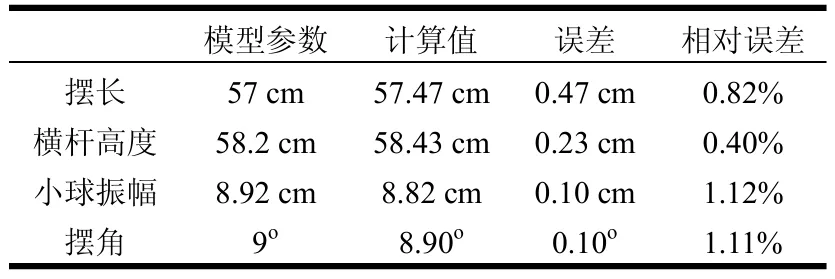
表2 计算获得的参数对比

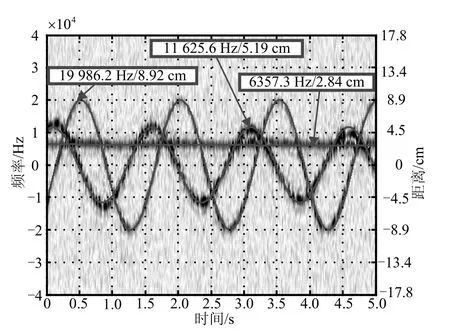
图14 两个小球实验场景及曲线提取结果

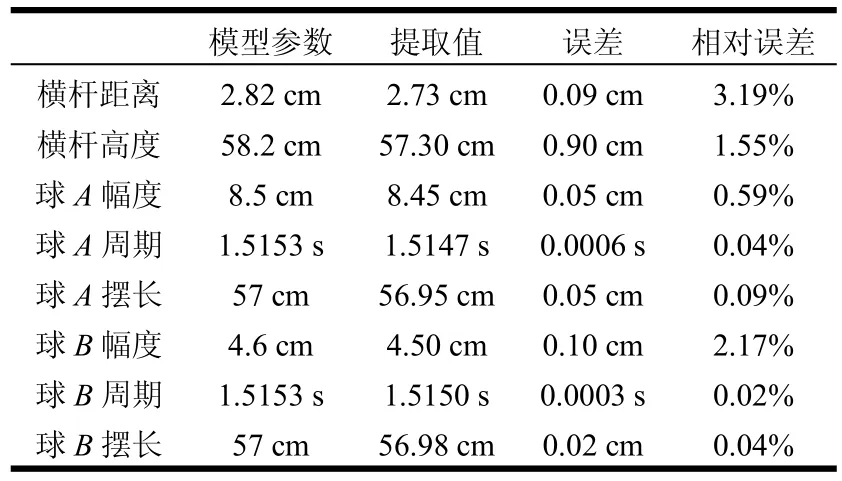
表3 两小球参数设置与提取结果对比

从上面的数据及分析可以看到，无论是直接提取的参数还是根据提取值进行进一步理论推导获得的计算值，都与初始设置的模型参数基本一致。该实验在验证了该方法的可行性的同时也说明了该方法在太赫兹雷达下对目标微动参数提取具有较高的准确性。

4 结 束 语

本文采用了一种基于图像处理的微动特征边缘检测技术，该方法可结合微动特征信号模型进行微动特征曲线及参数提取。实测数据表明，该方法具有较好的性能，能有效提取多散射中心微动目标的特征参数，为进一步开展微动信号处理及目标识别提供了有效的技术途径。

[1]LI J, PI Y. Micro-doppler signature feature analysis in terahertz band[J]. Journal of Infrared, Millimeter, and Terahertz Waves, 2010, 31(3)： 319-328.

[2]CHEN V C. Analysis of radar micro-doppler signature with time-frequency transforms[C]//Proceedings of the 10th IEEE Workshop on Statistical Signal and Array Processing.Pocono Manor, USA： IEEE, 2000.

[3]CHEN V C, LI F Y. Micro-doppler effect in radar-phenomenon, model and simulation study[J]. IEEE Trans on Aerospace and Electronic Systems, 2006, 43(1)：2-21.

[4]GEISHEIMER J L, GRENEKER E, MARSHALL W S. A high-resolution Doppler model of human gait[C]//Proceedings of SPIE on Radar Technology. [S.l.]： SPIE,2002： 8-18.

[5]THAYAPARAN T, ABROL S, RISEBOROUGH E.Micro-Doppler radar signatures for intelligent target recognition[R]. Ottawa, Canada： Technical memorandum DRDC Ottawa, 2004.

[6]THAYAPARAN T, ABROL S, RISEBOROUGH E, et al.Analysis of radar micro-Doppler signatures from experimental helicopter and human data[J]. IET Radar Sonar Navigator, 2007, 1(4)： 289-299.

[7]LAI C P, RUAN Q, NARAYANAN R M. Hilbert-Huang transform (HHT)processing of through-wall noise radar data for human activity characterization[C]//IEEE Workshop on Signal Processing Applications for Public Security and Forensics. [S.l.]： IEEE, 2007： 1-6.

[8]QI Y, BIN D, HONGQIANG W, et al. Doppler aliasing free micro-motion parameter estimation algorithm based on the spliced time-frequency image and inverse Radon transform[C]//International Conference on Information and Communications Technologies. Nanjing： [s.n.], 2014.

[9]TAHMOUSH D. Detection of small UAV helicopters using micro-Doppler[J]. Proceedings of SPIE-The International Society for Optical Engineering, 2014, 9077(18)： 5450-5453.

[10]BAI X, ZHOU F, BAO Z. High-resolution threedimensional imaging of space targets in micro motion[J].IEEE J Sel Topics Appl Earth Observ Remote Sens, 2015,8(7)： 3428-3440.

[11]LI J, PI Y. Target detection for Terahertz radar networks based on micro-Doppler signatures[J]. International Journal of Sensor Networks, 2015, 17(2)： 115-121.