基于自适应同时稀疏表示的鲁棒性目标追踪

李厚彪，樊庆宇，耿广磊

(电子科技大学数学科学学院 成都 611731)

目标追踪在计算机视觉领域占据着重要的地位。目标追踪的主要任务包括：感兴趣运动目标的检测、视频帧到帧之间的连续追踪和追踪目标的行为分析等[1-2]。

当前目标追踪所面临的一些挑战主要包括光照变化、背景混杂、部分遮挡、完全遮挡以及它们的混合。为了解决这些问题，各种不同的追踪算法相继被提出来，如在线学习方法(online learning)和基于稀疏表示(sparse representation)的追踪算法。在线学习方法大致又可分为：生成方法(generative approaches, GA)和判别方法(discriminative approaches, DA)。GA是一种搜索与追踪目标最相似的区域方法，如文献[3]使用积分直方图的健壮片段跟踪，减弱了部分遮挡和姿势变化等因素对追踪效果的影响，有效降低了计算代价；另外，为更好地实现鲁棒性追踪，基于增量学习的目标追踪算法[4]和基于核的目标追踪算法[5]相继被提出来。尽管生成方法在一定程度上能实现追踪，但是不能有效解决长时间部分遮挡、完全遮挡、目标外形剧烈变化等追踪问题。DA可看作是一种二分类问题，主要利用已知的训练样本训练出一个分类器，用于判别目标和背景。文献[6]提出在线多实例学习的目标追踪算法，该方法不同于传统的监督学习方法，主要区别为用于训练时的阳性样本(positive sample)数量大于阴性样本(negative sample)数量；文献[7]提出超像素追踪方法，该法使用超像素特征的结构信息能更好判别目标和背景，在一定程度上适应姿势改变、运动模糊及短时间的部分遮挡等情况，但该方法的计算代价较高且只用了简单的HIS颜色特征并未考虑更好的颜色特征；文献[8]提出基于核空间的稠密采样追踪算法，使用循环矩阵和快速傅里叶变换在核空间里实现了快速学习，大大提高了追踪系统的实时性。

文献[9]提出稀疏表示在人脸识别中的应用(sparse representation based classification, SRC)，对噪声污染和人脸部分遮挡获得较好的识别率，相比之前提出的SVM、KNN、PCA和LDA等线性分类器，不仅表现出更优的识别效果，且有更强的抗干扰能力。受其启发，文献[10]提出稀疏表示在目标追踪方面的应用，此后不断得到发展，如稀疏表示追踪[10-15](L1Tracker)、联合表示追踪[16](L2Tracker)、同时稀疏表示追踪[17](Lp,qTracker)、核稀疏表示追踪[18-19](KSR Tracker)和混合稀疏表示追踪[20-21]等。

本文提出了同时稀疏表示的自适应追踪算法，该算法采用子空间学习(subspace learning)和无监督学习(K-means)相结合的模板更新方法, 避免了模板更新太快而引入较大的误差；另外算法使用同时稀疏表示来刻画粒子之间的关系，克服了传统稀疏表示假设粒子之间是相互独立的缺陷；最后根据噪声(如遮挡，光照变化等)能量的大小自适应的选择模型。大量的实验结果表明该算法可实现鲁棒性追踪。

1 自适应同时稀疏追踪模型

1.1 同时稀疏Lp,q模型

目前，粒子滤波方法已被成功应用到目标追踪中：若追踪过程中第(t-1)帧的追踪目标状态为粒子则第t帧的追踪目标可能的状态记为且第t帧的观测为其中yt为第t帧的观测值。稀疏表示追踪给出了的具体形式，并根据最小重构误差得到目标的追踪结果yt。

式中，e表示高斯噪声；I表示琐碎模板。文献[15,22]提出的稀疏表示追踪模型为：

式中，D=[T,I]表示追踪模板；x=[z,e]T；λ表示正则参数，用来平衡保真项和正则项。若考虑粒子之间的关系，则可给出稀疏追踪模型[17]：

尽管上述模型在一定程度上解决了部分遮挡、光照变化、姿势改变和背景混杂等影响，但太过简单地考虑噪声的分布情况，因此面对一些复杂的噪声分布情况可能会出现跟踪失败。为此下面假设噪声服从高斯拉普拉斯分布，即：

式中，S表示拉普拉斯噪声；E表示高斯噪声。给出同时稀疏追踪模型：

式中，X=[Z,E]T。但对于一个给定的视频序列，目标并不总处于被污染状态，设已追踪到目标对应的拉普拉斯噪声为St(表示S的第t列)，因此可给出自适应的同时稀疏追踪模型为：

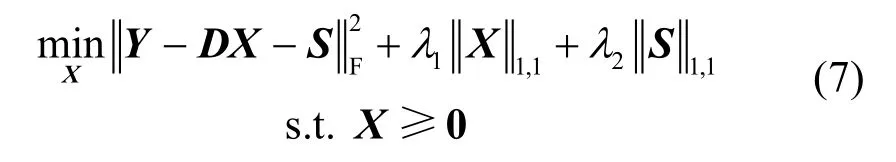
式中，τ为给定噪声能量的阈值；1λ和2λ为模型的正则参数，分别用来控制表示系数X的稀疏程度以及噪声S的能量大小。

模型求解：式(6)和式(7)的目标函数是一个凸优化。使用交替方向乘子方法(alternating direction method multipliers, ADMM)求解优化问题(7)如下：

首先，将约束问题变为无约束问题：

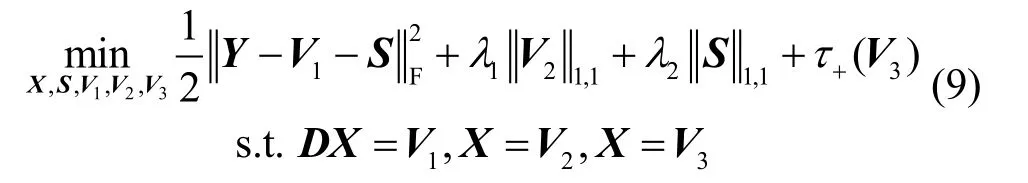
式中，V1,V2,V3为对偶变量，式(9)进一步优化为：

式(10)的增广拉格朗日函数为：

式中，β表示拉格朗日乘子；式(11)可分解为3个子优化问题：

因此根据极值原理，只需要对上述子问题求一阶导数，可获得式(11)的最优解：

同理，对于式(6)得到以下解：

这样通过对子问题的分析与求解，获得了式(6)和式(7)解的一般形式，数值求解见算法1和2。

算法1：问题(6)的ADMM求解算法

初始化：k=0，X(0)，Y，正则参数λ1，λ2，对偶变量拉格朗日乘子收敛误差ε，惩罚因子β。

输出：最优解(k+1)X

算法2：问题(7)的ADMM求解算法

初始化：k=0，X(0)，S(0)，Y，正则参数λ1，λ2，对偶变量拉格朗日乘子收敛误差ε，惩罚因子β。

输出：最优解X(k+1),S(k+1)

1.2 模板更新

模板更新的好坏直接影响追踪的性能。在稀疏追踪模型中提出了用目标模板和琐碎模板相结合的模板更新方法，对于每一个追踪的目标y，如果y与模板的相似性很高，则不更新，否则将y引入模板中并剔除模板中权重较小的向量。引入琐碎模板是为了更好地解决目标遮挡问题，这种模板更新方法虽然在一定程度上可以减弱跟踪漂移现象，但是模板维数较高，提高了模型的计算代价，从而降低了追踪系统的实时性。下面用子空间学习和无监督学习相结合的模板更新方法来降低模板的维数，并且能避免模板更新过快而引入较大的误差。

若给定当前模板T，已追踪到的目标y以及噪声能量相似度τ，则拉普拉斯噪声S=Y-TZ-E。如果则对模板T进行更新：首先分别对T和y进行奇异值分解：

进一步给出τ的等价定义,令c=mean(T)，则：

式中，τ等价为目标与模板均值的反余弦，即余弦夹角。文献[4]提出增量子空间学习追踪算法，同理可使用奇异向量u,s,v去增量更新U,S,V，从而得到新的奇异向量U*,S*,V*。新的模板可表示为：

考虑模板的维数较大，给定初始类个数为k，使用无监督学习K-means方法训练模板：

式中，i表示第i个样本；当Ti*属于类k时，rik=1，否则rik=0；uk为所有属于类k的样本的平均值。因此新的模板变为Tnew=[u1,u2,…,uk]。

本文提出的模板更新不同于传统的模板更新，它强调选择对目标追踪具有重要贡献的模板，而避免使用琐碎模板，并通过K-means算法对模板进行无监督训练，大大剔除了模板的冗余信息，从而提高了追踪的实时性。

1.3 追踪算法

在目标追踪过程中，假设第(t-1)帧的目标状态为qt-1，第t帧的所有观测为Yt。目标状态更新和观测更新可以表示为：

式中，状态qt由6个仿射参数决定且彼此之间相互独立，即qt=[tx,ty,θ,ε,μ,ρ]，θ、ε、μ、ρ分别表示旋转角度、规模大小、长宽比和倾斜度；[tx,ty]表示二维旋转参数；wt表示第t帧的粒子权重；表示第t帧的目标状态，可以由服从均值为qt-1、方差为δ2的高斯分布函数决定；而p(Yt|qt)可由同时稀疏L(p,q)的最小重构误差得到：

在实际中wt通过粒子滤波算法自适应更新得到，细节见文献[15]；方差δ=0.05，仿射参数由仿射矩阵逆变换得到。对应的自适应同时追踪算法，见算法3。

算法3：自适应同时稀疏追踪算法

输入：第t帧所有侯选粒子初始追踪目标模板Dt、最大迭代次数Loop、收敛误差tol、余弦夹角阈值α、正则参数λ1,λ2。

1)根据式(13)计算追踪目标yt与模板均值的相似性，记为sim

2)判断sim与α的大小，并自适应地选择模型进行追踪

3)IF sim＜α

4)选择算法1进行求解并获得稀疏系数矩阵X

5)ELSE sim≥α

6)选择算法2求解得到稀疏系数X和噪声S

7)根据式(12)，式(14)～式(15)自适应更新模板

2 实验结果

2.1 数据和实验说明

下面通过数值试验把本文提出的算法与其他5种具有很好追踪性能的算法进行比较，这5种追踪算法分别为核技巧的循环矩阵追踪(circulant structure of kernels, CSK)[8]、加速梯度追踪(accelerated proximal gradient, L1APG)[14]、多任务追踪(multi-task tracking, MTT)[17]、稀疏原型追踪(sparse prototype tracking, SPT)[23]以及稀疏联合追踪(sparse collaborative method, SCM)[21]。所有的实验均基于Matlab 2012a，计算机内存为2 GB，CPU为Intel(R)Core(TM)i3。实验数据来源于文献[20]。

本次实验选择了14种不同的具有追踪挑战性的视频，其中包括遮挡、光照变化、背景混杂、姿势改变、低分辨率和快速运动等影响追踪结果的因素，如表1所示。其中OV表示目标丢失，BC表示背景混杂，OCC表示完全遮挡，OCP表示部分遮挡，OPR表示旋转出平面，LR表示低分辨率，FM表示快速运动，SV表示大小变化。

在实验中参数设置如下： 正则参数λ1=0.1，λ2=0.1，惩罚因子β=0.1，余弦角度阈值αmin=20，αmax=35，模板最大基向量个数为15，粒子采样数为600，图像块的大小为25×25，实验最大迭代次数Loop=20。参数1λ,2λ均通过交叉验证方法得到，且2λ参数的调节满足如下规则，若噪声S的能量较大(即目标遭受较大的遮挡、外形变化或光照变化)，此时2λ的值应该较小，反之则较大。

表1 各种不同具有挑战性的追踪视频

2.2 评价准则

本文实验采用的评价方法有3种，且每种评价方法都能在一定程度上解释追踪性能的好坏，分别为局部中心误差(center local error)、重叠率(overlap ratio)、曲线下的面积(area under curve, AUC)。

给定帧的真实目标框Rg(ground truth)和追踪目标框Rt(tracked target bounding)，设它们的中心位置分别为：pg=(xg,yg)和pt=(xt,yt)，则局部中心误差为重叠率为：

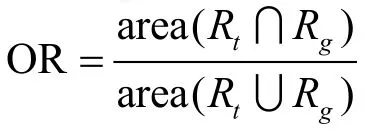
式中，area(⋅)表示在该区域的所有像素；AUC每一点的值表示重叠率大于给定阈值η时该视频追踪的成功率。特别地设定η=0.5，当重叠率OR＞0.5时则认为该帧追踪成功。相关追踪结果如表2～4所示，表2中AOR表示总的平均重叠率，表3中ACLE表示总的平均中心误差，表4中ASR表示总的平均成功率，表中最好的两个结果分别用红色和蓝色表示。各算法追踪性能如图1～3所示，图1中平均重叠率越大表示追踪性能越好，图2中平均中心误差越小表示追踪性能越好，图3中曲线与x轴围成的面积越大表示追踪性能越好。

表2 基于平均重叠率的各种不同算法性能的对比

(续表)

表3 基于平均局部中心误差的各种不同算法性能的对比

表4 基于平均成功率的各种不同算法性能的对比

图1 各种不同追踪算法的平均重叠率

图2 各种不同追踪算法的平均中心误差

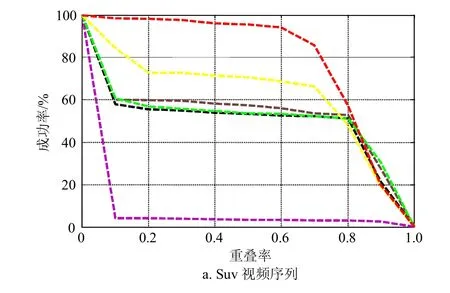
图3 各种不同追踪算法的AUC曲线

2.3 追踪结果分析

为了方便描述，将本文提出的追踪算法简记为ASSAT算法(adaptive simultaneous sparse representation appearance tracking algorithm)。

1)背景混杂和快速运动情形：图4分别给出了快速运动和背景混杂的追踪效果，视频Deer包含快速运动因素。从Singer2可看到大部分算法都无法有效追踪到结果，在帧240时，有很多算法的追踪框偏离目标，漂移现象很严重，如SCM，CSK，MTT，L1APG，SPT等，只有ASSAT算法可以有效追踪到目标。在帧366时(视频结束)本文提出的依然可以有效追踪到目标，大大减弱了追踪漂移现象。在视频SUV中，开始时所有追踪算法均能有效追踪到目标，在帧560时，只有SCM, CSK和ASSAT算法可以追踪到目标，在第945帧时只有ASSAT可以有效追踪到目标。对于视频Deer而言，可以看到除了MTT算法大部分算法均能有效追踪到目标，另外可以看到SCM算法不太稳定，因在帧40时SCM算法偏离了追踪目标，出现跟踪漂移现象。ASSAT算法可以有效追踪背景混杂的视频序列是因为其采用了同时稀疏表示方法，该方法通过模板基的选择来刻画粒子之间的关系，对噪声污染较大的粒子给与了较低的稀疏权重，因此具有很强的噪声抗干扰性。

图4 基于快速运动和背景混杂视频下的追踪效果

2)姿势改变和光照变化情形：图5和图6分别给出了姿势改变和光照变化的追踪效果。从图5中的Deduk视频可以看出所有的追踪算法都能有效追踪到目标(人脸)，但是ASSAT可以更加准确地追踪到人脸目标，而对于Skater2视频，大部分算法都无法准确跟踪到目标，因为目标姿势改变的太过频繁且改变的幅度较大，在第90帧时只有LIAPG, CSK和ASSAT算法可较为准确的追踪的目标，但在帧435时只有ASSAT和CSK能够追踪到目标，尽管追踪的不太精确。图6可以看到几乎所有算法都可以对光照变化产生一定的抗干扰性，除了LIAPG和CSK算法有一些不太稳定。因此对于姿势改变不大的情况ASSAT算法还是可以有效的追踪到目标。

图5 基于姿势改变和旋转视频下的追踪效果

图6 基于光照变化视频下的追踪效果

3)目标遮挡情形：图7展示了目标遮挡对跟踪性能的影响，在Girl视频序列中可看到在帧458和帧500时，大部分算法都出现了跟踪漂移现象，不能有效追踪到目标，除了ASSAT，LIAPG和MTT算法，从Subway也可看到在帧41时，只有SCM, L1APG和ASSAT算法可有效追踪到目标，而在帧175时，除了SCM和ASSAT算法其他算法都出现了很大的跟踪漂移。通过比较可看出ASSAT算法能更好的解决目标遮挡问题，这是因为该算法考虑了遮挡对追踪的影响，它就像一个滤波器在追踪之前对噪声进行了有效剔除，去除了可能对追踪效果产生影响的不稳定的因素(遮挡、光照变化、背景混杂和姿势改变等)。

图7 基于目标遮挡视频下的追踪效果

3 模型分析

下面详细介绍模型中提到的拉普拉斯噪声和模板更新准则对追踪效果的具体影响。

传统的模板更新方法是直接通过追踪目标与模板的相似度进行更新，若相似度大于给定的阈值，则认为目标遭遇了较大的噪声污染，因此需要将追踪目标替代原始权值较小的模板向量，这样替换其实是比较粗糙的，因为引入了较大的噪声误差，这样就给下一帧目标的追踪造成了很多不确定性，而本文提出的新的模板更新方法则削弱了噪声影响。具体表现如下：

1)新的模板更新方法有效权衡原始模板向量和新的追踪目标之间的权重，通过遗忘因子实现模板更新(具体见文献[4]);

2)新的模板更新方法引入了K-means方法，可以有效地降低冗余模板向量，提高追踪的实时性，通过式(18)可看到类中心的计算是通过加权平均得到的，因此也可有效地减弱噪声。

下面给出具体实验分别比较模板更新和拉普拉斯对实验效果的影响。实验数据选择序列Skater2，Dudek, SUV，Walking2，Subway，Deer等。

表5 比较拉普拉斯对实验结果的影响

从表5可以看出除了Walking2序列，加入拉普拉斯噪声后其追踪效果要优于MTT算法。但是原始模板更新的方法限制了它的追踪性能，而提出的新模板更新方法促进了ASSAT算法的追踪性能。

表6 比较模板更新对实验结果的影响

从表6中可以看出仅使用模板更新的ASSAT方法和IVT方法的追踪效果差不多，对于Skater2，Subway序列两种方法效果都不好，原因是这两种序列含有较大的遮挡，对于仅考虑模板更新而没有考虑拉普拉斯噪声的ASSAT算法是无法有效追踪到目标的，IVT也是一样。但两者结合会取得更好的追踪效果。事实上，对于这种含有较大遮挡的情况，若不考虑拉普拉斯噪声，可归结到噪声因素影响了式(5)中解X的稀疏结构，如图8所示。

图8 拉普拉斯噪声对解X的影响

图8表示目标在遮挡情况不同的情况下噪声选择对解的影响。图8的第一行表示考虑拉普拉斯噪声时所得到的解，可以看到解是稀疏的，此时解是最优的；图8的第二行表示未考虑拉普拉斯噪声时所得到解，此时解是稠密的，非最优解，因此保持解的稀疏结构直接影响算法的追踪性能。

4 模型的进一步改进

为了提高追踪系统的实时性，下面考虑自适应Lp稀疏表示目标追踪算法，该算法与前面提出的算法一样，也考虑了噪声分布的影响，且模板更新采用在线增量学习与K-means相结合的模板更新方法，唯一不同的是，模型中认为粒子之间的影响是相互独立的，可以分别通过稀疏模型进行求解，且使用了LASSO求解算法，根据粒子滤波框架理论和最大后验概率求出最优追踪结果。数值试验结果表明该算法相对于目前存在的较好的追踪算法取得了更好的追踪效果，表现为精确性更高、实时性更好。

4.1 自适应Lp模型的建立和求解

假设噪声分布服从高斯拉普拉斯分布：噪声n服从高斯分布噪声s服从拉普拉斯分布侯选目标y可以写成：

通常在噪声污染较小的情况下，认为侯选目标y可由模板T的少量基的线性组合来表示，这就意味着求解系数x是稀疏的，因此稀疏表示模型变为：

同前面分析一样，令：

式中，τ是一个阈值，当噪声能量大于τ时，此时需要考虑拉普拉斯噪声的影响，反之则忽略拉普拉斯噪声的影响。因此最终模型如下：

式(21)的求解可以采用交替迭代的方法，每一次迭代都使用一次LASSO算法，令：

式中，shrink是一个紧缩算子。

4.2 自适应Lp模型的追踪算法

目标状态的更新和预测是目标追踪算法的核心问题。前面介绍了增量学习与K-means相结合的模板更新方法，本节提出的算法依然采用这种模板更新机制。类似的给出了自适应Lp模型的追踪算法4。

算法4：自适应Lp模型追踪算法

输入：第t帧侯选粒子最大迭代次数Loop、收敛误差tol、阈值区间[α,β]、正则参数λ1、λ2。

1)初始化i=0，j∈[1,m]，拉普拉斯噪声

2)根据式(13)计算追踪目标yt与模板均值的相似性，记为sim

3)迭代

4)迭代直到i＞Loop 或者

6)通过式(12)～式(15)更新目标模板T，并得到新模板T*

输出：追踪目标yopt和新的模板T*

4.3 实验结果与分析

选取20种不同的视频序列(http：//cvlab. hanyang.ac.kr/trackerbenchmark/datasets.html)，实验中模板基的个数设定为15，最大迭代次数和收敛误差分别为Loop=5，tol=0.001，阈值区间α=20,β=28。使用LASSO算法[24]求解L1模型，在默认的情况下正则参数λ1=0.2，λ2=0.1，实际中通过交叉验证的方法可以设置参数λ2∈(0.000 5,0.5)。

将算法4和目前9种比较好的算法进行比较，除了前面的CSK算法[8]、L1APG算法[14]、MTT算法[17]、SPT算法[23]和SCM算法[21]、再增加DFT算法[25]、ORIA算法[26]、IVT算法[4]、ASLSA算法[7]。

表7和表8给出了在20种不同情境下的定量数据展示。表7中AOR表示平均重叠得分，Fps表示每秒追踪的帧数，Fps越大表示追踪的越快即说明该算法的实时性越好。本文提出的算法AOR=0.74和ACLE=6.5是最好的，而Fps=9.53排名第三，这表明算法4在保证追踪精度的同时实时性也较好。

表7 10种追踪算法的追踪性能的定量分析表

表8 10种追踪算法的ACLE比较

(续表)

图9展示了目标遭受快速运动、尺度变化和姿势旋转等噪声影响的追踪实验结果。对于视频Football，很明显本文算法可成功追踪到目标，其他算法都丢失了目标(见帧318和帧362)；对于视频Skater2，大部分算法都不能准确追踪到目标，在帧10时，每一种追踪算法都可以捕捉到目标，但在帧200时，因为目标形态改变太多，此时已经没有算法可以准确捕捉到目标了，在帧435时，只有本文的算法、CSK和ASLSA算法可以捕捉到目标的一部分；对于视频Deer和Surfer，可很清楚地看到本文的算法，SCM, SPT, ASLSA和L1APG算法可有效捕捉到目标。其原因归结于本文的算法综合考虑了噪声的影响，且将噪声部分进行很好地剔除，使得目标可以被模板稀疏表示，因而追踪成功。

在实验中所有的参数都通过交叉验证的方法得到，在追踪过程中参数λ1不灵敏，一般可据经验设置在区间0.05～0.5，本文设置为0.1。难点是参数λ2的调整，因参数λ2直接影响拉普拉斯噪声能量的大小，一般相对来说，λ2越大拉普拉斯噪声能量越小。本文只给出了参数λ2的经验调整范围，当目标遭受较大的噪声污染时，如完全遮挡，此时λ2通常取较小的值一般在0.000 5～0.01之间，反之参数λ2取值在0.01～0.5之间。

图9 几种追踪算法在快速运动和姿势旋转视频中的追踪效果

5 结 束 语

本文提出了同时稀疏表示的自适应追踪算法，该方法考虑了拉普拉斯噪声的影响，并根据噪声的能量大小自适应的选择稀疏模型。另外，模型使用了2种稀疏表示：同时稀疏(Lp,q)法，综合考虑了粒子之间的关系，使用ADMM方法对模型进行求解；对Lp模型，认为粒子之间的影响是相互独立的，可以分别通过LASSO算法分别求解；不同情境下的大量实验表明，这两种方法均得到了稳定的结果。

[1]LI A, LIN M, WU Y, et al. NUS-PRO： a new visual tracking challenge[J]. IEEE Transactions on Pattern Analysis &Machine Intelligence, 2016, 38(2)： 335-349.

[2]YANG H, SHAO L, ZHENG F, et al. Recent advances and trends in visual tracking： a review[J]. Neurocomputing, 2011,74(18)： 3823-3831.

[3]ADAM A, RIVLIN E, SHIMSHONI I. Robust fragments-based tracking using the integral histogram[J].IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 2006, 1： 798-805.

[4]ROSS D A, LIM J, LIN R S, et al. Incremental learning for robust visual tracking[J]. International Journal of Computer Vision, 2008, 77(1-3)： 125-141.

[5]LIWICKI S, ZAFEIRIOU S, TZIMIROPOULOS G, et al.Efficient online subspace learning with an indefinite kernel for visual tracking and recognition[J]. IEEE Transactions on Neural Networks and Learning Systems, 2012, 23(10)：1624-1636.

[6]BABENKO B, YANG M H, BELONGIE S. Robust object tracking with online multiple instance learning[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,2011, 33(8)： 1619-1632.

[7]YANG F, LU H, YANG M H. Robust superpixel tracking[J].IEEE Transactions on Image Processing, 2014, 23(4)：1639-1651.

[8]HENRIQUES J F, CASEIRO R, MARTINS P, et al.Exploiting the circulant structure of tracking by detection with kernels[C]//Computer Vision-ECCV. [S.l.]： Springer,2012, 7575： 702-715.

[9]WRIGHT J, YANG A Y, GANESH A, et al. Robust face recognition via sparse representation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2009, 31(2)：210-227.

[10]MEI X, LING H. Robust visual tracking and vehicle classification via sparse representation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,2011, 33(11)： 2259-2272.

[11]SUN B, LIU Z, SUN Y, et al. Multiple objects tracking and identification based on sparse representation in surveillance video[C]//IEEE International Conference on Multimedia Big Data. Beijing： IEEE Computer Society, 2015.

[12]WANG D, LU H, BO C. Online visual tracking via two view sparse representation[J]. IEEE Signal Processing Letters, 2014, 21(9)： 1031-1034.

[13]LI Y, HE Z, YI S, et al. The robust patches-based tracking method via sparse representation[C]//International Conference on Security, Pattern Analysis, and Cybernetics.Wuhan： IEEE, 2014.

[14]DUAN X, LIU J, TANG X. Visual tracking via weighted sparse representation[C]//International Conference on Intelligent Computing and Internet of Things. Harbin：IEEE, 2015.

[15]BAO C, WU Y, LING H, et al. Real time robust L1 tracker using accelerated proximal gradient approach[C]//IEEE Conference on Computer Vision and Pattern Recognition.Providence： IEEE, 2012.

[16]LU X, YAO H, SUN X, et al. Real-time visual tracking using L2 norm regularization based collaborative representation[C]//IEEE International Conference on Image Processing. Melbourne： IEEE, 2013.

[17]AHUJA N. Robust visual tracking via multi-task sparse learning[C]//Computer Vision and Pattern Recognition.Providence： IEEE, 2012.

[18]YAN Q, LI L, WANG C, et al. Kernel sparse representation for object tracking[C]//International Conference on Multimedia Information Networking and Security. Beijing：IET, 2013.

[19]WANG L, YAN H, LV K, et al. Visual tracking via kernel sparse representation with multikernel fusion[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2014, 24(7)： 1132-1141.

[20]WU Y, LIM J, YANG M H. Online object tracking： a benchmark[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Portland： IEEE,2013.

[21]ZHONG W, LU H, YANG M H. Robust object tracking via sparse collaborative appearance model[J]. IEEE Transactions on Image Processing, 2014, 23(5)： 2356- 2368.

[22]MEI X, LING H. Robust visual tracking using L1minimization[C]//IEEE 12th International Conference on Computer Vision. Kyoto： DBLP, 2009.

[23]WANG D, LU H, YANG M H. Online object tracking with sparse prototypes[J]. IEEE Transactions on Image Processing, 2013, 22(1)： 314-325.

[24]MAIRAL J, BACH F, PONCE J, et al. Online dictionary learning for sparse coding[C]//International Conference on Machine Learning. Quebec： DBLP, 2009.

[25]LEARNEDMILLER E, SEVILLALARA L. Distribution fields for tracking[C]//Computer Vision and Pattern Recognition. Providence： IEEE, 2012.

[26]HE J, ZHANG D, BALZANO L, et al. Iterative Grassmannian optimization for robust image alignment[J].Image and Vision Computing, 2014, 32(10)： 800-813.