带有Dzyaloshinski-Mariya相互作用的两比特纠缠量子Otto热机和量子Stirling热机∗

赵丽梅 张国锋

(北京航空航天大学物理科学与核能工程学院,北京 100191)(2017年5月24日收到;2017年8月22日收到修改稿)

1 引 言

随着量子信息科学的蓬勃发展,量子力学和热力学的交叉领域逐渐引起了越来越多物理学家的关注[1,2].自从量子热力学这一概念被Kieu首次提出以来,物理学者们在这一领域做了大量的研究工作,使得量子热力学循环性能成为近年来研究的热点[3,4].目前研究比较多的体系有自旋系统[5−27]、谐振子系统[28−31]二能级或多能级系统[32,33]以及腔量子电动力学系统[34,35]等.

Dzyaloshinski-Mariya(DM)相互作用[36,37]是一种具有反对称的各向异性超交换相互作用,可用来解释反铁磁材料中的弱铁磁性以及其他的新奇性质[38].近年来,人们也广泛讨论和研究了在各向异性交换作用下的海森伯模型,发现DM相互作用会对研究系统的性质产生重要的影响.例如,Zhang[39]探讨了具有DM相互作用的两个自旋各向异性系统纠缠量子热机.Wang等[40]研究了具有DM相互作用的各向异性海森伯XXZ模型的热纠缠等,这些研究工作都取得了丰富的成果.但是到目前为止,尚未见具体的DM相互作用对量子热机影响的探究.

为了进一步丰富量子热力学循环理论,本文以带有DM相互作用的两比特模型作为工作物质,构建一个四能级纠缠量子Otto热机和量子Stirling热机,通过保持其他参数不变,仅改变DM相互作用参数来研究DM相互作用对量子热机的影响.而这种操作在具体的实际过程中也很容易实现[41,42],例如,Niu等[43]研究了当保持外磁场不变,只有粒子间的自旋耦合系数J发生变化的四能级量子Otto热机.

通过数值计算,探究了循环过程中在不同的DM相互作用参数下对热机的基本热力学参数的影响,并且利用等值线图描绘和分析了纠缠与热量、功和机械效率之间的关系.

2 具有DM相互作用的量子Otto热机模型

量子Otto热机是以具有DM相互作用各向异性的两比特海森伯模型为工作物质,其哈密顿量可写为

式中J表示自旋耦合系数,反铁磁性物质对应J＞0,铁磁性物质对应J＜0,为了计算方便,本文只取J＞0;B是沿Z方向的连续外磁场;D表示DM相互作用矢量,σi(i=1,2)是泡利算符.为了简便,我们只考虑D=Dz时的情况,此时的哈密顿量可化简为

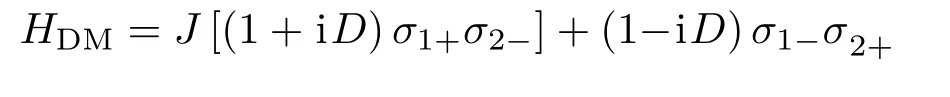
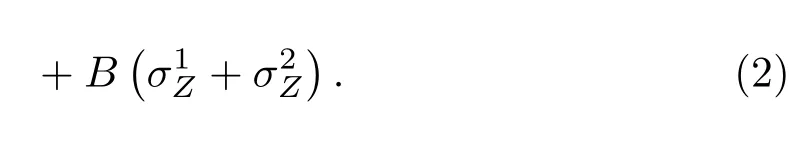
选|00〉,|11〉,|10〉,|01〉为基矢,则HDM的本征态为

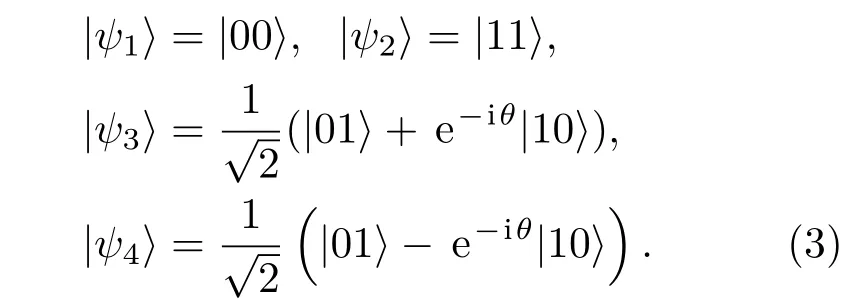
其中θ=arctanD,相应的四个本征值为

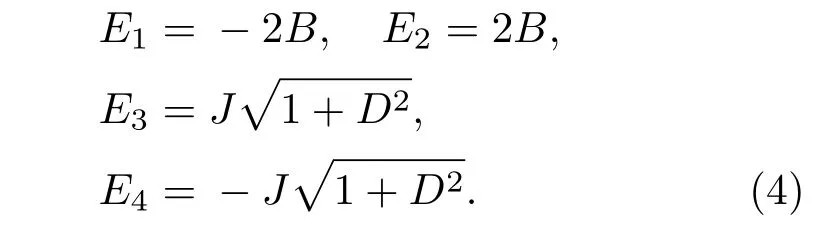
当系统处于热平衡态时,其状态密度算符可写为ρ=∑ipi|ψi〉〈ψi|. 其中,pi=exp(−βEi)/Z,配分函数Z=Tr[exp(−βEi)],β=1/(kBT).

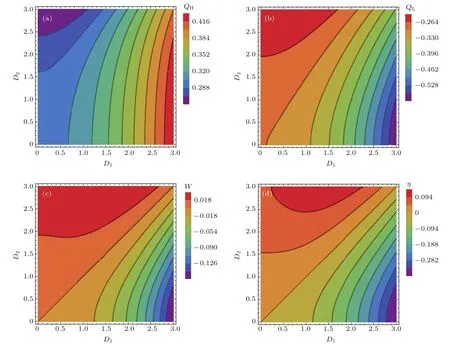
图1 (网刊彩色)当 T1=2,T2=1,J=1和B=4时,(a)QH,(b)QL,(c)W 和(d)η随D1和D2变化的等值线图Fig.1.(color online)Variations of heat transferred(a)QH,(b)QL,(c)net work input W and(d)the efficiency η of the QHE with variables D1and D2in isoline map for parameters T1=2,T2=1,J=1 and B=4.

量子Otto热机循环由两个量子等容过程和两个量子绝热过程构成,下面是量子Otto热机循环的四个阶段.

阶段一:初始时,体系的四个本征态的概率为pi,DM耦合相互作用为D=D1,外部磁场B保持不变,将体系与温度为TH的高温热源接触,经过一段时间,达到热力学平衡,在这个过程中系统本征能量Ei保持不变,体系的四个本征态的概率变为.在这个阶段中,只有热量的交换,不做功.

阶段二:移除热源,体系经历一个量子绝热过程,DM耦合作用从D1变到D2,这个过程要足够缓慢,使得每个量子态的概率不变,依旧为,体系各本征能级Ei变为.因此在这个过程中,只有做功而无热量的传递,指出要使该过程保持绝热,耦合作用的变化需要满足传统的量子绝热定理[16].

阶段三:与第一阶段相似,体系与温度为TL的低温热源持续接触,经过一段时间的耦合作用后达到热平衡状态,工作物质的每个态的占有概率由变为pi,体系各本征能级保持不变.在此过程中,由于占有概率的改变使体系与热源之间存在热传递,没有做功.

图2 (网刊彩色)当T1=2,T2=1,J=1和B=6时,(a)QH,(b)QL,(c)W 和(d)η随D1和D2变化的等值线图Fig.2.(color online)Variations of heat transferred(a)QH,(b)QL,(c)net work input W and(d)the efficiency η of the QHE with variables D1and D2in isoline map for parameters T1=2,T2=1,J=1 and B=6.

阶段四:与第二阶段类似,移除热源,体系再次经历量子绝热过程,这一过程,DM耦合作用从D2变到D1,每个本征态的占有概率pi均保持不变,体系各本征能级由又回到了Ei.此过程中体系只做功,没有热量的交换.

根据上述过程,可以得到在阶段一和阶段三的两个等容过程中,转移的能量分别为

式中,QH＞0和QL＜0分别代表系统吸热和放热.因此整个循环的输出功为

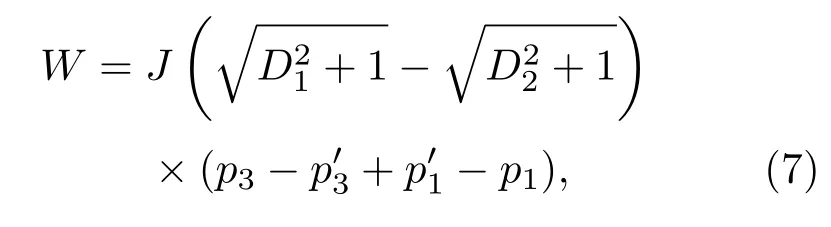
量子热机的机械效率为

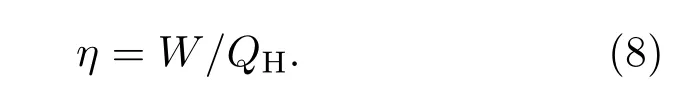
当T1=2,T2=1,J=1,磁场B分别为4和6时,我们给出了以D1,D2为变量的函数,通过数值分析,绘出了基本热力学量QH,QL,W,η随D1,D2变化的等值线图(如图1和图2所示).

从图1和图2可以得到4个结论:1)DM相互作用不仅能够提高系统的热纠缠度,而且会对Otto热机的基本量子热力学量产生很大的影响,既能影响工作热力学量的大小,也能影响其变化趋势;2)当系统做正功时,满足条件D1＜D2,这个结论也可以从(7)式中推理得到,当W＞0,有化简后得到B/T1＜B/T2;3)当W＞0时,QH＞−QL＞0始终成立,且在不同的外磁场参数下该纠缠热机机械效率都小于卡诺热机的效率,因此热力学第二定律始终成立;4)随着外磁场B的增大,做功和效率的取值范围也会越来越大.

3 具有DM相互作用的量子Stirling热机

在本节中,考虑了同样的耦合系统作为工作物质构建了量子Stirling循环.量子Stirling循环是经典Stirling循环的量子推广,包括两个量子等温过程和两个量子等容过程[44].该热机的四个过程可以做如下表述.

阶段一:是量子等温过程.在该过程中,系统与处于TH的高温热源接触.DM耦合作用缓慢的从D1变到D2,外部磁场B保持不变,并且在此过程中,系统与热源在任何一个时刻都保持热平衡.系统从高温热源吸热为Q1.

阶段二:是量子等容过程.在该过程中,DM耦合作用为D2保持不变,系统的温度从TH减小到TL,该过程系统不对外做功,但释放热量为Q23.

阶段三:是另外一个量子等温过程.在该过程中,系统与温度为TL的低温热源接触,DM耦合作用从D2变到D1.系统的温度保持不变.系统向低温热源释放热量(记为Q2).

阶段四:是另一个量子等容过程.在该过程中,DM耦合作用为D1保持不变,系统吸收热量(记为Q41),但不对外做功.整个系统循环过程如图3所示.

图3 (网刊彩色)量子Stirling热机的D-U(DM作用:内能)Fig.3.(color online)Scheme illustration of a quantum Stirling heat engine cycle based on DM interaction-energy D-U diagram.

在两个等容过程中,由于系统对外不做功,因此其热传递等于内能U的改变.则该系统内能

从(9)式可以得到系统与回热器之间的热交换Q23和Q41分别为

两个等温过程中,系统与外界环境之间的热交换为dQ=TdS,这里的S是工作物质的熵.则该系统熵为

代入到dQ=TdS中,得到在两个等温过程中系统从高温热源吸收的热量以及向低温热源释放的热量Q1和Q2分别为

与量子Otto循环很不相同,量子Stirling循环可以使用回热器.通过回热器便可以使循环过程中的阶段二释放的热量会在阶段四中重新被系统吸收,从而达到改善热机循环的性能的目的.典理想气体为工作物质的循环而言,系统达到最佳回热的条件是Q23+Q41=0.然而,以量子系统为工作物质的循环却并非如此.事实上,对于量子循环而言,系统与回热器在两个等容过程中的净热传递量需要满足:ΔQ=Q23+Q41,因此系统在整个循环过程中,从高温热源(温度为T1)吸收的热量和从低温热源(温度为T2)释放的热量为

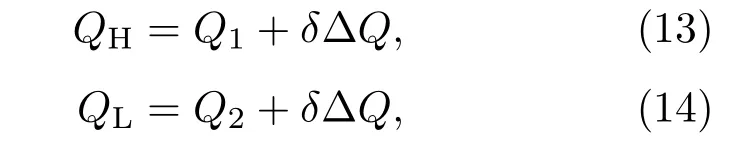
(13)式中,如果ΔQ＜0,δ=0;ΔQ＞0,δ=1;(14)式中,如果ΔQ＞0,δ=0;ΔQ＜0,δ=1.以这些热交换为基础,根据热力学第一定律可以得出系统对外做功为

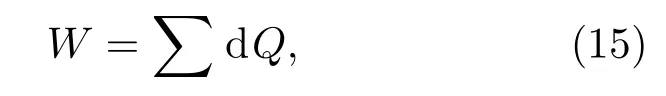
W＞0代表系统对外界做功.量子热机的机械效率为

令T1=2,T2=1,J=1,B=4,通过数值软件,就可以绘制出量子Stirling热机在整个循环过程中ΔQ不同情况下的基本热力学量QH,QL,W,η随D1,D2的变化的等值线图,结果如图4–图6所示.

从所示的等值线图中可以得出3个结论:1)DM相互作用会对量子Stirling循环热机的基本量子热力学产生重要影响;2)当W＞0时,QH＞−QL＞0,满足条件D1＜D2,这个结论也可以从(14)式中推理得到,最终化简后得到B/T1＜B/T2;3)在量子Stirling热机循环中,热机由于回热器的使用,其循环效率甚至会超过Carnot效率,热力学第二定律在整个循环中都始终成立.

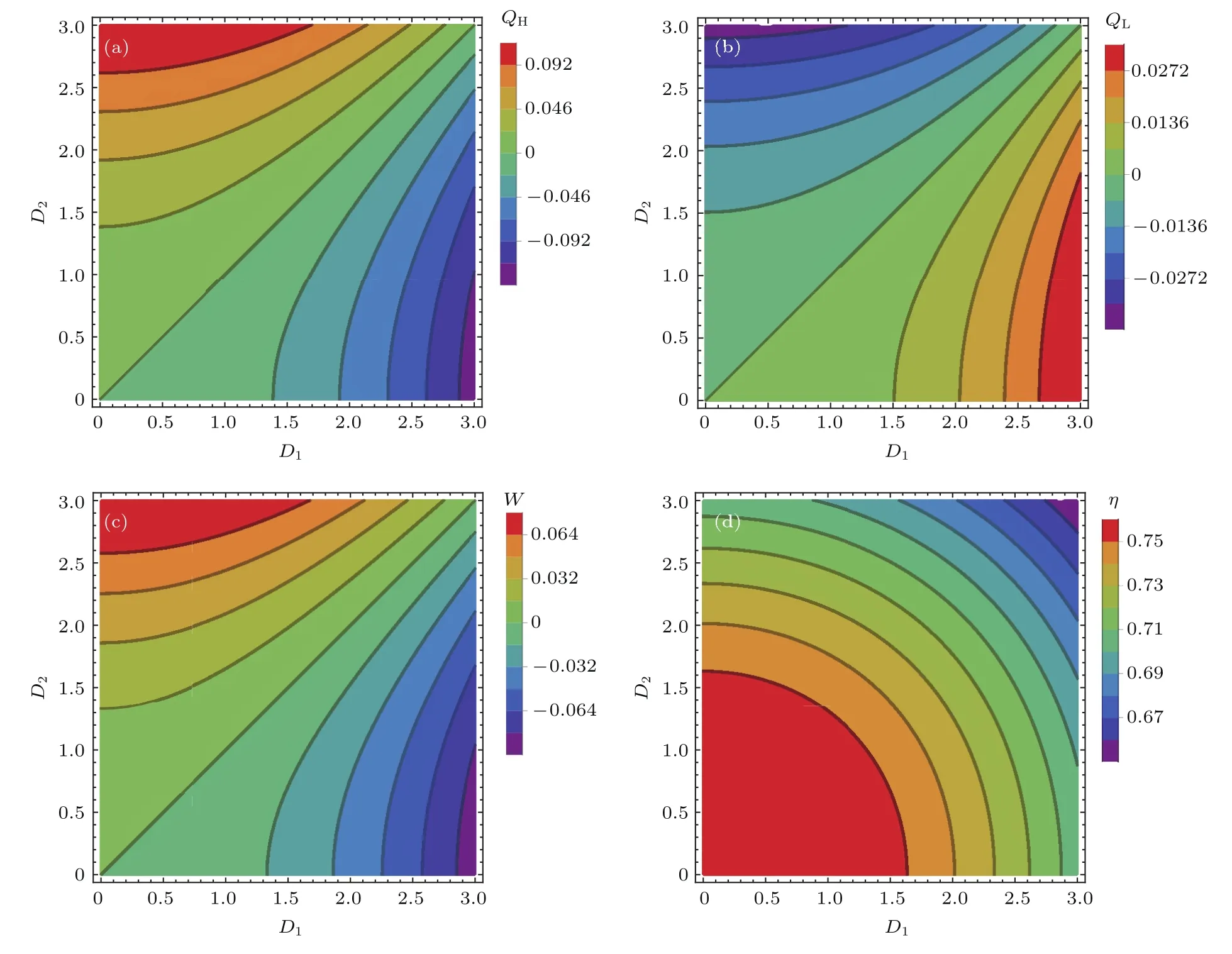
图4 (网刊彩色)在Q23+Q41＞0情况下,T1=2,T2=1,J=1和 B=4时,(a)QH,(b)QL,(c)W 和 (d)η随D1和D2变化的等值线图Fig.4.(color online)In the case of Q23+Q41＞0,variations of heat transferred(a)QH,(b)QL,(c)net work input W and(d)the efficiency η of the QHE with variables D1and D2in isoline map for parameters T1=2,T2=1,J=1 and B=4.

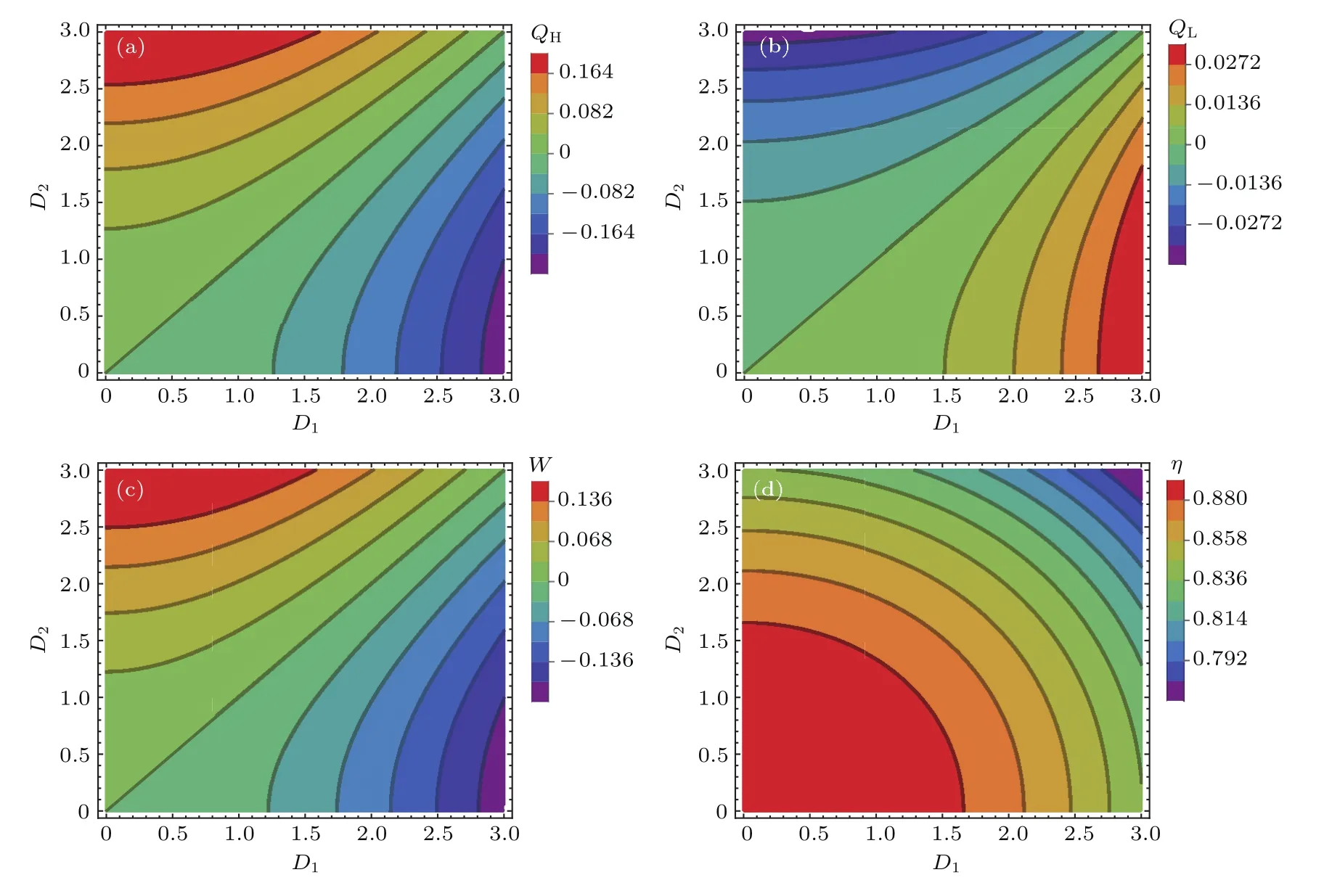
图5 (网刊彩色)在Q23+Q41=0情况下,T1=2,T2=1,J=1和B=4时,(a)QH,(b)QL,(c)W 和 (d)η随D1和D2变化的等值线图Fig.5.(color online)In the case of Q23+Q41=0,variations of heat transferred(a)QH,(b)QL,(c)net work input W and(d)the efficiency η of the QHE with variables D1and D2in isoline map for parameters T1=2,T2=1,J=1 and B=4.

4 结 论

以含有DM相互作用的两比特模型为工作物质构建了一个纠缠量子热机.分别介绍了两种不同的量子热机模型:量子Otto热机和量子Stirling热机.通过保持其他参量不变,只有DM相互作用发生改变,利用数值运算,分析出了热机循环中DM相互作用与热传递、做功以及效率等热力学量之间的关系.结果表明:DM相互作用对两种热机的基本热力学量都会产生重要影响;发现量子Otto热机的机械效率始终小于卡诺热机的效率,但是量子Stirling热机的循环效率大于量子Otto热机,甚至可以超过Carnot效率.在这两个纠缠体系中,热力学第二定律都依然成立.

[1]Scovil H E D,Schulz-Dubois E O 1959Phys.Rev.Lett.2 262

[2]Geusic J E,Schulz-Dubois E O,Scovil H E D 1967Phys.Rev.156 343

[3]Kieu T D 2004Phys.Rev.Lett.93 140403

[4]Kieu T D 2006Eur.Phys.J.D39 115

[5]Altintas F,Hardal A U C,Mustecaplioglu O E 2015Phys.Rev.A91 023816

[6]Wang X G 2001Phys.Rev.A64 012313

[7]Thomas G,Johal R S 2011Phys.Rev.E83 031135

[8]Huang X L,Wang L C,Yi X X 2013Phys.Rev.E87 012144

[9]Zhou Y,Zhang G F,Li S S 2009Europhys.Lett.86 50004

[10]Zhang G F 2007Phys.Rev.A75 034304

[11]Feldmann T,KosloffR 2004Phys.Rev.E70 046110

[12]Feldmann T,KosloffR 2003Phys.Rev.E68 016101

[13]KosloffR,Feldmann T 2002Phys.Rev.E65 055102

[14]Henrich M J,Mahler G,Michel M 2007Phys.Rev.E75 051118

[15]Zhang T,Liu W T,Chen P X,Li Z 2007Phys.Rev.A75 062102

[16]Thomas G,Johal R S 2014Eur.Phys.J.B87 166

[17]Huang X L,Wang T,Yi X X 2012Phys.Rev.E86 051105

[18]Huang X L,Liu Y,Wang Z,Niu X Y 2014Eur.Phys.J.Plus129 4

[19]Wu F,Chen L,Sun F,Wu C,Li Q 2006Phys.Rev.E73 016103

[20]Ivanchenko E A 2015Phys.Rev.E92 032124

[21]Altintas F,Müstecaplioğlu Ö E 2015Phys.Rev.E92 022142

[22]He X,He J,Zheng J 2012Physica A391 6594

[23]Cakmak S,Altintas F,Müstecaplioğlu Ö E 2016Eur.Phys.J.Plus131 197

[24]Wang H,Liu S,He J 2009Phys.Rev.E79 041113

[25]Hubner W,Lefkidis G,Dong C D,Chaudhuri D 2014Phys.Rev.B90 024401

[26]Azimi M,Chotorlishvili L,Mishra S K,Vekua T,Hubner W,Berakdar J 2014New J.Phys.16 063018

[27]Albayrak E 2013Int.J.Quantum.Inform.11 1350021

[28]Dillenschneider R,Lutz E 2009Europhys.Lett.88 50003

[29]Woo C H,Wen H,Semenov A A,Dudarev S L,Ma P W 2015Phys.Rev.B91 104306

[30]Roßnagel J,Abah O,Schmidt-Kaler F,Singer K,Lutz E 2014Phys.Rev.Lett.112 030602

[31]Zhang X Y,Huang X L,Yi X X 2014J.Phys.A:Math.Theor.47 455002.

[32]Wang R,Wang J,He J,Ma Y 2013Phys.Rev.E87 042119

[33]Uzdin R,KosloffR 2014Europhys.Lett.108 40001

[34]Altintas F,Hardal A U C,Mustecaplioglu O E 2015Phys.Rev.A91 023816

[35]Quan H T,Zhang P,Sun C P 2006Phys.Rev.E73 036122

[36]Dzyaloshinskii I 1958J.Phys.Chem.Sol.4 241

[37]Moriya T 1960Phys.Rev.Lett.4 228

[38]Sun Q F,Xie X C,Wang J 2007Phys.Rev.Lett.98 196801

[39]Zhang G F 2008Eur.Phys.J.D49 123

[40]Li D C,Wang X P,Cao Z L 2008J.Phys.Condens.Matter20 325229

[41]Zhong X M,Nguyen B A,Yun J X 2016Phys.Rev.E94 042135

[42]RoSSnagel J,Dawkins S T,Tolazzi K N 2016Science352 325

[43]Niu X Y,Huang X L,Shang Y F,Wang X Y 2015Int.J.Mod.Phys.B29 1550086

[44]Huang X L,Niu X Y,Xiu X M,Yi X X 2014Eur.Phys.J.D68 32