小世界神经元网络随机共振现象:混合突触和部分时滞的影响∗

李国芳 孙晓娟

(北京邮电大学理学院数学系,北京 100876)

(2017年7月18日收到;2017年8月29日收到修改稿)

1 引 言

神经系统中噪声诱导的随机共振行为是神经元进行信息传递的重要机制,近年来受到国内外学者的广泛关注,特别是在大脑神经系统中也观察到随机共振现象[1,2].随机共振是指非线性系统在弱噪声和外界弱周期信号的共同作用下,系统输出信号的功率谱在周期信号对应的频率处出现一个峰值[3,4].而相干共振是随机共振的衍生概念,又称随机自共振,它是指在没有外界信号的激励、只有噪声的作用下系统的输出响应在某一噪声强度下也能达到最大值[5].大量研究显示噪声能够使神经元对弱信号的处理能力加强,使信息在神经元间有效传递[6,7].Sun等[8,9]通过对Hodgkin-Huxley神经元网络施加高斯噪声和非高斯色噪声发现中等的噪声强度使网络空间相干共振最佳.近年来,关于共振行为的研究取得了很大进展.Zhou等[10]研究了一列耦合的Fitz Hugh-Nagumo神经元,发现耦合能够增强噪声诱导的相干共振.进一步,一些学者在小世界神经元网络中发现适中强度的噪声和适当数目的加边能增强噪声诱导的相干多共振[9,11−14].Liu等[15]在具有格子耦合的二维神经元网络中发现噪声能诱导神经元网络产生螺旋波,即产生空间相干多共振.近些年,相对于经典的噪声诱导的随机共振,异质性诱导共振也引起了广泛关注[16,17].此外,Perc[18]首次通过把阈下信号起搏器加入网络中一个兴奋神经元上发现适中的耦合强度也可以促进小世界网络的随机共振.

神经元间有两种基本的突触耦合,即电耦合和化学耦合;而每一种突触又具有两种耦合方式,兴奋性耦合和抑制性耦合[19,20].在以往的研究中,兴奋电突触耦合和化学突触耦合已经在各种现象中得到广泛研究.例如,Shi等[21]分别在电耦合和化学耦合下研究了Hindmarsh-Rose神经元模型的同步行为;Wang等[22]在兴奋性电突触耦合网络里研究了异质性神经元和时滞对随机共振的影响.事实上,电和化学两种突触耦合在神经元间是可以同时存在的[23,24].例如,Kopell和Ermentrout[25]发现电突触和化学突触对神经元网络的完全同步具有相互补充的作用.Yilmaz等[26]在带有混合突触的无标度网络中发现电突触比化学突触更能有效地促进阈下信号对系统的响应程度;Yu等[27]进一步在混合突触和时滞作用下的小世界网络中发现,在低噪声情况下通过引入电突触耦合能有效提高弱信号的探测和传播.最近,理论和临床研究表明大脑中兴奋性突触和抑制性突触会维持恰当比例以确保身体的自我平衡(E-I平衡)以及实现信息的有效传递[28−32];而当这种比例失调时会引起多种神经性疾病,如抑郁症、精神分裂症、癫痫病等[33].因此,目前关于兴奋抑制突触平衡机制的调节及E-I反常行为被广泛研究[34−36].

另外,由于信号在轴突传播时有限的传播速度,以及在轴突和突触间隙传递时的时间流失会产生时滞[37].因此,信息传递时滞对神经元网络的随机共振有很重要的影响.值得注意的是,之前的研究考虑的是耦合神经元间都有时滞的情况.如Wang等[38]在无标度网络中发现当时滞为阈下信号周期的整数倍附近,时滞可诱导网络产生随多共振行为.Yu等[27,39]在带有电和化学混合突触的小世界网络和模块网络中发现时滞可以提高或抑制小世界网络的随机共振和同步行为,且电突触和化学突触对时滞诱导的共振和同步起相互补充作用.但是,在实际神经元系统中,一些神经元间的信息传递是瞬时的或时滞是可以忽略的,那么部分时滞会对网络的随机共振有什么影响呢？Sun等[40−42]分别探讨了部分时滞对电耦合和化学耦合随机多共振和同步转迁的影响,发现随网络中时滞边比例改变,部分时滞使随机多共振和同步转迁发生显著变化.

在此基础上,本文拓宽范围,进一步研究部分时滞对带有混合突触比例的小世界网络的随机共振行为的影响.第2部分中主要介绍模型和网络设置.首先,用二维Rulkov映射神经元模型刻画网络中节点的局部动力学,然后在其基础上加入高斯白噪声,混合耦合电流和部分时滞构成神经元网络模型;接着,构建了具有带有电兴奋、电抑制、化学兴奋、化学抑制混合突触耦合的小世界神经元网络,并且给出随机共振的度量指标.第3部分先在无时滞情况下讨论了噪声强度、化学突触比例和兴奋性突触比例三者间的关系,并且给出了机理解释;然后在固定的混合突触比例下,研究部分时滞和噪声对混合网络随机多共振的影响.最后,第4部分给出了总结和讨论.

2 构建系统模型和混合网络

2.1 系统模型和分析方法

二维Rulkov映射模型[43]具有低维、离散等特点,并且能够模拟复杂的非线性神经元系统的动力学行为特征,本文以它作为神经元网络的节点动力学模型.其方程如下所述:

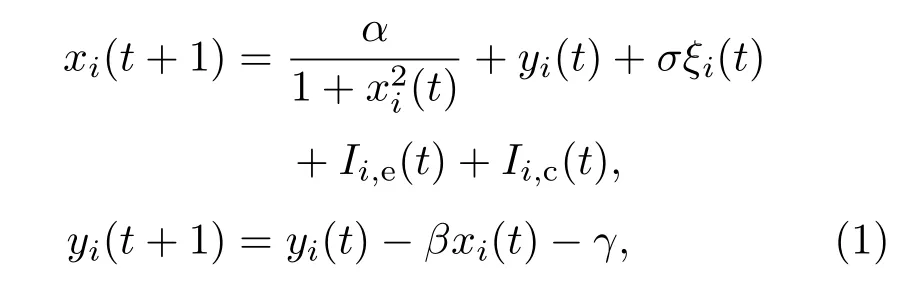
其中,下标i表示第i个神经元,x表示神经元膜电位,y是恢复变量;t代表离散的时间变量.这里设定膜电位xi(t)从下到上穿过阈值0时为放电时刻.β和γ是模型参数,固定β=γ=0.001.当β和γ固定后,参数α决定神经元的动力学行为.设定α=2.3,使单个神经元产生周期峰放电,如图1所示,神经元固有振荡周期T=820.ξi(t)是高斯白噪声,满足〈ξi(t)〉=0,〈ξi(t1)ξj(t2)〉=δijδt1t2. 如果i=j(t1=t2), 则δij=1(δt1t2=1); 否则,δij=0(δt1t2=0).σ表示噪声强度.

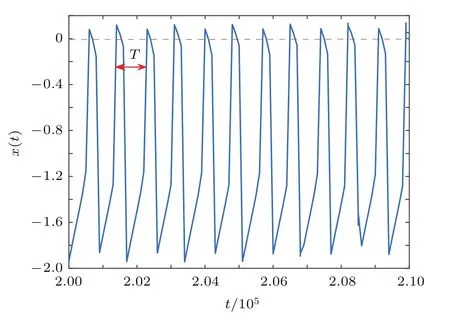
图1 单个Rulkov神经元放电序列图(α=2.3)Fig.1.Firing trains for an isolated Rulkov map neuron when α=2.3.

此外,Ii,e(t)代表其他神经元流入第i个神经元的电突触电流总和,其具体表达式为

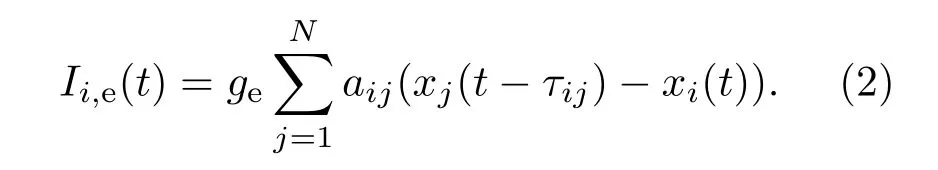
这里,ge表示神经元间电耦合强度,若ge=0.005为正数时,表示以兴奋电突触耦合;若ge=−0.005为负数时,则表示以电抑制突触耦合.(aij)N×N为电突触连接矩阵,当第i个神经元和第j个神经元通过电突触连接时,aij=aji=1;其他情况矩阵元素值都为0.此外,耦合项中τij表示第i个和第j个神经元之间信息传递的延迟时间,当第i个和第j个神经元之间连接且以概率pdelay产生时间延迟时,τij=τji=τ;当两神经元间的时间延迟很小可以忽略时,τij=τji=0.这里,pdelay表示网络所有连边中时滞边所占的比例.

同理,Ii,c(t)代表其他神经元流入第i个神经元的化学突触电流总和,其表达式为

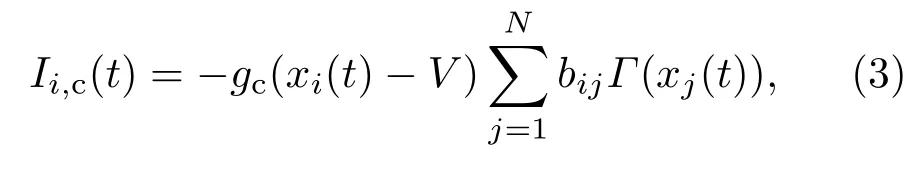
其中,gc表示化学突触耦合强度,设置gc=0.01;V是化学突触反转电压,当V=0.2时两个神经元通过兴奋性化学突触相连接,当V=−1.9时两个神经元通过抑制性化学突触相连接;(bij)N×N为化学突触耦合矩阵,若两个神经元通过化学突触相连接,则bij=bji=1;否则,其他情况矩阵元素值都为0.

化学突触耦合项中S型函数的定义如下:

这里,Θs=−1.0,λ=30代表突触前神经元影响突触后神经元的一个阈值.同样地,τij表示信息传递时滞,若两个神经元连接且以概率pdelay产生时间延迟时,τij=τji=τ;若两神经元间的时间延迟很小可以忽略时,τij=τji=0.

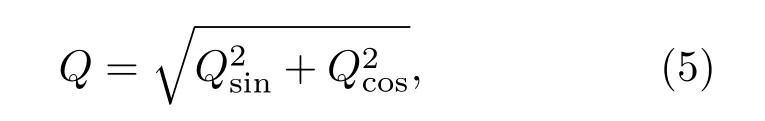
其中,

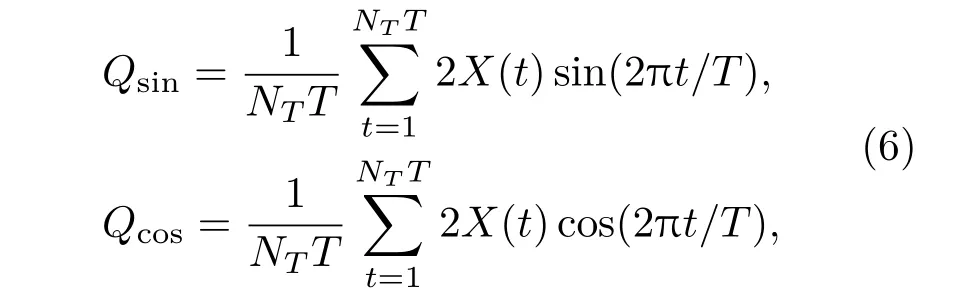
这里,NT为整数,表示振荡周期的个数;NTT为神经元膜电位时间序列的长度.Q值越大,输出信号和系统固有放电频率的相干性越大,即系统对信号的响应强度越大,网络产生的随机共振越好.在数值模拟时,取NT=300个周期记录xi(t),并且将最终结果平均20次.

2.2 混合突触网络构建

小世界网络由Watts和Strogatz提出[46],我们根据其算法选用N=200个神经元,每个神经元与它邻近的k=6个神经元环状相连构成规则网络.然后以重连概率p=0.1重新连接网络中的每一条边,并且保证两个顶点之间最多能连一次且本身不能自连和不能产生孤立节点.初始,控制网络神经元单纯以兴奋性电突触方式耦合,然后通过概率f逐渐将部分兴奋电突触连接转变成兴奋化学突触连接;紧接着,通过概率fb将网络从兴奋电突触和兴奋化学突触连接转变为带有电抑制和化学性抑制的混合突触连接网络.值得注意的是,在所有耦合连边中带有时滞τ的连边以概率pdelay随机存在.这样,具有电突触和化学突触两种不同突触类型,并且以兴奋和抑制两种不同方式随机连接,带有部分时滞的Watts-Strogatz小世界网络构建完成.这里,f表示网络中化学突触所占的比例,即

3 数值结果

3.1 噪声和混合突触对随机共振的影响

本部分主要考虑无时滞(τ=0)情况下混合突触比例fb,f和噪声强度σ对随机共振的影响.首先在固定fb=0.8,f=0.1时,观察不同噪声强度σ下混合小世界网络全体神经元的放电时空图,如图2所示.当网络没有噪声时σ=0(图2(a)),只有很少的神经元产生放电行为,且放电稀松.当σ=0.015(图2(b)),放电频率增加且网络整体放电行为显著增强.当噪声强度增大到σ=0.025(图2(c))时,网络呈现规则有序的放电.而当σ=0.045(图2(d))时,产生放电的神经元数量和放电频率再次减弱,放电有序性降低.当噪声强度继续增大到σ=0.06(图2(e))时,网络的时空图呈现混乱不规则放电状态.不难看出,噪声强度影响混合突触小世界网络的放电有序性,存在恰当的噪声强度使网络放电行为最佳,偏大或偏小的噪声强度减弱或抑制神经元的放电行为.

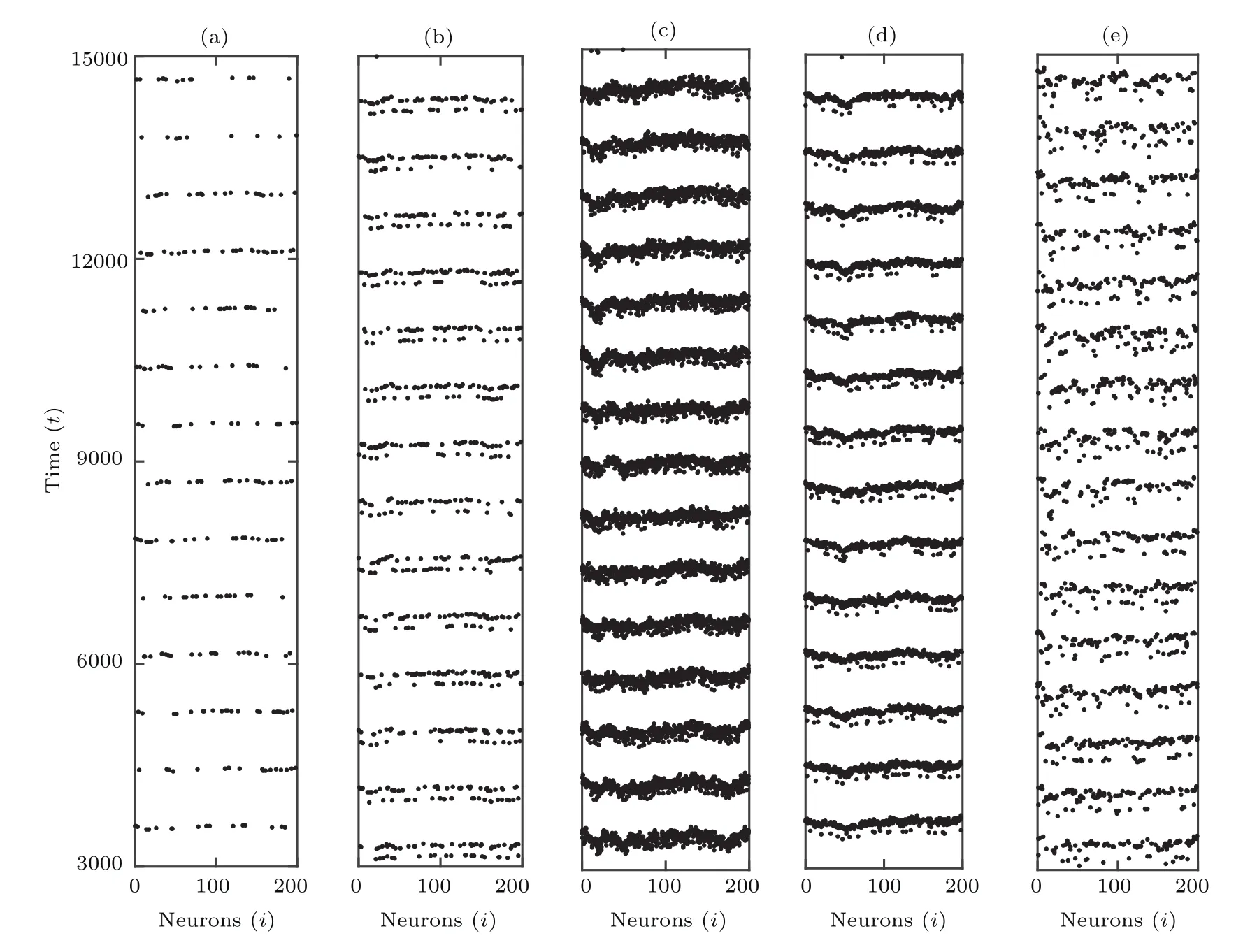
图2 不同噪声强度σ下,小世界网络中全体神经元的放电时空序列图 (a)σ=0;(b)σ=0.015;(c)σ=0.025;(d)σ=0.045;(e)σ=0.06;其他参数为fb=0.8,f=0.1,τ=0;这里,膜电位xi(t)从下到上穿过阈值0时为放电时刻Fig.2.Spatiotemporal patterns for different values of σ for τ=0:(a) σ =0;(b) σ =0.015;(c) σ =0.025;(d) σ =0.045;(e)σ=0.06.Other parameters are fb=0.8,f=0.1.

图3展示了响应强度Q随噪声强度σ变化的趋势.由图3可知,随σ的变化,系统响应强度Q值先增大后减小,且当σ=0.025时Q值最大.从而说明在fb=0.8,f=0.1时混合突触网络存在恰当的噪声强度σ=0.025使系统响应Q达到最佳,即产生随机共振现象;而偏大或偏小的噪声强度都会使随机共振减弱.

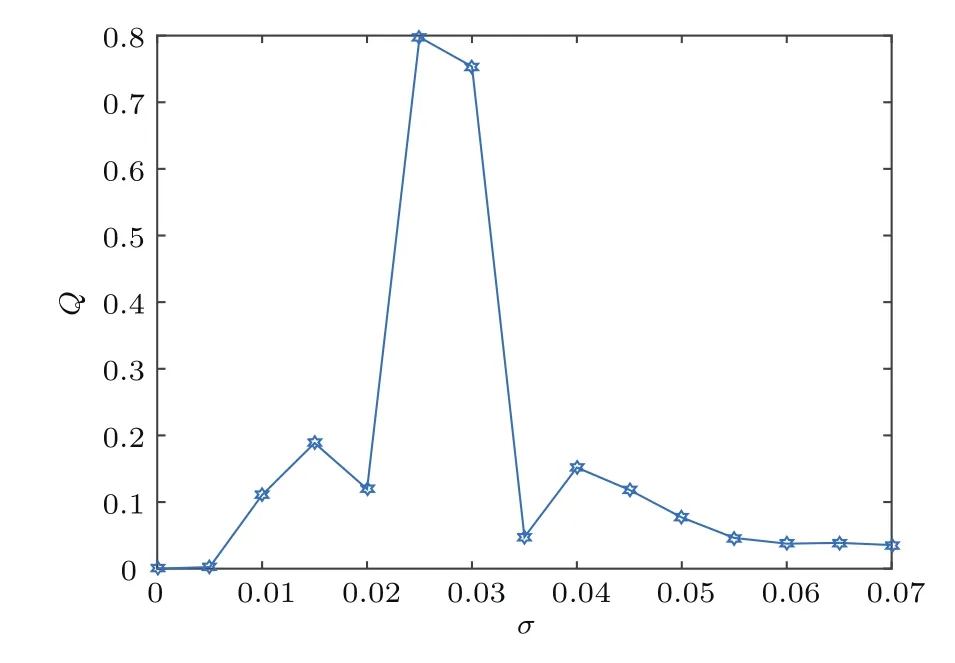
图3 响应强度Q随噪声强度σ的变化(fb=0.8,f=0.1,τ=0)Fig.3.Dependence of response amplitude Q with respect to noise intensity σ for τ =0.Other parameters are fb=0.8,f=0.1.

图4 不同化学突触比例f下,响应强度Q随噪声强度σ和抑制性突触比例fb变化的等高线图 (a)f=0.1;(b)f=0.5;(c)f=0.9;其他参数为τ=0Fig.4.Dependence of response amplitude Q with respect to τ and fb with different f:(a)f=0.1;(b)f=0.5;(c)f=0.9.Other parameter is τ=0.

那么,当fb,f发生改变,最佳噪声强度σ会如何变化呢？为了定量研究三者之间的关系,分别在化学突触比例f=0.1,0.5,0.9,即网络以电耦合为主、化学耦合和电耦合均衡、化学耦合为主三种不同形式的混合突触网络下观察噪声强度σ和兴奋性突触比例fb对系统响应Q的影响.如图4所示,对于不同的f,当兴奋性突触比例fb超过某个阈值时,不同混合突触网络会对应不同的噪声取值区间,使系统响应Q达到最佳.如f=0.1(图4(a)),当fb＞0.3时,存在恰当的噪声取值区间0.02＜σ＜0.035,使系统响应强度Q达到最佳;而当fb＜0.4,噪声强度不能引导网络产生共振行为.同样地,当f=0.5(图4(b))时只有在兴奋性突触比例fb＞0.4时,存在较大的噪声取值区间0.04＜σ＜0.05,使系统响应强度Q达到最佳,即共振行为显著.而当混合突触网络以化学突触耦合为主时,即f=0.9(图4(c)),仅在0.7＜fb＜0.85时存在两个噪声区间0.03＜σ＜0.04和0.055＜σ＜0.065,使系统响应强度Q达到最佳,产生随机双共振.基于以上分析,不难看出当fb较小时,即混合突触网络主要以抑制性突触耦合为主时,不存在恰当的噪声强度使系统实现共振行为.而当fb较大即网络以兴奋性突触耦合为主时,存在确定的噪声取值区间,使系统响应最佳.比较图4(a)—(c)发现,当网络中化学突触比例f增大时,确保达到系统最佳响应Q所对应的噪声区间随之改变,并且呈增大趋势.有趣的是,当混合突触网络主要以化学突触耦合时(如图4(c)),只有在网络中兴奋性突触所占比例为0.7＜fb＜0.85(即兴奋性突触:抑制性突触≈4:1)时才存在恰当的噪声强度使系统响应Q达到最佳.而这一突触比例与最近的生物临床和理论结果相似[28],其中研究显示当兴奋和抑制突触维持恰当比例时信息能有效传递.综上,噪声主要对兴奋性突触耦合起明显作用;并且当f较大即混合突触网络以化学突触耦合为主时,仅当兴奋性突触和抑制性突触为恰当比例(0.7＜fb＜0.85)时,才存在最佳噪声强度使系统响应Q达到最好.

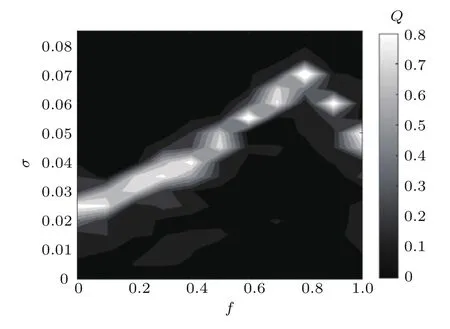
图5 响应强度Q随噪声强度σ和化学突触比例f变化的等高线图(其他参数为fb=0.8,τ=0)Fig.5.Dependence of response amplitude Q with respect to σ and f for fb=0.8 and τ=0.

基于以上现象,系统达到最佳响应的Q对应的噪声强度σ随化学突触比例f变化时会发生显著变化,那么变化趋势如何呢?特别地,由于在fb=0.8时不同f所对应的网络都能产生随机共振行为,因此固定fb=0.8,在二维平面σ-f内观察Q的变化趋势,结果如图5所示.从图5看出,随f增加,最佳噪声强度σ呈线性增长趋势.但是,当f＞0.8时,σ随f的增加开始非连续性递减;特别地,在一些f值时,会对应两个不同的噪声取值区间,使系统响应Q达到最佳,从而说明图4(c)中f=0.9时存在两个不同噪声取值区间系统出现双共振现象的原因.因此,可得出通常对于一个网络只对应一个特定范围的噪声取值区间使系统响应最佳的结论;但是,当混合突触网络中化学突触比例较大时,最佳噪声强度反而变小,并且存在两个噪声取值区间使系统出现双共振行为.除此之外,相同的噪声强度也可以使多个不同的混合突触网络实现共振行为.

综上所述,得出如下结论:1)网络中兴奋性突触比例fb影响随机共振的产生,即在以兴奋性突触为主的混合突触网络中(fb较大时),存在恰当的取值区间且系统能够产生共振行为;但在抑制性为主的混合突触网络(fb较小时)中,没有恰当的噪声使系统产生共振行为;2)最佳噪声强度σ主要受f的影响而发生变化,且通常σ随f呈线性增加关系.

下面进行机理分析.首先,为说明兴奋性突触比例fb影响随机共振产生的原因,这里取f=0.1(图4(a))进行阐述,其他情况类似.选取fb=0.2(抑制性突触为主的混合突触网络)和fb=0.8(兴奋性突触为主的混合突触网络)两种情况,分别观察耦合和噪声对神经元放电序列的影响,结果如图6所示.图6(a)显示fb=0.2只有耦合没有噪声的情况,可以看到由于网络以抑制性突触为主导,受抑制性耦合电流的作用膜电位显著降低,从而导致神经元不能产生较大幅值的放电;而当进一步给网络施加噪声后,如图6(c)所示,噪声使神经元放电幅值再次减弱,只能产生阈下振荡行为,因此导致网络全体神经元无法产生较强的放电,从而使系统响应Q值很小不能产生共振行为.而当fb=0.8时,没有噪声作用的情况如图6(b)所示,可以看出受兴奋性电流的作用,神经元依然保持周期有序性放电,且膜电位更显著;施加噪声后如图6(d),不同噪声强度下每个神经元依然呈现周期峰放电状态,只是在相同时间点上神经元的放电节律存在差异,这从时空图2也可看出.由此解释了适当的噪声强度下,较大的fb所对应的系统响应强度Q值较大,即网络能够产生随机共振行为的原因.需要说明的是,当f较大网络主要以化学突触耦合为主时(如图4(c)所示),尽管较大的fb下受兴奋性突触的作用每个神经元都呈现放电状态,但是由于化学突触主要靠神经递质传递信号,从而导致不同神经元间的信息传递在时间和作用上复杂性增强.因此仅当兴奋性突触所占比例恰当(约为0.7＜fb＜0.85)时,才存在噪声强度使全体神经元同步放电,系统响应Q值最大,从而产生随机共振行为.

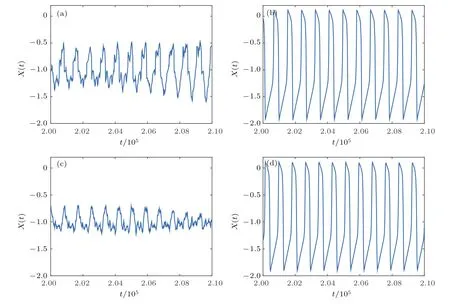
图6 受耦合和噪声影响的平均场X(t)放电序列图 (a)fb=0.2,σ=0;(b)fb=0.8,σ=0;(c)fb=0.2,σ=0.025;(d)fb=0.8,σ=0.025;其他参数为f=0.1,τ=0Fig.6.Different mean fi eld activity X(n)for different fb:(a)fb=0.2,σ =0;(b)fb=0.8,σ =0;(c)fb=0.2,σ=0.025;(d)fb=0.8,σ=0.025.Other parameters are f=0.1,τ=0.

其次解释最佳噪声强度σ随f的影响而发生变化的原因.首先定义平均峰峰间隔〈ISI〉[40],其形式如下:

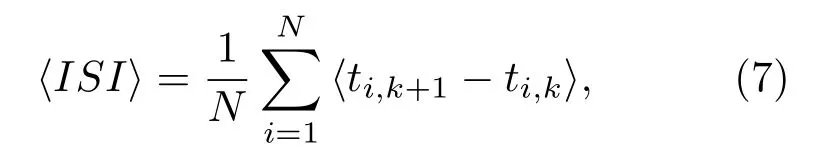
其中ti,k为第i个神经元的第k次放电时刻,〈·〉表示平均值.图7分别给出了在fb=0.8时,不同f所对应的所有神经元的平均放电间隔〈ISI〉随噪声强度σ变化的趋势图.由图7可知,当f变化时,〈ISI〉与系统固有周期T相等所对应的噪声强度发生变化,从而导致最佳响应Q对应的噪声强度发生改变.如f=0.1时仅当σ≈0.025,平均放电时间间隔〈ISI〉与系统固有放电周期T=820相等;同理f=0.5,当σ≈0.045时,平均放电时间间隔〈ISI〉与系统固有放电周期T=820相等;而当f=0.9时,对应两个噪声强度σ≈0.04和σ≈0.06,因此可在图4(c)中看到存在两个噪声区间使系统响应Q最佳.

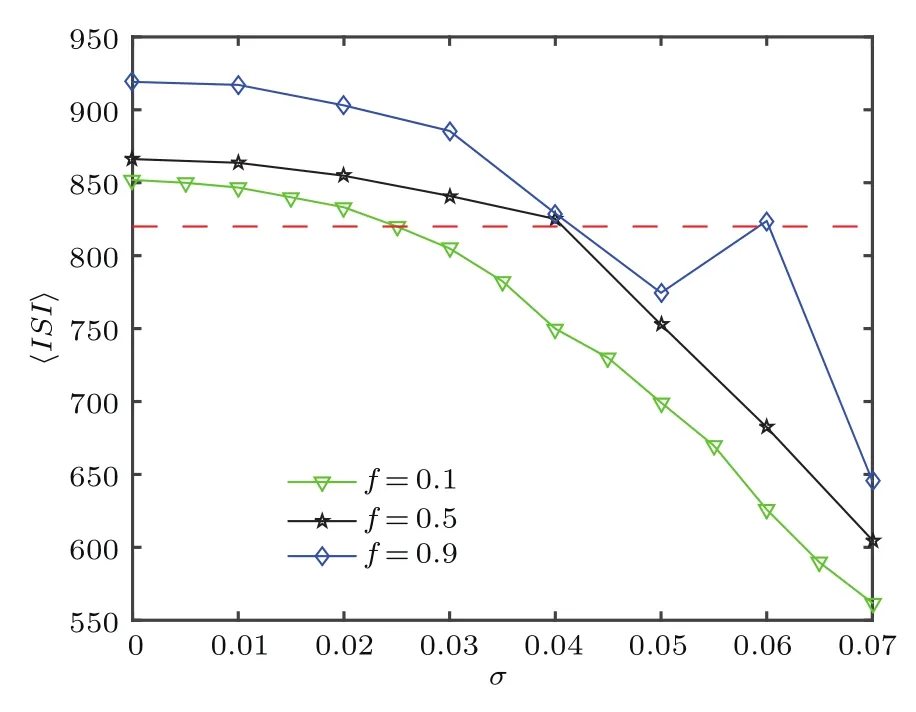
图7 (网刊彩色)不同f下,平均放电周期〈ISI〉随噪声强度σ的变化(其他参数为fb=0.8,τ=0)Fig.7.(color online)Dependence of mean fi ring period〈ISI〉with respect to noise strength σ for different f.Other parameters are fb=0.8,τ=0.

3.2 部分时滞对混合网络随机共振的影响

基于前面的研究,由于抑制性突触为主的混合突触网络中共振较弱并且当fb≈0.8时不同f对应的网络共振最佳,所以下面统一设置fb=0.8,即在兴奋性突触为主的混合突触网络中研究部分时滞对随机共振的影响.图8展示了不同pdelay下,网络响应强度Q随τ变化的趋势图.当pdelay=0.1时,系统响应强度Q随时滞τ的变化出现多个波峰和波谷,即部分时滞可诱导网络产生显著的随机多共振行为.但随pdelay增大,如pdelay=0.2,0.3,Q的最大值和其所对应的时滞区间逐渐减小.而当pdelay增大到一定程度,如pdelay=0.5,0.7,1,Q的最大值逐渐减到最小,且其对应的时滞τ取值区间仅在系统固有周期T的整数倍附近.由此可以看出,部分时滞可诱导网络产生随机多共振行为,并且随pdelay增大系统最佳响应Q值和其对应的时滞取值区间逐渐减小,即多共振行为逐渐减弱.

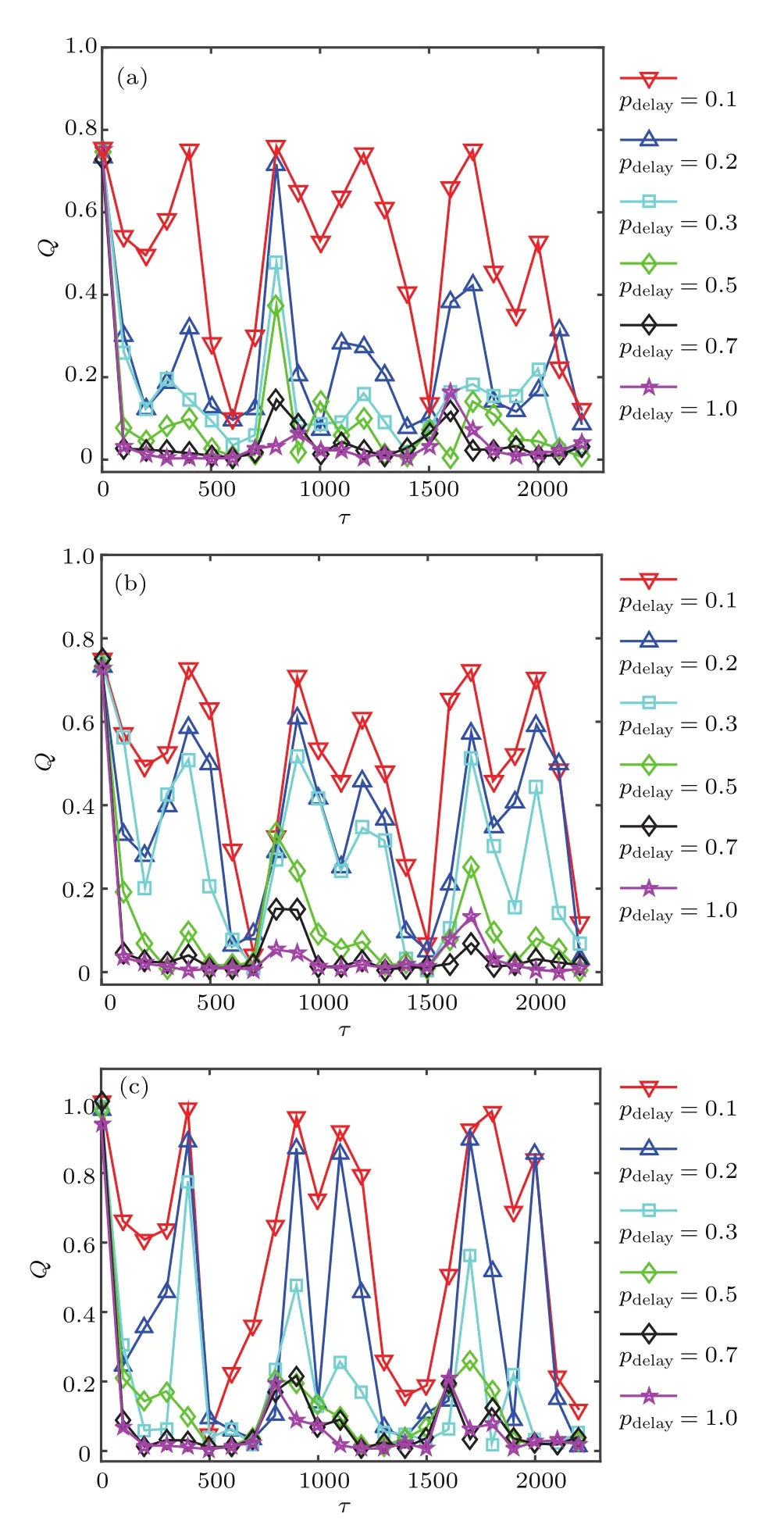
图8 (网刊彩色)不同f下,响应强度Q随时滞τ的变化 (a)f=0.1,σ =0.025;(b)f=0.5,σ =0.045;(c)f=0.9,σ=0.06;其他参数为fb=0.8Fig.8.(color online)Dependence of response amplitude Q with respect to partial time delay τ for different time delay pdelayin the different hybrid networks:(a)f=0.1,σ =0.025;(b)f=0.5,σ =0.045;(c)f=0.9,σ=0.06.Other parameter is fb=0.8.

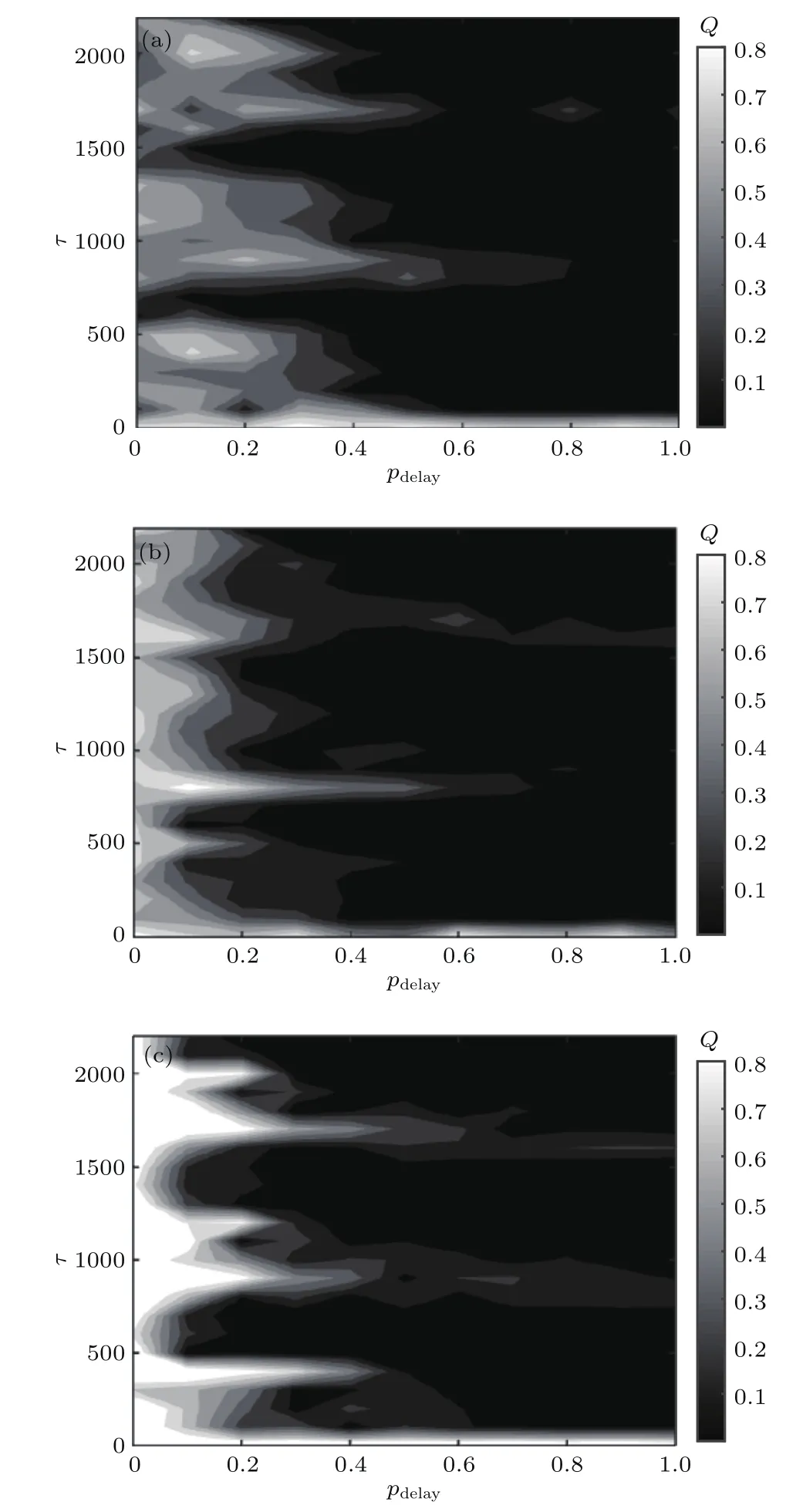
图9 不同情况下,响应强度Q随时滞τ和概率pdelay变化的等高线图 (a)f=0.1,σ=0.025;(b)f=0.5,σ=0.045;(c)f=0.9,σ=0.06;其他参数为fb=0.8Fig.9.Dependence of response amplitude Q with respect to time delay τ and probability pdelayfor different hybrid networks:(a)f=0.1,σ =0.025;(b)f=0.5,σ =0.045;(c)f=0.9,σ=0.06.Other parameter is fb=0.8.

为了进一步研究部分时滞对系统响应Q的影响,在二维参数平面观察了Q随τ和pdelay的变化趋势,如图9所示.观察图9(a)—(c)发现,部分时滞对系统响应Q的影响基本保持一致.当pdelay较小时,如pdelay＜0.3,随τ增加平面内交替出现三个明显的白色带状区域,说明部分时滞诱导网络产生随机多共振行为.并且发现随pdelay增加,白色区域颜色逐渐变深,即Q值变小且带状区域逐渐变窄;当pdelay＞0.3时,带状区域仅在系统固有周期T=820的整数倍附近隐约可见.此外,随f增大,较小的pdelay所对应的白色区域颜色越来越浅,即系统响应强度Q值越来越大,从而说明若混合突触网络中化学突触较多时,相比电突触耦合部分时滞能诱导产生更强的随机多共振行为.综上,部分时滞可诱导网络产生随机多共振行为,并且存在一个阈值pdelay≈0.3,当网络中时滞边比例小于此阈值,能产生明显的多共振行为,并且系统最佳响应Q对应的时滞宽度较广;而当混合突触网络中时滞边较多时,仅在固有周期的整数倍附近才会产生弱的多共振行为.这一现象和我们之前对部分时滞的研究保持一致[40,41],所不同的是在整数倍附近随pdelay增大响应Q逐渐减弱.这主要是因为这里设定的是带有少量抑制性突触的混合突触网络,之前有研究显示在抑制性突触网络里共振发生在T/2的奇数倍附近,而在兴奋性突触网络里共振发生在T/2的偶数倍附近[41].因此,由于受部分时滞对抑制性突触的作用,当pdelay较大时整数倍附近的随机共振被抵消逐渐减弱;而在非整数倍附近,混合突触网络主要以兴奋性突触为主,由于部分时滞对兴奋性突触连接产生的共振有抑制作用,所以系统随机共振快速减弱.

3.3 部分时滞和噪声对随机共振的混合作用

基于以上分析可知随机共振通常发生在部分时滞为系统固有周期的整数倍附近,并且随网络中时滞边比例改变时,共振行为会发生明显变化.由此,本小节主要在整数倍时滞处,讨论不同混合突触网络中,系统响应Q随时滞边比例pdelay和噪声强度σ的变化趋势,如图10所示.这里选择化学突触比例f=0.1,0.5,0.9,部分时滞位于τ=0,820,1640处进行研究.如图10(a),(d),(g)所示,当τ=0时,f=0.1,0.5,0.9所对应的混合突触网络分别在其恰当的噪声强度处引起共振行为.而当τ=820时(图10(b),(e),(h)),最佳响应Q所对应的噪声宽度明显增大;当时滞继续增大到τ=1640(图10(c),(f),(i)),白色区域随之再次增大.这一现象说明,时滞越大,系统响应Q对应的噪声宽度越广,越能产生强的共振行为.此外,发现随pdelay增大,Q值逐渐增大,并且最佳Q所对应的噪声区间也逐渐增大(如图10(i)).类似地,在时滞相等时,随化学突触比例f增加,Q值相应变大并且白色区域更加显著(如图10(b),(e),(h)),进一步证实了图9的现象.为更好地观察上述现象,图11分别对比了不同f下整数倍时滞处最佳噪声σ的变化区间.当τ=0时,神经元网络内无时滞,因此与前面讨论的结果一致,使得神经元网络达到极大的最优噪声强度与pdelay无关,而是随f的增加而增加(如图11(a)所示);当τ增加且是单个Rulkov神经元周期的整数倍时,随τ的增大,最佳响应Q所对应的σ和pdelay的区域也将变大;并且,随f增大,最佳响应Q所对应的σ区间也逐渐增大.综上,兴奋性化学突触能提高网络的共振行为,f越大,最佳噪声区间越广.此外,在兴奋性突触为主的混合突触网络中时滞边越多,系统最佳响应Q的噪声区间越大,并且越能促进系统产生更有效的随机共振行为.

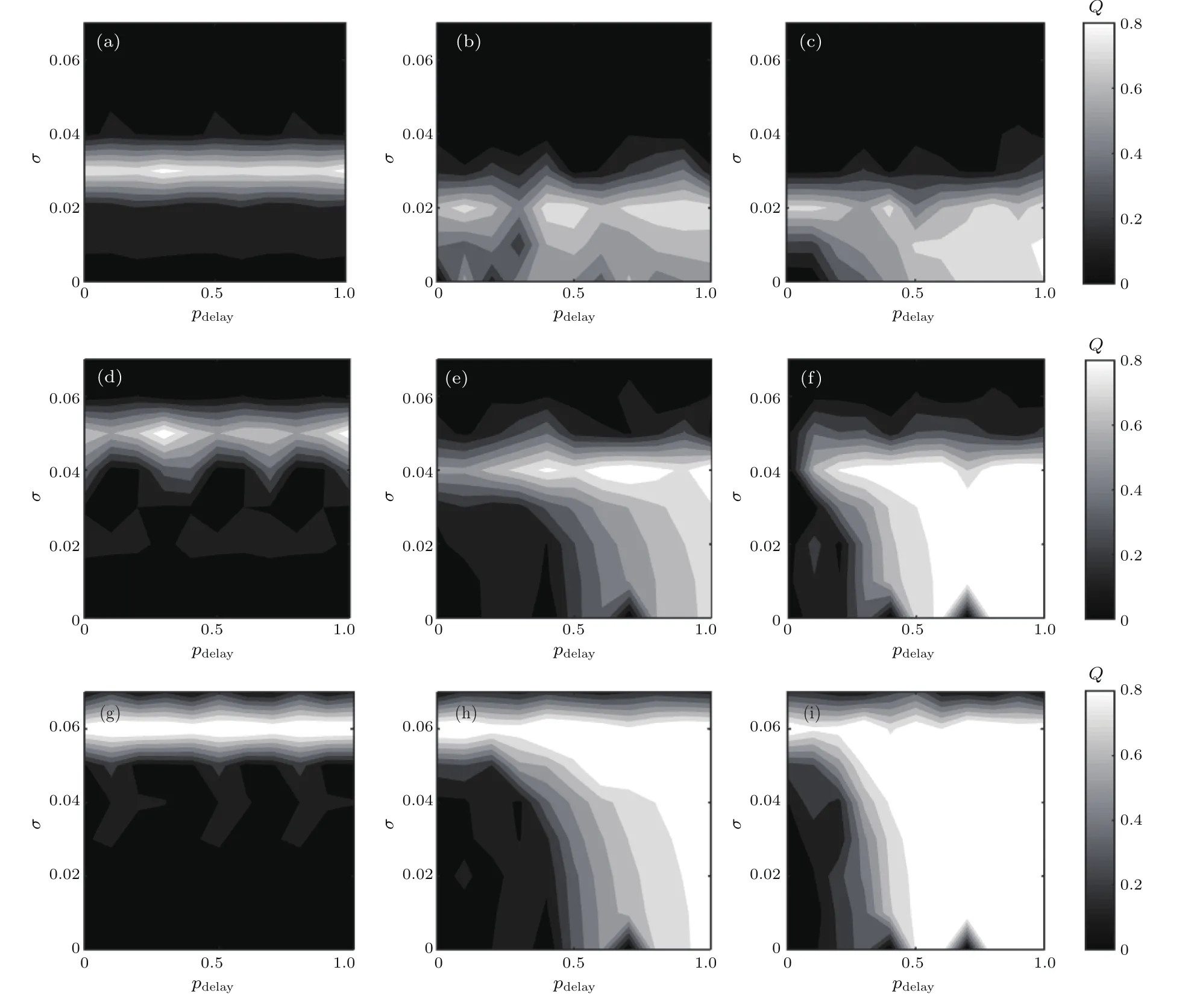
图10 不同化学突触比例下,整数倍时滞处响应强度Q随噪声强度σ和部分时滞概率pdelay变化的等高线图(a)f=0.1,τ=0;(b)f=0.1,τ=820;(c)f=0.1,τ=1640;(d)f=0.5,τ=0;(e)f=0.5,τ=820;(f)f=0.5,τ=1640;(g)f=0.9,τ=0;(h)f=0.9,τ=820;(i)f=0.9,τ=1640;其他参数为fb=0.8Fig.10.Dependence of response amplitude Q with respect to noise intensity σ and probability pdelayfor different probability of chemical synapse f:(a)f=0.1,τ=0;(b)f=0.1,τ=820;(c)f=0.1,τ=1640;(d)f=0.5,τ=0;(e)f=0.5,τ=820;(f)f=0.5,τ=1640;(g)f=0.9,τ=0;(h)f=0.9,τ=820;(i)f=0.9,τ=1640.Other parameter is fb=0.8.

图11 (网刊彩色)不同时滞τ下,系统最佳响应Q所对应的噪声取值σ随pdelay的变化 (a)τ=0;(b)τ=820;(c)τ=1640;其他参数为fb=0.8Fig.11.(color online)Dependence of noise intensity σ with respect to probability pdelayfor optimal Q on different probability of chemical synapse f:(a)τ=0;(b)τ=820;(c)τ=1640.Other parameter is fb=0.8.

4 总结及讨论

鉴于神经元在信息传递时不同的耦合作用以及时间延迟的影响,本文构建了带有电兴奋、电抑制、化学兴奋、化学抑制混合突触耦合的小世界神经元网络,研究部分时滞及噪声对混合突触作用下网络随机共振的影响.研究结果表明,噪声能诱导以兴奋性突触为主的混合突触耦合网络产生明显的随机共振行为;而在抑制性突触为主的混合突触网络中,由于抑制性电流的作用,噪声不能诱导产生随机共振;并且最佳噪声区间不会随兴奋性和抑制性突触比例的不同而改变.更有趣的是,在以电耦合为主的混合突触网络里,兴奋性突触比例超过一定阈值,即可存在恰当的噪声区间使系统产生随机共振行为;而在以化学耦合为主的混合突触网络里,仅当兴奋性突触与抑制性突触存在恰当比例,约为4:1达到E-I平衡状态时,噪声才可诱导网络产生共振行为.由此,在后面的研究中我们设置fb=0.8,即网络为E-I平衡状态进行研究.结果显示系统最佳噪声强度σ随化学突触比例f的增加呈线性增长关系.特别地,在某些较大的化学突触比例附近,会存在两个最优的噪声区间促使系统发生随机双共振行为.进一步,研究了部分时滞对随机共振的影响.研究发现,随网络中时滞边比例的改变,部分时滞能诱导网络产生随机多共振行为.当网络中时滞边比例小于阈值pdelay≈0.3,系统最佳响应Q对应的时滞宽度较广;而当混合网络中时滞边较多时,仅在固有周期的整数倍附近才会产生弱的多共振行为.并且网络中含有的化学突触越多,部分时滞诱导的多共振行为越强.此外,分析了噪声和部分时滞对共振行为的影响.数值结果指出在兴奋性突触为主的混合突触网络中化学突触所占的比例能提高最佳噪声区间和网络的共振行为;时滞越大,共振所对应的噪声区域越广;并且网络中存在的时滞边越多,越容易促使噪声和时滞诱导其产生明显的共振行为.

由于本文全面考虑了混合突触和部分时滞及噪声对共振的影响,其模型构建更符合实际神经元在网络中的存在形式.鉴于此,希望本研究能丰富神经科学的理论成果,尤其是对随机共振的研究产生一定的理论指导意义.但是,文中也存在很多不足之处,如神经元的耦合强度并不是固定的,即具有突触可塑性[47−49],但本文只考虑在耦合强度固定的情况研究.此外,脑网络是一个高度模块化功能网络[50,51].所以,部分时滞、混合突触等在具有突触可塑性的模块网络会对随机共振产生什么影响尚需进一步深入探讨.

[1]Longtin A,Bulsara A,Moss F 1991Phys.Rev.Lett.67 656

[2]Mori T,Kai S 2002Phys.Rev.Lett.88 218101

[3]Wang Q Y,Shi X,Lu Q S 2008Synchronization Dynamics in the Coupled System of Neurons(Beijing:Science Press)p99(in Chinese)[王青云,石霞,陆启韶2008 神经元耦合系统的同步动力学(北京:科学出版社)第99页]

[4]Benzi R,Sutera A,Vulpiani A 1981J.Phys.A:Math.Gen.14 L453

[5]Pikovsky A S,Kurths J 1997Phys.Rev.Lett.78 775

[6]Hanggi P 2002ChemPhysChem3 285

[7]Jung P,Mayer-Kress G 1995Phys.Rev.Lett.74 2130

[8]Sun X J,Perc M,Lu Q,Kurths J 2008Chaos18 023102

[9]Sun X J,Lu Q S 2014Chin.Phys.Lett.31 020502

[10]Zhou C S,Kurths J,Hu B 2001Phys.Rev.Lett.87 098101

[11]Zhou X R,Luo X S 2008Acta Phys.Sin.57 2849(in Chinese)[周小荣,罗晓曙 2008物理学报 57 2849]

[12]Wang M S,Hou Z H,Xin H W 2006Chin.Phys.23 2666

[13]Lin X,Gong Y B,Wang L 2011Chaos21 043109

[14]Ozer M,Perc M,Uzuntarla M 2009Phys.Lett.A373 964

[15]Liu Z Q,Zhang H M,Li Y Y,Hua C C,Gu H G,Ren W 2010Physica A389 2642

[16]Tessone C J,Mirasso C R,Torah R,Gunton J D 2006Phys.Rev.Lett.97 194101

[17]Li Y Y,Jia B,Gu H G,An S C 2012Commun.Theor.Phys.57 817

[18]Perc M 2007Phys.Rev.E76 066203

[19]Sudhof T C,Malenka R C 2008Neuron60 469

[20]Connors B W,Long M A 2004Annu.Rev.Neurosci.27 393

[21]Shi X,Wang Q,Lu Q 2008Cogn.Neurodynamics2 195

[22]Wang Q,Zhang H,Chen G 2012Chaos22 043123

[23]de Zeeuw C I,Holstege J C,Ruigrok T J H,Voogd J 1990Neuroscience34 645

[24]de Zeeuw C I,Hoogenraad C C,Koekkoek S K E,Ruigrok T J,Galjart N,Simpson J I 1998Trends.Neurosci.21 391

[25]Kopell N,Ermentrout B 2004Proc.Natl.Acad.Sci.USA101 15482

[26]Yilmaz E,Uzuntarla M,Ozer M,Perc M 2013Physica A392 5735

[27]Yu H,Guo X,Wang J 2017Commun.Nonlinear Sci.42 532

[28]Turrigiano G G,Nelson S B 2004Nat.Rev.Neurosci.5 97

[29]Wang Y,Sugita S,Sudhof T C,Biol J 2000J.Biol.Chem.275 20033

[30]Bückers J,Wildanger D,Vicidomini G,Kastrup L,Hell S W 2011Opt.Express19 3130

[31]Turrigiano G G,Nelson S B 2000Curr.Opin.Neurobiol.10 358

[32]Vogels T P,Sprekeler H,Zenke F,Clopath C,Gerstner W 2011Science334 1569

[33]Eichler S A,Meier J C 2008Front.Mol.Neurosci.1 PMC2526001

[34]Petrou M,Pop-Busui R,Foerster B R,Edden R A,Callaghan B C,Harte S E,Harris R E,Clauw D J,Feldman E L 2012Acad.Radiol.19 607

[35]Malina K C K,Jubran M,Katz Y,Lampl I J 2013J.Neurosci.33 8463

[36]Wang M L,Wang J S 2015Acta Phys.Sin.64 108701(in Chinese)[王美丽,王俊松 2015物理学报 64 108701]

[37]Gosak M,Markovic R,Marhl M 2012Physica A391 2764

[38]Wang Q,Perc M,Duan Z,Chen G 2009Chaos19 023112

[39]Yu H,Wang J,Liu C,Deng B,Wei X 2014Physica A405 25

[40]Sun X J,Li G F 2016Acta Phys.Sin.65 120502(in Chinese)[孙晓娟,李国芳 2016物理学报 65 120502]

[41]Sun X,Li G 2017Nonlinear Dynam.89 1

[42]Sun X,Perc M,Kurths J 2017Chaos27 053113

[43]Rulkov N F 2001Phys.Rev.Lett.86 183

[44]Landa P S,McClintock P V E 2000J.Phys.A:Math.Gen.33 L433

[45]Zaikin U A,García-Ojalvo J,Báscones R,Kurths J 2003Phys.Lett.A312 348

[46]Watts D J,Strogatz S H 1998Nature393 440

[47]Watt A J,Desai N S 2010Front.Synaptic.Neurosci.2 PMC3059670

[48]Song S,Miller K D,Abbott L F 2000Nat.Neurosci.3 919

[49]Toyoizumi T,P fi ster J P,Aihara K,Gerstner W 2007Neural.Comput.19 639

[50]Hilgetag C C,Burns G A P C,OŃeill M A,Scannell J W,Young M P 2000Philos.Trans.Roy.Soc.B355 91

[51]Hilgetag C C,Kaiser M 2004Neuroinformatics2 353