基于量子相干效应的无芯射频识别标签的空间散射场测量∗

闫丽云2) 刘家晟1)3) 张好1)3) 张临杰1)3) 肖连团1)3) 贾锁堂1)3)

1)(山西大学激光光谱研究所,量子光学与光量子器件国家重点实验室,太原 030006)2)(山西大学物理电子工程学院,太原 030006)3)(极端光学协同创新中心,太原 030006)

(2017年8月16日收到;2017年9月20日收到修改稿)

1 引 言

射频识别(RFID)技术最早出现于第二次世界大战,用来识别敌友战机.现在RFID技术已经被大量应用于各个领域,比如道路收费系统以及货物跟踪与识别等.目前所出现的无芯RFID标签,不需要在标签上使用芯片来编码数据,它根据不同标签的反向散射场具有不同的电磁特性来进行识别,引起了人们极大的兴趣,而无芯RFID标签的设计核心主要是标签上的散射单元.为了减小标签尺寸,散射单元同时具有天线和谐振单元的作用,不同尺寸的散射单元工作在不同的频率上.在平面波照射下,将会产生具有不同电磁特征的反向散射场.图1所示为四种不同形状的散射单元[1,2].研究无芯标签上散射单元的反向散射电磁特性所面临的困难之一就是对其空间散射场分布的精确测量.特别是随着散射单元的尺寸减小,远场散射场的测量过程中容易引入外界干扰,因此具有较大的测量不确定性.近年来,近场测量技术应用于目标散射特性的研究正受到越来越多的关注[3,4].

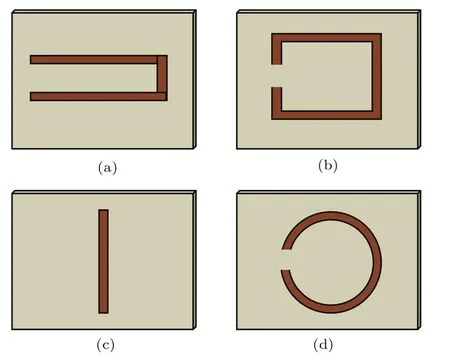
图1 不同形状的散射单元 (a)C形结构;(b)矩形开口谐振环;(c)线形结构;(d)圆形开口谐振环Fig.1.Scatterers having various shapes:(a) “C”-like structure;(b)rectangular SRR;(c)line-shape structure;(d)circular SRR.

近年来以原子蒸汽池作为测量电磁场的传感器,已经在磁场测量上获得了很好的灵敏度[5,6].而里德伯原子作为具有高激发态(主量子数n很大)电子的原子,它的显著特征是其轨道半径很大,具有较大的电偶极矩,因此里德伯原子对外电场很敏感,容易通过外电场实现里德伯原子量子态操控[7].2012年,Shaffer小组首次利用里德伯原子实现了对微波电场场强的高灵敏探测,获得了远高于基于传统的偶极振子测量的精度[8].最近该小组采用调制解调技术获得了3 µV·cm−1·Hz−1/2探测灵敏度[9].此后使用原子蒸汽池作为传感器,实现了远场情况下厘米波、毫米波的电场测量[10−14]以及原子蒸汽池内部电场空间分布特征高分辨成像[11,15−19].本文基于原子蒸汽池中铯里德伯原子的电磁感应透明(EIT)光谱在微波场作用下的Aulter-Towns(AT)效应,获得了图1(c)所示的标签上的线形散射单元的散射场的空间分布的亚波长高分辨测量,并实现了线形散射单元与入射射频电场极化方向不同夹角的有效分辨.本实验首次演示了线形散射单元的近场散射空间分布的亚波长分辨率的测量,对于无源标签理论计算模型的完善、实现无芯射频识别标签的设计和识别具有重要的应用价值.

2 实验设置

图2为实验涉及的铯原子的四能级系统示意图.里德伯态51D5/2–50P3/2的跃迁与被测标签的设计响应频率基本一致.实验装置如图3所示[18,19],探测光来自于半导体激光器(DL pro,Toptica),首先被锁定在超稳腔(ATF-6010-4,Stable Laser System)上,探测光线宽小于10 kHz.然后通过声光调制器将激光频率移动到铯原子6S1/2(F=4)→6P3/2(F′=5)的共振跃迁线上.510 nm耦合光来自倍频激光器(TA-SHG pro,Toptica),输出频率可以在6P3/2(F′=5)→51D5/2共振频率附近连续调谐.两束激光在铯蒸气池内沿着相反方向传输且重合.耦合光的功率为25 mW,探测光功率为5µW.两光束的直径分别为360µm和494µm,为保证原子蒸汽池内的光束直径尽可能均匀,束腰被置于铯蒸汽池中心.探测光通过原子蒸汽池后进入光电探测器.实验中在里德伯态共振频率附近扫描耦合光的频率,示波器上可以观察到里德伯原子EIT光谱.

图2 铯里德伯原子的四能级系统Fig.2.The four-levels system of Cs Rydberg atoms.

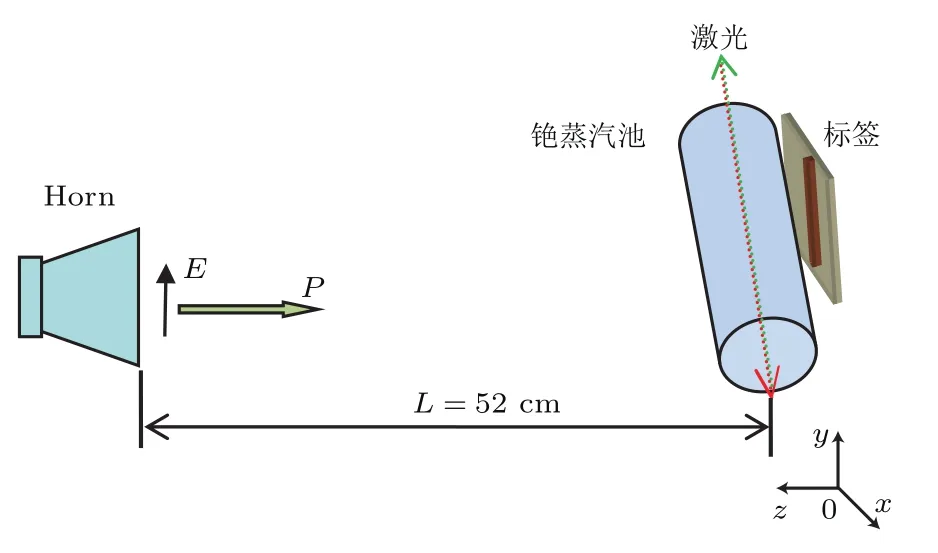
图3 实验装置图Fig.3.The scheme of experiment setup.

待测的具有线形散射单元的无芯RFID标签放置在铯蒸汽池后面,散射单元中心与蒸汽池轴线平齐.微波电场由微波信号发生器产生,实验中微波发射器输出功率被设置为0 dBm.通过标准增益矩形喇叭天线(LB-180400-KF,A-INFO)将频率为5.366 GHz的垂直极化的平面波辐射到铯蒸汽池和无芯RFID标签上.喇叭与铯蒸汽池距离52 cm,满足微波电场辐射的远场条件.实验所使用铯蒸汽池是圆柱形,截面直径为20 mm,长度为50 mm,池壁厚度为1 mm.蒸汽池的材料是硼硅玻璃,其介电常数为2.165.实验被测无芯RFID标签是边长为22.5 mm的方形标签,介质是厚度为0.8 mm的罗杰斯4350,介电常数为3.66.标签采用单面的线形贴片作为散射单元,长度为20 mm,宽度1 mm.标签谐振频率由线形贴片的长度和介质的介电常数决定,关系如(1)式所示:

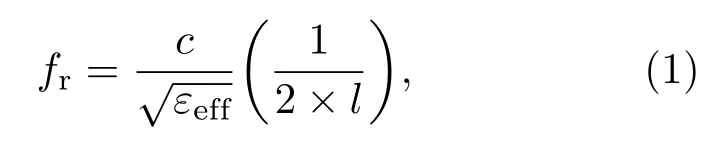
其中,fr为标签的谐振频率,c为光速,εeff为贴片介质的有效介电常数,l为线形贴片的长度.

实验中所制作标签的谐振频率为5.3 GHz,响应带宽约100 MHz.实验首先测量了无标签时铯蒸汽池中y和z两个方向的电场强度分布.然后按照如图4所示的四种放置方式将标签放置在原子蒸汽池后面,标签与蒸汽池间距小于1 mm.分别对线形散射单元与微波电场极化方向夹角α为0°,45°,90°,135°情况下的线形散射单元的反向散射的场强进行测量.测量中,光束相对于铯蒸汽池中心分别在y,z方向上进行移动,以获得该线形散射单元的二维空间反向散射场强度.因为两激光束的最大直径为494µm,被测微波的波长λMW为5.59 cm,被测微波场二维空间分辨率可达到λMW/12[17−19].

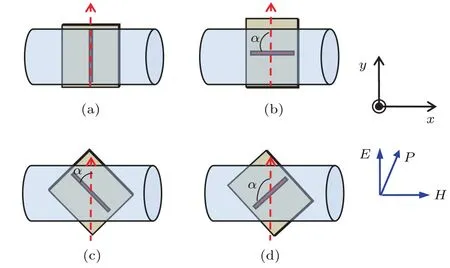
图4 实验中标签的四种放置方式 (a)α=0°;(b)α =90°;(c)α =45°;(d)α =135°Fig.4.Four placement con fi guration of the tag:(a)α =0°;(b)α =90°;(c)α =45°;(d)α =135°.

3 实验结果与分析

图5(a)是实验获得的无微波电场作用下的铯里德伯原子EIT效应光谱.在频率为5.366 GHz的微波电场作用下,观测到EIT光谱发生了分裂,如图5(b)所示.实验中EIT光谱的AT分裂间隔Δf与探测光所在位置处的微波电场强度关系如(2)式所示[10,11]:

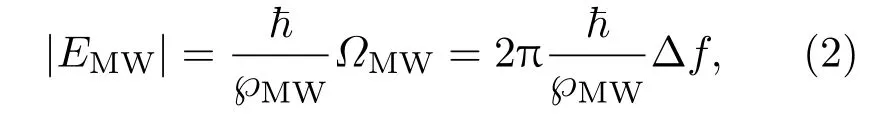
式中EMW为微波射频电场强度;ħ为约化普朗克常数;ΩMW为微波电场的拉比频率;℘MW为微波电场对应的里德伯态的原子跃迁偶极矩,此处51D5/2–50P3/2的跃迁偶极矩等于1715ea0,其中e为元电荷,a0是玻尔半径.通过(2)式可知,可以通过测量EIT-AT分裂光谱的间隔Δf来获得微波电场的强度值.

实验中使用的标准增益喇叭天线沿−z轴方向发射垂直极化的平面波,垂直入射到线形标签上,线形贴片与入射波的电场方向间的夹角为α.反向散射电场在水平方向的分量和垂直方向的分量如(3)和(4)式所示,其中k为比例系数,Ei(x,y,z)为标签的入射场强,其大小符合电磁波自由空间传播模型,即Ei(x,y,z)与天线的发射场强成正比,与入射点和发射天线之间的距离成反比.

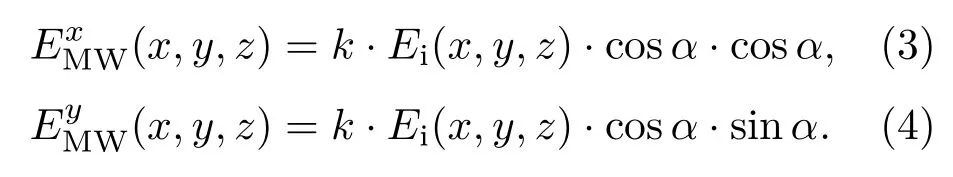
从(3)和(4)式可看出空间中任意位置处的标签散射电场EMW(x,y,z)的大小和线形散射单元与入射微波电场的极化方向之间的夹角α以及该位置处入射电场Ei(x,y,z)有关.

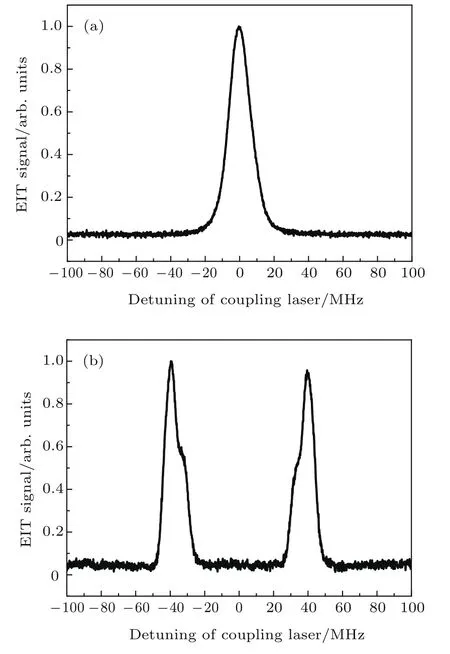
图5 (a)未加微波场情况下的EIT透射峰;(b)微波场作用下的EIT-AT分裂光谱Fig.5.(a)EIT transmission signal without microwave electric fi eld;(b)the EIT-AT splitting spectrum when a microwave electric fi eld is applied.

图6所示为光束相对于铯蒸汽池中心(被定义为坐标原点,坐标系如图3所示),沿z轴前后移动±4 mm范围,测量间隔为0.5 mm时得到的电场强度分布情况.图7所示为光束相对于铯蒸汽池中心,沿y轴上下移动±3.5 mm范围,测量间隔为0.2 mm时电场强度分布的结果.其中离散点为实验测量结果,与之同颜色的实线为利用电磁仿真软件进行的理论仿真结果,可以看到实验结果与仿真数据的变化趋势基本符合.若标签以不同角度放置在铯蒸汽池后面,其散射场会随着标签上线形散射单元与入射场的夹角α的变化而改变[2],变化规律符合(3)和(4)式.当标签垂直放置,即线形散射单元与入射电场夹角为0°,其散射场最大,如图中红色圆点曲线所示.当标签水平放置,即线形散射单元与入射电场夹角为90°,其散射场最小,如图中绿色三角曲线所示,与无标签时的测量结果很接近.若标签以45°和135°这两种放置方式,由于互相对称,其散射场强的幅度基本上相等,如图中青色和蓝色曲线(点线)所示.同时图6的结果显示,在标签角度为0°,45°和135°时z轴即微波场传输方向上场强分布有增加的趋势.这是由于随着z轴取值的增加,被测位置更加靠近标签,标签散射场的强度更大,这与无标签时电场分布的测量结果展现出明显不同的规律.图7显示了y轴即竖直方向上的场强的分布.理论拟合计算考虑了入射微波电场在远场近似下为平面波和标签反射的近场的分布,此时在竖直方向上的电场分布基本不变.而实验数据中在标签角度为45°和135°时有上扬的趋势,我们认为是射频标签的反射场与铯蒸汽池壁的相互作用造成,因为铯蒸汽池顶端有尖端结构,这导致了在靠近尖端位置附近的电场分布不均匀.由图6和图7可以看出,在标签放置角度改变的情况下,通过对空间中两个正交方向上的电场分布进行高分辨测量,获得了具有明显差异的强度曲线,由此可以通过强度曲线获得标签散射单元有效的角度信息.

图6 (网刊彩色)激光光束沿z轴前后移动时,标签在不同放置方式下的散射场强Fig.6.(color online)Simulation and experimental data of backscattered electric fi eld of the tag on the z-axis.

图7 (网刊彩色)激光光束沿y轴上下移动时,标签在不同放置方式下的散射场强Fig.7.(color online)Simulation and experimental data of backscattered electric fi eld of the tag on the y-axis.

4 结 论

基于原子蒸汽池中铯里德伯原子的EIT光谱在微波场作用下的AT效应,利用原子蒸汽池作为传感器实现了对无芯RFID标签散射场近场场强的空间分布的高分辨测量,同时获得了亚波长的空间场强分辨率测量以及线形标签与入射微波电场极化方向夹角的有效分辨.本研究对于无芯RFID标签的散射单元的研究和设计有非常重要的意义.

[1]Vena A,Perret E,Tedjini S 2011IEEE Trans.Microw.Theory Tech.59 3356

[2]Yan L Y,Zhang W M 2016J.Test Measur.Technol.30 62(in Chinese)[闫丽云,张文梅 2016测试技术学报 30 62]

[3]Cown B J,Ryan C J 1989IEEE Trans.Antennas Propag.37 576

[4]Wu Y,Xue Z,Ren W,Li W M,Xu X W 20126th Asia-Paci fi c Conference on Environmental Electromagnetics(CEEM)Shanghai,China,November 6–9,2012 p72

[5]Kominis I K,Kornack T W,Allred J C,Romalis M V 2003Nature422 596

[6]Savukov I M,Seltzer S J,Romalis M V,Sauer K L 2005Phys.Rev.Lett.95 063004

[7]Gallagher T F 1994Rydberg Atoms(Cambridge:Cambridge University Press)p11

[8]Sedlacek J A,Schwettmann A,Kübler H,Löw R,Pfau T,Shaffer J P 2012Nat.Phys.8 819

[9]Kumar S,Fan H Q,Kübler H,Jahangiri A J,Shaffer J P 2017Opt.Express25 8625

[10]Gordon J A,Holloway C L,Schwarzkopf A,Anderson D A,Miller S,Thaicharoen N,Raithel G 2014Appl.Phys.Lett.105 024104

[11]Fan H Q,Kumar S,Daschner R,Kübler H,Shaffer J P 2014Opt.Lett.39 3030

[12]Fan H,Kumar S,Sheng J,Shaffer J P,Holloway C L,Gordon J 2015Phys.Rev.Appl.4 044015

[13]Li J K,Yang W G,Song Z F,Zhang H,Zhang L J,Zhao J M,Jia S T 2015Acta Phys.Sin.64 163201(in Chinese)[李敬奎,杨文广,宋振飞,张好,张临杰,赵建明,贾锁堂2015物理学报64 163201]

[14]Anderson D A,Miller S A,Raithel G 2016Phys.Rev.Appl.5 034003

[15]Horsley A,Du G X,Treutlein P 2015New J.Phys.17 112002

[16]Bohi P,Treutlein P 2012Appl.Phys.Lett.101 181107

[17]Holloway C L,Gordon J A,Schwarzkopf A,Anderson D A,Miller S A,Thaicharoen N,Raithel G 2014Appl.Phys.Lett.104 244102

[18]Zhou J,Zhang W Q,Hao Y M,Jin T,Jiang X H,Zhang H,Zhang L J 2016J.Quantum Opt.22 311(in Chinese)[周健,张玮茜,郝艳梅,金桐,蒋徐浩,张好,张临杰2016量子光学学报22 311]

[19]Liu J S,Zhang H,Song Z F,Zhang L J,Jia S T 2016IEEE MTT-S International ConferenceBeijing,China,July 27–29,2016 p1