负带隙HgCdTe体材料的磁输运特性研究∗
2018-01-18沈丹萍张晓东孙艳康亭亭戴宁褚君浩俞国林
沈丹萍 张晓东 孙艳 康亭亭 戴宁褚君浩 俞国林
1)(东华大学理学院,上海 201620)2)(中国科学院上海技术物理研究所,红外物理国家重点实验室,上海 200083)
(2017年6月14日收到;2017年9月1日收到修改稿)
1 引 言
HgCdTe具有闪锌矿型晶体结构,其能带结构随Cd原子的组分而变化[1].当Cd组分位于临界点xc=0.165时,Hg1−xCdxTe的导带与价带在Γ点重合,成为带隙为零的半金属[2].当x>0.165时,其能带结构与具有正常能带序的CdTe类似,是一种典型的窄禁带半导体,其带隙刚好对应于红外波段且具有良好的可调控性,因而被广泛应用于红外探测器[3−5].当0≤x<0.165时,Hg1−xCdxTe能带结构与HgTe类似,具有倒置型能带序.张守晟团队[6]率先在HgTe/HgCdTe量子阱中预言了量子自旋霍尔效应的存在,并通过实验得到证实[7],极低温下在此结构中可以观察到拓扑绝缘导电态.近期的研究表明,通过对HgTe/HgCdTe量子阱施加较高的压应力,其带隙可达55 meV,有望实现高温拓扑绝缘体[8].
近年来,自旋器件因其独特的性质越来越受到人们的关注[9,10],如何在半导体材料中操纵电子自旋是材料研究中的一个热点.Chen等[11]则通过红外磁光谱研究了ZrTe5在外加磁场下从Dirac半金属到拓扑线节点半金属的转变过程中朗道能级分裂变化,微小的外加磁场就能使三维Dirac费米子产生相当大的Zeeman效应.Kretinin等[12]则研究了高质量InAs纳米线中强耦合量子点的近藤效应,发现由于InAs中存在强自旋-轨道耦合作用,磁场对近藤效应的抑制作用要远高于Zeeman分裂中g因子的影响.这些近期的研究成果都是围绕磁场对电子自旋的调控作用展开的,为我们的研究提供了一定的指导.
对HgCdTe这类窄禁带半导体而言,其自旋-轨道耦合作用是一项研究重点.HgCdTe的自旋-轨道耦合作用与带隙有着密切联系,随着带隙的减小,自旋-轨道耦合作用增强.魏来明等[13]利用零场附近的反弱局域现象,得到Hg0.77Cd0.23Te中零场自旋分裂能约为3.3 meV;高矿红等[14]则发现Hg0.78Cd0.22Te薄膜反型层中的自旋分裂能可以通过栅极电压在6.95—9.06 meV之间进行调控.而在HgTe/HgCdTe量子阱中仇志军等[15]发现其Rsshba自旋分裂能可达28.2 meV.可见HgCdTe是制备自旋电子器件的有力候选材料之一.
目前,对Cd组分小于临界点xc=0.165的倒置型能带序HgCdTe体材料的研究还鲜有报道.本文通过单晶生长了Cd组分为0.1的p型HgCdTe体材料,然后在其表面通过阳极氧化的方法使氧化层与体材料界面交界处形成反型层,制备了具有倒置型能带序的HgCdTe场效应器件.利用磁输运测试,在样品中观察到了量子霍尔平台效应和Shubnikov-de Haas(SdH)振荡效应.通过分析SdH振荡效应,得到样品的零场自旋分裂能约为26.55 meV.
2 实 验
通过单晶生长制备了Hg0.9Cd0.1Te体材料.将样品在碱性溶液中进行阳极氧化[16],使其在表面形成厚度约为80 nm的氧化层.该氧化层有两种效果:一是能够将样品表面与外界空气隔离以保护样品;二是将HgCdTe体材料表面钝化,从而在氧化层与HgCdTe体材料交界处形成反型层,即二维电子气.
采用范德堡测试方法[17],将样品切成5 cm×5 cm的方块,在方块的四个顶角上用金属铟制作四个电极以形成欧姆接触.测试在低温超导磁体系统中进行,磁场垂直于样品表面,温度维持在1.5 K.给样品通以rms值为1µA和频率为13.333 Hz的低频交流电流,再通过锁相放大器来测量磁阻值以获得样品的各项磁输运参数.
3 实验结果与讨论
图1给出了样品在温度为1.5 K时纵向磁阻ρxx和霍尔磁阻Rxy随磁场的变化.如图1所示,在高场范围内霍尔磁阻呈现出良好的量子霍尔平台,表明在氧化层与HgCdTe体材料交界处确实形成了二维电子气.在低场范围内,Rxy呈现类抛物线型变化;高场范围内,霍尔平台偏离了标准霍尔平台数值h/(ie2),这是由于样品内部存在着并联平行电导[18].该平行电导主要来源于HgCdTe体材料内的载流子.我们的样品是Cd组分为0.1的负带隙HgCdTe体材料,由于它本身的电阻非常小,二维电子气与之并联后呈现出的电阻就变得很小.这也是导致纵向磁阻ρxx在高场范围内本应该呈现的SdH振荡现象变为图1中曲线的原因.
由于低场范围内Rxy受到平行电导的干扰,其低场拟合直线严重偏离霍尔平台的中点,因此这里不采用线性拟合低场范围内Rxy随磁场的变化来获得霍尔浓度.通过分析纵向磁阻ρxx的SdH振荡来获得样品的载流子浓度及各项参数.为了更加清楚地研究SdH振荡的信息,对纵向磁阻ρxx进行了去背底处理,如图2所示.从图2观察到明显的拍频现象,在ν=12和ν=13之间出现了拍频节点.

图1 温度为1.5 K时,样品在垂直磁场下纵向磁阻ρxx(左轴)和霍尔磁阻Rxy(右轴)随磁场的变化Fig.1.The longitudinal(left scale)and transverse resistance(right scale)at 1.5 K.
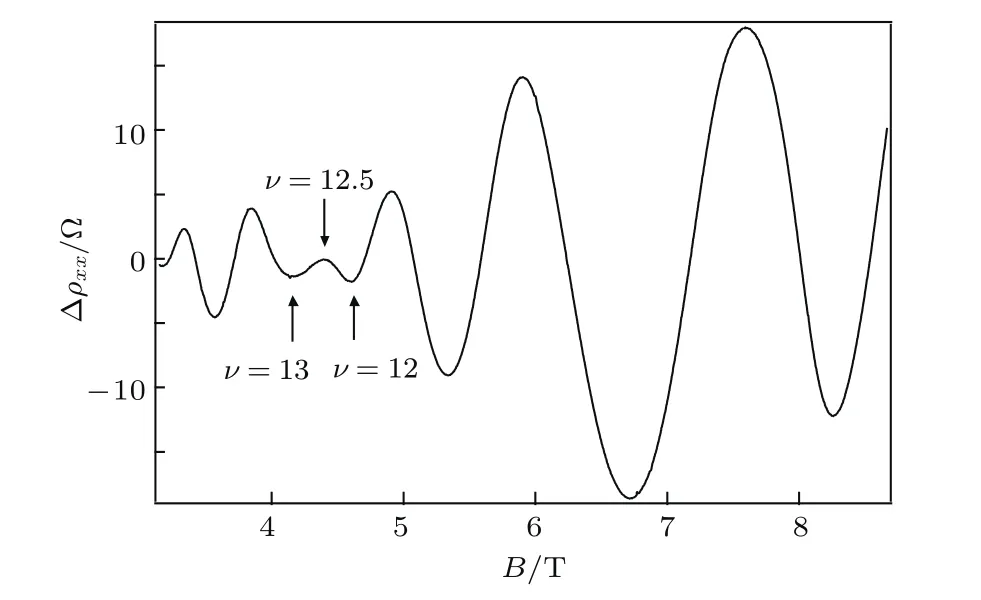
图2 对SdH振荡进行去背底处理后得到的变化曲线Fig.2.Remove the background resistance from SdH oscillations.
根 据 填 充 因 子ν= 2EF/(ħωc)及EF=(ħ代表普朗克常数,EF代表费米能级,ωc为电子的回旋共振频率,kF表示费米波矢,m∗是电子的有效质量)可以得出填充因子ν与磁场的倒数的关系式ν=hn/(eB).如图3所示,通过线性拟合填充因子ν随1/B的变化可以得到斜率k=hn/e=53.758,从而得到电子浓度n=1.3×1016m−2.从图3可以观察到拍频节点的位置正好处于ν=12和ν=13之间,推测其约为12.5.所有的点都基本在拟合直线附近,说明样品中不存在第二子带振荡,所得电子浓度也要低于仇志军等[15]在HgTe/Hg0.3Cd0.7Te量子阱中得到的浓度(1.86×1016m−2),表明本文的样品是单子带占据系统.
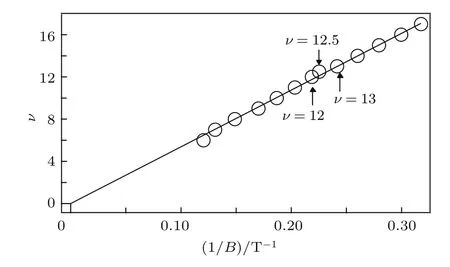
图3 填充因子ν随磁场的倒数1/B变化的拟合直线Fig.3.Filling fcator ν versus the reciprocal of the magnetic fi eld.
为了分析拍频现象的成因,进一步用快速傅里叶变换(fast Fourier transform,FFT)研究了SdH振荡曲线,如图4所示,从图中观察到明显劈裂的双峰,表明确实存在两个频率相近的振荡引起了拍频现象.引起拍频现象的原因主要有两个:一是零场自旋分裂;二是磁致子带间散射.仅凭拍频难以断定是自旋分裂的贡献还是磁致子带间散射的贡献[19].从SdH振荡的拟合分析中已发现本文的样品是单子带占据系统,而在单子带系统中不会出现磁致子带间散射,从而可以确定在样品中是零场自旋分裂导致了拍频现象的产生.因此可以从SdH振荡来分析样品的零场自旋分裂能及有效g因子.从FFT曲线峰值的对应频率可以计算样品电子浓度,由n=(f1+f2)e/h得到电子浓度为1.32×1016m−2,与前文所得电子浓度非常接近,说明我们的拟合直线是比较理想的.
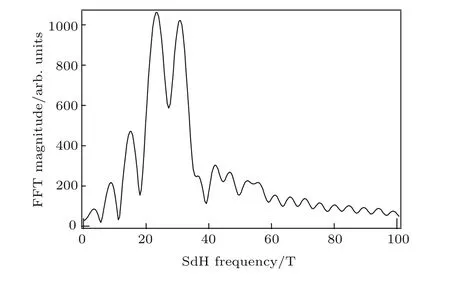
图4 SdH振荡曲线FFT结果Fig.4.Fourier transform of the SdH oscillations.
电子总自旋分裂包括Zeeman分裂、Rashba自旋-轨道耦合和Dresselhaus自旋-轨道耦合,拍频节点与这三种机制都有关系[20].与需要外加磁场才能产生Zeeman分裂不同,Rashba自旋-轨道耦合和Dresselhaus自旋-轨道耦合这两种由自旋-轨道耦合引起的自旋分裂在零磁场下就存在,因而被称为零场自旋分裂.当Rashba自旋-轨道耦合和Dresselhaus自旋-轨道耦合强度相当时,由于两者受时间反演转换影响,零场自旋分裂能近乎于零,拍频节点消失[20].图2中明显的拍频振荡表明必定是两者之一占据了主导作用.Dresselhaus自旋-轨道耦合主要由体反演不对称引起,而Rashba自旋-轨道耦合则主要由结构反演不对称引起.理论和实验研究都表明,对窄禁带半导体而言,电子的自旋分裂主要由结构反演不对称性引起[21].当电子浓度达到1016m−2时,倒置型能带序材料第一导带子带的重空穴特性会显著增强Rashba自旋分裂[15].因而在负带隙HgCdTe体材料中Rashba自旋-轨道耦合占具主导作用,Dresselhaus自旋-轨道耦合作用相对而言可忽略.
由上所述,电子的自旋分裂能包括零场自旋分裂能和Zeeman分裂能两个部分,一般可写为[22]
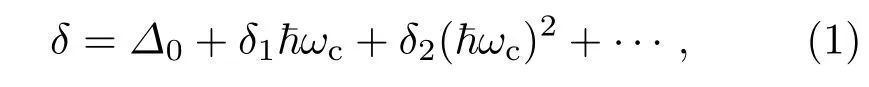
其中,右边第一项为零场自旋分裂能,第二项为一阶Zeeman分裂能,第三及以上项为高阶Zeeman分裂能项,电子的Zeeman分裂与总磁场成正比,在低场范围内高阶项可忽略.因而(1)式也可简单地近似写为[23]
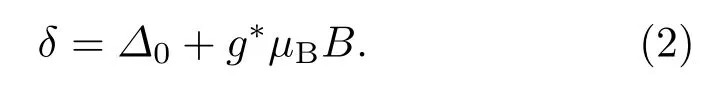
忽略Dresselhaus自旋-轨道耦合作用后,当单个自旋简并子带的自旋简并被由Rashba效应引起的零场自旋分裂解除时,如果自旋向上电子和自旋向下电子的浓度相近,则自旋向上电子的SdH振荡和自旋向下电子的SdH振荡的周期相近,叠加在一起就可能产生拍频.总振幅可以表示为自旋向上电子SdH振荡和自旋向下电子SdH振荡的叠加[24,25]:

其中E±=E±δ/2是自旋向上和自旋向下子带的能量.在(2)式的近似下,(3)式余弦项cos[2π(EF−E±)/(ħωc)−π] = cos[π(nh∓m∗Δ0/ħ)/(eB)∓πm∗g∗/(2m0)−π]关于1/B的频率分别为f±=(nh∓m∗Δ0/ħ)/(2e),由此得到Δ0=eħ(f−−f+)/m∗以及n=e(f++f−)/h,都与有效g因子无关.当根据Yang等[26]的报道取m∗=0.0185m0时,由上述FFT得到的自旋子带的SdH磁阻振荡频率差可以得到零场自旋分裂能Δ0=46.38 meV,比仇志军等[15]报道的HgTe/Hg0.3Cd0.7Te量子阱中的Rashba自旋分裂能(28.2 meV)更大.从带隙结构上讲,根据Laurenti等[27]的分析可以得到本文的样品在1.5 K时Eg=−0.124 eV,而HgTe在相同温度下Eg=−0.303 eV,因而本文的样品的零场自旋分裂能应该比仇志军等获得的结果小才合理.根据仇志军等[15]的报道m∗=(0.044±0.005)m0及Yang等[26]的报道m∗=0.0185m0做插值时得m∗=0.0323m0,则零场自旋分裂能Δ0=26.55 meV,小于仇志军等的结果且大于魏来明等[13]和高矿红等[14]的结果.Hg0.9Cd0.1Te的带隙宽度介于HgTe和Hg0.78Cd0.22Te之间,其自旋-轨道耦合强度应当也是介于两者之间,因而这一结果较符合从带隙结构而言的期望值.
根据(2)式与SdH振荡中的拍频节点可估算有效g因子.(3)式也可化为[18]

第一个余弦项是频率项,决定了总的SdH振荡的频率,第二个余弦项是振幅包络项.当零场自旋分裂Δ0存在时,振幅包络cos(πδ/ħωc)是1/B的周期函数.当|δ|/(ħωc)=n+1/2(n=0,1,2,···)时,振幅包络为零,出现拍频节点[22].因此可由拍频节点估算总自旋分裂能δ= ħωc(n+1/2)(n=0,1,2,···).根据Teran等[28]对拍频节点的分析,从图2观察到的拍频节点对应于δ=(3/2)ħωc,由此可得δ=23.62 meV.由(2)式得g∗=(δ−Δ0)/(µBB)=−11.54,小于仇志军等[15]得到的g∗=−18.2,但在同一个数量级,与零场自旋分裂能的趋势保持一致.Yakunin等[29]报道了具有倒置能带序的HgTe/Hg0.76Cd0.24Te量子阱中二维电子系统的自旋极化率,用重合法得到的结果是|m∗rg∗|=0.786.本文样品的自旋极化率|m∗rg∗|约为0.373,显然比Yakunin等的结果要小,主要是因为本文在低场范围内做了近似估算,而他们得到的是高场自旋极化率.高场范围内Zeeman分裂增强,有效g因子值增大,从而高场自旋极化率要大于低场自旋极化率.Zhang等[30]通过重合法得到的[001]方向的HgTe/HgCdTe量子阱中二维电子系统的自旋极化率在0.4到1.7之间,低场内的值与本文的结果比较接近,表明本文样品具有与HgTe类似的能带结构性质.g∗本身是自旋-轨道耦合直接导致的一个量,随着带隙的减小,自旋-轨道耦合作用增强,有效g因子不断减小,甚至变成负值[31].HgCdTe本身具有窄禁带的特点,而Cd组分为0.1时其带隙为负,价带与导带的耦合作用非常强,有效g因子的值与这一特质是相符合的.
4 结 论
通过分析负带隙HgCdTe体材料反型层中的SdH振荡现象,发现其具有非常大的零场自旋分裂能,约为26.55 meV,表明材料中存在强烈的Rashba自旋-轨道耦合.负带隙HgCdTe体材料所具有的倒置型能带序使其第一子能带具有重空穴特性以及强烈的自旋-轨道分裂,两者都导致了Rashba自旋-轨道耦合作用的增强.这些研究结果对今后设计和研发自旋电子器件提供了积极的实验基础.
[1]Hansen G L,Schmit J L,Casselman T N 1982J.Appl.Phys.53 7099
[2]Chu J H 2005Narrow-band Semiconductor Physics(Beijing:Science Press)p120(in Chinese)[褚君浩 2005 窄禁带半导体物理学(北京:科学出版社)第120页]
[3]Hu W D,Liang J,Yue F Y,Chen X S,Lu W 2016J.Infrared Millim.Wave35 25(in Chinese)[胡伟达,梁健,越方禹,陈效双,陆卫2016红外与毫米波学报35 25]
[4]Gawron W,Martyniuk P,Keblowski A,Kolwas K,Stepień D,Piotrowski J,Madejczyk P,Pedzińska M,Rogalski A 2016Solid.State.Electron.118 61
[5]Kopytko M,Rogalski A 2016Prog.Quant.Electron.47 1
[6]Bernevig B A,Hughes T L,Zhang S C 2006Science314 1757
[7]Konig M,Wiedmann S,Brune C,Roth A,Buhmann H,Molenkamp L W,Qi X L,Zhang S C 2007Science318 766
[8]Leubner P L,Lunczer L K,Brüne C T,Buhmann H T,Molenkamp L R W 2016Phys.Rev.Lett.117 086403
[9]Wolf S A,Awschalom D D,Buhrman R A,Daughton J M,Molnar S V,Roukes M L,Chtchelkanova A Y,Treger D M 2000Science294 1488
[10]Sarma S D 2001Am.Sci.89 516
[11]Chen R Y,Chen Z G,Song X Y,Schneeloch J A,Gu G D,Wang F,Wang N L 2015Phys.Rev.Lett.115 176404
[12]Kretinin A V,Shtrikman H,Goldhaber-Gordon D,Hanl M,Weichselbaum A,von Delft J,Costi T,Mahalu D 2011Phys.Rev.B84 245316
[13]Wei L M,Liu X Z,Yu G L,Gao K H,Wang Q W,Lin T,Guo S L,Wei Y F,Yang J R,He L,Dai N,Chu J H 2013J.Infrared Millim.Wave32 141(in Chinese)[魏来明,刘新智,俞国林,高矿红,王奇伟,林铁,郭少令,魏彦锋,杨建荣,何力,戴宁,褚君浩2013红外与毫米波学报32 141]
[14]Gao K H,Wei L M,Yu G L,Yang R,Lin T,Wei Y F,Yang J R,Sun L,Dai N,Chu J H 2012Acta Phys.Sin.61 027301(in Chinese)[高矿红,魏来明,俞国林,杨睿,林铁,魏彦锋,杨建荣,孙雷,戴宁,褚君浩2012物理学报61 027301]
[15]Qiu Z J,Gui Y S,Shu X Z,Dai N,Guo S L,Chu J H 2004Acta Phys.Sin.53 1186(in Chinese)[仇志军,桂永胜,疏小舟,戴宁,郭少令,褚君浩2004物理学报53 1186]
[16]Ahearn J S,Davis G D,Byer N E 1982J.Vac.Sci.Technol.20 756
[17]van der Pauw L J 1958Philips.Tech.Rev.20 220
[18]Buget M,Karavolas V C,Pceters F M,Singleton J,Nicholas R J,Herlach F,Harris J J,van Hove M,Borghs G 1995Phys.Rev.B52 12218
[19]Rowe A C H,Nehls J,Stradling R A 2001Phys.Rev.B63 201307
[20]Yang W,Chang K 2006Phys.Rev.B73 045303
[21]Das B,Datta S,Reifenberger R 1990Phys.Rev.B41 8278
[22]Das B,Miller D C,Datta S,Reifenberger R,Hong W P,Bhattacharya P K,Singh J,Jaffe M 1989Phys.Rev.B39 1411
[23]Wei L M 2012Ph.D.Dissertation(Shanghai:Shanghai Institute of Technical Physics,CAS)(in Chinese)[魏来明2012 博士学位论文(上海:中国科学院上海技术物理研究所)]
[24]Coleridge P T,Stoner R,Fletcher R 1989Phys.Rev.B39 1120
[25]Zhou Y M 2010Ph.D.Dissertation(Shanghai:Shanghai Institute of Technical Physics,CAS)(in Chinese)[周远明2010博士学位论文(上海:中国科学院上海技术物理研究所)]
[26]Yang R,Gao K H,Wei L M,Liu X Z,Hu G J,Yu G L,Lin T,Guo S L,Wei Y F,Yang J R,He L,Dai N,Chu J H,Austing D G 2011Appl.Phys.Lett.99 042103
[27]Laurenti J P,Camassel J,Bouhemadou A,Toulouse B,Legros R,Lusson A 1990J.Appl.Phys.67 6454
[28]Teran F J,Potemski M,Maude D K,Andrearczyk T,Jaroszynski J,Karczewski G 2002Appl.Phys.Lett.88 186803
[29]Yakunin M V,Podgornykh S M,Mikhailov N N,Dvoretsky S A 2010Physica E42 948
[30]Zhang X C,Ortner K,Pfeuffer-Jeschke A,Becker C R,Landwehr G 2004Phys.Rev.B69 115340
[31]Winkler R 2003Spin-Orbit Coupling Effects in Two-DimenionalElec-tronandHoleSystems(Berlin:Springer-Verlag)p133
