基于时变小世界模型的航空网优化评估∗
2018-01-18韩定定姚清清陈趣钱江海
韩定定 姚清清 陈趣 钱江海
1)(华东师范大学信息科学技术学院,上海市多维度信息处理重点实验室,上海 200241)
2)(上海电力学院数理学院,上海 200090)
(2017年5月12日收到;2017年7月4日收到修改稿)
1 引 言
航空网络的设计是一个在成本和旅客满意度之间进行平衡的复杂优化问题,决定了航空运输的效率.航空公司追求低成本、高收益,总是希望通过合理的网络优化,用更少的航班来满足市场需求;另一方面,要提高旅客的出行满意度抢占市场,必须尽可能地缩短旅客的飞行时间和转机次数,但会增加航空公司的建设、运营成本.两者的利益冲突导致了航线网络规划和航班计划编制的复杂性.航线网络结构设计是航空公司航班运营的基础.传统的航空网络优化,通常以整个航空公司的利润最大化或成本最小化作为优化目标函数.根据实际的座位数、飞机利用率、旅客流量、市场份额以及航班频率整数性等约束关系建立混合整数规划模型,求解最优航线结构及航班频率[1−5].由于实际的航线还要考虑例如机型指派、机组调配、燃油费用等现实问题,尽管上述优化模型能够较为准确地描述网络优化的本质,但在实际应用中仍存在极大的局限.特别地,此类问题的求解往往是NP-hard问题,对于大规模网络的优化问题难以给出精确的最优解.
近年来网络科学的兴起为研究航空网这一类开放的复杂系统提供了一个崭新的视角.将机场视为一个节点,两个机场之间的航线视为连边,每个航线上的运量或者航班频次视为边权,可以将航空运输系统抽象成静态的复杂加权网络.对世界、北美、欧洲以及中国等众多航空网络的实证研究已经证实:航空网是典型的具有无标度特征的空间小世界网络[6−13].网络功能和效率取决于它的拓扑,因此根据航空网的统计特征构建的简化模型是讨论空间网络优化问题的有力工具.通过在节点间合理地添加长边可以有效改善网络的全局传输效率[14−16].以Kleinberg为代表的学者详细讨论了空间小世界网络的最优导航问题,揭示了空间结构的变化对网络平均最短路径的影响[17−19].由于在航空网等现实交通系统的建设中,开辟一条新的线路所耗费的成本往往正比于其地理距离.文献[20—23]研究了在有限的成本预算下,如何通过合理地配置捷径来实现成本和导航效率的平衡.而Gastner和Newman[24]则将构网成本T与旅行成本Z作为构建空间网络的两个主要考虑因素,以成本函数E=T+γZ最小化作为优化目标,来求解网络的最优拓扑.上述研究基于对网络空间结构的考虑,为现实航空网络的优化设计提供了重要的理论支持.
时变性是航空网络的另一个重要特征.长期以来,对航空网络的研究通常假设网络本身具有相对的时空稳定性,而忽视了航班飞行计划的时序对实际旅行时间的影响.事实上,每条航线上的航班根据事先拟定的时刻表运行,由同一时刻所有处于飞行状态的航班构成的瞬时航班网络是动态变化的.作为航空运输的载体,航班网络才是决定实际运输效率的关键,而航线拓扑作为航班网络的聚合,并不能真实反映航空网络的运输功能.经过高度优化设计的航线结构必须辅以高效的航班计划,才能充分发挥网络空间结构的便利性.近来针对时变网络的研究证实,在时变条件下,无论是网络连接度、故障鲁棒性等基本属性,还是传播阈值、最优导航结构等动力学行为都明显不同于基于静态网络的传统认知[25−30].另一方面,出于成本的考虑,航班计划的编制充分考虑了航距这一空间因素的影响,因此航空网的空间结构和连边动力学之间具有潜在的时空关联特征.准确把握航空网络的时变行为,考虑航线结构和航班计划的综合作用,并据此实现网络的整体优化设计,将有助于航空公司构建具有竞争力的运营结构,并实现运输资源的优化配置.
本文首先实证航空网的时空关联行为,从连边活跃度驱动的角度构建一类契合航空网特征的时变空间小世界网络,讨论时空耦合强度对网络最优结构指数的影响;继而以成本最小化作为主要的优化目标,提出一种可以快速评估航线结构优化情况的方法;据此,可以根据航线客流的分布情况,快速推算出航线网络的最优拓扑及其相应的航班频率分布.
2 航空网的时空关联特征
作为一个典型的二维空间网络,航空网络中的节点,即机场,都具有明确的地理坐标.每条航线的航距也是网络设计时一个重要的考虑因素.本文首先从Open-Flights项目(http://open fl ights.org/data.html)中获取了所有机场的经纬度信息,并由下式计算每条航线的理论航距rij:
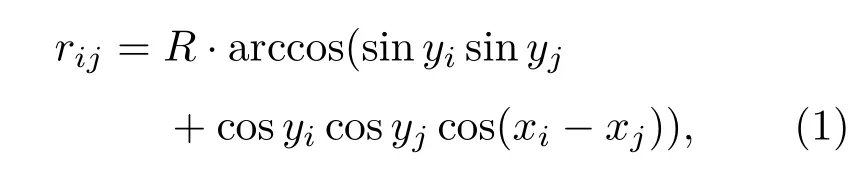
其中R为地球半径;(xi,yi),(xj,yj)分别为航线两端的机场i,j的经纬度.本节以英国航空公司和奥地利航空公司这两个特定航空网络为例,讨论航班密度与航线结构之间的关系.具体的航班信息可从官方网站(http://www.britishairways.com,http://www.austrian.com)公布的航班时刻表中提取.在同一条航线上,一天内可能有多个起降航班,因此在特定的时间尺度下,如每天,所有直飞的航班和通航机场构成了实际的航空网络,且该网络具有时变特征.再者,一条航线上累积飞行的航班数量能够有效反映本航线的繁忙程度.大量实证研究已经证实,航空网络具有异质特征,各个机场的吞吐能力和重要性存在极大的差异[6,9].每条航线的航距作为运输成本的重要考量因素之一,也会对航班密度产生影响.以英国航空网为例,选定网络中的枢纽节点LHR(London Heathrow)机场以及与其有航班联系且度值k=3的其他机场(Dublin(DUB)机场、Frankfurt(FRA)机场、Zürich(ZRH)机场、Prague(PRG)机场、Ras Al Khaimah(RAK)机场),从表1中不难看出,空间距离与航班密度之间确实存在某种约束,航距越大,航线上的航班密度相应较小,这也符合人们的直观感受.短程航线的设计往往以通勤为目标,因此这类航班通常采用一些支线小型飞机,几乎每日都有,非常稳定.而长程航线的设计主要是为了维系重要城市之间的经济、社会往来,但运行成本较高,因此通常采用一些大型干线飞机,但班次相对较少,每日航班差异较大,也更容易受到节假日等外在因素的影响.
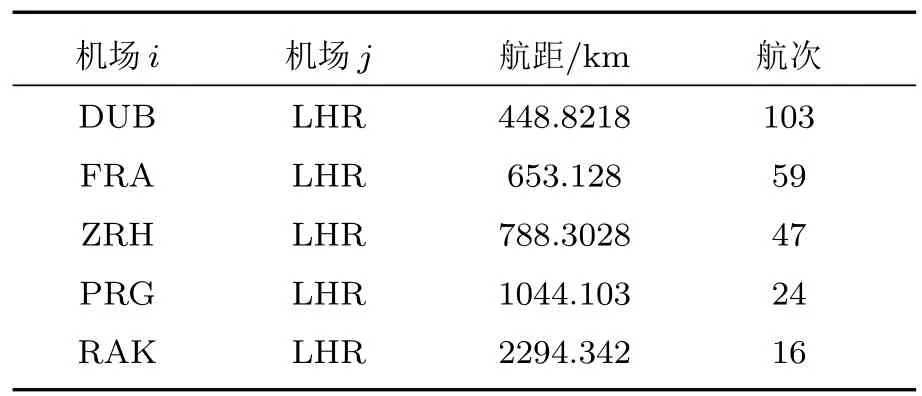
表1 英国航空公司航距与一周累积航次的关系Table 1.Dependence of the weekly cumulated fl ights on route distances in British Airways.
为了进一步确定航班密度(时间维度)和航线距离(空间维度)的关联特征,剔除网络的异质性对航班频率的影响,定义归一化航班密度为nl=Nl/(kikj),其中l是机场i和j之间的航线,而Nl为一周内该航线上的累积航班数;ki,kj分别为机场i和j的度值.如图1所示,以归一化航班密度nl作为纵轴,航线距离为横轴,蓝点即为各个航班信息在双对数坐标图中的显示.选取合适的航距范围内的点取其平均值,用红点表示,并用直线拟合红色的平均值点.从图1不难看出,无论是英国航空还是奥地利航空,归一化航班密度均随航距近似幂律衰减,可得出nl∼(rl)−0.5,表明现实航空网络的确存在时空上的关联.由于航班密度正是该航线活跃性的体现,因此可将航空网络视为一个经过高度优化设计、由预设的活跃度驱动的时变空间网络.这一时空耦合关系的发现也为网络的优化设计提供了新的方向.
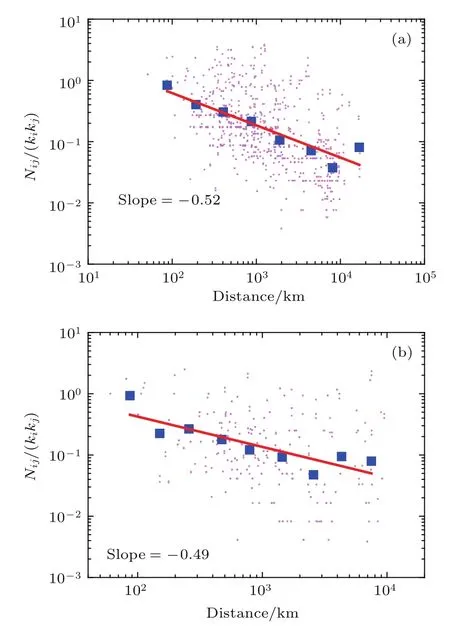
图1 航空网的时空耦合特征 (a)英国航空;(b)奥地利航空Fig.1.The coupling property between temporal and spatial factors in airline networks:(a)British airlines;(b)Austrian airlines.
3 时变空间小世界网络的优化结构
最优导航结构是空间小世界网络研究的一个重要分支,以Kleinberg为代表的学者对此进行过深入的探讨[17−23].本节运用一种活跃度驱动的时变空间小世界模型[29],讨论航空网在时变条件下的优化空间结构.N个节点分布在d维规则网格上,每个节点与其最近的2d个邻居节点相连.此外,每个节点额外拥有一条长程连边,节点i与节点j通过长边相连的概率为
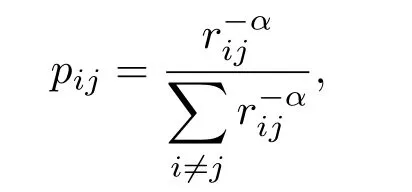
其中rij=|ri−rj|为节点间的Manhattan距离,而α为结构指数,其值越大,则长程连边的平均距离越小.此时网络中的长边分布p(r)∼r−δ,δ=α−d+1.另一方面,由上节对于航空网络时空分布特征的讨论,假设动态的连边行为是由其内在的活跃度驱动的,且每条长边lij的活跃度τij与其地理距离rij相关,满足其中参数C为连边活跃度和地理距离之间的时空耦合强度.
具体的建模及网络演化过程如下.
1)将N个节点均匀分布在一个L×L的二维周期性网格上.网络中最近邻节点间两两相连,从而保证每个节点都是可达的.
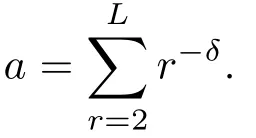
3)为每条长边赋予活跃度τij∼r−Cij.在任意时刻t,网络中的短边始终活跃,而长边以概率τ活跃,所有短边和活跃的长程连边共同构成当前时刻的瞬时网络Gt.
图2给出了上述模型的时变过程.不难看出,距离越长的连边状态转换越频繁,而距离较短的连边相对稳定,符合航空网的时变特征.在此类时变空间网络中,空间结构和连边动力学的共同作用是决定时变网络运输效率的关键.在静态网络中,大量长程连边的存在能够有效提高网络的传输效率.但在时变条件下,空间约束使得距离越长的连边其活跃的概率往往越低,从而影响网络中的传输过程.这种矛盾意味着在网络结构的设计优化中需要有效平衡时变和空间效应的影响.而网络本身也必然存在一个最优的空间结构来平衡捷径的几何长度和活跃度之间的矛盾.
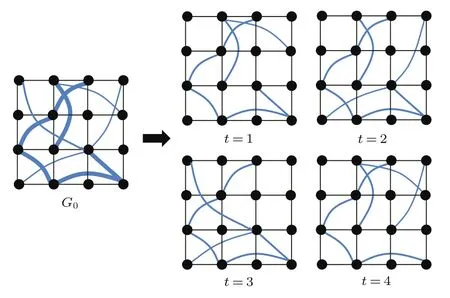
图2 时变空间小世界模型示意图(图中长程连边的粗细表示活跃度的大小)Fig.2.An illustration of the time-varying spatial small-world networks.The activity of each long-range connection is denoted by its width.
一般来说,网络的全局传输效率可以通过网络的平均最短路径长度〈l〉来衡量.而在拓扑时变的情况下,航空网络中的时变最短路径长度可以用从起点出发经过相关路径后到达目标节点所需的最短的时间来衡量.因此,当网络整体的平均时变最短路径长度〈T〉最小时所对应的空间结构就是时变条件下的优化结果.这一过程可以通过Monte Carlo方法进行模拟,由于变量α,C取值不同,平均时变最短路径〈T〉也会随之变化.对于每一个确定的耦合强度C,希望能找到使〈T〉最小的α,该α即为对应耦合强度C下的αopt.易知当C=0时,每条边的活跃度τ=1,网络即转化为Kleinberg静态网络,此时α越小,远距离的长程连边越多,所以αopt=0;当时空耦合强度0<C<2时,αopt约为2;当C≫2时,长程连边的活跃度非常小,相当于一直处于断开状态,因而αopt趋于无穷.选定C为0.5,观察随着网络规模变化αopt的变化情况,结果显示αopt稳定于2左右,因而具有很好的鲁棒性.结构指数δ与α是简单的线性关系,且通过Monte Carlo模拟发现只有当0<C<2时,该网络结构才符合小世界模型.所以结合航空网络属于小世界网络的特点,主要对处于该范围内的C和对应δopt进行分析.结果如图3所示,最优结构指数δopt随不断加深的空间约束以对数形式δopt∼log(C)缓慢增长.时空耦合强度和全局最优结构指数之间这种惟一的约束关系为时变航空网络的优化设计提供了一个崭新的方向.若确定了耦合强度C,便能快速知道最优结构指数δopt,为航空网络的航线的添加调整提供建议.

图3 全局最优结构指数δopt与时空耦合强度C的关系Fig.3.The relationship between the global optimal structural exponent δoptand temporal-spatial coupling strength C.
4 基于时变网络的航空网优化评估方法
从工程优化的角度来看,航空网络的设计是航空公司的利润和旅客的需求之间矛盾的平衡.对于航空公司而言,过高的航班频率意味着高运行成本、低客座率.而对旅客而言,航班间隔过大使得等待时间增加.因此旅客的等待成本Cp和航班的运行成本Cr是航空计划编制中需要考虑的两个主要因素[2].本节从成本最小化的角度出发,应用时变条件下最优导航结构的相关结论,提出一种航线结构的优化评估方法.
首先,假设航距为r的航线在一个周期T内航班的班次频率为f,航班的时间间隔τ=T/f.两个城市i和j之间若存在航线,则它们之间必然存在某种经济或生活上的联系,从而驱动了人们在两个城市之间的流动.一般来说,城市越发达、人口越多,则城市的吸引力越强,城市之间的人流量越大.相反,若两个城市距离非常远,考虑到出行的成本、时间等因素,人流量会相对减少.因此,两个机场之间的客流Iij通常可用引力公式的形式表征[31−36],即

其中Pi,Pj分别为两个机场所在城市的人口数;k和λ为一个常数.因此假设距离为r的航线,其客流正比于r−λ,而该航线上旅客的总等待成本取决于航班的时间间隔和客流量,即

另一方面,单个航班的运输成本一般正比于该航线的航距r,因此总的运输成本等于航班的数量与单位运输成本之积,即

因此对于航距为r的航班而言,其总体运行成本为
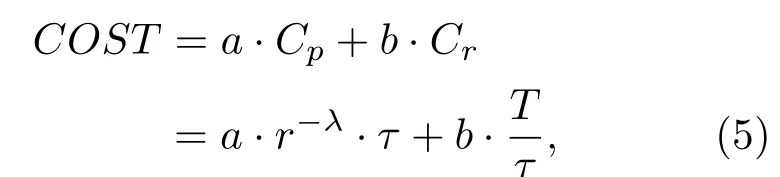
其中a,b为相关的成本系数.通过求解总成本的最小值,可以得出最佳的航班时间间隔.令dCOST/dτ=0,可以解得所以最佳航班频率满足:

考虑到实际的航空网络中航班频率与航线距离之间服从幂律耦合关系:

联立(6)和(7)式可得,时空耦合参数C与客流分布指数λ之间满足约束关系:

由(8)式和图3中给出的δopt与C的约束关系,可以确定最优的δ值,从而推得实际航线的距离分布,进而对各航空公司的航线安排是否合理做出评估.由于客流分布指数λ的值可以通过历史数据进行估计,并根据当前客流量实时调整,可以不断计算相应的C并确定最优的结构指数δ.因此评估是动态的,能反映出航空网络的发展是否在不断优化,为航空网络的结构调整提供参考.尽管这一框架经过高度简化,将所有航距为r的航班做了同质化处理,忽略了很多细节上的考虑,但是作为工程优化的前导步骤,可以为航线规划提供一些理论上的指导,而且这一方法同样适用于其他交通输运系统的整体规划.
使用中国航空网络的相关数据来对上述模型进行实证研究.首先从历年的《中国交通年鉴》中获取2001—2010十年的民航国内主要航线运输完成情况,选用其中的航班次数和客流量数据.从《中国城市年鉴》中获取了全国各大机场所在城市市辖区2001—2010年的人口数量.最后查询得到161个机场的经纬度,根据(1)式可以计算得到两两机场间的距离.
以2010年为例,将2010年国内主要航线两两城市间的客流量、各机场城市的人口数量和航线距离代入(2)式,以Iij/(pipj)为纵坐标,航距为横坐标,在双对数坐标中显示各点,计算一定航距范围内客流量平均值,拟合数据得到λ=0.4225.由C=(1+λ)/2,即可得到C=0.71125,再通过图3中C和δopt的一一对应关系就可以快速推得δopt=1.08左右.
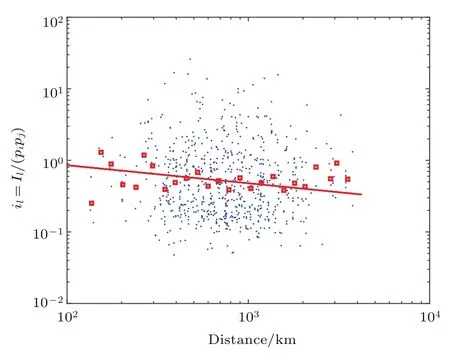
图4 2010年客流量分布与航距关系Fig.4.The relationship between the passenger fl ow and distance.
根据2010年主要航线航班频次与相应机场间的距离,按上节方法做归一化处理后,在双对数坐标中画图,同样取平均值进行拟合得到图5.由图5可以看出航班频率与航线距离呈幂律衰减,且时空耦合系数C=0.6928.
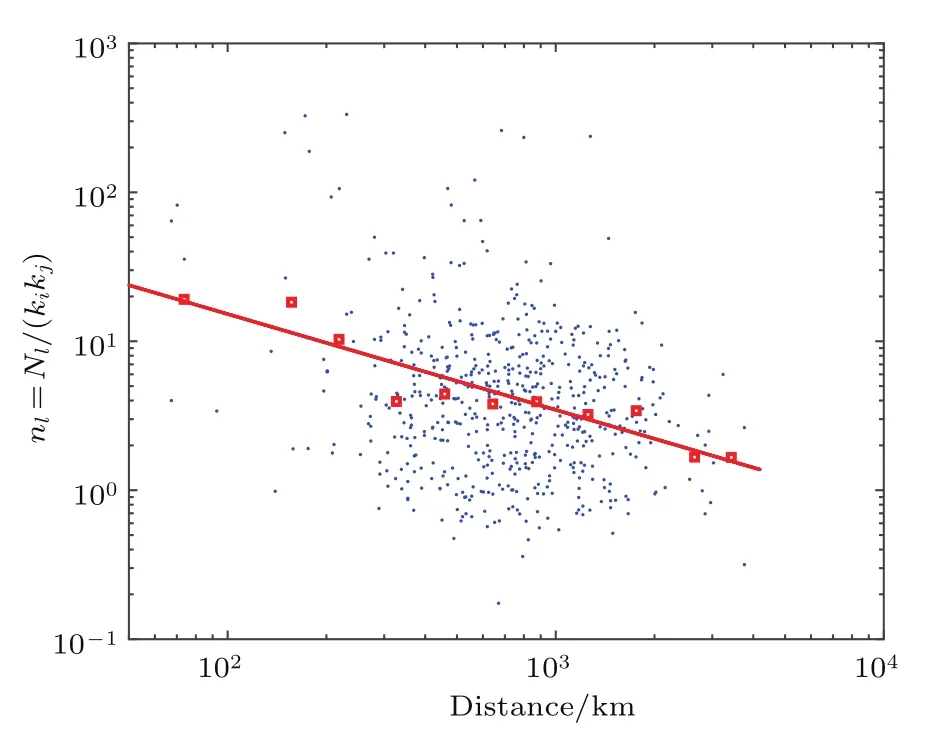
图5 2010年航班频次与航距关系Fig.5.The relationship between fl ight frequency and distance.
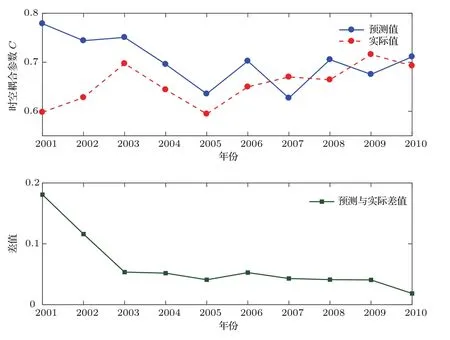
图6 2001–2010年实证数据结果分析Fig.6.The empirical results based on real data during 2001–2010.
由图4和图5可以发现由2010年客流量预测得到的时空耦合参数C与实际得到的C分别为0.71125和0.6928,相差0.01845.用同样的方法拟合2001—2009年的数据,并计算预测与实际的差值得到图6.
由于该模型主要目的是快速评估动态变化的航空网络,验证航空网络的发展是否不断优化,作为工程优化的前导步骤,因而简化了复杂的细节问题,只考虑了一些主要影响因素,比如模型推导过程中,客流量表示为基础的引力模型,影响因素只有两个城市的人口数和距离,不考虑城市经济发展情况、居民收入水平等;在航班成本最优化问题中,航班成本只由等待成本和运输成本两部分构成,其中等待成本的影响因素是客流量和航班间隔,运输成本的影响因素为航距和航班频率,忽略了机型、上座率等实际因素.所以实际数据和根据优化模型快速推算的数值存在一定的差距.但从图6可以非常直观地看到两者之间基本一致,2001年、2002年的误差相对而言较大,但随着机场建设完善,航空网络的优化,差距呈逐年递减并趋于稳定的良好趋势,从而说明该优化模型和评估方法是合理可行的.航空公司可根据客流量的变化情况来计算出C以及对应的最优结构指数,据此对现有的航线做出相应的调整,适当的增减相关航线,以实现成本降低、利润提高以及旅客满意度的提升.
5 结 论
基于空间优化网络模型和航班工程优化的思想,本文应用时变条件下最优导航结构的相关结论,提出了快速评估航线结构优化情况的方法.考虑到运输成本与航距(拓扑的空间性)密切相关,而等待成本主要取决于客座率和航班频率(拓扑的时变性)的设置,通过将最小化运行总成本作为主要的优化目标,可以推得时空耦合强度C与客流分布指数λ之间的关联.由于时变航空系统的C值还与网络的最优导航结构δopt存在惟一的约束关系,因此可以根据网络客流分布情况快速推算出航线网络的最优拓扑及相应的航班频率分布.这一思想可以避免传统优化方法求解问题的计算复杂性,能够帮助航空公司动态评估所开设航线的合理性,分析航线网络的是否在不断优化,为之后的航线增减与调整提供建议.
[1]Brueckner J K 2004J.Ind.Econ.52 291
[2]Li F J,Wang L P,Liu Z Y 2007Comput.Eng.33 279(in Chinese)[李福娟,王鲁平,刘仲英2007计算机工程33 279]
[3]Zheng X,Yu T 2014IEEE Workshop on Advanced ResearchandTechnologyinIndustryApplications(WARTIA)Ottawa,Canada,September 29–30,2014 pp1135–1137
[4]Dobson G,Lederer P J 1993Transp.Sci.27 281
[5]Wang W,Wang C J 2013Acta Geogr.Sin.68 762(in Chinese)[王伟,王成金 2013地理学报68 762]
[6]Gautreau A,Barrat A,Barthelemy M 2009Proc.Natl.Acad.Sci.USA106 8847
[7]Qian J H,Han D D,Ma Y G 2011Acta Phys.Sin.60 098901(in Chinese)[钱江海,韩定定,马余刚2011物理学报60 098901]
[8]Han D D,Qian J H,Liu J G 2009Physica A388 71
[9]Barrat A,Barthelemy M,Pastor-Satorras R,Vespignani A 2004Proc.Natl.Acad.Sci.USA101 3747
[10]Guimera R,Mossa S,Turtschi A,Amaral L A N 2005Proc.Natl.Acad.Sci.USA102 7794
[11]Liu H K,Zhou T 2007Acta Phys.Sin.56 106(in Chinese)[刘宏鲲,周涛 2007物理学报 56 106]
[12]Luo Y Q,Tang J H,Zhao Z L,Zhu Y W,Dong X J 2014Complex Systems and Complexity Science11 4(in Chinese)[罗赟骞,汤锦辉,赵钟磊,朱永文,董相均2014复杂系统与复杂性科学11 4]
[13]Lordan O,Sallan J M,Simo P 2014J.Transp.Geogr.37 112
[14]Moukarzel C F,de Menezes M A 2002Phys.Rev.E65 056709
[15]Kosmidis K,Havlin S,Bunde A 2008Europhys.Lett.82 48005
[16]Yang H,Nie Y C,Zeng A,Fan Y,Hu Y Q,Di Z R 2010Europhys.Lett.89 58002
[17]Kleinberg J M 2000Nature406 845
[18]Kleinberg J M 2000Proceedings of the Thirty-Second Annual ACM Symposium on Theory of ComputingPortland,USA,May 21–23,2000 pp163–170
[19]Boguna M,Krioukov D,Claffy K C 2009Nat.Phys.5 74
[20]Pajevic S,Plenz D 2011Nat.Phys.8 1
[21]Milo R,Shenorr S,Itzkovitz S,Kashtan N,Chklovskii D,Alon U 2002Science298 824
[22]Li G,Reis S,Moreira A,Havlin S,Stanley H E,Andrade Jr J 2013Phys.Rev.E87 042810
[23]Li Y,Dou F L,Fan Y,Di Z R 2012Acta Phys.Sin.61 228902(in Chinese)[黎勇,钭斐玲,樊瑛,狄增如 2012物理学报61 228902]
[24]Gastner M T,Newman M 2006Phys.Rev.E74 016117
[25]Holme P,Saramäki J 2012Phys.Rep.519 97
[26]Kim H,Anderson R 2012Phys.Rev.E85 026107
[27]Starnini M,Baronchelli A,Barrat A,Pastor-Satorras R 2012Phys.Rev.E85 056115
[28]Trajanovski S,Scellato S,Leontiadis I 2012Phys.Rev.E85 066105
[29]Chen Q,Qian J H,Zhu L,Han D D 2016Phys.Rev.E93 032219
[30]Chen Q,Qian J H,Zhu L,Han D D 2016J.Appl.Anal.Comput.6 30
[31]Wojahn O W 2001Transport Res.E37 267
[32]Grosche T,Rothlauf F,Heinzl A 2007J.Air Transp.Manag.13 175
[33]Qian J H,Han D D 2009Physica A388 4248
[34]Jung W S,Wang F,Stanley H E 2008Europhys.Lett.81 48005
[35]Qian J H,Han D D 2009Acta Phys.Sin.58 3028(in Chinese)[钱江海,韩定定 2009物理学报 58 3028]
[36]Nõmmik A,Kukemelk S 2016Aviation20 32
