有机电光晶体4-(4-二甲基氨基苯乙烯基)甲基吡啶对甲基苯磺酸盐的太赫兹光谱研究∗
2018-01-18连宇翔戴泽林许向东谷雨李欣荣王福杨春成晓梦周华新
连宇翔 戴泽林 许向东 谷雨 李欣荣 王福杨春 成晓梦 周华新
1)(电子科技大学光电信息学院,电子薄膜与集成器件国家重点实验室,成都 610054)2)(四川师范大学化学与材料科学学院,成都 610068)
(2017年6月28日收到;2017年7月25日收到修改稿)
1 引 言
太赫兹(THz)波是指频率从0.1—10 THz的电磁波,介于毫米波与远红外之间(3 mm—30µm).THz波具有良好的介质穿透性、低电离能和相干性等优异特性.而且,许多大分子化合物的特征谱也在THz频段,因此THz技术在物理、化学、生物、天文和医药科学等基础研究领域以及医学成像、环境监测、安全检查等应用研究领域均具有巨大的科研价值和广阔的应用前景[1].近年来,利用有机电光晶体的光整流效应进行太赫兹波的产生和探测已成为太赫兹光子学领域重要的研究课题.与传统的无机电光晶体相比,性能优良的有机电光晶体更易设计和合成.为了满足太赫兹源和太赫兹探测的需要,大量具有较高的二阶非线性系数的新的有机电光晶体已相继被合成出来,其中最具代表性的是一种有机吡啶磺酸盐,即4-(4-二甲基氨基苯乙烯基)甲基吡啶对甲基苯磺酸盐(DAST).Zhang等[2]开展的DAST的光整流产生太赫兹辐射的实验表明,DAST的整流电场强度是无机电光晶体LiTaO3的185倍、GaAs和InP晶体的42倍.这主要得益于DAST较高的二阶非线性系数(在1318 nm波长激光作用下,DAST的二阶非线性系数d111=(1010±110)pm/V)和电光系数(在1535 nm波长激光作用下,DAST的电光系数r111=(47±8)pm/V)[3].然而,DAST在太赫兹波段还表现出强烈的吸收和色散[4,5],这对获得连续宽带的太赫兹光源极为不利.强烈的吸收带会严重地降低太赫兹产生效率,而强烈色散也会使得相位匹配不容易实现.类似的情况也在其他有机电光分子晶体如PNP,OH1[6]中出现.因此,研究有机电光晶体在太赫兹波段的吸收和色散性质,对于理解其太赫兹波产生和探测的特点以及优化和设计高效的用于太赫兹源和探测的新材料等,具有重要的意义.
Walther等[4]对DAST单晶在0—3 THz波段a轴和b轴的吸收和折射率色散性质进行了系统的测量,结合简单的横向光学声子计算,认为DAST在此波段的振动主要是源于阴阳离子间的光学声子振动.然而,Walther等并未对这些吸收峰对应的振动方式进行具体的归属和验证.Glavcheva等[5]测试了DAST粉末在0.63—10.6 THz的吸收光谱,但缺乏深入的分析.显然,详细的模式分析不仅有助于理解声子振动的起源,为今后合成性能更优的新的DAST衍生物以及其他有机电光晶体提供有价值的指导,同时也有助于理解DAST作为太赫兹发射和探测的特点及注意环节.遗憾的是,到目前为止,此项研究在国内外文献中十分罕见.虽然Saito等[7]使用第一性原理对DAST进行了理论计算,然而其计算结果与实验测量的结果出入较大,这可能是由于计算参数和初始结构不合理.而且,作者仅对103.2 cm−1处的吸收峰做了模式分析[7],缺乏对低频的声子振动进行详细的讨论.
详细地分析和归属太赫兹振动谱带有利于更加深入地了解低频振动动力学的物理机理,这一任务可通过基于密度泛函理论(DFT)的量子力学计算实现.传统的中红外光谱振动模式主要取决于分子内的共价键作用.与之不同,太赫兹光谱与分子间的相互作用,例如氢键和范德瓦耳斯力密切相关.因此,理论计算的一个关键问题是如何合理地描述这些非共价键作用.最近,我们通过对简单磺酸类有机物牛磺酸进行DFT光谱分析发现[8],对于氢键分子晶体,色散校正在模拟分子在晶体中所处的环境时十分重要[9,10].与简单的牛磺酸小分子相比较,DAST的分子量更大、结构更加复杂,因此需要通过引入色散校正的方法对DAST进行结构优化及太赫兹光谱计算.为此,本文首次采用周期性固态色散校正的密度泛函理论(dispersion-corrected density functional theory,DFT-D2),对有机电光晶体DAST在0—4 THz的声子振动模式进行详细的分析和归属.在收敛测试的基础上,使用逐步提高收敛精度优化法进行红外光谱计算.根据DFT计算结果,探究DAST主要振动模式的起源.本文不仅探索出使用一个从头算量子力学程序Cambridge sequential total energy package(CASTEP)预测复杂分子红外光谱的合适方法,还揭示了DFT计算在太赫兹光子学中的重要应用价值.对探究有机电光晶体的太赫兹响应物理原理具有重要的指导价值.
2 理论计算
2.1 DFT计算
DFT是用来研究多电子体系电子结构的一种量子力学的方法,在物理、化学、材料等领域都有广泛应用.研究表明单个分子的DFT计算,不能很好地模拟范德瓦耳斯力在分子间的作用,导致模拟计算结果与实验有一定差别[11,12].为了解决这一问题,采用Grimme[13]的方法将范德瓦耳斯作用中的色散力校正项引入到DFT计算中(DFT-D2法)[8].在该方法中,体系中各原子对之间的范德瓦耳斯相互作用通过一个简单的成对力场来描述.本文使用CASTEP对有机电光晶体DAST进行结构优化和太赫兹光谱计算.与液相或气相的独立分子建模计算相比较,CASTEP考虑了固体的周期性晶格排布,更为准确地描述了分子吸收光谱以及集体振动模式.同时,在太赫兹波段的分子振动模式识别中,尤其是研究分子间或分子内作用力时,周期性DFT计算已经被广泛采用[14,15].据此,本文采用周期性固态DFT-D2方法进行DAST的太赫兹光谱计算.
2.2 计算参数设置及优化
选取Marder等建立的DAST晶格参数和原子坐标作为计算的初始结构[16].在几何优化之前,分别对截断能和k点网格进行测试,以便选取合适的计算参数用于结构优化和光谱计算.所有周期性DFT计算均在CASTEP[17]上完成.优化后的平面波截断能设为800 eV,选用广义梯度[18]近似下的Perdew-Burke-Ernzerhof(PBE)泛函作为交换关联函数的近似.几何优化和光谱计算均采用模守恒赝势和Monkhorst-Packk点网格(5×5×5).使用Grimme的PBE-D2方法[19]将色散校正项引入PBE泛函.该方法中库仑作用通过成对的力场加以描述.在PBE-D2方法的计算中,晶格常数和原子坐标均完全弛豫.几何优化的总能量收敛标准均设为10−6Hartree.计算得到的光谱采用5 cm−1半高全宽的洛伦兹线型绘制.
3 结果与讨论
有机电光晶体DAST作为太赫兹发射源,主要利用其较高的二阶非线性系数.DAST分子由一个带正电的有机吡啶盐和一个带负电的磺酸盐组成,如图1(a)所示.其中,有机吡啶盐由电子给体(二甲基氨基)、共轭π桥(苯乙烯基)和电子受体(甲基吡啶)组成.带正电荷的甲基吡啶具有很强的吸电子能力,并与二甲基氨基通过苯乙烯基形成推-拉电子结构,因此该结构具有很大的一阶超极化率.DAST的有机吡啶盐链可看作一个偶极子(如图1(a)所示),其极化率p可表示为
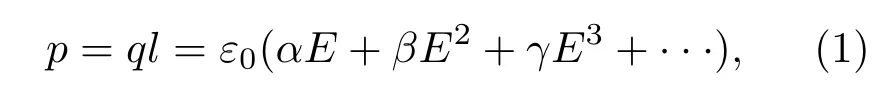
其中,q为电荷电量,l为电荷间位移矢量,ε0为真空介电常数,E为外加电场;α,β和γ分别为分子的一阶、二阶和三阶非线性系数.在DAST晶体中,磺酸盐(负)与有机吡啶盐(正)电荷间的库仑作用大于有机吡啶盐间的偶极子-偶极子作用,使得有机吡啶盐沿着与a轴夹角约为20°的方向排列(如图1(d)所示).而且,整个DAST在三维空间中以非中心对称的形式排列,以获得最大的宏观极化率.宏观极化率P可表示为

其中,χ(1),χ(2)和χ(3)分别为一阶、二阶和三阶非线性系数.χ(2)与β成正比关系[20],即分子的超极化率越大,晶体的二阶非线性系数越大.

图1 (网刊彩色)DAST分子结构及其原胞沿各轴方向上的分子排列 (a)DAST的分子结构(由右侧一个带正电的有机吡啶盐和左侧一个带负电的磺酸盐组成);(b)DAST原胞沿a轴(晶格夹角A)的分子排列;(c)DAST原胞沿b轴(晶格夹角B)的分子排列;(d)DAST原胞沿c轴(晶格夹角Γ)的分子排列Fig.1.(color online)DAST molecular structure and the molecular arrangement of the cells along the axis:(a)DAST molecular structure consisting of a positively-charged organic pyridine salt and a negatively-charged sulfonate;(b)the molecular arrangement of the cells along a axis(lattice angle A);(c)the molecular arrangement of the cells along b axis(lattice angle B);(d)the molecular arrangement of the cells along c axis(lattice angle Γ).
从以上讨论可以看出,DAST之所以具有非常高的二阶非线性系数,主要是源于有机吡啶盐较大的分子极化率及其非中心对称的分子排列方式.磺酸盐的存在主要是为了使有机吡啶盐能够在晶体内有序地定向排列.这种成盐的方式是设计和合成二阶非线性材料的重要方法[16].阴阳离子间的库仑作用为DAST稳定的非中心对称结构提供了保障.虽然DAST极高的二阶非线性系数使得其通过光整流技术在太赫兹源的应用上具有优势,但是DAST的这种结构也使其在太赫兹波段存在本征吸收带,影响太赫兹波发射效率.下面重点分析DAST在太赫兹波段强的声子吸收带的起源.
在进行几何优化时,发现直接对初始结构进行高精度计算得到的最终结构与实验值差别较大(优化后的晶格常数与实验值相差超过10%),这可能是由于实验所测的DAST初始结构不太合理,与基态相差较大.为此,本文采用逐步增加收敛精度的方法.首先,进行低精度的计算,然后逐步过渡到高精度.图2显示了从低精度到高精度(分别对应CASTEP几何优化中的coarse,medium, fi ne和ultra fi ne)优化过程中晶格常数a,b,c和晶格夹角A,B,Γ(图2)的变化.
从图2可以看出,在逐步提高收敛精度优化过程中,晶格常数、晶格夹角与实验值相比波动很小(小于1%),而且优化过程中晶格对称性保持不变,晶格常数始终保持a=b,晶格夹角A=B.这表明,逐步优化的方法是可行的.为了方便比较,表1列出了ultra fi ne后的晶格常数与晶格夹角同初始结构实验数据的对比.图2中,随着收敛精度的提高,晶格常数a,b,c的变化较小(Δa= Δb=0.0095 Å,0.0012%;Δc=0.1154 Å,0.0065%);晶格夹角A,B,Γ虽然在medium和 fi ne相对初始结构出现了超过1°的变化,但是最终的夹角参数(ultra fi ne)与初始实测结构相比,变化也很小(ΔA= ΔB=05012°,0.0055%;ΔΓ=0.089°,0.0009%).几何优化本质上是寻找体系的最小能量状态,低精度的优化有助于将优化的方向逐步推向正确的收敛方向.逐步优化的方法对于大体系的结构优化十分有效,既能节省时间和计算成本,又能找到体系的基态.优化结果表明,采用逐步收敛的方法,能够较好地得到DAST的基态稳定结构,使得理论计算得到的太赫兹光谱与实测结果更好地相符.
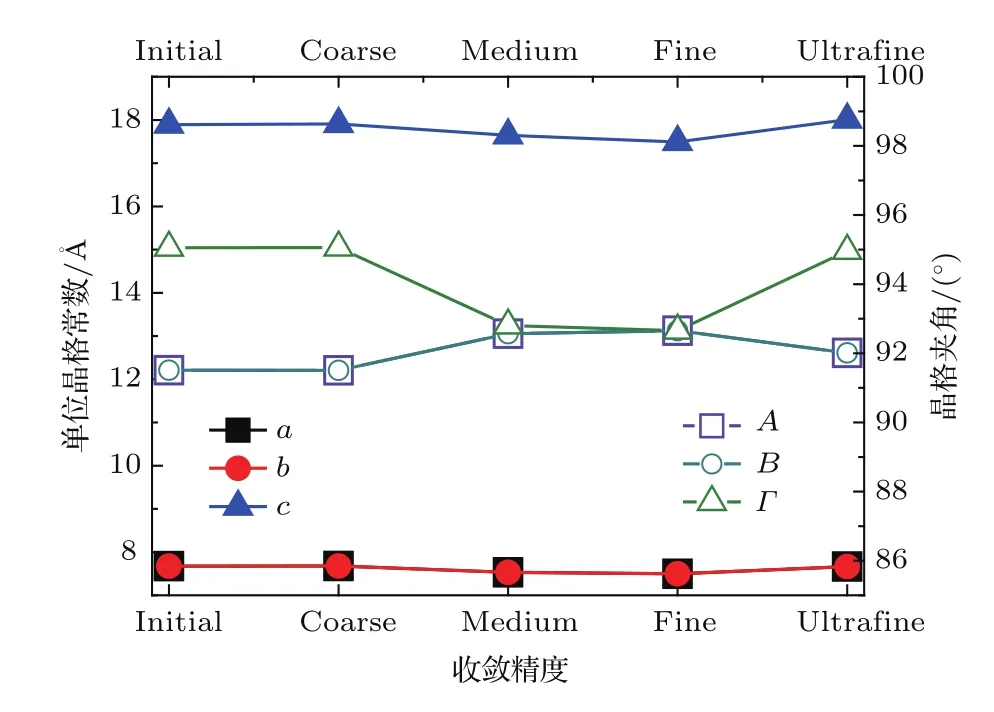
图2 (网刊彩色)逐步优化过程中DAST晶格参数变化(晶格常数a,b,c;晶格夹角A,B,Γ;对应收敛精度从低精度initial到高精度ultra fi ne)Fig.2.(color online)Changes of the DAST lattice parameters during gradual optimization(lattice constants of a,b and c;lattice angles of A,B and Γ;convergence accuracy from initial to ultra fi ne).

表1 DAST初始结构实验数据同结构收敛优化后对比(晶格常数a,b,c;晶格夹角A,B,Γ)Table 1.Comparison of the experimental data for the initial structure of DAST and those obtained by structure optimization(lattice constants of a,b and c;lattice angles of A,B and Γ).
最近,我们采用DFT-D2方法,对牛磺酸小分子的太赫兹光谱进行计算,得到与实验较为相符的仿真结果[8].据此,本文采用DFT-D2方法,对复杂程度更高、分子量更大的DAST在0—4 THz波段的太赫兹光谱进行了计算,结果如图3所示.作为比较,图3还给出了Glavcheva等[5]的DAST多晶粉末的太赫兹光谱测量结果.图3显示,DFT计算很好地重现了实测的5个吸收峰M1—M5的位置,这为进一步分析DAST在这一波段的振动起源奠定了基础.注意到虽然Saito等[7]基于第一性原理的光谱计算也重现出了M1和M5,与本文的计算结果类似.但是,Saito等[7]的计算没有很好地重现M2,M3,M4三个振动模式,而且其计算得到的峰形与实验结果差别较大.与之不同,本文对M1—M5振动模式都很好地进行了重现.据我们所知,本文是第一次通过DFT理论计算的方法完全预测出DAST在0—4 THz范围的所有振动模式.而且,在本文仿真过程中,红外光谱计算没有虚频产生,说明采用逐步优化的方法得到的基态结构是稳定的.同时说明采用DFT-D2方法,仿真获得的DAST的太赫兹光谱与实测数据的符合程度高,说明色散校正的引入确实可以较好地模拟分子在晶体中的环境.

图3 (网刊彩色)在0—4 THz波段,通过DFT仿真计算的DAST太赫兹光谱与实验测量的DAST粉末太赫兹光谱(文献[5])的比较Fig.3.(color online)Comparison of the DAST THz spectrum in the frequency band of 0–4 THz simulated by DFT and that for the DAST powder experimentally measured(Ref.[5])
为便于比较,表2列出了理论计算和实测吸收峰的位置,它们之间的平均误差仅为0.088 THz(约2.9 cm−1).值得注意的是,M1和M3两个较强的吸收带也在以往DAST单晶偏振测试中出现[5],是DAST在太赫兹低频波段的主要吸收峰.

表2 IR计算的频率位置与实测结果的比较Table 2.Comparison of the frequency positions obtained by IR calculation and the experimentallymeasured results.
为了探究DAST的物理特性,本文继续对DAST在太赫兹波段的声子模式归属进行研究.图4显示了振动模式M1—M5的振动位移矢量图.下面结合CASTEP的动画模拟功能,讨论DAST实测的太赫兹吸收峰的起源.单分子振转模式表现分子内各基团的振动和转动,而晶胞分子的振转模式则比较复杂,表现为晶胞各分子的对称和非对称弯曲的协同振动以及分子内基团振动.在1.12 THz(对应计算的M1)处,DAST阳离子(有机吡啶盐)和阴离子(磺酸盐)分别在各自的(苯环)平面内发生平移振动.阴阳离子的振动方向如图中红色箭头所示.该模式可归属为阴阳离子的相对运动,即光学声子模式.从图4可以看出,阴阳离子的相对振动方向基本沿着a轴,这解释了当使用沿着a轴偏振的太赫兹入射波进行光谱测试时,DAST单晶在M1处的吸收峰强度高于沿b轴偏振测试的吸收强度的现象[4].1.46 THz(对应计算的M2)和1.54 THz(对应计算的M3)主要源于有机磺酸盐的振动.其中,1.46 THz的振动是由于磺酸盐沿a轴的转动,而1.54 THz则是由于整个磺酸离子沿着c轴的平动.这两处的吸收峰与阳离子基本无关.在文献[5]中,Glavcheva等[5]还比较测量了DAST和DASC的太赫兹光谱.DASC的结晶类型和化学结构与DAST相似,不同之处是磺酸盐上的—CH3被—Cl取代.Glavcheva等[5]的实测结果显示,两者的低频振动模式M1—M5位置完全相同.这暗示着DAST的振动模式M1—M5与单个—CH3官能团无关,而更有可能与阴阳离子间的集体振动有关.这不仅体现了太赫兹振动模式本质上的复杂性,也有助于人们更加直观地认识到中红外光谱与太赫兹光谱的不同:中红外光谱对于物质的化学成分(化学键)更加敏感,而太赫兹光谱则对于物质的结构排列更为敏感.由于有机电光晶体DAST二阶非线性的贡献主要来源于有机吡啶盐阳离子大的分子极化率及其非中心对称的分子排列,这为设计具有二阶非线性的有机电光晶体DAST新型衍生物提供了一个方向,即通过设计或改变阴离子基团来消除DAST在1.46 THz(对应计算的M2)和1.54 THz(对应计算的M3)处的吸收,从而有望提高太赫兹波的产生效率.仔细观察还发现,M2和M3的振动中阴离子的苯环振动较强,因此可以通过改变阴离子的结构,例如将苯环替代成烷烃或其他官能团,或将苯环的H原子用其他官能团取代,牵制苯环的振动,据此达到减弱或消除M2和M3处吸收的目的.反之,如果需要利用DAST在太赫兹波段的吸收特性,则可以考虑通过取代阴阳离子基团来增强DAST在太赫兹波段的吸收.2.63 THz(对应M4)处主要是有机吡啶盐两个苯环的扭转振动以及阴离子绕a轴的转动.而3.16 THz处最强的吸收峰(对应M5)与M4的振动类型类似,但振动的方向不同(如图中红色箭头所指示).综合这几处的振动模式可以发现,有机磺酸盐阴离子在DAST的低频振动中起了关键的作用.本文首次对DAST在0—4 THz范围太赫兹光谱的特征峰进行了系统归属.
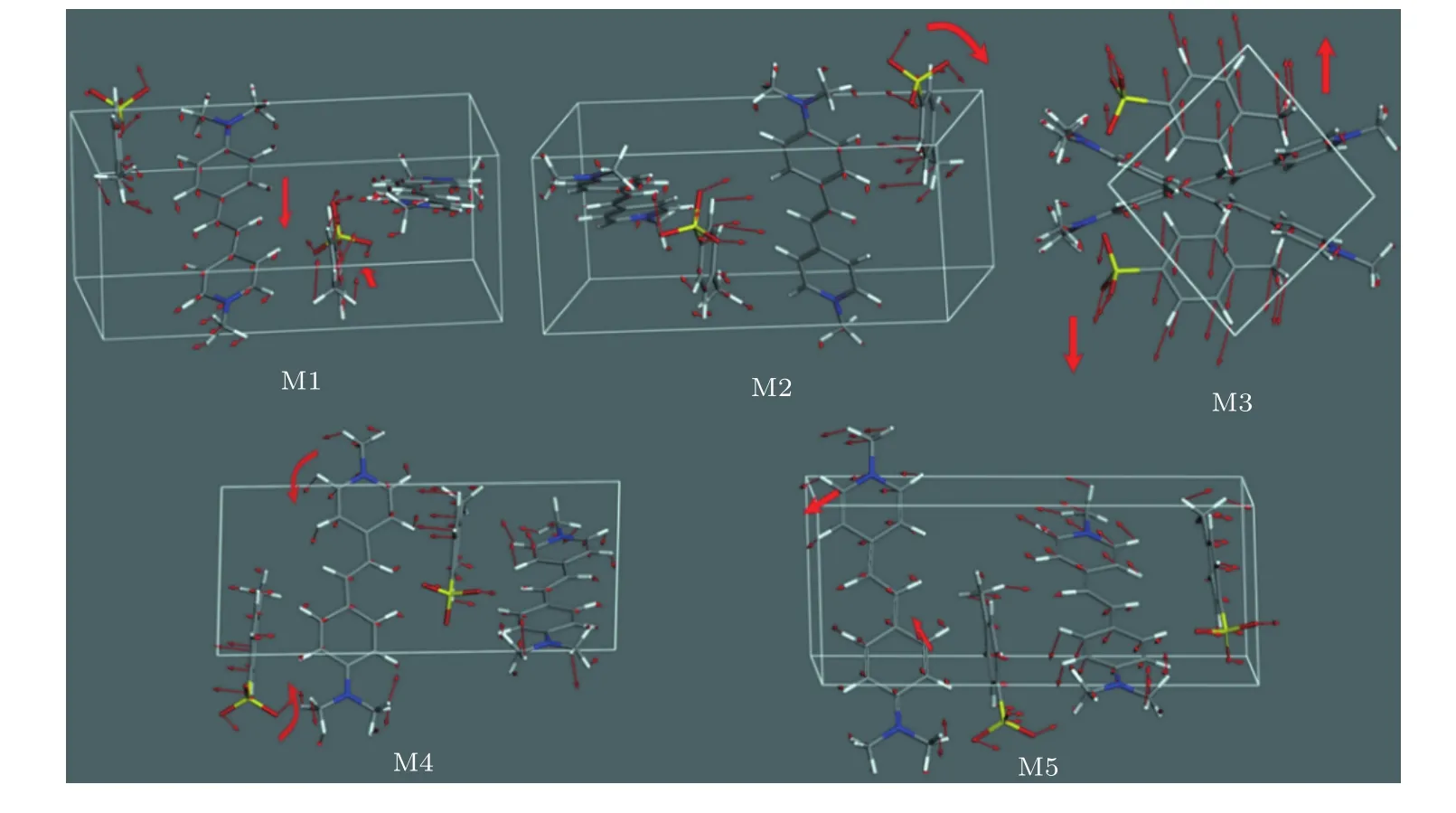
图4 (网刊彩色)通过CASTEP动画模拟功能得到的DAST分子振动模式M1—M5对应的振动位移矢量图,其中,M1源于阳离子(有机吡啶盐)、阴离子(磺酸盐)分别在各自的(苯环)平面内发生平移振动;M2,M3分别源于阴离子沿a轴、c轴转动;M4源于阳离子两个苯环扭转振动、阴离子绕a轴的转动;M5源于阴阳离子苯环扭转转动Fig.4.(color online)Vibration displacement vector diagrams for the DAST molecular structure obtained by CASTEP animation simulation function.M1 is originated from the DAST cation(organic pyridinium salt)and anion(sulfonate)undergo translational vibrations in their respective(benzene ring)plane;M2 and M3 are assigned to the anion rotates along the a axis and c axis,respectively;M4 is related to the torsional vibrations of two benzene rings on cation and the anion rotates around the a axis;M5 is attributed to the torsional vibrations of the benzene rings in the cation and anion.
4 结 论
首次将DFT-D2用于计算结构复杂的有机磺酸盐DAST的太赫兹光谱.在收敛测试(k点和截断能测试)的基础上,采用逐步提高精度进行几何优化的方法寻找DAST收敛的基态稳定结构.结果表明,该方法不仅很好地重现了DAST的结构参数(例如晶格常数和夹角),而且在此结构基础上计算的太赫兹光谱与实测光谱较好地相符.在此基础上,首次对DAST在0—4 THz范围太赫兹光谱的特征峰进行系统归属.模式分析结果表明,1.12 THz处的振动是DAST的阴阳离子的光学声子模式,1.46 THz和1.54 THz两处的振动主要与其磺酸盐相关,而2.63 THz和3.16 THz两处的振动则源于阳离子的扭转振动和阴离子的转动.这说明在不改变DAST二阶非线性效应的基础上,能够通过设计、改变磺酸盐阴阳离子基团的方式,减弱DAST在太赫兹波段的吸收,提高材料在太赫兹波段的发射效率.研究有机电光晶体DAST在太赫兹波段的振动模式归属不仅有助于全面掌握DAST在太赫兹的吸收特性,对研制性能更加优越的新型太赫兹有机敏感材料,探索DAST基材料在太赫兹探测器中的新应用等都具有重要的意义,还为今后合成具有更优二阶非线性的DAST新型衍生物提供了重要的参考和指导.本文结果揭示了DFT在太赫兹光子学中的重要应用价值,为使用DFT计算预测其他用于有机电光晶体的太赫兹吸收性能提供了可资的借鉴方法,有助于深入探究有机电光晶体的太赫兹响应的物理原理.
[1]Ferguson B,Zhang X C 2002Nat.Mater.1 26
[2]Zhang X C,Ma F,Jin Y,Lu T M,Boden E P,Phelps P D,Stewart K R,Yakymyshyn C P 1992Appl.Phys.Lett.61 3080
[3]Bosshard C,Spreiter R,Degiorgi L,Gunter P 2002Phys.Rev.B66 205107
[4]Walther M,Jensby K,Keiding S R 2000Opt.Lett.25 911
[5]Glavcheva Z,Umezawa H,Mineno Y,Odani T,Okada S,Ikeda S,Taniuchi T,Nakanish H 2005Jpn.J.Appl.Phys.44 5231
[6]Kim J,Kwon O P,Brunner F D J,Jazbinsek M,Lee S H 2015J.Phys.Chem.C119 10031
[7]Saito S,Inerbaev T M,Mizuseki H,Igarashi N,Note R,Kawazoe Y 2006Chem.Phys.Lett.432 157
[8]Dai Z L,Xu X D,Gu Y,Li X R,Wang F,Lian Y X,Fan K,Chen X M,Chen Z G,Sun M H,Jiang Y D,Yang C,Xu J 2017J.Chem.Phys.146 124119
[9]Kim J,Kwon O P,Jazbinsek M,Park Y C,Lee Y S 2015J.Phys.Chem.C119 12598
[10]King M D,Buchanan W D,Korter T M 2011Phys.Chem.Chem.Phys.13 4250
[11]Takahashi M 2014Crystals4 74
[12]Grimme S,Ehrlich S,Goerigk L 2011J.Comput.Chem.32 1456
[13]Grimme S 2004J.Comput.Chem.25 1463
[14]Miles R E,Zhang X C,Eisele H,Krotkus A 2007Terahertz Frequency Detection and Identi fi cation of Materials and Objects(Netherlands:Springer)pp147–163
[15]Zhang Y,Peng X H,Chen Y,Chen J,Curioni A,Andreoni W,Nayak S K,Zhang X C 2008Chem.Phys.Lett452 59
[16]Seidler T,Stadnicka K,Champagne B 2014J.Chem.Phys.141 104109
[17]Clark S J,Segall M D,Pickard C J,Hasnip P J,Probert M I J,Refson K,Payne M C 2005Zeitschrift für Kristallographie220 567
[18]Perdew J P,Burke K,Ernzerhof M 1996Phys.Rev.Lett.77 3865
[19]Grimme S 2006J.Comput.Chem.27 1787
[20]Marder S R,Perry J W,Yakymyshyn C P 1994Chem.Mater.6 1137
