例谈函数导数压轴题的解题突破策略

2018-01-18广东省佛山市第一中学528000吴统胜

中学数学研究(广东) 2017年23期

广东省佛山市第一中学(528000) 吴统胜

考生对函数导数压轴题是有恐惧心理的,思维强度大,题型多,方法性强而灵活,解题突破口不易找寻,常需适当变形转化证明,对数学能力的要求相当高,肩负名牌学校的选拔重任!但压轴题还是有其规律性的,只要我们充分利用好导数这个工具,做好题型的归类和方法总结,掌握好通性通法,如构造函数法、常见函数型不等式放缩法、主元法、分离变量法等方法,加强对转化与化归、数形结合、函数方程、分类讨论等数学思想方法的渗透,辅之以一定量的强化训练,有助于学生快速找寻解题思路和方法,克服对压轴题的恐惧心理,尖子生利用函数导数压轴题得高分也是可能的,更是必然的!

笔者在[1-2]两篇文章中,对函数型不等式压轴题的证明方法进行了较详细的探究、优化、拓展推广,总结了该类函数型不等式压轴题的一般化、“套路化”的解法.本文笔者结合高考题对函数导数压轴题的解题突破策略做了更深入、更详尽的总结提升.下面举例说明函数导数压轴题的几种解题突破策略!

一.解题突破策略

解题突破策略一直接构造函数法

例1(2013年课标II理科21)已知函数f(x)=ex−ln(x+m).

(1)设x=0是f(x)的极值点,求m,并讨论f(x)的单调性;

(2)当m≤2时,证明:f(x)＞0.

解析(1)略;

(2)当m≤2时,

构造函数φ(x)=ex−ln(x+2),转化为求证φ(x)min=φ(x0)＞0,但使对应的x0不易求出,需利用零点存在定理及设而不求法求得最小值,只要证明φ(x)min=φ(x0)＞0.其证明过程如下:

当m≤2时,

设φ(x)=ex−ln(x+2),则在(−2,+∞)上单调递增.又φ′(−1)＜0,φ′(0)＞0,所以φ′(x)=0 在(−2,+∞)上有唯一实根,且x0∈(−1,0).当x∈(−2,x0)时,φ′(x)＜0;当x∈(x0,+∞)时,φ′(x)＞0.所以φ(x)min=φ(x0).由φ′(x0)=0得:

解题突破策略二转化证明法

若直接构造函数证明较困难,可对不等式两边适当变形,转化为两个函数的最大值与最小值的大小比较问题,再利用构造函数法证明!

例2(2017年佛山二模理科21)设函数f(x)=aex−xlnx,其中a∈R,e是自然对数的底数.

(1)若函数f(x)是(0,+∞)上的增函数,求实数a的取值范围;

解析(1)略;

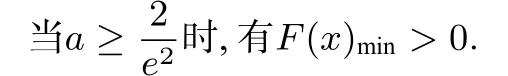
对要证不等式进行适当变形,转化证明:

φ(x)min＞h(x)max.所以原不等式得证!

此法相当巧妙,证明过程较为简洁!

例3(2017年广州一模理科21)已知函数.

(1)若函数f(x)有零点,求实数a的取值范围;

解析(1)(略).

这类同时含有ex,lnx的不等式常采用该转化证明的方法.

该题改编自2014年全国I理科第21题:

(I)求a,b;

(II)证明:f(x)＞1.

而2014年全国I理科第21题改编自2014年黑龙江高中数学预赛题,其题目如下.

证明:对一切x∈(0,+∞)都有成立.

解题突破策略三巧用常见函数型不等式

常见函数型不等式主要有以下三种类型:

1.函数型不等式类型1的运用

(见人教版教材《选修2-2》P32习题1.3B组第1题)(可结合图一加深学生对不等式的理解记忆)

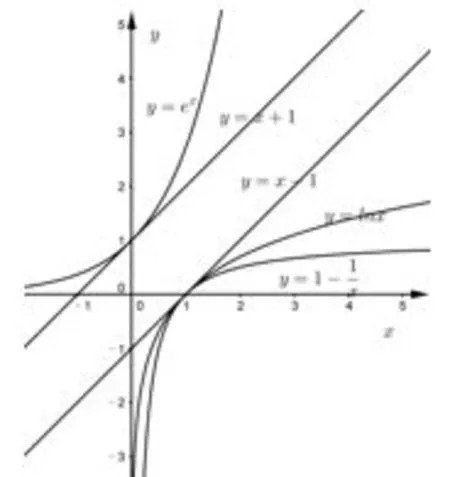
图1

题目同例1.

解析在例1中我们采用策略一,直接构造函数φ(x)=ex−ln(x+2),转化为求证φ(x)min=φ(x0)＞0,但使对应的x0不易求出,需利用零点存在定理及设而不求法求得最小值,并证明φ(x)min=φ(x0)＞0,证明过程稍显复杂,对数学思维和能力要求较高.但若妙用函数型不等式:ex≥x+1及lnx≤x−1(x＞0),则证明过程相当简便,其证明过程如下:

证明因为lnx≤x−1(x＞0),所以

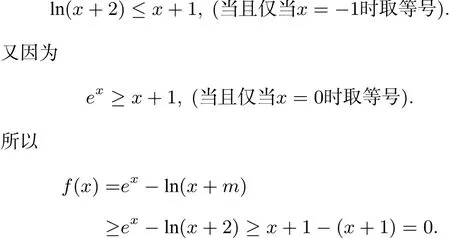
因为两等号不同时取得,所以当m≤2时,f(x)＞0.

2.函数型不等式2的运用

证明设,所以

当 0＜x＜e时,h′(x)＞0,h(x)递增;当x＞e时,h′(x)＜0,h(x)递减;所以h(x)max=h(e)=0,所以h(x)≤h(x)max=0,所以.

题目同例2.

解析(1)略;

3.函数型不等式3的运用

例4(2013陕西理科21题)已知函数f(x)=ex,x∈R.

(1)若直线y=kx+1与f(x)的反函数的图像相切,求实数k的值;

(2)设x＞0,讨论曲线y=f(x)与曲线y=mx2(m＞0)公共点的个数.

(3)设a＜b,比较的大小,并说明理由.

突破策略四对于二元(或多元)不等式类型,多采用二元(或多元)化一元,再恰当构造函数证明不等式.

例5已知函数f(x)=lnx(x＞0),设b＞a＞0,求证:.

点评对于二元(或多元)不等式类型,多采用二元(或多元)化一元,再恰当构造函数证明不等式.该不等式的变式:

突破策略五处理二元(多元)不等式的另外一种行之有效的方法—主元法

例6同例4.

解析(1)(2)略;

(3)证明:因为a＜b,所以b−a＞0,所以比较

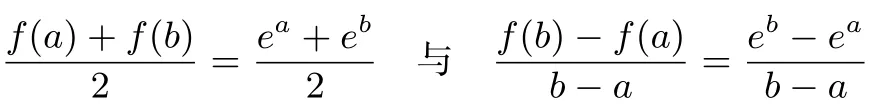
的大小,即比较(b−a)(ea+eb)较2(eb−ea)的大小,亦即比较(b−a)(ea+eb)−2(eb−ea)与0的大小.

以b为主元,视a为参数,记函数

求导得

得F′(x)在(a,+∞)上单调递增,则F(x)＞F(a)=0,即F(b)＞0,则若f(x)min＜g(x)max,则

点评可见利用主元法可轻松破解该类高考压轴题!主元法可操作性强,按部就班,考生容易掌握!主元法中的两“元”必须相互独立,否则不可以用主元法证明!

强化训练题

1.已知函数f(x)=ln(1+x)−x,g(x)=xlnx.

(1)求函数f(x)的最大值;

(2)设0＜a＜b,求证:

2.2010年陕西理21题.

突破策略六利用“公切线”法证明不等式

题目同例1.

解析设φ(x)=ex,h(x)=ln(x+2)的公切线为y=kx+b设两切点分别为:M(m,em),N(n,ln(n+2)).

利用切线的斜率得:

当n=−1时,M(0,1),N(−1,0),对应公切线为y=x+1.(当n=e−2时,,对应公切线为)我们不妨取公切线为y=x+1.利用构造函数法易证:

但两不等式不同时取等号,所以ex＞ln(x+2).所以,当m≤2,

所以f(x)＞0.

点评利用”公切线”法证明函数型不等式,方法相当精妙!可实现精准放缩,证明方向也相当明确.但此方法只适用于一凸、一凹函数类型,若两函数同为凸函数或凹函数,可对不等式作适当变形,转化为一凸、一凹函数类型,再用”公切线”法证明.

突破策略七

含有ex,lnx,xlnx的函数型不等式可放缩为如下一次函数形式,我们可称之为函数放缩的“一般式”.

下面详细举例说明这几个放缩式的应用,可以说该放缩法是快速解决函数不等式压轴题的通性通法之一.

(i)的证法一设f(x)=ex−kx,(k＞0)所以f′(x)=ex−k.

当x＞lnk时,f′(x)＞0;当0＜x＜lnk时,f′(x)＜0.所以f(x)min=f(lnk)=k−klnk,所以f(x)≥f(x)min=k−klnk.所以ex≥kx+k−klnk,(k＞0).

(i)的证法二(利用切线系方程证明)设函数y=ex在点处的切线斜率为k(k＞0),因为y′=ex,则.故函数y=ex在点处的切线为y=kx+k−klnk,(k＞0),所以ex≥kx+k−klnk,(k＞0).

(ii)的证明设f(x)=lnx−kx,(k＞0).则有

(iii)的证明设f(x)=xlnx−kx,(x＞0,k∈R).所以f′(x)=lnx+1−k.当 0＜x＜ek−1时,f′(x)＜0,f(x)递减;当x＞ek−1时,f′(x)＞0,f(x)递增.所以f(x)min=f(ek−1)=−ek−1,故f(x)≥f(x)min=−ek−1.因此xlnx≥kx−ek−1,(x＞0,k∈R).

1.函数型不等式(i)应用举例

题目同例1.

解析(1)略.

(2)证明:当m≤2时,

即证ex＞ln(x+2).

由函数型不等式(i)得:ex≥kx+k−klnk,(k＞0).即只需证:

设φ(x)=ln(x+2)−[kx+k−klnk],所以

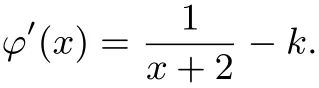
不妨取k=1或,利用ex≥x+1或均可证得原不等式!

点评本放缩的方法按部就班,操作性强,可实现精准放缩.在实际解题中,我们只要通过观察得到k,使即可,可以说该解法是快速解决这类函数型不等式压轴题的通性通法.

2.函数型不等式(ii)的运用举例

例7求证:ex＞2x+lnx,(x＞0).

解析由函数数型不等式(ii)得:lnx≤kx−lnk−1,(k＞0),所以lnx+2x≤(k+2)x−lnk−1,即证:ex≥(k+2)x−lnk−1.设h(x)=ex−[(k+2)x−lnk−1],(x＞0,k＞0).h′(x)=ex−(k+2).当x＞ln(k+2)时,h′(x)＞0,h(x)递增;当0＜x＜ln(k+2)时,h′(x)＜0,h(x)递减.所以

原不等式得证!

整理该证明过程如下:

点评该解法是解决这类函数型不等式压轴题的通性通法!此题其实可利用常见函数型不等式或进行放缩即可得证,但对于本题lnx≤x−1,(x＞0)实效.另该题也可采用策略二证明,转化证明:0),设.所以f(x)min＞g(x)max,所以ex＞2x+lnx,(x＞0).即转化为两个函数的最大、最小值的比较问题,证明过程相对较简便,但此类尝试要对含ex,lnx(x＞0)的组合函数图像和性质非常熟悉,否则不易变形转化证明.故要注意题型、方法的总结感悟,提升解决此类函数导数压轴题的能力.

3.函数型不等式(iii)的应用举例

例8求证:ex+ex−3＞1−x(1+lnx)(x＞0).

解析原不等式即证:

由函数型不等式(i)得:

由函数型不等式(iii)得:

点评当证明思路不明确时,可采用该一般性的证明方法寻找解题思路,但证明过程采用综合法书写会较简便.另该题也可设f(x)=ex+ex−3,(x＞0).g(x)=1−x(1+lnx),(x＞0)转化为两个函数的最大、最小值的比较大小问题,易证,所以f(x)＞g(x)原不等式得证.解题时要不断总结感悟、解题思路和方法,提升解决此类导数不等式压轴题的解题能力.

策略八含参数问题,可优先考虑消去参数、换元,再构造函数证明,有时还需构造局部函数再次求导,也可考虑分离参数,再构造函数,常需分类讨论.

例9 已知x1,x2是函数f(x)=ex−ax的两个零点,且x1＜x2,求证:x1x2＞1;x1+x2＞2.

解析因为x1,x2是函数f(x)=ex−ax的两个零点,

设m(t)=t−1−tlnt(t＞1),则m′(t)=−lnt＜0,所以m(t)在(1,+∞)上递减.所以m(t)＜m(1)=0,所以φ′(t)＜0,所以φ(t)在 (1,+∞)上递减.因此φ(t)＜φ(1)=0,所以g′(t)＜0,g(t)在 (1,+∞)上递减,但g(1)没有意义.由高等数学中的洛必达法则,

点评本题考查了导数在研究函数中的综合运用,解答的关键在于利用消元思想,先消去参数,转化为含双变量x1,x2的不等式,再利用“二元化一元”的思想,通过等价换元构造函数法得证,但有时需用到高等数学中的洛必达法则.

例10 已知函数f(x)=ln(x+1)+ae−x−a.

(1)当a=1时,证明:f(x)在(0,+∞)上是增函数;

(2)若对任何x∈[0,+∞),不等式f(x)≥0恒成立,求实数a的取值范围.

解析(1)略.

(2)因为∀x∈[0,+∞),不等式f(x)≥0恒成立,所以成立.设,

不好作进一步处理判断求最小值,但利用洛必达法则,问题便可迎刃而解!其解答过程如下:

因为

所以a≤1,所以实数a的取值范围是(−∞,1].

点评本题主要考查利用导数研究函数性质、不等式恒成立问题以及参数取值范围问题,考查分类讨论、转化与化归解题思想及其相应的运算能力.本题采用分离参数思想,转化为求函数的最小值,但φ(0)没有意义,利用高等数学中的洛必达法则,可以使得问题难点得到轻松解决!含参数型函数导数压轴题的解题策略限于篇幅,笔者此处不详细举例说明,笔者将另文讨论.

总之,证明或解复杂的函数型不等式(包括不等式恒成立或存在性问题),最终还是化归为构造函数,再利用导数研究相应的性质,充分发挥导数的工具性和应用性的作用,往往可以获得问题的解决!教学中要引导学生熟练掌握此类函数型不等式压轴题的解题突破策略,做好题型的归类和方法的总结,掌握好通性通法,如构造函数法、常见函数型不等式放缩法、主元法、分离变量法等,加强对转化与化归、数形结合、函数方程、分类讨论等数学思想方法的渗透,辅之以一定量的强化训练,尖子生利用函数导数压轴题得高分也是可能的,更会是必然的!

二.教学和选题的建议

1.“倡导积极主动、勇于探索的学习方式”是高中数学新课程的基本理念之一.章建跃博士认为:“从数学知识发生发展过程的合理性,学生思维过程的合理性上加强思考,这是落实数学学科核心素养(数学抽象、逻辑推理、数学运算、直观想象、数学建模、数据分析等)的关键点.”在实践新课程的过程中,教师要积极主动地贯彻落实这一基本理念.数学学习的核心是思考,离开思考就没有真正的数学.教学设计应该遵循如何促进学生主动建构,如何引导学生深度学习,如何培养学生数学思维能力,发展核心素养.教师要重视问题情境的创设,在此基础上向学生提出恰当的问题,努力推进学生的数学活动:动手操作、分组学习、自主探究、合作交流!教育的根本目标是育人,数学教育理应把育人放在首位.“从数学学科教学的角度,作为人的发展,就体现在发展人的认知力.”认知力的重要含义就是研究新情况、解决新问题的能力,其中蕴含着创新、创造的能力.数学课要把发展学生的认知力作为教学的最大目标,着眼于学生的长远发展利益,实现其终身可持续发展.

2.从国际视野的角度看,当今的数学教育趋势就是以理解为价值取向!以问题解决为价值取向!以数学探究为价值取向!因此,科学、合理、现代的数学高考就是要考数学理解!考数学问题解决!考数学探究!教师要抓好课堂教学,在重视基础知识和基本技能教学的同时,注重提升学生对数学思想方法和数学本质的理解水平.教师要精选习题,多设计能考查数学主体内容、体现数学素质的题目,反映数、形运动变化的题目,研究型、探索型或开放型的题目,让考生独立思考,自主探索,发挥主观能动性,研究问题的本质,寻求合适的解题工具,梳理解题程序,为考生展现创新意识、发挥创造能力创设广阔的空间!选题要注重基础性、典型性、综合性、启发性、开放性和探究性,且要注重一般性的解题规律和方法(即通性通法);要精选一些一题多变、一题多解、多题归一、有层次、有拓展的题目开阔学生思路,使学生能有新的体会和收获;要重视课本中的典型例题、习题和最近几年的高考题、高考模拟题,多些对课本例题、习题和高考题的进行改编与拓展.课堂教学中教师要引导学生重视对函数与方程、转化与化归、数形结合、分类讨论等数学思想方法的感悟及解题规律的总结与提升,提高学生的数学解题能力与数学素养!

强化训练题

1.(2016年全国卷I第21题)已知函数f(x)=(x−2)ex+a(x−1)2有两个零点.

(1)求a的取值范围;

(2)设x1,x2是f(x)的两个零点,证明:x1+x2＜2.

y=e(x−1)+2.

(1)求a,b;

(2)证明:f(x)＞1.

(1)求k的值;

(2)求f(x)的单调区间;

(3)设g(x)=(x2+x)f′(x),其中f′(x)是f(x)的导函数.证明:对任意x＞0,g(x)＜1+e−2.

4.已知函数f(x)=xe−x(x∈R).

(1)求函数f(x)的单调区间和极值;