基于PSO-SVR航站楼CO2浓度时间序列预测

陈静杰，陈 晨，顾泽龙

（中国民航大学 电子信息与自动化学院，天津 300300）

随着我国国民经济的发展和人们生活水平的日益提高，越来越多的旅客选择乘坐飞机出行。航站楼作为旅客空陆交通的集散中心，人流密度大。《室内空气质量标准（GB/T18883-2002）》[1]中规定室内CO2浓度的限制是1000 ppm，因此，建立合理精确的CO2预测模型有助于监控航站楼里的CO2浓度，保证旅客的舒适度。

国内外对于气体浓度的预测研究，早期应用比较多的是神经网络方法[2-3]、多元回归方法[4]等。然而，这些传统的预测方法只有在样本数量非常大的情况下才能达到理想的预测效果。本文研究内容是基于小样本的预测，而且航站楼里CO2浓度的变化是高度非线性，这使得很多传统的预测方法难以建模预测。

SVR是由Vapnik[5]提出的函数拟合工具，对解决小样本、非线性、高维数等问题具有很强的泛化能力。SVR方法在非线性时间序列预测中已经得到广泛使用[6-10]。本文拟采用SVR方法来预测航站楼CO2浓度，并使用粒子群优化算法对SVR参数优化，进一步提高预测模型精度。

1 SVR原理

支持向量回归（SVR）处理非线性回归预测问题时的基本思想[5，11]是通过使用非线性映射φ（·）将输入的样本数据映射到高维特征空间H中，进而将非线性问题转化为线性问题。建立线性回归方程为

式中：w为高维特征空间H的权值向量；φ（·）为将输入向量xi从输入空间映射到高维特征空间H中的映射；b为线性回归方程的偏置项。根据结构风险最小化原理，f（x）函数应该使如下风险函数最小：

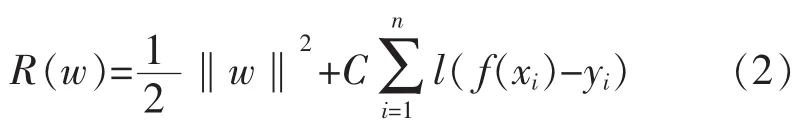
式中：C为惩罚系数，控制对超过不敏感值误差的样本数据的惩罚程度；l（ f（xi）-yi）为损失函数。根据航站楼CO2浓度回归预测的特点，本文的损失函数选取线性不灵敏损失函数，其表达式为

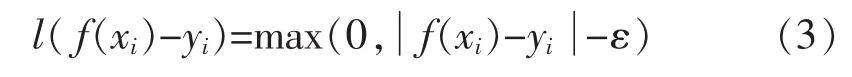
式中：ε为不敏感系数，控制着预测模型精度。

由于需要处理函数f（x）在ε精度下不能回归的数据，引入松弛因子ξ和ξ*，于是航站楼CO2浓度回归预测问题就转化为求解如下约束条件下最小化问题：

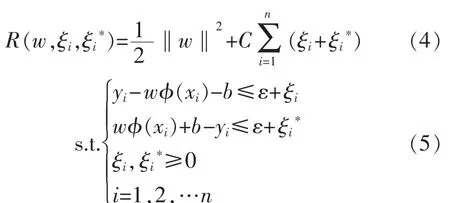
对式（4）采用拉格朗日乘子法和对偶原理处理，并引入满足 Mercer条件核函数 K（xi，xj）＝φ（xi）φ（xj）加以变换，得到式（4）的对偶问题：

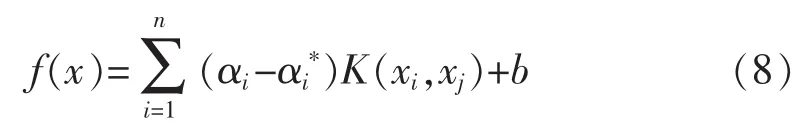
由于高斯核函数在预测时间序列数据时具有明显的优势，它具有良好处理样本输入与输出之间复杂非线性关系的能力，而且具有计算效率高、参数少、参数选取计算量较小等优点[12]。因此本文选取高斯核函数 K（xi，x）=e-γ‖xi-x‖2作为SVR的输入的核函数。最终得到的决策函数为

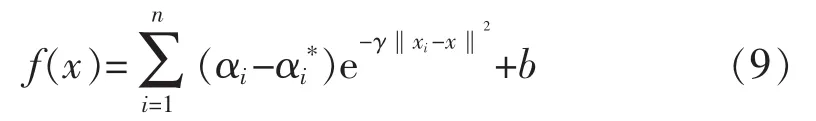
2 基于SVR的时间序列预测模型

2.1 模型构建

对于时间序列｛x1，x2，…，xn｝，｛xn｝是预测的目标值，建立自相关输入 xn=（xn-1，xn-2，…，xn-m）与输出 yn=f（xn）之间的映射关系 f：Rm→R，其中 m 为嵌入维数。经过变换之后，得到用于支持向量机学习的样本为

对SVR进行训练的回归函数为

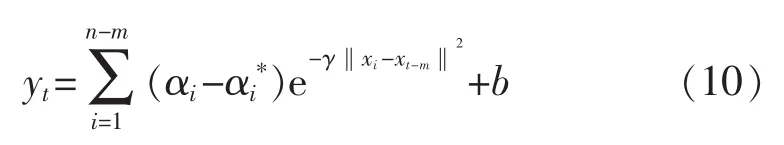
由此得到第一步预测为

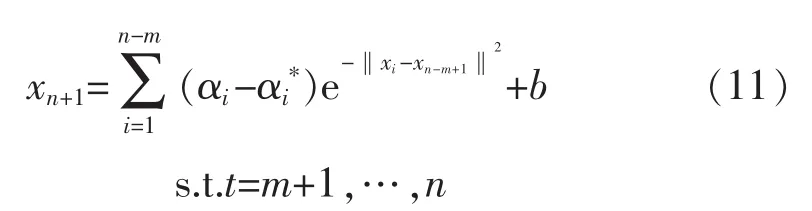
式中，xn-m+1=｛xn-m+1，xn-m+2，…，xn｝，得到一个样本xn-m+2＝｛xn-m+2，xn-m+3，…，xn+1｝，则第二步预测为

以此类推可以得到第l步预测：

式中：xn-m+l＝｛xn-m+l，…xn+1，…，xn+l-1｝。

2.2 模型阶数确定

在时间序列预测中，对于嵌入维数的选取还没有严格的理论依据。本文根据最终预报误差FPE准则评价模型的预测误差，其公式为

式中：ntr为训练数据的个数；k为需要确定的嵌入维数；xt，分别为实际值和预测值。当 k变化时，FPE（k）也相应发生变化，因此可以寻找到一个最优值kbest使得FPE最小。此时的嵌入维数m=kbest。

2.3 模型评价标准

本文利用均方误差MSE、平方相关系数r2来评判SVR回归模型性能的优劣，相关表达式如式（15）、（16）所示。MSE 的值越小，说明模型的预测精度越高；r2越接近于1，表明模型回归拟合效果越佳。

式中：xi、分别为实测值和预测值；n 为样本数。

3 基于PSO算法的SVR时间序列模型参数寻优

3.1 PSO原理

PSO是由J.Kenney和R.Eberhart[13]提出的一种高效多维并行的全局寻优算法，该算法是一种采用速度-位置搜索模型、通过个体间的协作与竞争实现多维空间中最优解搜索的智能优化算法。其数学表示为设在D维搜索空间中，由n个粒子组成一个种群。该种群中第i个粒子于t时刻在D维搜索空间的位置为，速度为，当前时刻的个体极值为pbest，全局极值为gbest。该粒子于t+1时刻在D维搜索空间的位置为，速度为在每次迭代过程中，粒子跟踪个体极值、全局极值以及自己上一次迭代状态来更新当前迭代的速度和位置，其迭代公式为

式中：Vt、Vt+1、Xt、Xt+1表示粒子当前的时刻以及下一时刻的速度和位置；i=1，2，…，n；ω 为权重因子；c1和 c2表示学习因子，均为非负常数；r1和 r2为［0，1］之间的随机数。

3.2 PSO-SVR算法模型参数寻优

SVR模型参数寻优主要寻优惩罚参数C、核函数参数γ。参数C是经验风险和置信范围的裁决，参数γ影响数据在高维空间中分布的复杂度[14]。目前常用的支持向量回归机模型参数寻优方法是GS-SVR、GA-SVR、PSO-SVR等。GS-SVR寻优参数过程中，计算量大且搜索参数的范围容易受到局限；GA-SVR寻优参数时运算耗时长，参数设置复杂，并具有不稳定性；PSO-SVR算法则极大地提高了预测精度和收敛速度，且调节参数少，简单易行，非常适合SVR函数的参数寻优。PSO-SVR寻优参数的算法流程如图1所示。些取出数据构成试验数据。试验数据序列如图4所示。

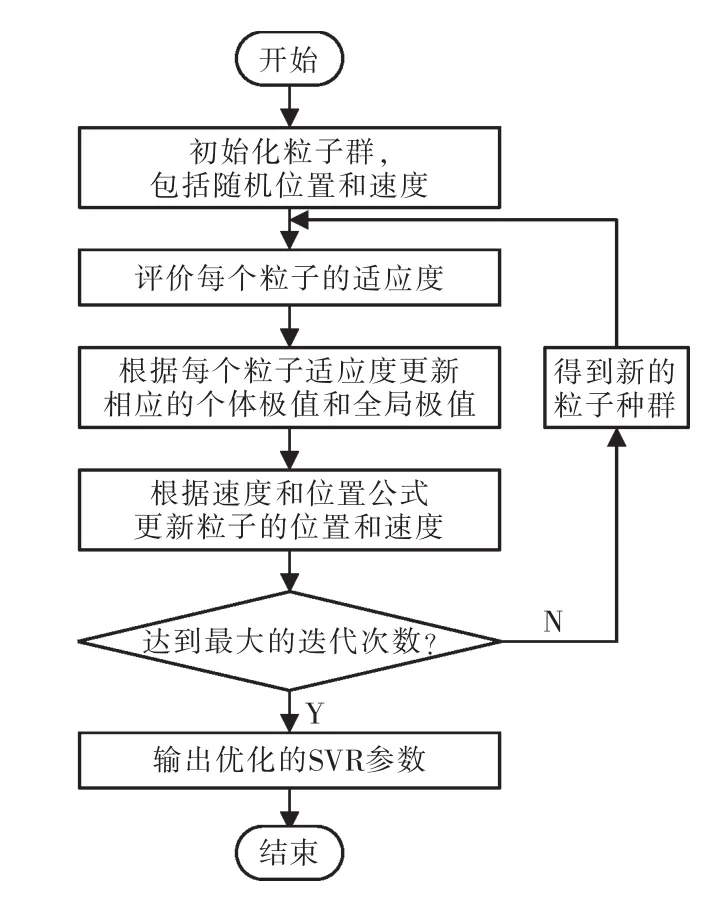
图1 PSO-SVR寻优参数流程Fig.1 PSO-SVR optimization parameters flow chart

4 基于PSO-SVR算法航站楼CO2浓度模型建立

4.1 数据采集

本文利用自行设计的机场大气环境数据采集系统来采集航站楼的CO2浓度数据。该系统利用CO2传感器采集CO2浓度，利用STM32F103ZET6作为主控芯片去控制采集过程。使用无线模块WLK01L39与上位机通信，并在上位机中读取并显示CO2浓度数据。机场大气环境数据采集系统原理如图2所示，机场大气环境数据采集系统实物图如图3所示。

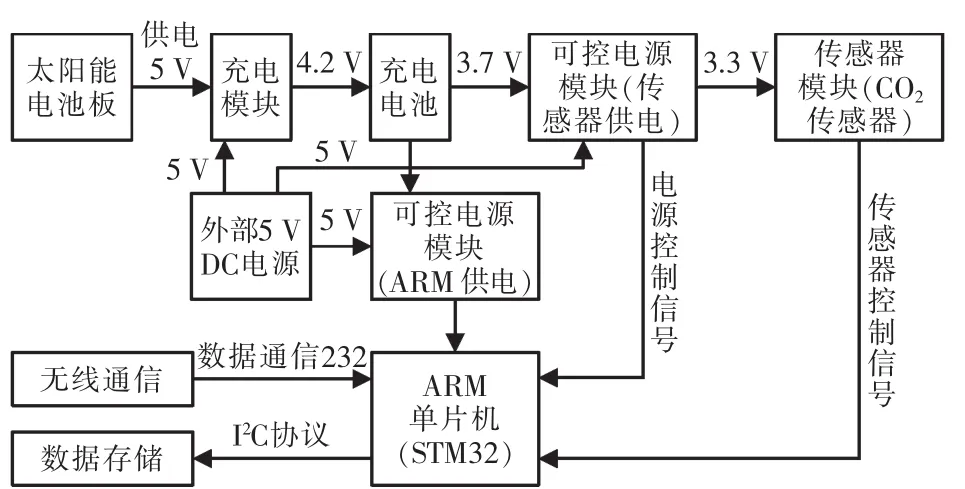
图2 机场大气环境数据采集系统原理Fig.2 Principle diagram of airport atmospheric environment data acquisition system

图3 机场大气环境数据采集系统实物Fig.3 Physical map of airport atmospheric environment data acquisition system

4.2 数据处理

为了降低建模误差以及提高计算效率，需将数据进行归一化处理。本文采用最小-最大归一化法将数据归一化到［0，1］之间。表达式为

4.3 模型建立

本文以2016-08-28于天津滨海国际机场T2航站楼采集的CO2浓度数据为研究对象，将采集的CO2浓度数据从7：00～19：00每隔5 min取1个数据，将这

图4 试验数据序列Fig.4 Experimental data series

将试验数据归一化处理，然后把试验数据的前132组数据作为训练数据，后12组数据作为测试数据。采用最小信息预报准则评价模型的预测误差，以误差最小来确定模型阶数m。经过计算确定m=6时，FPE最小，其值为0.0033。

现在利用PSO-SVR方法来建模。初始化粒子群算法各个参数：c1=1.5，c2=1.7，种群数量为 20，终止代数为200。利用PSO算法对试验数据的训练集数据进行参数寻优，得到样本的适应度曲线，如图5所示。寻优得到SVR模型中最佳惩罚因子C=20.7388，核函数参数γ=0.01。

图5 PSO算法优化SVR的适应度曲线Fig.5 PSO algorithm to optimize the SVR fitness curve

4.4 模型验证

为验证建立的航站楼CO2浓度模型的有效性，用测试集数据对该模型进行测试。利用Matlab软件并结合Libsvm支持向量机工具箱对航站楼CO2浓度进行预测仿真。经过12步预测，得到测试集的均方误差MSE=0.0063，平方相关系数r2=97.4608%。

4.5 模型对比

4.5.1 SVR参数寻优方法对比

分别用网格搜索法和遗传算法对SVR模型参数寻优，建立GS-SVR模型以及GA-SVR模型。训练集和测试集与PSO-SVR方法选取相同，参数寻优结果如表1所示。

表1 3种不同方法对SVR参数寻优结果对比Tab.1 Comparison of three different methods for SVR parameter optimization

由表1对比可知本文用的PSO算法优化SVR测试集的均方差最小，相关系数最大，说明本文建立的PSO-SVR模型比GS-SVR模型和GA-SVR模型参数优化法预测精度更高，模型泛化能力更佳。

4.5.2 PSO-SVR模型与BP神经网络模型对比

选用三层拓扑结构的BP神经网络来建立航站楼CO2浓度的预测模型。其中输入层有5个节点，隐含层有6个节点，隐含层的激活函数为tansig，输出层有1个节点，输出层的激活函数为logsig。学习速率为0.01，最大训练次数为1000，目标误差为0.0001。训练集和测试集数据与PSO-SVR方法选取相同。BP神经网络建立的预测模型经过351步，耗时2 min 3 s（电脑配置：Intel Core i7、8 G 内存、Win7 32位），模型测试集的均方误差为0.0188，平方相关系数为94.0521%。由此可见SVR模型预测精度明显高于BP神经网络，而且BP神经网络训练耗时长且易出现“过学习”现象，泛化能力不强，因此SVR方法更加适用于航站楼CO2浓度的预测模型的建立。

把以上4种方法测试集建模输出的12步预测结果进行反归一化，其预测结果如图6所示。从预测结果图可以直观地看出，PSO-SVR方法预测集输出拟合效果最好，建立的PSO-SVR预测模型是合理、可靠的。

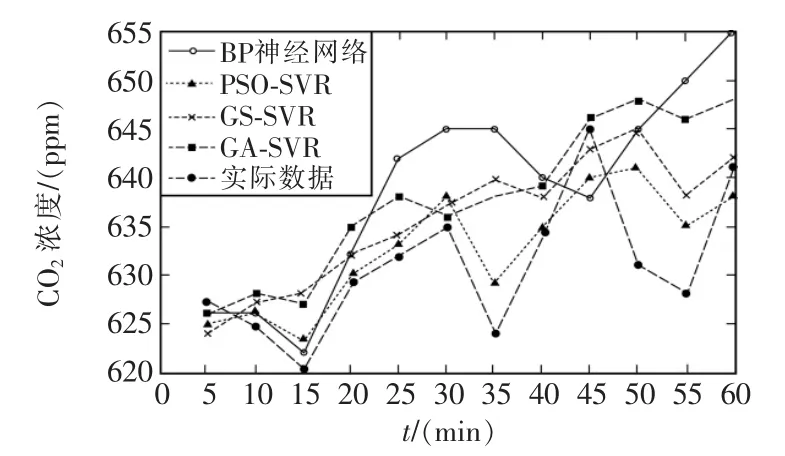
图6 测试集的预测结果Fig.6 Prediction results of test set

5 结语

航站楼CO2浓度时间序列预测是一个非常复杂的过程，由于影响CO2浓度因素很多，所以会使得预测过程具有高度的复杂性。SVR具有非常优良的学习能力、泛化性以及非线性，结合PSO算法的全局寻优能力，建立PSO-SVR模型对航站楼CO2浓度进行预测。为了与本文所提出的PSO-SVR模型作对比，分别利用网格搜索法、遗传算法对SVR模型参数进行寻优，并与传统的BP神经网络模型作对比，试验结果表明SVR模型性能明显优于BP神经网络，而且PSO-SVR模型的参数优化性能更佳。研究成果在一定程度上可为航站楼监控CO2浓度含量提供参考。

[1]中华人民共和国卫生部.室内空气质量标准（GBT18883-2002）[S].北京：中国标准出版社，2002.

[2]ZHAO Jin-xiao，JIN Hong-zhang，YU Guang-hua.Coalmine gas concentration forecasting based on chaot-ic theory and neural network model[C]//2010 Third International Conference on Information and Computing（ICIC 2010），Wuxi，IEEE Computer Society，2010：35-38.

[3]HOU Yu-hua，CHENG Jian，LI Shi-yin.Forecasting coalmine gas concentration based on RBF neural network[C]//International Conference on Information Acquisition（ICI-A2007），Seogwipo-si：IEEE Computer Society，2007：192-194.

[4]陈丽琼，虞才珠.基于多元回归法的气体浓度预测方法[J].上海应用技术学院学报：自然科学版，2013，13（1）：75-79.

[5]Vapnik V N.The nature of statistical learning theory[M].New York：Springer-Verlag，1995.

[6]CHEN Kuan-yu.Evolutionary support vector regression modeling for Taiwan stock exchange market weighted index forecasting[J].Journal of American Academy of Business，2006，8（1）：241-247.

[7]Kim K J.Financial time series forecasting using support vector machines[J].Neural Computing，2003，31（14）：307-319．

[8]王炜，刘悦，李国正，等.中国大陆强震时间序列预测的支持向量机方法[J].地震，2005，25（4）：28-34.

[9]李立辉，田翔，杨海东，等.基于SVR的金融时间序列预测[J].计算机工程与应用，2005，41（30）：221-224.

[10]李万庆，李海涛，孟文清.基于支持向量机的降水量混沌时间序列预测[J].统计与决策，2007（19）：9-11.

[11]Vapnik V N，Golowich S E，Smola A.Support Vector Method for Function Approximation，Regression Estimati on，and Signal Processing[M].San Mateo，CA：NIPS’8，1996.

[12]Nanye L，Daniel G，Guilherme J，et al.Application of support vector regression to genome-assisted prediction of quantitative traits[J].Theoretical and Applied Genetics November，2011，123（7）：1065-1074.

[13]EBERHART R，KENNEDY J.A new optimizer using particle swarm theory[C]//Proceedings of the Sixth International Symposium on Micro Ma chine and Human Science，Nagoya，Japan：IEEE，1995：39-43.

[14]郭美丽，覃锡忠，贾振红，等.基于改进的网格搜索SVR的话务预测模型[J].计算机工程与科学，2014，36（4）：707-712.