高速公路交通量时空特性分析

娄岩，弓晋霞，王俊辉，李松江，田迎华，王鹏

（1.长春理工大学 计算机科学技术学院，长春 130022；2.吉林省高速公路管理局，长春 130028）

高速公路交通量，指单位时间内通过道路某断面的交通流量。交通量特性的分析，是智能交通［1］管理系统重要的研究基础，有助于交通量预测、行程时间预测以及收费预测等［2-6］研究。国内外研究者在高速公路交通量特性分析方面进行了大量的研究，将其应用于实践中，并取得了一定的成果。罗京等人研究了降雨对高速公路交通流特征的影响［7］；沈强儒对高速公路菱形立交关键部位交通量的适应性与技术指标进行研究［8］；杨鹏等人基于综合调查方法下对高速公路交通量进行分析研究［9］；李宏德基于运动学的高速公路汽车慢行对交通量的影响进行分析［10］。由于高速公路交通量会随着时间和空间的变化而随机变化，本文选用东北某省高速公路交通量数据，从时间和空间的两个角度对交通量特性进行定性和定量的分析，得出交通量具有时间序列性、周期相似性和空间序列性，并利用相关性计算方法对交通量时空特性分布规律进行深入的分析。

1 数据来源

本文实验数据选取东北某省2015年7月13日到8月9日高速公路收费系统部分路网的收费数据。通过统计各个收费站出入口交通量数据、收费站之间点到点的OD交通量数据，以及对高速公路路网的分析研究，以15min为时间间隔计算出各个路段的交通量数据。如图1所示，本文选取距离为34.11km的路段作为研究路段，记为“0”路段。“1、2、3”为下游路段，“4、5、6”为上游路段。

图1 路段示意图

2 高速公路交通量时空特性分析

2.1 交通量时间序列性

时间序列性，指在同一统计指标下研究对象的数据随着时间先后顺序排列起来的一组数据。如图2所示，为2015年7月13日到8月9日高速公路路段“0”星期一到星期日的交通量数据分布趋势图。从图中可以看出，随着时间的推移，交通量分布也在不断发生变化，以天为单位排列成一组一组有规律的交通量数据序列，即高速公路交通量时间序列性。同时，交通量分布曲线存在两个明显的高峰时段，这是由于人们上班作息规律性所形成的。休息日期间，由于人们远途旅行的增加导致高速公路交通量高于工作日。

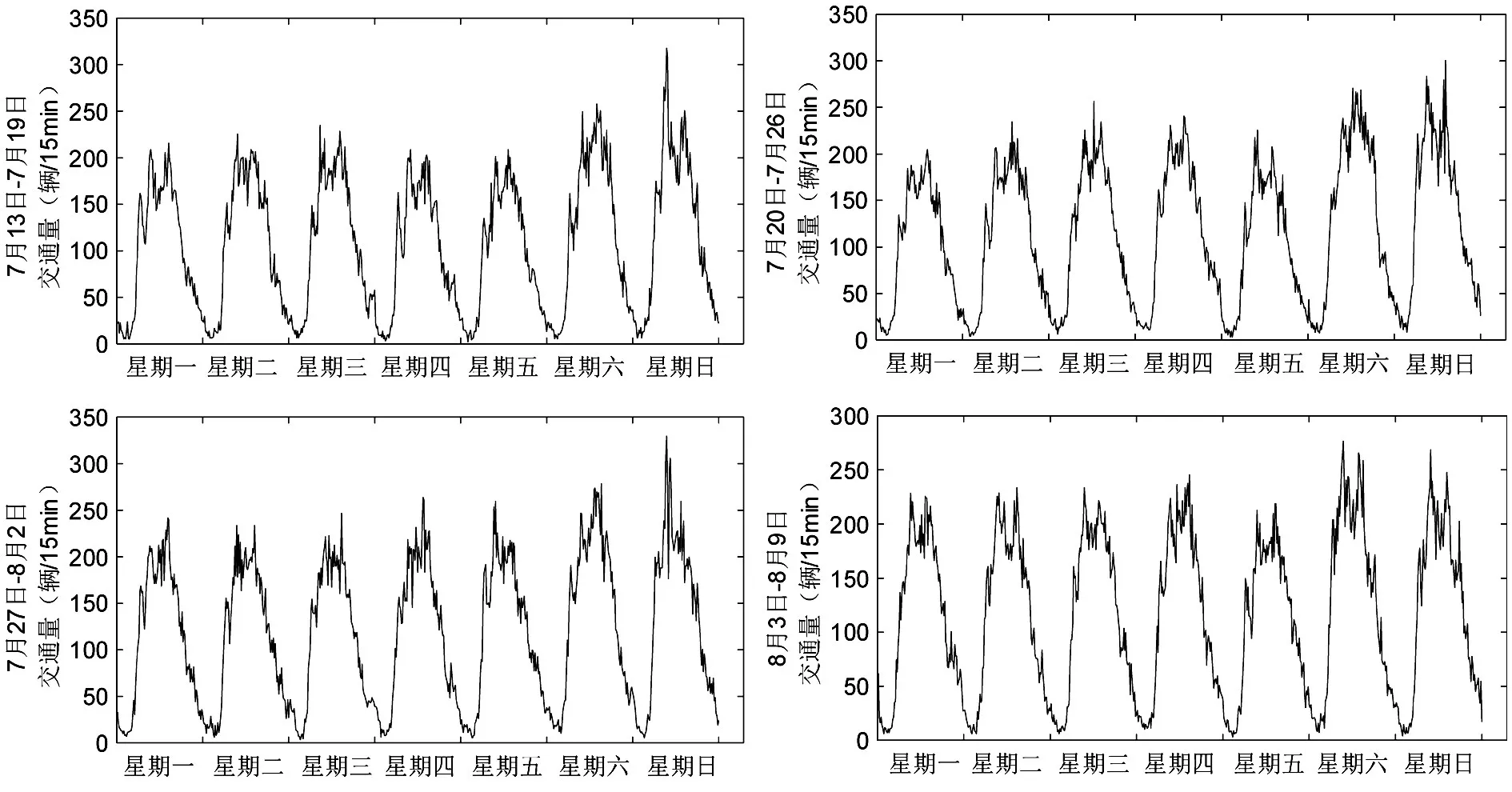
图2 交通量时间序列性分布图

高速公路当前时段交通量与前几个时段的交通量之间存在着一定的联系，因此本文利用相关性计算方法对时间序列特性进行进一步的定量分析。假设目标时段交通量时间序列列向量为前n个时间段的交通量时间序列列向量构成时间序列矩阵代表前1个时间段的交通量时间序列列向量，以此类推即代表前n个时间段的交通量时间序列列向量。利用公式（1）分别对前10个时段交通量数据与目标时段交通量时间序列列向量进行相关性计算，结果如表1所示。

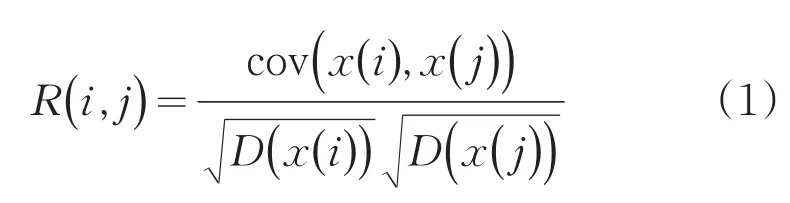
表1 时间序列相关性

表1为7月13日到7月19日以15min为时间间隔，目标时段交通量数据列向量与前8个时段的交通量数据列向量的相关性。以工作日星期一为例讨论，目标时段交通量与前1个时间段内的交通量之间的相关性为0.975，前8个时间段的交通量相关性为0.780。从表中可知，随着时间间隔与目标时段距离的增加，相关性逐渐下降。

2.2 交通量周期相似性

高速公路交通量数据产生于人们的出行，人们生活作息出行周期规律性直接影响着交通量数据的特征。结合图2，分别以“星期”、“天”为单位进行比较分析，可知交通量呈现出不同程度的相似性变化规律，即高速公路交通量的周期相似性。由于休息日与工作日分析方法相同，本文以工作日为例进行讨论。对每个星期三的交通量数据分布趋势进行统计，如图3（a）所示。将第四个星期的前四天交通量数据分布趋势进行统计，如图3（b）所示。比较图3（a）和3（b）可以看出，随着时间的推移，两组交通量数据曲线都呈现出很明显的周期相似特性。图3（a）交通量数据基本拟合成一条“M”曲线，图3（b）相对而言较为离散，其拟合性与图3（a）相比较差，故推测高速公路交通量周期性的时间尺度不同，会导致周期相似程度不同。

为了对不同时间尺度的周期相似程度进行进一步的分析，假设p个周期的交通量数据列向量构成周期相似性矩阵分别对图3所示两组交通量周期相似系数进行计算，即p个周期的交通量数据向量两两间相关系数的平均数，其表达式为：

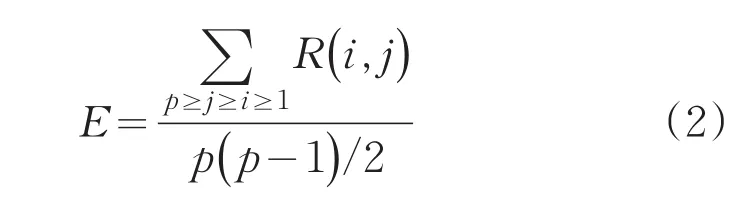
图3 周期相似性交通量分布图

表2 周期相似系数

表2为图3两组交通量的相关性系数与相似系数。R1（15，22）代表第一组以星期为单位进行讨论的7月15日和7月22日的相关系数，E1为第一组的周期相似性系数；R2（3，4）为第二组8月3日和8月4日的相关系数，E2为第二组的周期相似性系数，以此类推。第一组的相似系数为0.9671，第二组的周期相似系数为0.9098。分别对两组的相似系数以及两个周期之间的相关系数进行对比可知，每周星期三的交通量周期相似性高于第五周连续工作日的交通量周期相似性。综上得出，以星期为时间尺度的同“星期几”的交通量周期相似性高于以“天”为时间尺度的交通量周期相似性。

2.3 交通量空间序列性

高速公路路网系统由各个路段连接组成，路网内某一路段交通量与其上下游路段交通量分布具有一定的关联性。如图4中（a）、（b）、（c）、（d）、（e）、（f）分别为路段“1、2、3、4、5、6”与目标路段“0”之间2015年8月3日到7日连续一周工作日480个时间段的交通量拟合图，可以发现各个路段交通量基本上都分别拟合于一条不同的直线，但拟合程度呈现不同的状态，其拟合程度呈现于表3中。表3显示路段“1”与研究路段“0”之间的决定系数高于其它下游路段，EMSE低于其它下游路段；路段“4”与研究路段“0”之间的决定系数高于其它上游路段，EMSE低于其它上游路段，即高速公路交通量存在空间序列性。

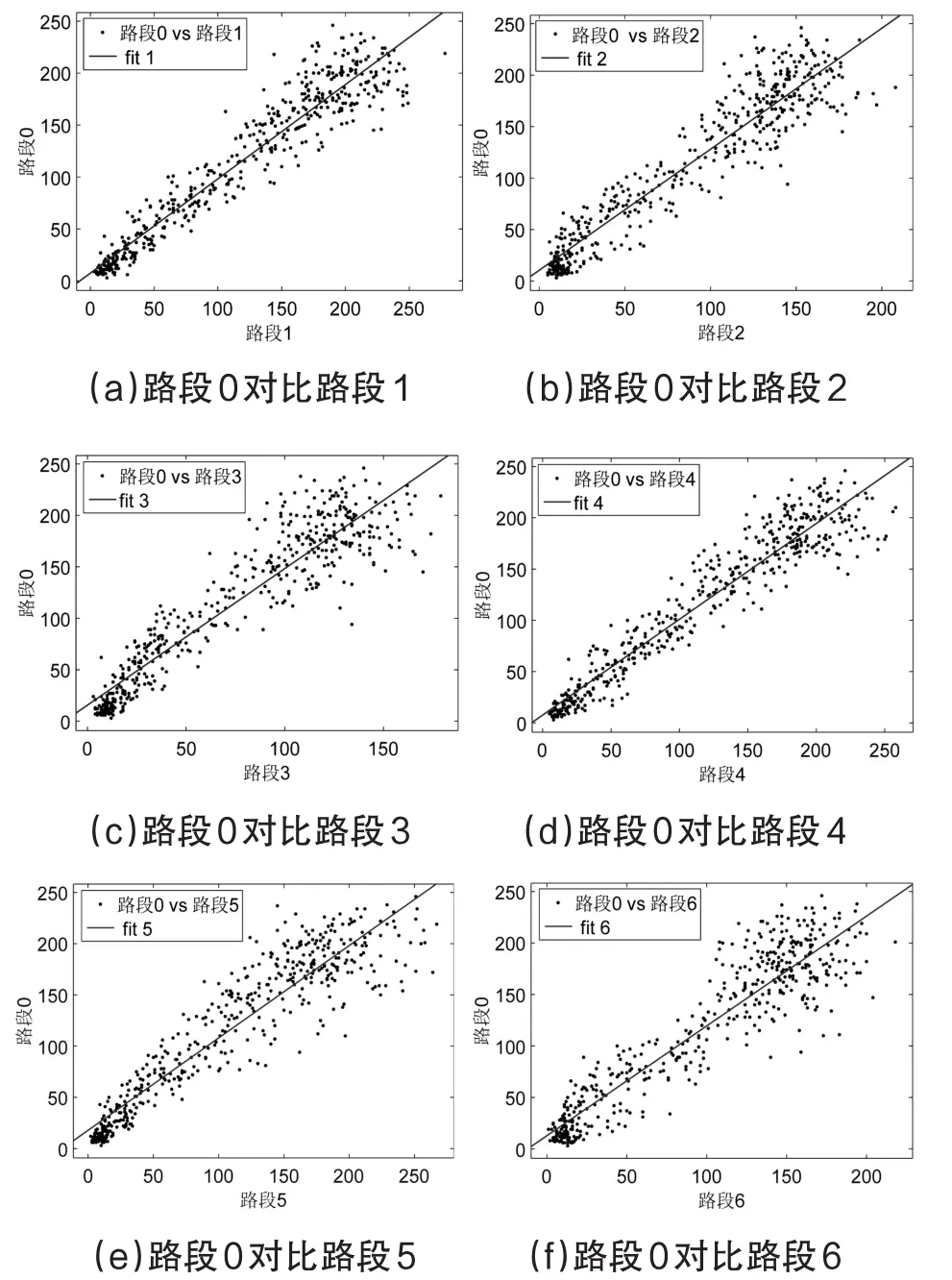
图4 研究路段“0”与各个路段交通量拟合图

由于高速公路不同路段的交通量会受到人文地域、自然环境、天气条件等多种因素的影响，考虑路段之间的空间相关性时不能一概而论，需要对目标路段与其相邻路段之间的交通量相关性进行计算，从而确定上下游路段之间的相互依赖性，进而对交通量的空间序列特性进行分析与讨论。假设l个相邻路段的交通量数据组成空间序列矩阵利用公式（1）分别对6个相邻路段数据与目标路段的交通量数据之间的相关性进行计算，计算结果如表4所示。

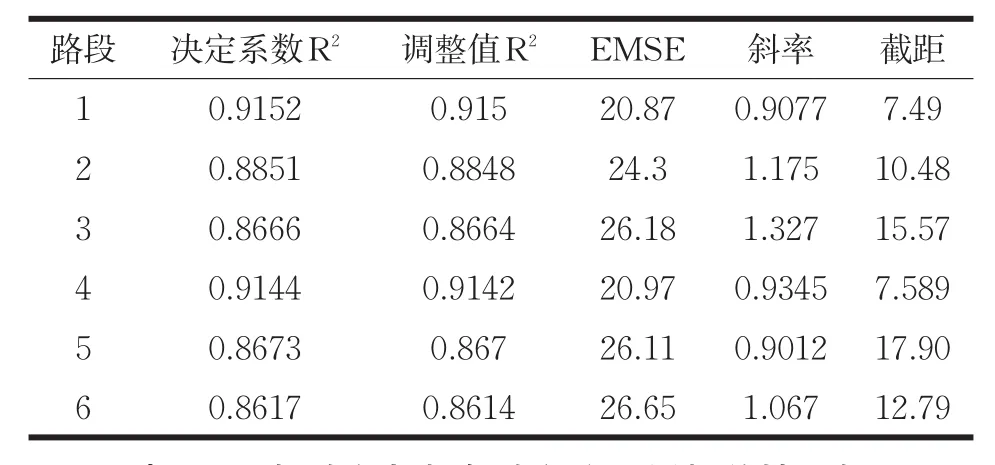
表3 研究路段与相邻路段交通量拟合程度系数

表4 目标路段与相邻路段交通量相关性系数

从表4可知，各个路段交通量数据与目标路段的相关性都大于0.9，其中相邻下游路段的相关性为0.961，相邻上游路段的相关性为0.956。结合图1和表4可知，随着与目标路段间隔距离的增加，相关性逐渐下降。

3 结束语

（1）通过对高速公路交通量数据分布趋势进行分析，得出交通量具有时间序列性、周期相似性和空间序列性。

（2）利用相关性计算方法对交通量时空特性进行研究，发现历史时段交通量与目标时段交通量之间的相关性，随着与目标时段时间距离的增加逐渐下降。

（3）随着时间尺度不同，交通量周期相似性程度呈现不同。

（4）上下游路段交通量与目标路段交通量之间的相关性，随着与目标路段距离的增加不断下降。

（5）高速公路交通量时空特性的分析，为智能交通量管理系统的研究奠定了基础。下一步研究，将利用高速公路交通量的时空特性，对交通状态进行研究预测未来时刻交通状态，为人们出行选择提供指导。

［1］李松江，张异，龚跃.基于蚁群算法的智能交通最优路径研究［J］.长春理工大学学报：自然科学版，2015（4）：122-126.

［2］Yuan P C，Lin X X.How long will the traffic flow time series keep efficacious to forecast the future?［J］.Physica A Statistical Mechanics&Its Applications，2017（467）：419-431.

［3］Koesdwiady A，Soua R，Karray F.Improving traffic flow prediction with weather information in connected cars：A Deep Learning Approach［J］.IEEE Transactionson VehicularTechnology，2016，65（12）：9508-9517.

［4］Chen P，Ding C，Lu G，et al.Short-term traffic statesforecasting considering spatial-temporalimpact on an urban expressway［J］.Transportation Research Record：Journd of the Transportation Resarch Board，2016，2594：61-72.

［5］邢雪，于德新，田秀娟，等.基于数据挖掘的高速公路行程时间预测［J］.华中科技大学学报：自然科学版，2016，44（8）：36-40.

［6］Lim S H，Kim Y，Lee C.Real-time travel-time prediction method applying multiple traffic observations［J］.Ksce Journal of Civil Engineering，2016，20（7）：1-8.

［7］罗京，刘建蓓，郭腾峰，等.降雨对高速公路交通流特征的影响［J］.公路交通科技，2015，32（7）：134-139.

［8］沈强儒.高速公路菱形立交关键部位交通量适应性与技术指标研究［D］.西安：长安大学，2016.

［9］杨鹏，陈楠，袁坤.基于综合调查方法下的高速公路交通量分析研究［J］.公路交通科技：应用技术版，2016（4）：304-306.

［10］李宏德.基于运动学的高速公路汽车慢行对交通量的影响分析［J］.河南科学，2013（11）：1863-1865.