3T1R并联机构运动学分析与优化设计
2018-01-17杨桂林吴存存陈庆盈
杨桂林 吴存存 陈庆盈 王 逸 张 驰
(1.中国科学院宁波材料技术与工程研究所, 宁波 315200; 2.浙江省机器人与智能制造装备技术重点实验室, 宁波 315200)
引言
空间四自由度(Degree of freedom,DOF)并联机构特别是能实现SCARA运动(即沿x、y、z轴的平动和绕z轴的转动,也称3T1R运动)的并联机构可广泛应用于分拣、包装、码垛、装配等操作中,其中最普遍的一类是在3-DOF Delta机器人[1]的基础上开发的,它通过在动、定平台之间加装中间支链实现1-DOF的转动。但由于中间支链的可伸缩杆通过一对分离的万向节连接到动、定平台上,很难实现平稳和精确的运动。为了克服这些缺点,一类由定平台、4条支链和双动平台组成的SCARA运动并联机构[2-8]应运而生。不同于传统并联机构动平台的简单刚性结构,这类机构的动平台由2个子平台组成,并通过其相对运动和特别设计的传动装置实现所需的旋转运动。尽管这类SCARA运动并联机构可实现平稳转动,但由于双动平台的存在,导致其结构和运动学都较为复杂。为此,提出了一类具有4条支链和刚性单动平台的SCARA运动并联机构[9-15]。然而,由于运动奇异和支链间的机械干涉,这类机构的工作空间特别是转动范围受限。为了实现更大的转动范围,ANGELES等[16-17]提出一类由动平台、定平台和2条相同的4-DOF混联支链组成的并联机构,但其机械结构较为复杂。
目前这类可实现SCARA运动的单平台并联机构大多采用4条支链、以转动副作为驱动副的形式,在轻小物料中、短距离的高速操作方面表现良好。本文提出4PPa-2PaR并联机构[18](P代表移动副,Pa代表平行四边形机构副,R代表转动副),其采用2条相同支链,以移动副作为驱动副。
1 机构简介
1.1 机构描述
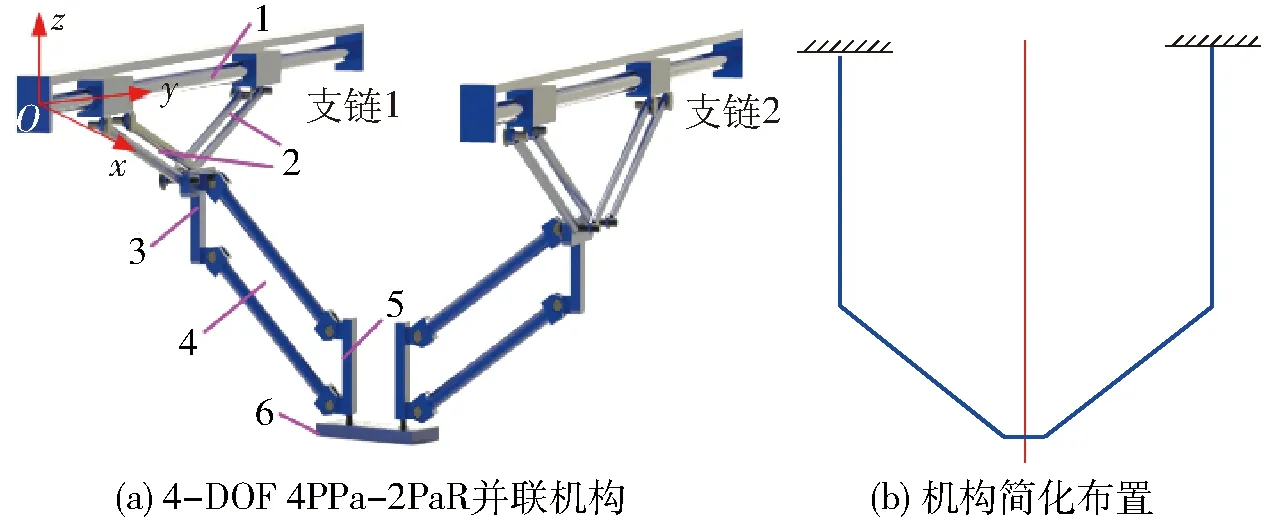
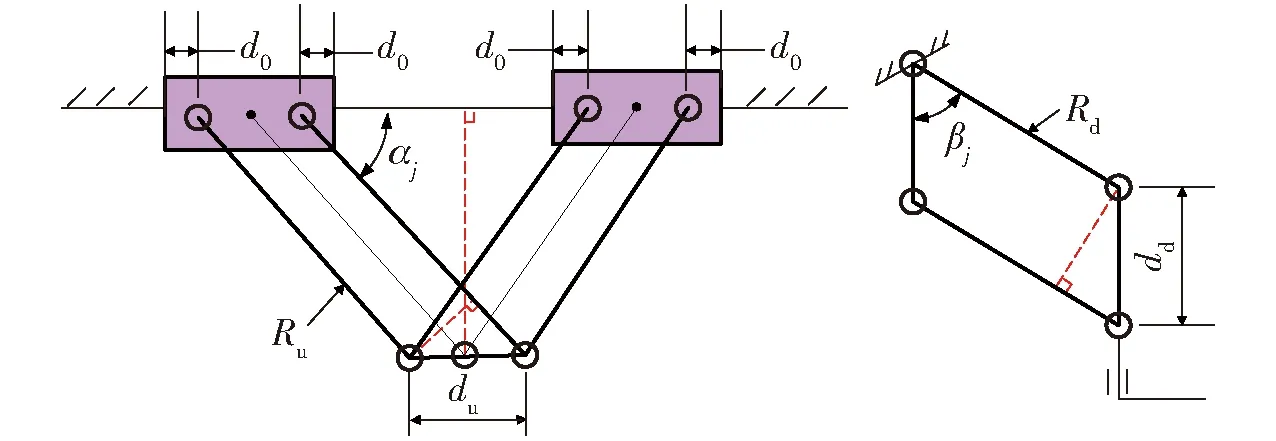
图1 4PPa-2PaR并联机构Fig.1 4PPa-2PaR parallel manipulator1.定平台(导轨) 2.上部平行四边形机构 3.上部连接件 4.下部平行四边形机构 5.下部连接件 6.动平台
4PPa-2PaR并联机构由动平台、定平台和2条相同支链组成,如图1所示。
在每条支链上,主动移动副(P)呈共线布置,安装在定平台上,可利用共用同一定子的2台直线电机驱动。机构中含有由4个同轴转动副(R)构成的闭合回路,即上、下部平行四边形机构。每条支链的上部平行四边形机构刚性地连接到2个移动副(P)上,下部平行四边形机构通过被动转动副(R)垂直地连接到动平台上,因而,每条支链都是具有SCARA运动能力的四自由度运动链,故由2条相同支链支撑的动平台可实现期望的四自由度SCARA运动。
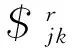

图2 4PPa-2PaR并联机构运动链Fig.2 Kinematic chain of 4PPa-2PaR parallel manipulator

参数含义a/m转动副P1到转动副P2的距离b/m两导轨之间的宽度d/m转动副Dj到动平台的距离L0/m导轨长度lu/m上部平行四边形机构杆长ld/m下部平行四边形机构杆长qi/m主动移动副Bi的位移αj/rad导轨到上部平行四边形机构杆件的角βj/rad下部平行四边形机构杆件CjFj到CjDj的角
建立定坐标系{B}:oxyz(原点位于支链1导轨一侧,y轴沿导轨方向,x轴沿导轨宽度方向,z轴由右手定则确定)和动坐标{E}:px′y′z′(原点位于动平台中心,x′轴由转动副P1指向转动副P2,y′轴过动平台中心,且在动平台所在平面垂直于x′轴,z′轴由右手定则确定)。该并联机构独立的输入参数为(q1,q2,q3,q4),即主动移动副的位置,输出参数为(x,y,z,θ),即动平台的位姿。
1.2 自由度分析
基于螺旋理论分析并联机构自由度的性质,自由度利用修正的G-K公式[19]计算,即
(1)
如图2a所示,该机构第1分支的运动螺旋系可表示为
(2)
对式(2)求反螺旋得第1分支约束螺旋系
(3)
同理,可求得第2分支的约束螺旋系。因此,整个机构的约束螺旋系可求,即包括关于x轴和y轴的4个约束力偶,其形成2个公共约束(λ=2),限制了支链绕x轴和y轴的转动。利用修正G-K式(1)求该机构的自由度为
MN=4(22-26-1)+26+0-2=4
(4)
为了分析动平台4个自由度的性质,可以对机构的约束螺旋系求二次反螺旋,即
(5)
式(5)表明自由度的性质是3个移动运动和1个绕z轴的转动运动。在该机构任何可能的运动过程中,式(2)和式(3)总保持不变,公共约束和冗余约束也保持不变,自由度是全周的。因此,证明4PPa-2PaR并联机构可实现四自由度的SCARA运动。
2 运动学分析
4PPa-2PaR并联机构的运动学分析主要包括位置分析和速度分析两大部分。位置分析的目的是找出主动关节位移和末端执行器姿态之间的运动学关系。
如图2和表1所示,设点Bi、Cj、Dj、Pj相对于定坐标系{B}和点Dj、Pj相对于动坐标系{E}的位置坐标为
(6)
动平台的位置由矢量给出,其转动角度由θ表示。基于提出的4PPa-2PaR并联机构的运动特性,给出动坐标系到定坐标系的变换矩阵TBE为
(7)
2.1 位置正解分析
位置正解是当机构的结构参数和主动关节的位置(q1,q2,q3,q4)已知时,求解末端执行器的姿态(x,y,z,θ)。
由于并联机构闭环约束关系的存在,使得机构的位置正解分析比较困难,不仅涉及求解高次非线性方程,而且具有多种可能解。目前主要的求解方法有解析法[20]和数值法[21-22]。
(8)
动平台上点Pi在动坐标系{E}的坐标为P′1=(-a/2,0,0),P′2=(a/2,0,0)。
利用变换矩阵TBE,可求得点Dj相对于定坐标系{B}的坐标,即
(9)
当并联机构确定时,平行四边形机构的杆长始终保持不变,建立约束方程
(10)
此外,由图2所示投影几何关系可知
(11)
根据式(8)~(11)可求得约束关系
(12)
由式(12)可确定4PPa-2PaR并联机构移动副作为驱动时,机构的位置正解最多存在8组封闭解。
2.2 位置反解分析
位置反解是当机构的结构参数和末端执行器的姿态(x,y,z,θ)已知时求解主动关节的位置(q1,q2,q3,q4)。
4PPa-2PaR并联机构结构简单对称,利用变换矩阵TBE和图2所示几何关系,可求得该机构的位置反解为
(13)

因此可知,4PPa-2PaR并联机构的位置反解易于求解,最多存在4组封闭解。
2.3 位置分析算例
为验证4PPa-2PaR并联机构位置分析的正确性,给出数组机构的位置参数,代入上述并联机构的位置正反解方程中,进行对比验证,检验位置分析结果是否正确。
给出一组4PPa-2PaR并联机构的计算实例,其设计参数为:a=0.2 m,b=0.8 m,lu=0.6 m,ld=0.55 m,L0=2.5 m。特别需要说明的是,为了更好地了解该机构并保证分析的一体性,后续对4PPa-2PaR并联机构工作空间的研究算例同样采用这组设计参数。
取3组动平台在定坐标系{B}中的位姿参数(x,y,z,θ),代入该并联机构的位置反解方程式(13)中,求得主动关节的位置(q1,q2,q3,q4),如表2所示。之后在该表中任取3组位置反解得到的主动关节的位置(q1,q2,q3,q4),作为位置正解方程的输入值,代入式(12),可求得如表3所示的动平台中心点在定坐标系{B}中的位姿(x,y,z,θ)。
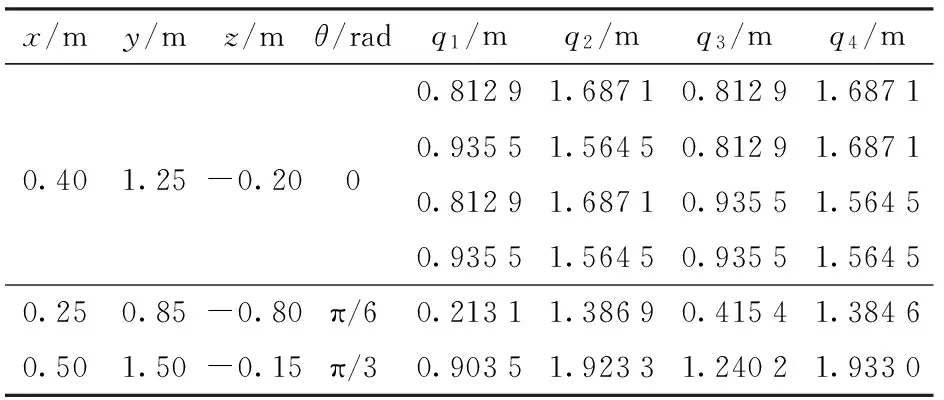
表2 位置反解算例Tab.2 Solutions of inverse displacement
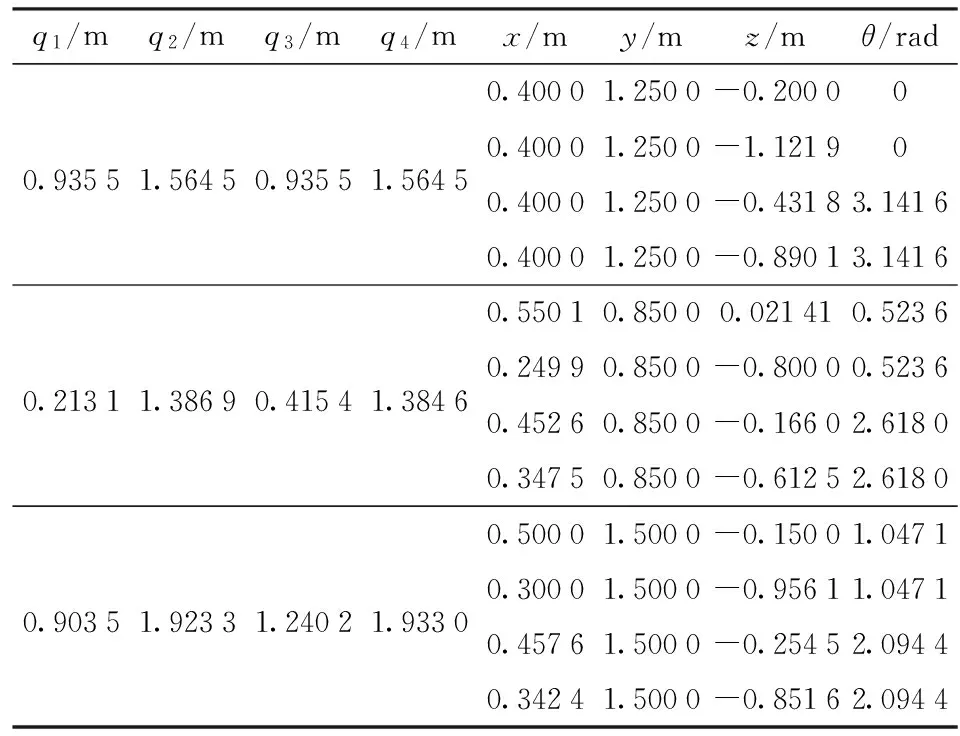
表3 位置正解算例Tab.3 Solutions of forward displacement
通过对比分析,表2、3中的位置正、反解计算结果吻合,验证了4PPa-2PaR并联机构位置分析的正确性。
2.4 速度分析
速度雅可比矩阵通过建立动平台输出和各支链输入之间的速度矢量方程求得,是研究并联机构的基础。
将4PPa-2PaR并联机构位置约束方程式(12)对时间求导,引入参数αj和βj,整理后可求运动输入和运动输出速度之间的关系为
(14)
其中
Jq=
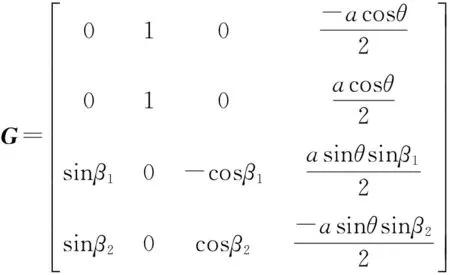

Vp——动平台速度
4PPa-2PaR并联机构的雅可比矩阵Jq和G的行列式为
(15)
2.5 转动能力分析
根据对4PPa-2PaR并联机构的速度雅可比矩阵的行列式式(15)可知,机构的转动范围为[-π/2,π/2]。该并联机构动平台是简单单动平台结构,不含角度放大装置,对具有该类特点的3T1R并联机构的转动能力进行对比,如表4所示。
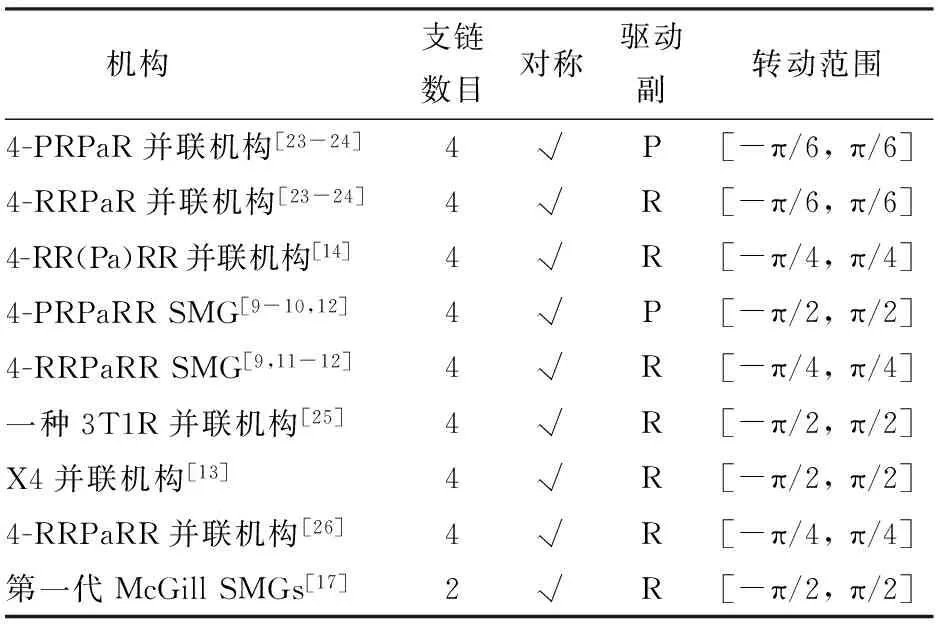
表4 3T1R并联机构对比Tab.4 Comparison of 3T1R parallel manipulator
注:SMG:Schönflies-motion generator,Schönflies运动发生器。
由此可知,目前能实现3T1R运动的单平台对称并联机构,在不存在额外装置来放大转动角度的情况下,最大可达的转动范围为±π/2。此外,目前这类并联机构大多是4条支链、以转动副作为驱动副的形式。
本文提出的4PPa-2PaR并联机构具有2条相同支链,以移动副为驱动副,可通过直线电机驱动。直线电机的行程可通过拼接定子来实现行程的无限扩展,同时可通过在同一定子上配置多个动子来实现同一轴向的多个独立运动控制。沿直线导轨方向的工作空间可无限扩展,这也是该类并联机构最大的特点之一。
3 工作空间分析
并联机构工作空间是评价其运动学性能的重要指标,也是进行尺度参数设计的重要依据[27]。4PPa-2PaR并联机构的工作空间至少需要4个参数描述,为了使工作空间可视化,需要对一个四维工作空间进行降维处理。理论上,对于4PPa-2PaR并联机构,沿y方向的工作空间可无限扩展,可通过固定y,考虑3个维度构成的混合空间,它实际上是xoz平面的平移工作空间和姿态空间的耦合,本文称其为混合空间。
3.1 工作空间确定
对并联机构工作空间的研究主要有数值法和解析法。采用解析法对工作空间分析需要有位置正解的封闭解,虽然4PPa-2PaR并联机构正封闭解存在,但是形式较复杂,因此本文采用数值法研究该机构的工作空间,搜索流程如图3所示,搜索步长根据具体要求选择。
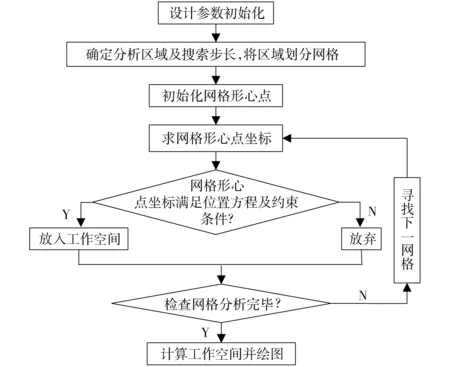
图3 工作空间搜索流程图Fig.3 Flow chart of workspace searching
具体基本思路为:将工作空间区域划分为很多网格,根据机构位置方程和约束条件检查网格形心点是否为可行点,则所有满足要求的可行点构成的区域为工作空间。
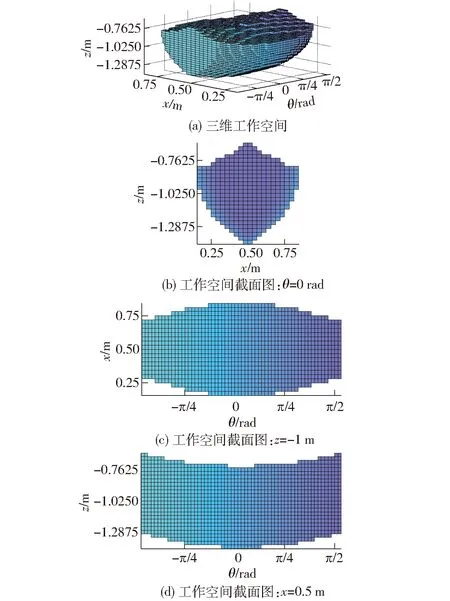
为了更形象地了解4PPa-2PaR并联机构的混合空间,应用上述工作空间搜索方法(图3),给出一组计算实例,其设计参数为:a=0.2 m,b=0.8 m,lu=0.6 m,ld=0.55 m,L0=2.5 m,沿x、z、θ方向各划分32、34和60个网格,其中y=L0/2,d=0.15 m,则可确定该并联机构混合空间如图4所示,大小为0.551 2 m2·rad。

图4 4PPa-2PaR并联机构的工作空间Fig.4 Workspace of 4PPa-2PaR parallel manipulator
3.2 设计参数对工作空间的影响
为了更直观了解各设计参数对机构混合空间的影响,采用单变量法进行分析。对于上述一组计算实例,给定各设计参数的限定范围如表5所示,设计参数对机构混合空间的影响如图5所示。
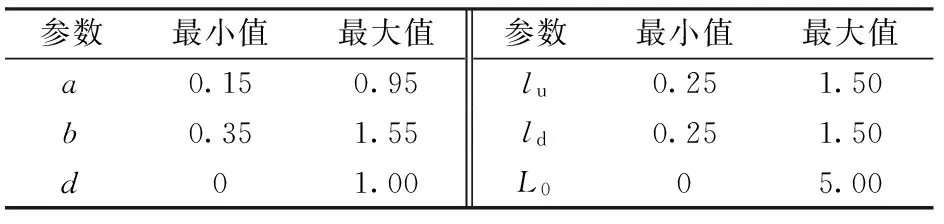
表5 各设计参数的限定范围Tab.5 Range of parameters m
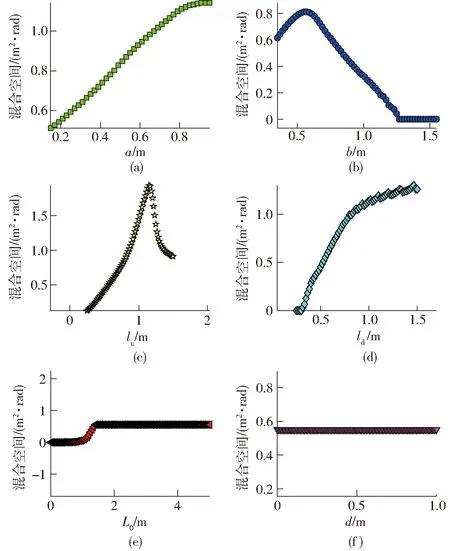
图5 设计参数对工作空间的影响Fig.5 Influence of design parameters on workspace
由图5可知:①设计参数b、lu对4PPa-2PaR并联机构混合空间的影响趋势基本是先增大后减小,呈现非线性特点,如图5b和5c所示。②当混合空间存在时,设计参数a、ld、L0增大,并联机构的混合空间增大,如图5a、5d和5e所示。不同的是:a、ld对工作空间的影响是非线性的;L0对工作空间的影响是线性的,即只要存在混合空间,那么导轨长度L0越大,工作空间越大,因而可根据实际应用需求进行选择。③当参数d在给定区域变化时,并联机构的混合空间几乎没有变化,如图5f所示,故在设计过程中可根据实际情况给定,无需作为设计参数。④除参数d和L0外,其余各设计参数对并联机构混合空间的影响程度不同,如图5所示。其中,lu对混合空间的影响最大,a和ld对混合空间的影响其次,b对混合空间的影响相对较小。⑤当各设计参数满足一定的约束条件时,开始出现工作空间,由4PPa-2PaR并联机构的运动关系可知,需要满足的约束条件为:ld>(b-acosθ)/2。
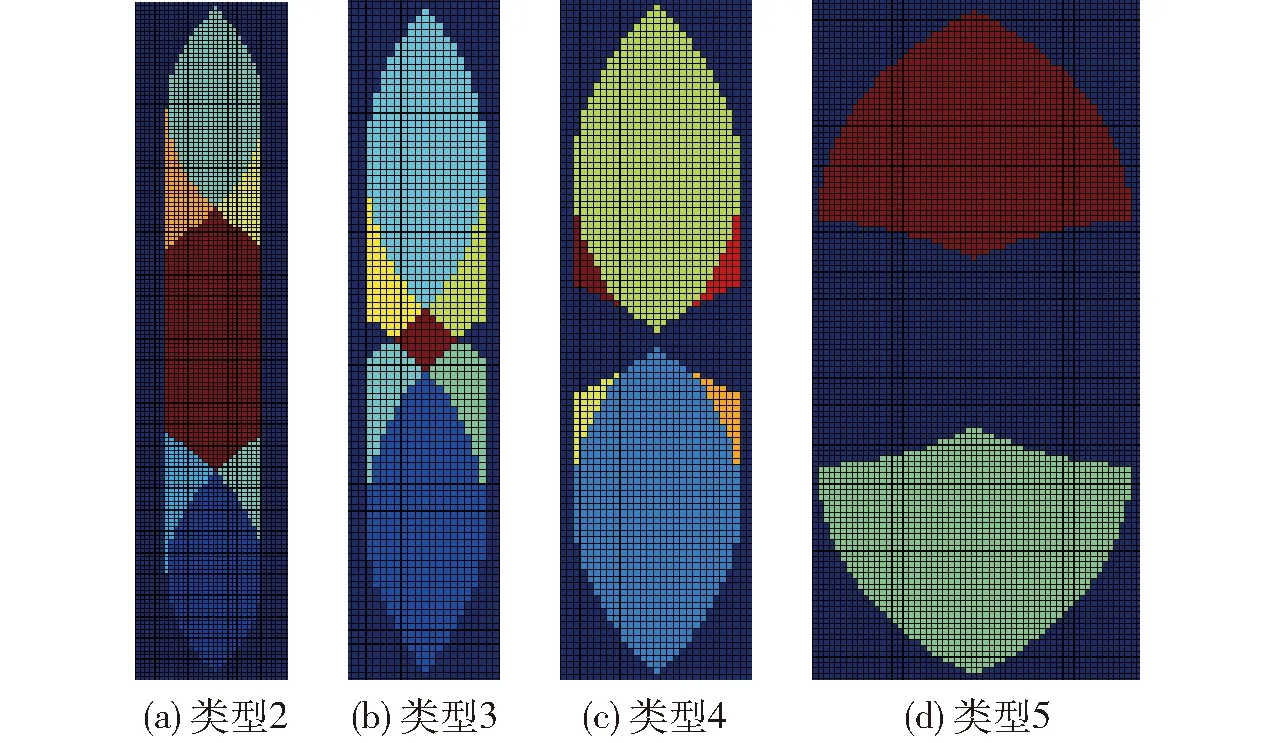
3.3 工作空间形状分析
根据4PPa-2PaR并联机构工作空间在xoz截面的形状及奇异位形的情况,可将工作空间分为如下几种类型:
类型1:当下部平行四边形机构的杆长(即圆的半径)ld满足:0 类型3:当下部平行四边形机构的杆长ld满足: 图6 4PPa-2PaR并联机构工作空间形状Fig.6 Workspace shape of 4PPa-2PaR parallel manipulator 由图6可知:①4PPa-2PaR并联机构如果工作空间存在,则工作空间形状共有4种类型:类型2~类型5。②4PPa-2PaR并联机构的每一种工作空间的形状分布沿x方向关于2条导轨的中心平面对称。③4PPa-2PaR并联机构的每一种工作空间的形状分布沿z方向关于直线z=-lu/2-d对称。 4.1.1确定设计变量 根据前面对4PPa-2PaR并联机构工作空间的分析可知,导轨长度L0和转动副Dj到动平台的距离d可根据具体任务要求给定。考虑到总体设计中已确定的固定参数,要得到一个确定的4PPa-2PaR并联机构主要有4个设计变量,即a、b、lu和ld(图2和表 1)。 4.1.2建立目标函数 在并联机构设计中,在满足约束条件的前提下,通常希望机构结构紧凑、协调性好且具有性能良好的较大工作空间。在考虑4PPa-2PaR并联机构特性的基础上,选择混合空间作为优化目标,其他设计要求作为约束条件处理。对结构完全相同的2个并联机构而言,一般尺寸越大工作空间也越大,可通过尺度变换使目标函数无量纲化。因此,选择可用混合空间的体积占自身体积的比值作为优化目标,即 4.1.3设置约束条件 4.1.3.1边界约束 为了保证在有限空间内并联机构设计方案的可行性并便于优化计算,给出4PPa-2PaR并联机构各设计变量的变化范围 (16) 4.1.3.2不干涉性约束 在4PPa-2PaR并联机构中,平行四边形机构的连杆是有一定物理尺寸的。在机构运动过程中,同一平行四边形机构的两连杆之间可能发生干涉;不同平行四边形机构的连杆也可能发生干涉。后者可通过调整机构布局来避免。为讨论方便,假设各连杆都是质量均匀的圆柱形杆件,Ru和Rd分别表示上、下部平行四边形机构的连杆半径,du和dd分别表示上、下部同一平行四边形机构两连杆中心线之间的最长距离,如图7所示。同一平行四边形机构的两杆不发生干涉,要求两连杆间的距离大于等于两连杆半径之和,即 (17) 图7 4PPa-2PaR并联机构局部结构及尺寸Fig.7 Partial structure and size of 4PPa-2PaR parallel manipulator 4.1.3.3避奇异约束 通过分析动平台和主动关节之间的瞬时速度关系来研究该并联机构的奇异位形。由式(15)可判断4PPa-2PaR机构的奇异位形,为避开奇异位形,需满足的约束条件为: (1)避开αj=0时逆奇异的情况。导轨长度是一定的,对j(j=1,2)支链而言,上部2个平行四边形机构拉开时,最高不能超过导轨所在平面。当到达最高极限位置时,两滑块之间的距离应小于等于导轨长度,即 2lucosαjmin≤L0 (18) (2)避开αj=π/2时逆奇异的情况。上部平行四边形机构的转动副中心距离滑块边界距离为d0(图7)。对j(j=1,2)支链而言,当上部2个平行四边形机构靠近,到达最低极限位置时,两滑块不能相碰,即满足 lucosαjmax≥d0+du/2 (19) (3)避开βj=π/2逆奇异、β1+β2=π正奇异和β1=β2=π/2混合奇异的情况。根据图3所示投影几何关系,当βj=π/2时存在如下等式关系 acosθ+ldsinβ1+ldsinβ2=b (20) 4.1.3.4工作空间形状约束 考虑到4PPa-2PaR并联机构的实际应用场合,选择机构的下部区域运动更合理。受机构实际应用情况和结构稳定性的限制,整个机构的高度不能太高。综合各方面因素,对该机构而言,可选择上下工作空间分离但内部有奇异位形的工作空间(图6c),此时奇异位形位于工作空间区域的上部两侧,“肩部”区域占比很小,通过前面施加避奇异约束条件,此时工作空间的奇异位形是可以避开的;或选择下部无奇异位形的工作空间(图6d)。根据对4PPa-2PaR并联机构的工作空间形状分析可知,需满足约束条件 (21) 优化算法的选择取决于数学模型。根据4PPa-2PaR并联机构的优化模型可知,这是一个非线性的约束优化问题,无论目标函数还是约束条件都比较复杂。为此,本文选择遗传算法(Genetic algorithm,GA)作为优化方法。该方法广泛应用于并联机构的全局优化问题,且不需要目标函数的梯度信息。实践表明,GA解决这类优化问题是简单有效的。 利用Matlab遗传算法工具箱对4PPa-2PaR并联机构进行优化计算,其中GA的参数选择直接影响优化结果。本优化主要的GA参数配置和各设计参数的尺寸约束范围分别如表6和表7所示。 表6 遗传算法参数Tab.6 Parameters of genetic algorithm 表7 设计参数的上下边界Tab.7 Boundary values of design parameters m 利用上述优化数学模型及选择的优化算法对机构进行尺寸优化设计,遗传算法的优化结果如表 8所示,最佳目标函数值随进化代数变化曲线如图8所示,其中Vmechanism=πb(lu+ld)。结果表明,优化后4PPa-2PaR并联机构的工作空间整体体积增加54.43%;工作空间相对于机构自身比重增加1.52%。由此可见,本文建立的数学模型及选择的优化算法是正确、有效的。 表8 遗传算法优化结果Tab.8 Optimal results of genetic algorithm 图8 最佳目标函数值随进化代数变化曲线Fig.8 Changing curves of optimal object function values with generation 考虑到机构的实际加工精度和制造成本,将优化后的设计参数圆整,得到一组机构的优化设计参数为:a=0.3 m,b=1.0 m,lu=0.7 m,ld=0.7 m。 图9表示优化后这组设计参数对应并联机构的工作空间,由此可见,优化后并联机构的工作空间结构紧凑,没有空洞,具有良好的工作能力。该组优化设计参数可为后续4PPa-2PaR并联机器人的样机设计提供参考。 图9 机构优化后的工作空间Fig.9 Workspaces after optimization 以一种可实现SCARA运动的4-DOF并联机构为研究对象,基于螺旋理论验证了4PPa-2PaR并联机构具有4个自由度、可实现3T1R运动。根据机构的运动学特性和构型特点分析了机构的运动学问题,结果表明,该机构位置正解的封闭解最多有8组解,位置反解最多有4组解。利用数值法和解析法研究了机构的工作空间及其形状,分析了机构设计参数对工作空间的影响和工作空间形状的约束条件。以可用混合空间的体积占自身体积的比值为目标函数,设置影响工作空间的约束条件,基于遗传算法对该机构进行了尺寸优化设计。研究表明,该机构工作空间结构紧凑,没有空洞,具有良好的工作能力,且优化后工作空间的体积和工作空间相对于机构自身的比重明显增大,优化结果可为后续4PPa-2PaR并联机器人的样机设计提供参考。 1 CLAVEL R. Device for the movement and positioning of an element in space:U.S. 4,976,582[P].1990-12-11. 2 PIERROT F, COMPANY O. H4: a new family of 4-DOF parallel robots[C]∥Proceedings of the 1999 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, 1999: 508-513. 3 KRUT S, BENOIT M, OTA H, et al. I4: a new parallel mechanism for scara motions[C]∥Proceedings of the 2003 IEEE International Conference on Robotics and Automation, 2003,2:1875-1880. 4 NABAT V, DE LA O RODRIGUEZ M, COMPANY O, et al. Par4: very high speed parallel robot for pick-and-place[C]∥Proceedings of the 2005 IEEE/RSJ International Conference on Intelligent Robots and Systems, 2005: 553-558. 5 KRUT S, COMPANY O, NABAT V, et al. Heli4: a parallel robot for scara motions with a very compact traveling plate and a symmetrical design[C]∥Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems,2006: 1656-1661. 6 PIERROT F, NABAT V, COMPANY O, et al. Optimal design of a 4-DOF parallel manipulator: from academia to industry[J].IEEE Transactions on Robotics, 2009, 25(2): 213-224. 7 LIU S, HUANG T, MEI J, et al. Optimal design of a 4-DOF SCARA type parallel robot using dynamic performance indices and angular constraints[J].Journal of Mechanisms and Robotics, 2012, 4(3): 031005. 8 LI Y H, MA Y, LIU S T, et al. Integrated design of a 4-DOF high-speed pick-and-place parallel robot[J]. CIRP Annals-Manufacturing Technology, 2014, 63(1): 185-188. 9 SALGADO O, ALTUZARRA O, PETUYA V, et al. Synthesis and design of a novel 3T1R fully-parallel manipulator[J].ASME Journal of Mechanical Design, 2008, 130(4): 042305. 10 ALTUZARRA O, HERNANDEZ A, SALGADO O, et al. Multiobjective optimum design of a symmetric parallel schönflies-motion generator[J].ASME Journal of Mechanical Design, 2009, 131(3): 031002. 11 ALTUZARRA O, SANDRU B, PINTO C, et al. A symmetric parallel schönflies-motion manipulator for pick-and-place operations[J].Robotica, 2011, 29(6): 853-862. 12 HERNANDEZ A, ALTUZARRA O, SALGADO O, et al. Designing parallel manipulators: from specifications to a real prototype[J]. Industrial Robot: An International Journal, 2012, 39(5): 500-512. 13 XIE F, LIU X J. Design and development of a high-speed and high-rotation robot with four identical arms and a single platform[J].Journal of Mechanisms and Robotics, 2015, 7(4): 041015. 14 XIE F, LIU X J. Analysis of the kinematic characteristics of a high-speed parallel robot with schönflies motion: mobility, kinematics, and singularity[J].Frontiers of Mechanical Engineering, 2016, 11(2): 135-143. 15 石志新,叶梅燕,罗玉峰,等. 3T1R 并联机构结构设计与位置分析[J/OL].农业机械学报, 2016, 47(8):364-369. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20160848&journal_id=jcsam.DOI:10.6041/j.issn.1000-1298.2016.08.048. SHI Zhixin, YE Meiyan, LUO Yufeng, et al. Structure design and displacement analysis of 3T1R parallel mechanism[J/OL].Transactions of the Chinese Society for Agricultural Machinery,2016,47(8):364-369. (in Chinese) 16 ANGELES J, CARO S, KHAN W, et al. Kinetostatic design of an innovative schönflies-motion generator[J].Proc. IMech E, Part C: Journal of Mechanical Engineering Science, 2006, 220(7): 935-943. 17 GAUTHIER J F, ANGELES J, NOKLEBY S B, et al. The kinetostatic conditioning of two-limb schönflies motion generators[J].Journal of Mechanisms and Robotics, 2009, 1(1): 011010. 18 WU C C, YANG G L, CHEN Q Y, et al. Kinematic design of a novel 4-DOF parallel manipulator[C]∥IEEE International Conference on Robotics and Automation, Singapore, 2017:6099-6104. 19 MERLET J P. Parallel robots[M].Dordrecht:Springer Science & Business Media, 2012. 20 程世利,吴洪涛,姚裕,等.6-SPS并联机构运动学正解的一种解析化方法[J].机械工程学报,2010,46(9):26-31. CHENG Shili, WU Hongtao,YAO Yu, et al. An analytical method for the forward kinematics analysis of 6-SPS parallel mechanisms[J].Journal of Mechanical Engineering, 2010,46(9):26-31.(in Chinese) 21 杨辉,郝丽娜,项超群. 并联机构正运动学 AWPSO-SM 求解算法[J/OL].农业机械学报, 2017,48(1):346-352,412. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20170146&journal_id=jcsam.DOI:10.6041/j.issn.1000-1298.2017.01.046. YANG Hui, HAO Li’na, XIANG Chaoqun. AWPSO-SM algorithm for parallel mechanism forward kinematics[J/OL]. Transactions of the Chinese Society for Agricultural Machinery,2017,48(1):346-352,412. (in Chinese) 22 吴小勇,谢志江,宋代平,等.基于改进蚁群算法的3-PPR并联机构位置正解研究[J/OL].农业机械学报,2015,46(7):339-344. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20150748&journal_id=jcsam.DOI:10.6041/j.issn.1000-1298.2015.07.048. WU Xiaoyong, XIE Zhijiang, SONG Daiping, et al. Forward kinematics of 3-PPR parallel mechanism based on improved ant colony algorithm[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2015,46(7):339-344. (in Chinese) 23 LI Z, LOU Y, LI Z. Type synthesis and kinematic analysis of a new class schönflies motion parallel manipulator[C]∥IEEE International Conference on Information and Automation, 2011: 267-272. 24 LI Z, LOU Y, ZHANG Y, et al. Type synthesis, kinematic analysis, and optimal design of a novel class of schönflies-motion parallel manipulators[J].IEEE Transactions on Automation Science & Engineering, 2013, 10(3):674-686. 25 KIM S M, KIM W, YI B J. Kinematic analysis and optimal design of a 3T1R type parallel mechanism[C]∥IEEE International Conference on Robotics and Automation, 2009:2199-2204. 26 WU G, BAI S, HJORNET P. Design analysis and dynamic modeling of a high-speed 3T1R pick-and-place parallel robot[M]∥Recent Advances in Mechanism Design for Robotics. Berlin: Springer International Publishing, 2015:285-295. 27 黄真,刘婧芳,李艳文.论机构自由度:寻找了150年的自由度通用公式[M].北京:科学出版社,2011:4-119.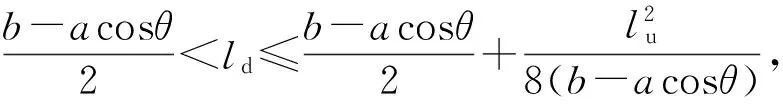
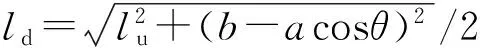
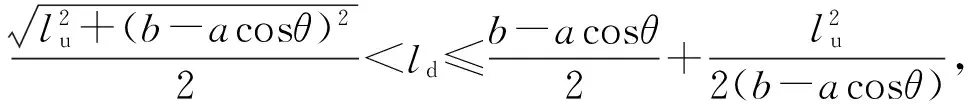
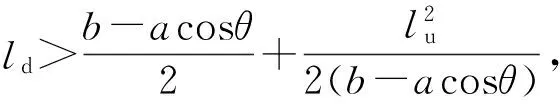
4 优化设计
4.1 建立数学模型
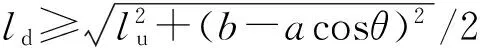
4.2 选择优化算法
4.3 优化算例



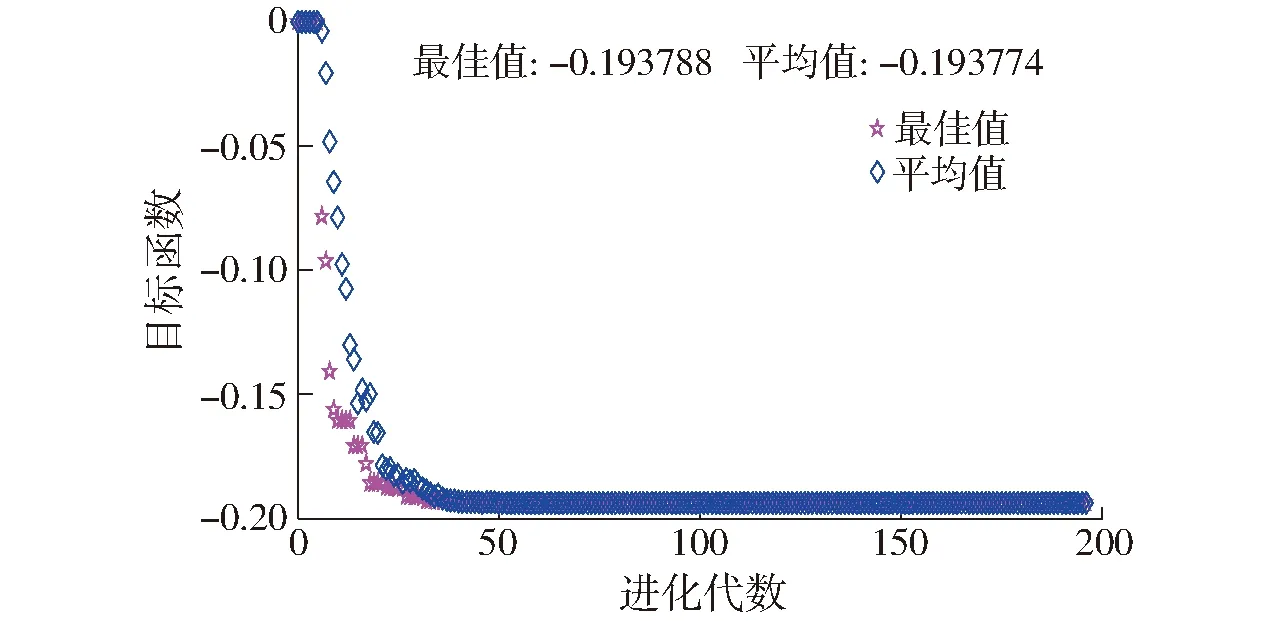
5 结束语
