多点源滴灌条件下红壤水分溶质运移试验与数值模拟

裴青宝 刘伟佳 张建丰 王海伟

(1.西安理工大学水利水电学院， 西安 710048； 2.南昌工程学院江西省水工程安全与资源高效利用工程研究中心， 南昌 330099；3.江西省水利规划设计院， 南昌 330020)

引言

南方红壤丘陵地区多种植柑橘、脐橙等经济作物，近年来在丘陵地区这些作物的灌溉多采用滴灌水肥一体化灌溉方式，本文根据对柑橘、脐橙等作物根系的调查和红壤剖面土壤容重的测定，通过试验研究不同滴头流量、间距以及土壤容重下交汇入渗规律以及土壤水分氮素分布特性，以期为红壤柑橘、脐橙滴灌设计参数选择提供依据。

1 材料与方法

1.1 供试土壤

试验土壤于2016年3月采自江西省寻乌县澄江镇汶口村脐橙果园内，取地表100 cm的种植土，土壤容重在1.36～1.41 g/cm3之间，将试验土样取回，于试验室风干、过2 mm筛、通风保存,土壤颗粒分析用马尔文激光粒度仪测定，粒径0～0.002 mm、 0.002～0.02 mm、 0.02～2 mm之间的颗粒含量分别为44.25%、38.39%、17.36%，采用国际制土壤质地分级标准，最终确定土壤质地为壤质粘土。试验在南昌工程学院灌溉排水实验中心展开，时间为2016年6—12月，室内温度保持为18～23℃。

1.2 试验装置

试验装置采用西安理工大学水资源所设计生产的土壤水分运动试验系统，系统由马氏瓶、有机玻璃土箱、支架等组成；土箱设计为矩形结构，长×宽×高为40 cm×40 cm×60 cm。土壤含水率的测量采用埋设在土体内不同深度处的TDR探头测定，TDR探头2组共13个，分别在1号滴头水平距离为5 cm,垂直距离为5、10、15、20、25、30 cm处和在湿润锋交汇面水平距离为20 cm，垂直距离为0、5、10、15、20、25、30 cm处埋设TDR探头，记录不同时间点的土壤含水率，其他位置通过烘干法测定。Hydrus-3D建模过程中与物理模型相应的位置插入观测点，采用马氏瓶供水，医用针头模拟滴灌出水，用流量计控制流量。装置示意图如图1所示。

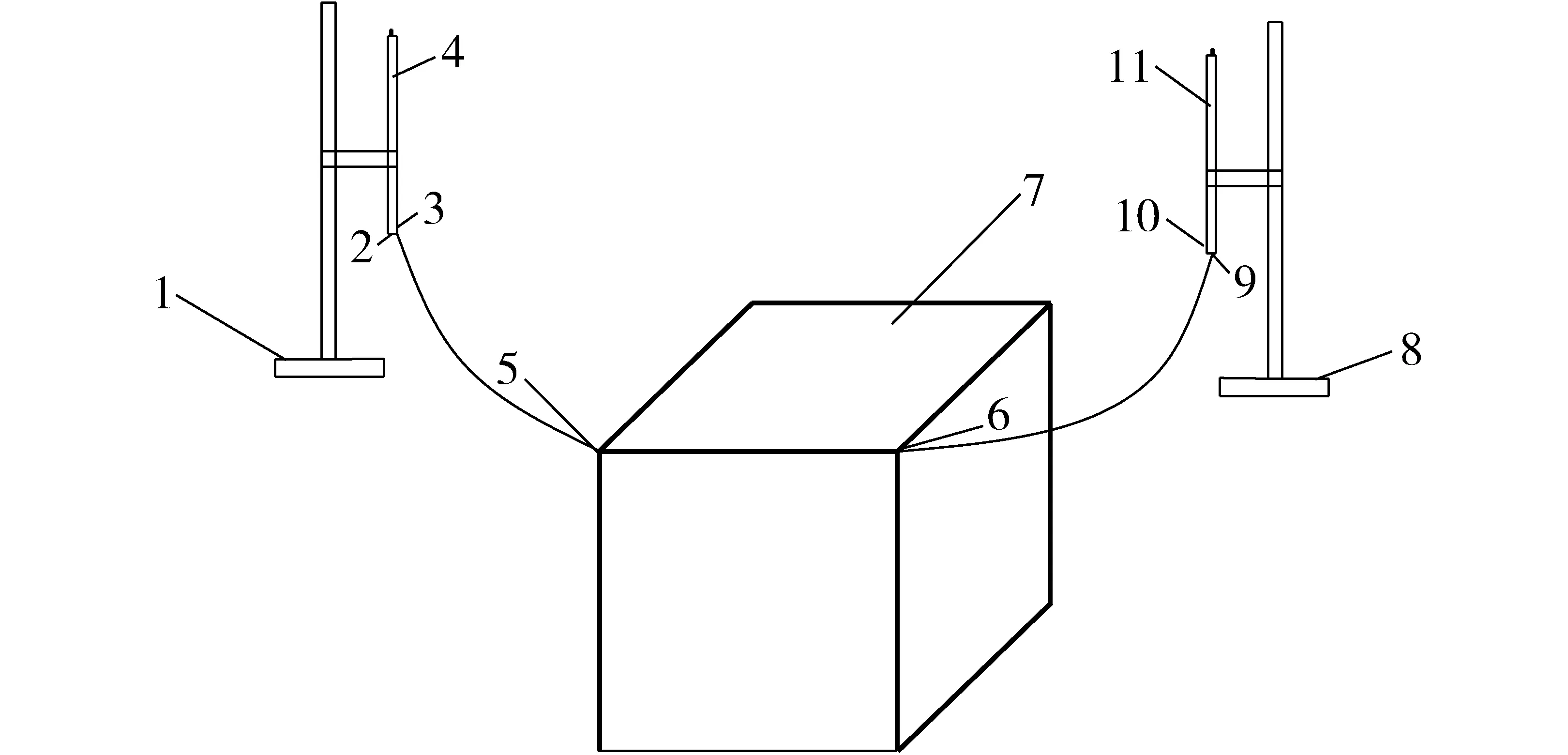
图1 试验装置示意图Fig.1 Sketch of experimental setup1、8.支架 2、9.出水口 3、10.进气口 4、11.马氏瓶 5.1号滴头 6.2号滴头 7.土箱

1.3 试验内容

1.4 试验过程

1.5 数学模型

1.5.1水分运动基本方程

滴灌土壤水分运动为三维流动问题。假定土壤各向同性,地表没有蒸发,土壤初始含水率相同,并不考虑滞后现象,则三维轴对称点源水分入渗Richard方程可表示为[14,17]

(1)

式中θ——土壤体积含水率，cm3/cm3

h——土壤负压水头，cm

r、y、z——坐标(z坐标向下为正)，cm

t——时间，min

Kh——土壤非饱和导水率，cm/min

Hydrus-3D模拟时需要的非饱和土壤水分特征曲线θh、土壤非饱和导水率Kh采用van Genuchten模型表示[14,18]，并不考虑滞后效应

(2)

θh=θs(h≥0)

(3)

(4)

其中

(5)

式中θs、θr——土壤饱和含水率和残余含水率，cm3/cm3

Ks——土壤饱和导水率，cm/min

l——孔隙连通性参数，对大多数土壤来说可取0.5

a、n、m——拟合经验参数

Se——有效含水率(饱和度)

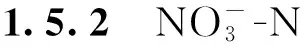
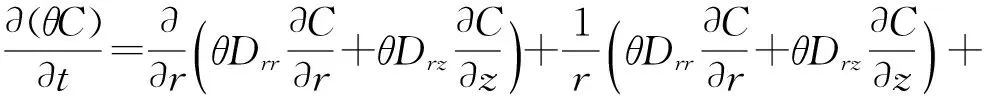
(6)

其中

(7)

(8)

(9)

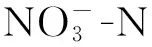
qr——纵向上的土壤水分通量

qz——横向上的土壤水分通量

Drr、Dzz、Drz——水动力弥散系数张量的分量

q——土壤水通量的绝对值

DL、DT——溶质的纵向和横向弥散度，L

Dw——自由水中的分子扩散系数

τ——溶质的弯曲系数，通常表示为土壤体积含水率的函数

1.6 模型区域以及边界条件和初始条件

模型求解区域以实际土箱尺寸为基础建立几何模型，建模区域如图2所示，Hydrus-3D 不能描述移动的水分边界,但可以模拟边界条件随时间变化的过程，因此在试验过程中测定滴头下方积水的区域及水头高度。试验开始后15 min时达到饱和区域的58%、积水深度为0.18 cm(用游标卡尺通过测量滴头下方积水深度得到);灌水后25 min达到饱和区域的80%、积水深度为0.50 cm;38 min 后，饱和区稳定, 积水深度为0.85 cm。根据试验测试结果，饱和区域在很短的时间内达到稳定，所以在模拟过程中不考虑其范围的变化，只输入最终的范围值，设定饱和区半径为定值Rs(滴头地表最小湿润半径)如图2所示。试验过程中无表面蒸发，则水分运动的上边界条件可以表示为

h=0.85 cm (0≤r≤R,z=Z,t≥0)

(10)

(11)

式中R、Z——模拟区域边界(装置物理边界)在径向和垂直方向的坐标

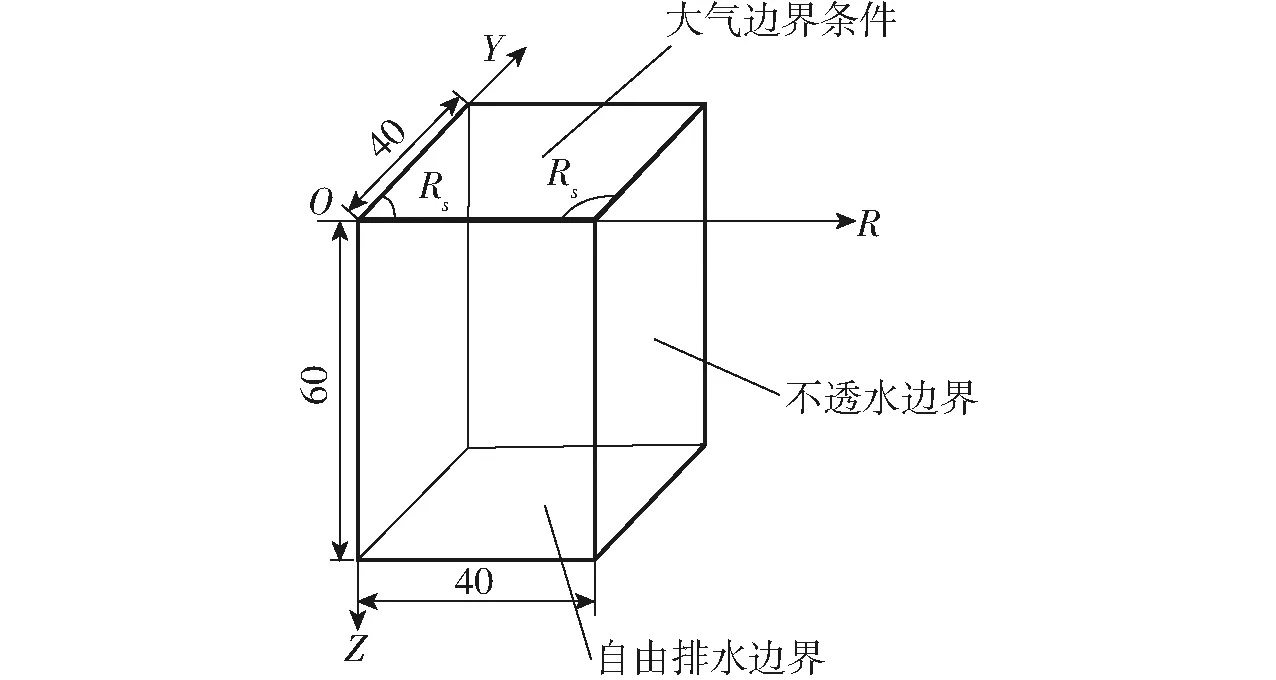
图2 模型求解区域示意图Fig.2 Schematic diagram of solving model

本次模拟输入边界条件中水头随时间的变化个数为4，按照变化的时间，在各段时间上输入相应的水头值。由于滴头周围有积水产生,因此溶质运移的上边界条件采用一类边界条件

C(r,z)=Ca(0≤r≤Rs,z=Z,t>0)

(12)

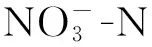
侧面为不透水边界

(13)

(14)

下边界为自由排水边界

(15)

(16)

θ(r,z)=θ0(0≤r≤R,0≤z≤Z,t=0)

(17)

C(r,z)=C0(0≤r≤R,0≤z≤Z,t=0)

(18)

式中θ0——土壤初始含水率，cm3/cm3

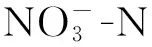
2 模型参数

2.1 土壤水力学参数

依据1.5.1节所述土壤水分特性的 VG 模型参数，结合不同容重的水分特征曲线以及饱和导水率试验结果，并根据颗粒分析的成果输入Hydrus-3D里计算结果并进行对比分析，最终确定合适的参数如表1所示。

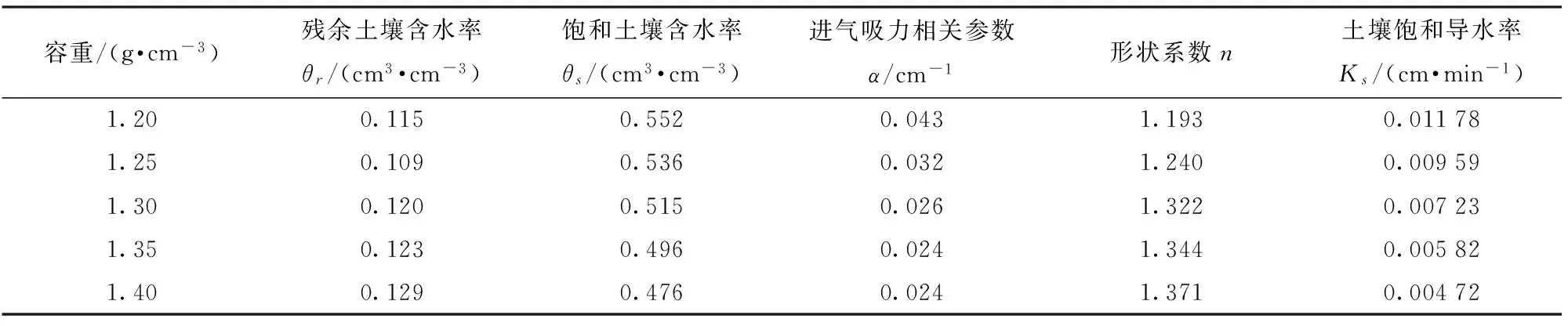
表1 不同红壤容重van Genuchten模型参数Tab.1 Van Genuchten model parameters of red soil with different bulk densities

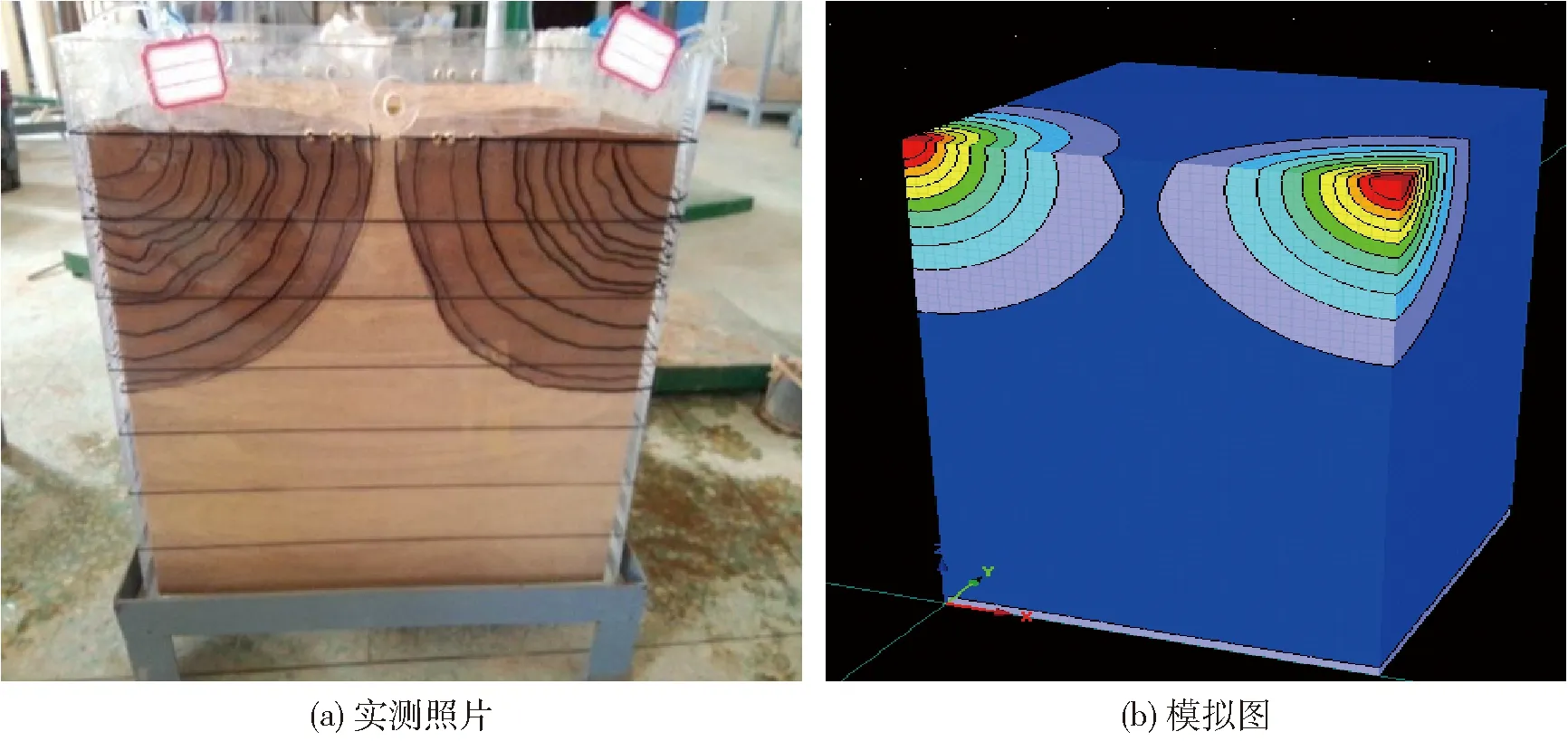
图3 滴灌交汇入渗湿润锋运移变化Fig.3 Changes of drip irrigation, intersection infiltration and wetting front transport

2.2 溶质运移参数

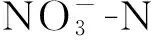
3 结果与分析

3.1 容重变化影响下湿润锋模拟值与试验值的对比分析

试验开始后在滴头下方形成一个积水区域，随着时间的变化，积水区域趋于稳定。水氮开始在土壤中运动，将不同时刻湿润锋的变化在有机玻璃板上用记号笔绘出。图3为滴灌交汇入渗试验湿润锋变化过程实测及模拟照片。

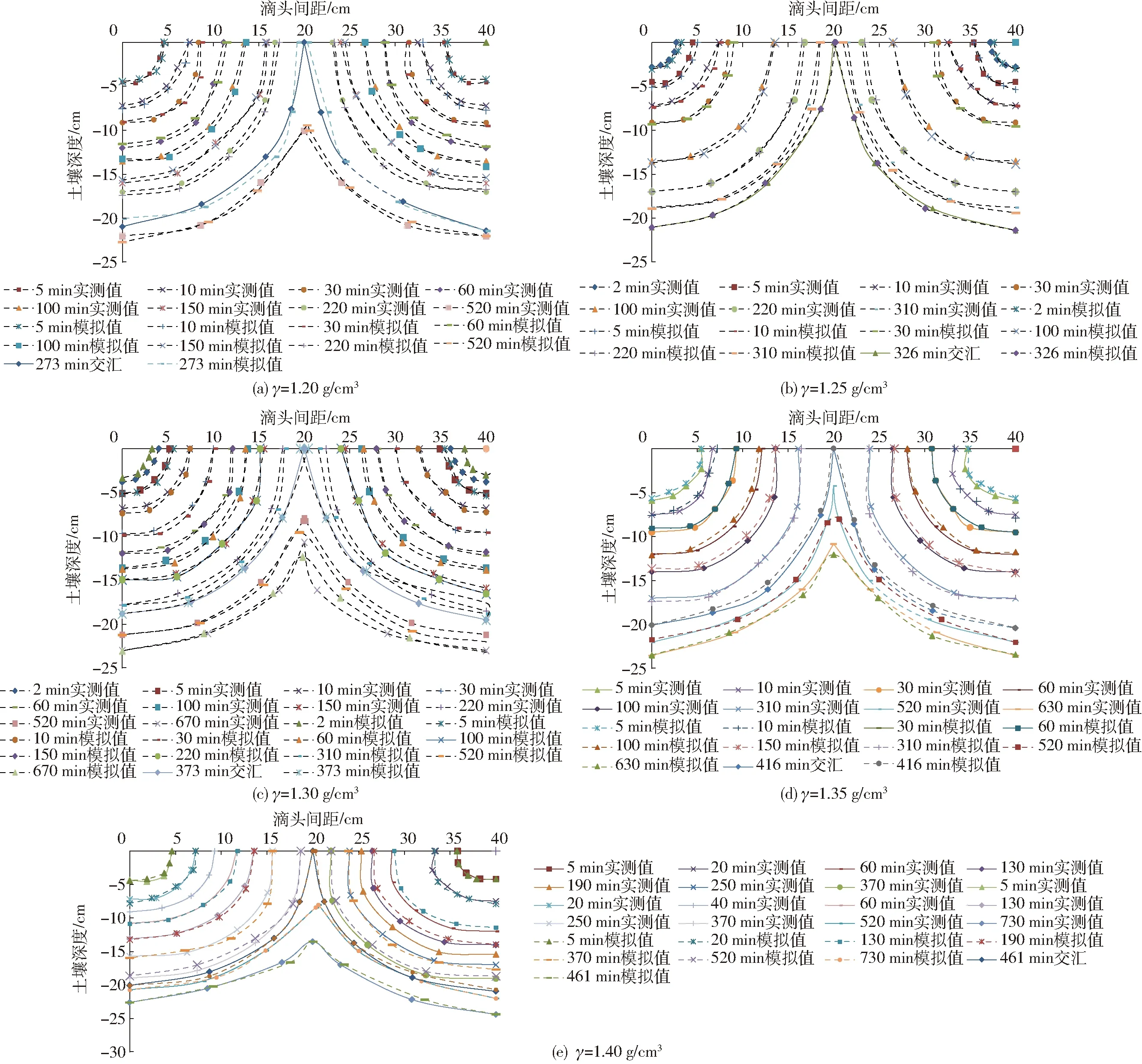
图4 不同容重条件下湿润锋变化模拟值与实测值Fig.4 Simulated and measured values of wetting front under different bulk densities

容重变化影响下湿润锋模拟值与试验值如图4所示(图中γ表示容重)。由图4可见，通过试验测得的湿润锋过程和Hydrus-3D模拟的值在观测时间点上有同步性，其相对偏差在9%以内。5个不同容重的湿润锋模拟值和实测值经过显著性检验后差异均不显著，这说明数值模拟可以反映不同容重条件下湿润锋的运移规律，这也与李久生等[14]、张林等[18]的研究结果相同。模拟的湿润锋以滴头为中心扩散，湿润半径更为圆滑均匀，从图3b的模拟图也可以看出这个现象，而实测的湿润锋某一时刻湿润锋面值则出现凹凸现象；分析认为Hydrus在设定不同的容重后软件认为土壤内部是均一的各向同性，且不受边壁滞后效应的影响。所以Hydrus-3D模拟的湿润锋面推进较快且均匀，而实测值由于土壤为扰动土，装土的质量和土层的结合等情况影响着湿润锋的运移；所以实际工作中如果需要采用模型来预测湿润锋的运移时需要考虑到滞后效应。容重从1.2 g/cm3到1.4 g/cm3，双滴头滴灌下出现了湿润锋的交汇现象，而交汇的时间则与容重有关，容重为1.2 g/cm3的湿润锋在灌水后273 min时发生交汇，而容重越大交汇过程越缓慢，容重1.4 g/cm3在461 min时才发生交汇。试验土为红壤，容重较小时土壤中的孔隙率大，导水速率快，所以湿润锋推进得比较快。当容重增加时，孔隙率减少，加上红壤遇水后颗粒变得粘稠，堵塞了土壤中的孔隙，造成湿润锋不能推进。试验取土的江西省赣州市寻乌县脐橙果园内，现场调查其距地表100 cm以内的土壤容重在1.36～1.41 g/cm3之间，根据模拟和实测结果可知，高容重情况下土壤湿润锋难以推进，交汇发生较缓慢，影响到脐橙的灌溉。所以在灌溉之前需要对土壤结构进行前期处理，疏松土层，便于水肥能够入渗到根系周围。

3.2 湿润体内土壤含水率的分布模拟

结合图5、6土壤含水率模拟和实测值，两者的平均相对误差为9.5%以内。其中，90%的时间节点上的模拟值和实测值的差值在3.5%之内，而且各观测点误差情况类似。差异较大主要在初始时刻和试验结束时段，初始观测点上实测的含水率值均低于模拟值；实测值通过埋设在观测点上的TDR探头测定，探头在使用之前设置在不同的土壤容重中，在灌水后通过与烘干法进行含水率测定率定，并对探头进行修正。所以在试验过程中探头的值可以反映出实际情况，而模拟值出现的偏差主要是在建模过程中模型为理想状态，输入颗分数据和土壤吸力后神经网络预测出一个含水率值，从而造成与实际土壤初始含水率之间的误差。而在灌水结束时出现的部分实测值大于模拟值的原因是，模型在该时刻模拟结束，含水率定格在这个状态，不会变化，模型忽视了土壤水分再分布这一过程，所以实测值大于模拟值。除此之外，模型模拟的精度较高，可以反映出滴灌交汇入渗过程中湿润体内土壤含水率的分布情况，这与李久生等[14-15]的研究结果相同。

图5 不同容重条件下距离滴头5 cm处含水率变化Fig.5 Changes of water content under condition of different densities with 5 cm away from emitter

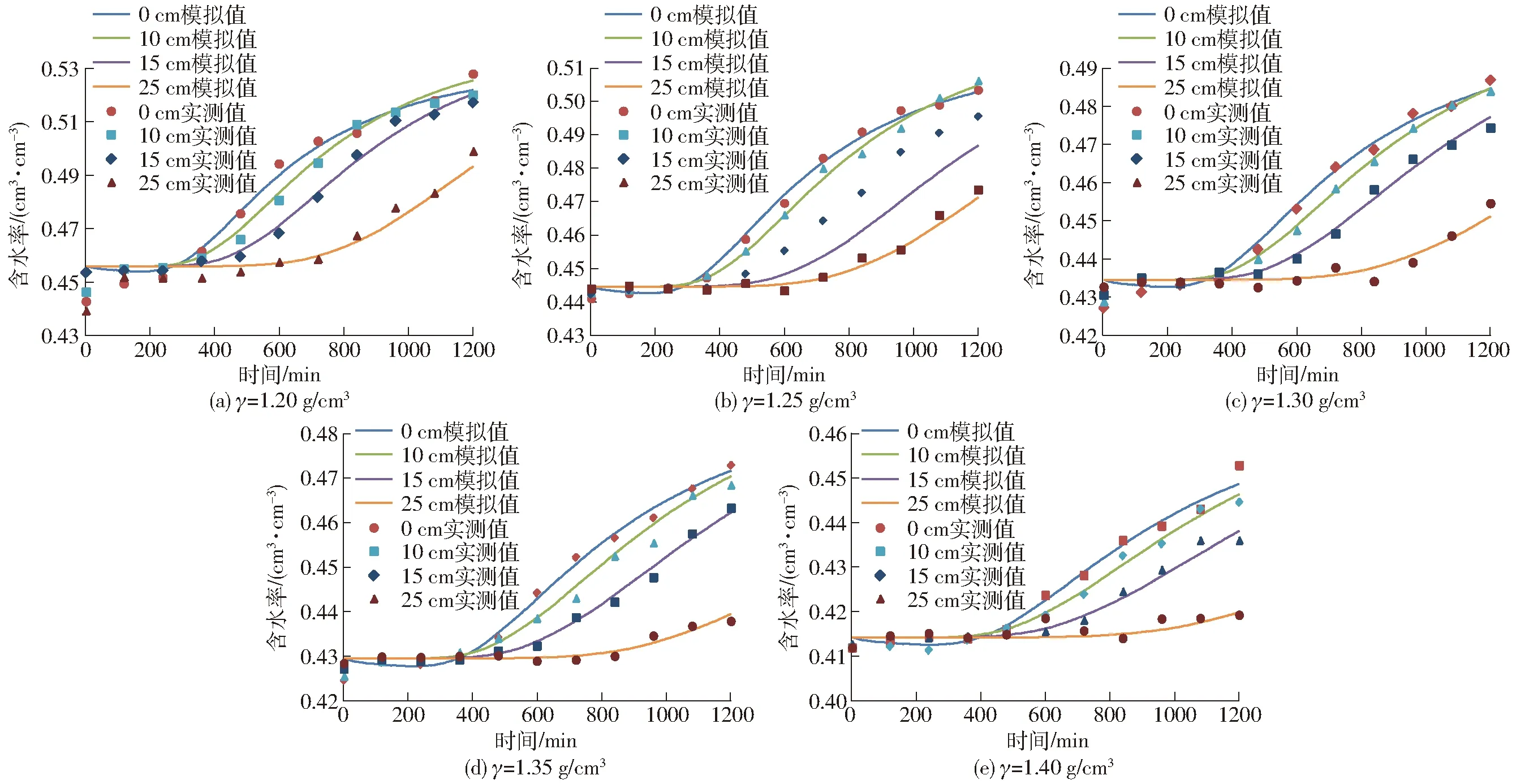
图6 不同容重条件下交汇处含水率模拟值与实测值Fig.6 Confluence of moisture content of simulated and measured values under condition of different densities

图5中，总体而言，随着入渗时间变化，观测点的土壤含水率呈现增加的现象，土壤深度越深，含水率增加值越小。容重1.2 g/cm3垂直距离5 cm的观测点土壤含水率在入渗开始后就快速增加，200 min后接近饱和，并维持稳定状态；其他4个不同容重该位置处的观测点模拟和实测值均显示该现象。其余观测点随着深度的增加，距离滴头间距越大含水率越小，并受到容重的影响，同一位置处的观测点，容重越大，含水率相应地减小，这表明，高容重壤土阻碍了水分的入渗。

图6中交汇处的土壤含水率，在发生交汇后迅速增加，并与深度和容重有关，深度较深容重较大，含水率增加的值较小。交汇面处含水率低于同一位置处滴头下方的观测点的值，由此可知在湿润体内同一深度处，含水率的分布是不均匀的，滴头下方处土壤含水率高于交汇处的，容重越大这一现象愈加明显。对于脐橙等根系发达的经济作物，在滴头间距相同时，两滴头交汇处的土壤含水率较低，会影响这一区域内根系吸水，要加强交汇区域的灌水量。

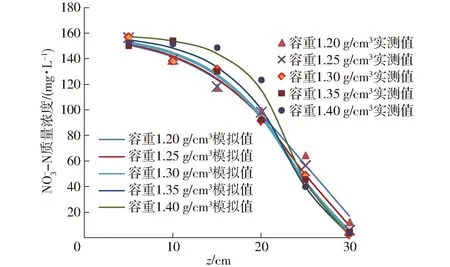
图7 不同容重条件下距离滴头5 cm处质量浓度模拟值与实测值Fig.7 N-N mass concentration simulated and measured values with 5 cm away from emitter under different bulk densities

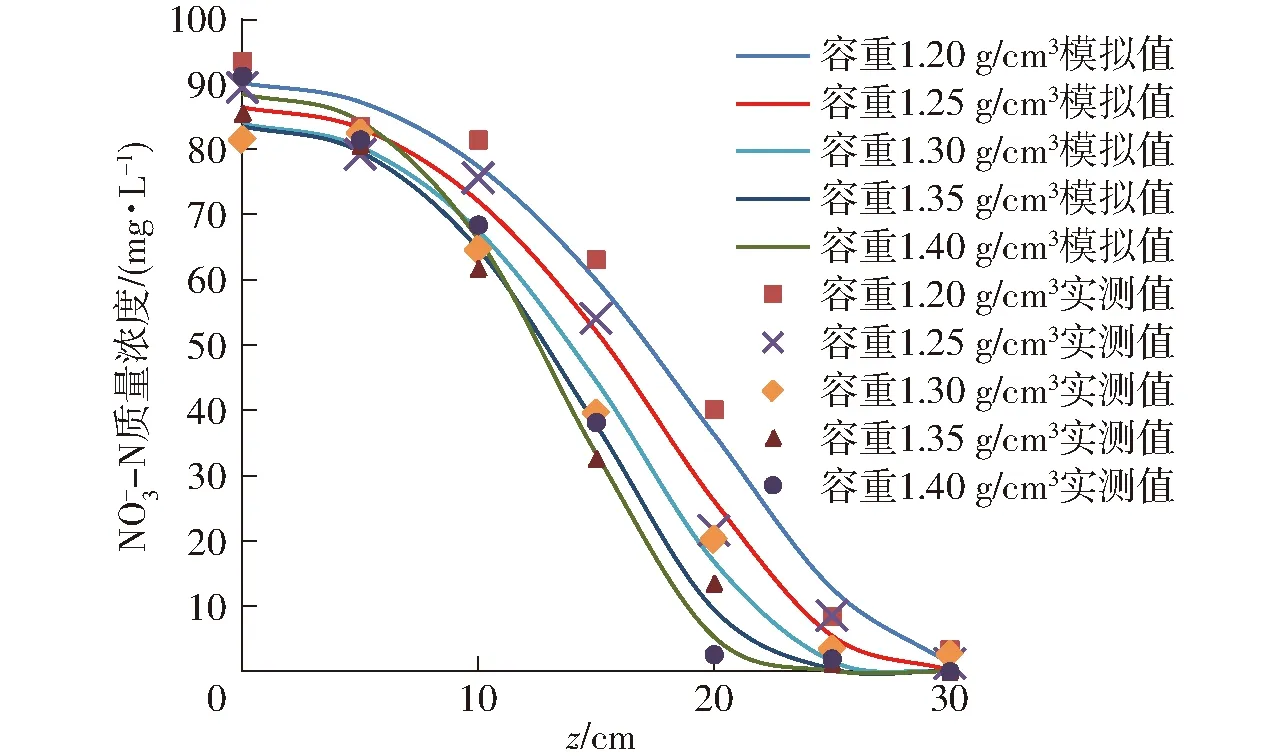
图8 不同容重条件下交汇处质量浓度模拟值与实测值Fig.8 N-N simulated and measured values under different bulk densities intersection

4 结论

(1)Hydrus-3D可以较好地模拟出湿润锋的推移过程，模拟值与实测值的精度在9%以内，软件的模拟值更加理想化，在运用到实际中模拟湿润体范围时需要考虑红壤的空间差异性。

(2)含水率的模拟值和实测值具有很高的一致性，模型可以用于交汇情况下土壤湿润体内含水率分布的模拟。容重对含水率的分布产生较大的影响，交汇面处的含水率低于同一深度滴头下方的值，模拟和实测结果均表明，高红壤容重阻碍湿润锋的推进和含水率的增加。

1 CHARLES M B. Rapid field evaluation of drip and microspray distribution uniformity[J]. Irrigation and Drainage Systems, 2004, 18(4): 275-297.

2 ZHOU Jianbin，XI Jingen，LI Shengxiu. Leaching and transformation of nitrogen fertilizers in soil after application of N with irrigation: a soil column method[J].Pedosphere,2006,16(2):245-252.

3 YANG Lijuan, ZHANG Yulong, XU Hui, et al. Effect of irrigation methods on soil water loss and water use efficiency of tomato in greenhouse[J]. Journal of Irrigation and Drainage, 2004, 23(3): 49-51.

4 李就好，谭颖，张志斌，等.滴灌条件下砖红壤水分运动试验研究[J]. 农业工程学报，2005，21(6)：36-39.

LI Jiuhao, TAN Ying, ZHANG Zhibin, et al. Experimental study on water movement of latosol under drip irrigation[J].Transactions of the CSAE, 2005, 21(6): 36-39.(in Chinese)

5 李凭峰,谭煌,王嘉航,等.滴灌水肥条件对樱桃产量、品质和土壤理化性质的影响[J/OL]．农业机械学报，2017,48(7):236-246．http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20170730&flag=1&journal_id=jcsam.DOI:10.6041/j.issn.1000 1298.2017.07.030.

LI Pingfeng, TAN Huang, WANG Jiahang, et al. Effect of water and fertilizer conditions under drip irrigation on yield, quality of Cherry and physic-chemical properties of soil [J/OL].Transactions of the Chinese Society for Agricultural Machinery，2017,48(7): 236-246． (in Chinese)

6 孙海燕, 李明思, 王振华,等.滴灌点源入渗湿润锋影响因子的研究[J]. 灌溉排水学报，2004,23(3):14-18.

SUN Haiyan，LI Mingsi，WANG Zhenhua, et al. Influence factors on soil wetting front under point drip irrigation [J].Journal of Irrigation and Drainage,2004,23(3):14-18. (in Chinese)

7 张振华,蔡焕杰,郭永昌,等.滴灌土壤湿润体影响因素的实验研究[J].农业工程学报,2002,18(2):17-20.

ZHANG Zhenhua, CAI Huanjie, GUO Yongchang, et al. Experimental study on factors effecting soil wetted volume of clay loam under drip irrigation[J]. Transactions of the CSAE,2002, 18(2): 17-20. (in Chinese)

8 关红杰,李久生, 栗岩峰．干旱区滴灌均匀系数对土壤水氮分布影响模拟[J/OL]．农业机械学报，2014,45(3):107-113．http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20140319&journal_id=jcsam.DOI:10.6041/j.issn.1000-1298.2014.03.019.

GUAN Hongjie, LI Jiusheng, LI Yanfeng. Modeling distributions of water and nitrate in soil as affected by drip system uniformity under arid conditions[J/OL]．Transactions of the Chinese Society for Agricultural Machinery，2014,45(3):107-113． (in Chinese)

9 BRANT A, BRESLER E, DINER N, et al.Infiltration from a trickle source：I. mathematical models[J].Soil Sciences Society of America Proceedings, 1971, 35:675-682.

10 SINGH D K, RAIPUT T B S, SINGH D K, et al. Simulation of soil wetting pattern with subsurface drip irrigation from line source[J]. Agricultural Water Management, 2006, 83(1): 130-134.

11 许迪，程先军．地下滴灌土壤水分运动和溶质运移数学模型的应用[J]．农业工程学报，2002，18(1)：27-31．

XU Di, CHENG Xianjun. Mathematical model for simulating water flow and solute transport during non-steady diffusion from subsurface trickle source[J].Transactions of the CSAE,2002，18(1)：27-31． (in Chinese)

12 李光永,曾德超,郑耀泉. 地表点源滴灌土壤水运动的动力学模型与数值模拟[ J]. 水利学报, 1998, 29(11): 21-25.

LI Guangyong, ZENG Dechao, ZHENG Yaoquan. The mathematical model of water movement from a surface trickle source[J]. Journal of Hydraulic Engineering, 1998,29(11): 21-25. (in Chinese)

13 COTEC M,BRISTOW K L, CHARLES W P B, et al. Analysis of soil wetting and solute transport in subsurface trickle irrigation[J]. Irrigation Science, 2003, 22(3-4): 143-156.

14 李久生，张建君，饶敏杰．滴灌施肥灌溉的水氮运移数学模拟及试验验证[J]．水利学报，2005，36(8)：932-938．

LI Jiusheng, ZHANG Jianjun, RAO Minjie. Model verification of water and nitrate transport from a surface point source[J].Journal of Hydraulic Engineering, 2005, 36(8): 932-938. (in Chinese)

15 陈若男，王全九，杨艳芬. 新疆砾石地葡萄滴灌带合理设计及布设参数的数值分析[J]. 农业工程学报，2010，26(12)：40-46.

16 黄凯，蔡德所，潘伟，等.广西赤红壤甘蔗田间滴灌带合理布设参数确定[J].农业工程学报，2015，31(11)：136-139.

HUANG Kai, CAI Desuo,PAN Wei, et al. Determination of drip tapes layout parameters for irrigation of sugarcane in latosolic red Autonomous Region[J]. Transactions of the CSAE,2015,31(11)：136-139. (in Chinese)

17 RICHARDS L A. Capillary conduction of liquids through porous mediums[J]. Physics, 1931, 1(5): 318-333.

18 张林，吴普特，范兴科. 多点源滴灌条件下土壤水分运动的数值模拟[J].农业工程学报，2010,26(9):40-46.

ZHANG Lin, WU Pute, FAN Xingke. Numerical simulation of soil water movement with drip irrigation of multiple point source[J]. Transactions of the CSAE, 2010, 26(9): 40-46. (in Chinese)

19 SIMUNEK J, SE J M, VANGENUCHTEN M T.HYDRUS-2D simulating water flow,heat,and solute transport in two-dimensional variably saturated media[M].Calif: International Ground Water Modeling Center,Riverside,1999.

20 李久生,张群君,薛克宗.滴灌施肥灌溉原理与应用[M].北京:中国农业科学技术出版社,2003.

21 张效先.饱和条件下田间土壤纵向及横向弥散系数的试验和计算[J]．水利学报，1989,20(1):1-9.

ZHANG Xiaoxian.A method for determining the longitudinal dispersion parameters of field soils and lateral under saturated conditfion[J].Journal of Hydraulic Engineering,1989,20(1):1-9. (in Chinese)

22 马军花.农田土壤硝态氮运移动态的数学模拟[D].北京:中国农业大学, 2001.