啁啾相移光纤光栅分布式应变与应变点精确定位传感研究∗

裴丽 吴良英 王建帅 李晶 宁提纲

(北京交通大学光波技术研究所,全光网络与现代通信网教育部重点实验室,北京 100044)

1 引 言

精确定位传感技术在工业生产、安全防范、智能交通、科学技术以及国防建设等众多领域都有着重要而广泛的应用.随着我国现代化建设的飞速发展,设备的加工制造也逐渐朝着超大型化或微型化、精密化以及智能化的方向发展.开展应变与应变点精确定位传感技术的相关研究,对促进我国先进制造、精密加工、航空航天、铁路系统等高新技术行业的发展具有重要意义.

由于光纤光栅对温度、应变、环境折射率等都表现出了较高灵敏度的波长漂移或模场变化[1−6],光纤光栅被广泛应用于地震勘探[7]、海啸监测[8]、模型分析[9]以及结构检测等[10,11]领域.啁啾光纤光栅是一种周期不均匀的光纤光栅,其带宽比均匀光纤光栅的带宽更大,当在啁啾光纤光栅上的某一位置产生微应变时,该应变点会产生一个相移,啁啾光纤光栅的频谱则会出现一个与之对应的狭缝[12−14].狭缝的深度由应变量的大小决定,狭缝的中心波长由应变的位置和应变量共同决定.利用这一特性,啁啾光纤光栅可应用于应变与应变点的精确定位传感.当串接中心波长不同且通带范围互不重合的多个啁啾光纤光栅时,能够实现一定范围内的分布式应变与应变点精确定位检测,该精确定位传感装置可应用于先进制造、精密加工、航空航天、铁路系统等高新技术领域.

V-I传输矩阵法是一种可用于分析各种特殊光纤光栅的理论[15,16],本文利用V-I传输矩阵法建立狭缝深度和中心波长关于应变量和应变位置的理论模型,并通过实验论证啁啾相移光纤光栅对应变量的监测,以及对应变位置精确到微米量级的定位.实验中,用长度为100 m的普通单模光纤串接两个中心波长不同且通带范围互不重合的啁啾光纤光栅,实现分布式应变传感,实验获得的最大应变灵敏度为0.19 pm/µε.

2 理论模型及仿真分析

2.1 啁啾相移光纤光栅的 VV - III理论模型

当在啁啾光纤光栅上的某一位置处引入微应变时,即在该位置处引入一个相移,假设应变量的大小为s,引入的相移量为θ,则相移量θ与应变s的满足以下关系[12]:

其中,neff是啁啾光纤光栅的有效折射率,λz是啁啾光纤光栅上应变引入位置z处的布拉格波长.

则,该段啁啾相移光纤光栅的V-I传输矩阵表达式为

其中,V I1,V I2分别表示相移引入位置的前半段和后半段啁啾光纤光栅的V-I传输矩阵;A,B,C,D分别代表连乘矩阵的四个元素;Fθ表示由微应变形成的相移矩阵,可表示为

由此,得到啁啾相移光纤光栅透射率和反射率的表达式

其中,Z1,Z2分别对应每个光栅周期的前后半个周期的阻抗,且Z1≈neff+π/4,Z2≈neff−π/4.

由(1),(2),(3)和(4)式可知,啁啾相移光纤光栅的透射率或者反射率与引入相移的微应变s有着绝对的对应关系,我们可以根据检测到的啁啾相移光纤光栅频谱狭缝的透射率或者反射率得到应变量s.

啁啾相移光纤光栅频谱狭缝的中心波长是由应变位置和应变量共同决定的,则其中,λc是监测到的狭缝中心波长,λs是由应变s引起中心波长的漂移,且λz=2neffΛz,λs=2neffs,Λz是啁啾光纤光栅上应变引入位置z处对应的周期.则由(1)和(5)式可以推算得到

假设啁啾光纤光栅的周期呈线性分布,由(6)式可以精确定位应变位置z

其中,Λ0是线性啁啾光纤光栅初始端的周期,F是啁啾系数,L啁啾光纤光栅的长度.

由公式λz=2neffΛz可知,任意周期Λz和布拉格波长λz存在惟一的对应关系,即在微应变s已知的情况下,啁啾相移光纤光栅上任意周期Λz与狭缝的中心波长λc存在惟一的对应关系.由于啁啾光纤光栅上的周期分布是递减变化的,各处的周期大小均不相同,因此,理论上可以由狭缝的中心波长和深度计算出啁啾光纤光栅上产生微应变的位置相应的周期,从而实现精确到微米量级的定位.

图1 啁啾相移光纤光栅分布式应变与应变点精确定位传感的结构Fig.1.The structure of cascaded CFBGs applying in distributed strain and strain-points precise positioning.

2.2 啁啾相移光纤光栅分布式应变与应变点的精确定位传感结构

啁啾相移光纤光栅分布式应变与应变点精确定位传感结构如图1所示,将多个中心波长不同、通带范围互不重合的啁啾光纤光栅级联.已知,当两段光栅级联,级联光栅的频谱是两段光栅频谱的组合,与光栅之间的距离没有关系,且由于光栅色散的原因,光栅之间的距离仅对级联光栅的时延产生影响[17].当级联啁啾光纤光栅上的某一段或多段啁啾光纤光栅上的某一个或多个位置处引入微应变时,级联啁啾光纤光栅上产生对应的相移.通过对级联啁啾光纤光栅的频谱进行检测,当某一个透射峰出现狭缝时,粗定位产生微应变的啁啾光纤光栅,然后可以根据狭缝的深度和中心波长计算出应变量和应变产生位置处的周期,实现精确到微米量级的定位.

2.3 仿真分析级联啁啾相移光纤光栅

假设两段线性啁啾光纤光栅CFBG1和CFBG2,其中心波长分别为λ1=1544.58 nm,λ2=1548.60 nm,光栅长度L1=L2=3 cm,啁啾系数f1=f2=0.002,光纤有效折射率neff1=neff2=1.4513.将CFBG1和CFBG2级联,如图2(a)和图2(c)所示.由于CFBG1和CFBG2的频谱中心波长不同且通带范围互不重合,级联啁啾光纤光栅的频谱是啁啾光纤光栅CFBG1和CFBG2频谱的组合,如图2(b)和图2(d)所示.

图2 啁啾光纤光栅CFBG1和CFBG2级联 在CFBG1和CFBG2上各引入一个微应变的结构(a)及其频谱(b);在CFBG1上引入两个微应变的结构(c)及其频谱(d)Fig.2.Cascaded CFBG1 and CFBG2:the structure(a)and spectrum(b)of two CFBGs induced strain;the structure(c)and spectrum(d)of two strains induced in CFBG1.

我们之前的研究表明,当在啁啾光纤光栅上某一位置z处引入微应变s时,其透射谱的对应波长λz处会出现一个与之对应的狭缝,狭缝的深度随着应变量s的增加呈现先增加后减小的变化趋势,而狭缝的中心波长λc由应变的位置z和应变量s共同决定,所以λc随着应变量的增加向长波长漂移[14].同理,在如图2(a)所示的级联啁啾光纤光栅结构中,分别在CFBG1的中间位置z1,CFBG2的中间位置z2处引入微应变.令CFBG1和CFBG2在z1,z2处原本的周期分别为Λz1,Λz2,以及引入的应变量分别为s1,s2,则级联啁啾光纤光栅的频谱如图2(b)所示.由图2(b)可知,当在两个级联的光栅上分别引入微应变时,级联啁啾光纤光栅频谱的两个带宽范围内均出现了与啁啾光纤光栅上引入的微应变相互对应的狭缝,且狭缝的深度和中心波长的变化规律与单个啁啾光栅频谱中狭缝的深度和中心波长的变化规律一致.设置CFBG1上z1处的微应变s1为0.5µm,CFBG2上z2处的微应变分别为0.3µm,0.5µm和0.7µm,级联啁啾光栅的频谱中,微应变s1对应的狭缝几乎不变,微应变s2对应的狭缝的深度和中心波长按照前面所述的规律变化,由此证明,啁啾光纤光栅级联时,对于不同啁啾光纤光栅上的微应变,其频谱响应是相互独立的.

图2(c)中描述的是两个啁啾光纤光栅级联,在同一个啁啾光纤光栅上引入两个微应变的结构,其级联啁啾光栅频谱如图2(d)所示.从图2(d)可知,将两个啁啾光纤光栅级联,当在CFBG1上的z1,z2位置处引入微应变s1,s2,而CFBG2上未引入微应变时,级联啁啾光栅的频谱中,CFBG1带宽范围内出现两个与微应变s1和s2相互对应的狭缝,而CFBG2带宽范围内没有狭缝出现.CFBG1带宽范围内狭缝的深度和中心波长的变化规律与单个啁啾光纤光栅频谱中狭缝的深度和中心波长的变化规律一致.设置CFBG1上z1处的微应变s1为0.5µm,z2处的微应变分别为0.3µm,0.5µm和0.7µm,级联啁啾光栅的频谱中,微应变s1对应的狭缝几乎不变,微应变s2对应的狭缝的深度和中心波长的变化规律与前面所述的规律一致,由此证明,啁啾光纤光栅级联时,对于啁啾光纤光栅上的多个不同的微应变,其频谱响应是相互独立的.

上述理论分析表明,将啁啾光纤光栅级联,在不同的啁啾光纤光栅上引入微应变,或者在同一个啁啾光纤光栅上不同位置引入微应变,级联啁啾光栅频谱中均会出现与之相对应的狭缝,狭缝的深度和中心波长的变化规律一致,且每一个与微应变相对应的狭缝之间相互独立,该特性表明,级联啁啾光纤光栅可以应用于分布式应变与应变点精确定位传感.

3 实验与讨论

我们通过实验验证上述的级联啁啾光纤光栅在分布式应变与应变点精确定位传感的应用.将啁啾系数为0.024 nm/cm、长度为10 cm、中心波长为1544.675 nm、3-dB带宽为0.19 nm、透射深度约为10 dB的啁啾光纤光栅CFBG1和啁啾系数为0.024 nm/cm、长度为12.5 cm、中心波长为1546.605 nm、3-dB带宽为0.28 nm、透射深度约为14 dB的啁啾光纤光栅CFBG2级联,两段啁啾光纤光栅之间的单模光纤长度为100 m,利用两个相同的压电陶瓷片(Thorlabs,PK2FMP2,PZT)分别在两段啁啾光栅上引入微应变.采用的压电陶瓷片的最大应变量为11.2µm,尺寸为10.5 mm×6.1 mm×5.2 mm(长×宽×高).用紫外胶水将两个压电陶瓷片分别黏贴于两段啁啾光纤光栅的中间位置,即应变引入位置z1=5 cm,z2=6.25 cm,实验装置如图3所示.

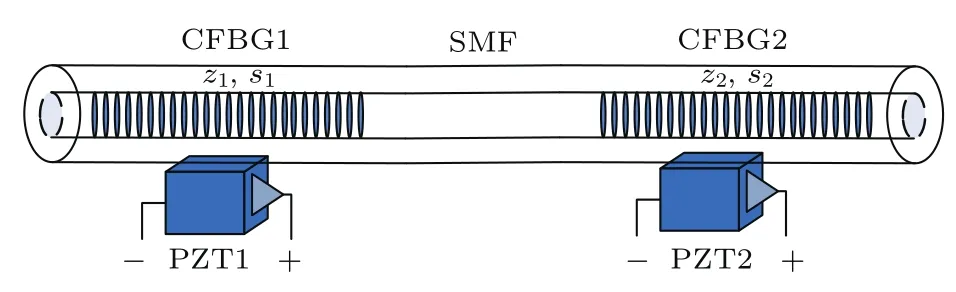
图3 啁啾光纤光栅CFBG1和CFBG2级联,且在CFBG1和CFBG2上均引入微应变的结构Fig.3.The structure of cascaded CFBG1 and CFBG2 with strains induced in both of CFBGs.

当在PZT1上加载驱动电压Vp1,而PZT2上未加载驱动电压时,利用光谱仪(YOKOGAWA,AQ6375)测得的级联啁啾光栅的频谱如图4(a)所示.图4(a)中CFBG1对应通带范围内的中心波长附近有狭缝产生,而CFBG2对应通带范围内没有狭缝.从图中可以看出,随着PZT1上驱动电压Vp1从5 V增加到75 V,CFBG1上引入的微应变逐渐增加,狭缝的中心波长逐渐从1544.664 nm漂移到1544.672 nm,并且狭缝的深度随着驱动电压Vp1的增加而增加,直到Vp1增加到60 V,狭缝深度到达最大值4.581 dB,CFBG1上狭缝的中心波长和深度随着驱动电压的变化曲线如图5(a)所示.

当在PZT2上加载驱动电压Vp2,而PZT1上未加载驱动电压时,测得的级联啁啾光栅的频谱如图4(b)所示.图4(b)中CFBG2对应通带范围内的中心波长附近有狭缝产生,而CFBG1对应通带范围内没有狭缝.从图中可以看出,随着PZT2上驱动电压Vp2从5 V增加到75 V,狭缝的中心波长逐渐从1546.568 nm漂移到1546.584 nm,深度从0.788 dB增加到9.065 dB,CFBG2上狭缝的中心波长和深度随着驱动电压的变化曲线如图5(b)所示.

图4 啁啾光纤光栅CFBG1和CFBG2级联频谱 (a)CFBG1上引入微应变;(b)CFBG2上引入为微应变;(c)CFBG1和CFBG2上同时引入惟一微应变Fig.4.Spectrum of cascaded CFBG1 and CFBG2:(a)strain in CFBG1;(b)strain in CFBG2;(c)strains in CFBG1 and CFBG2.

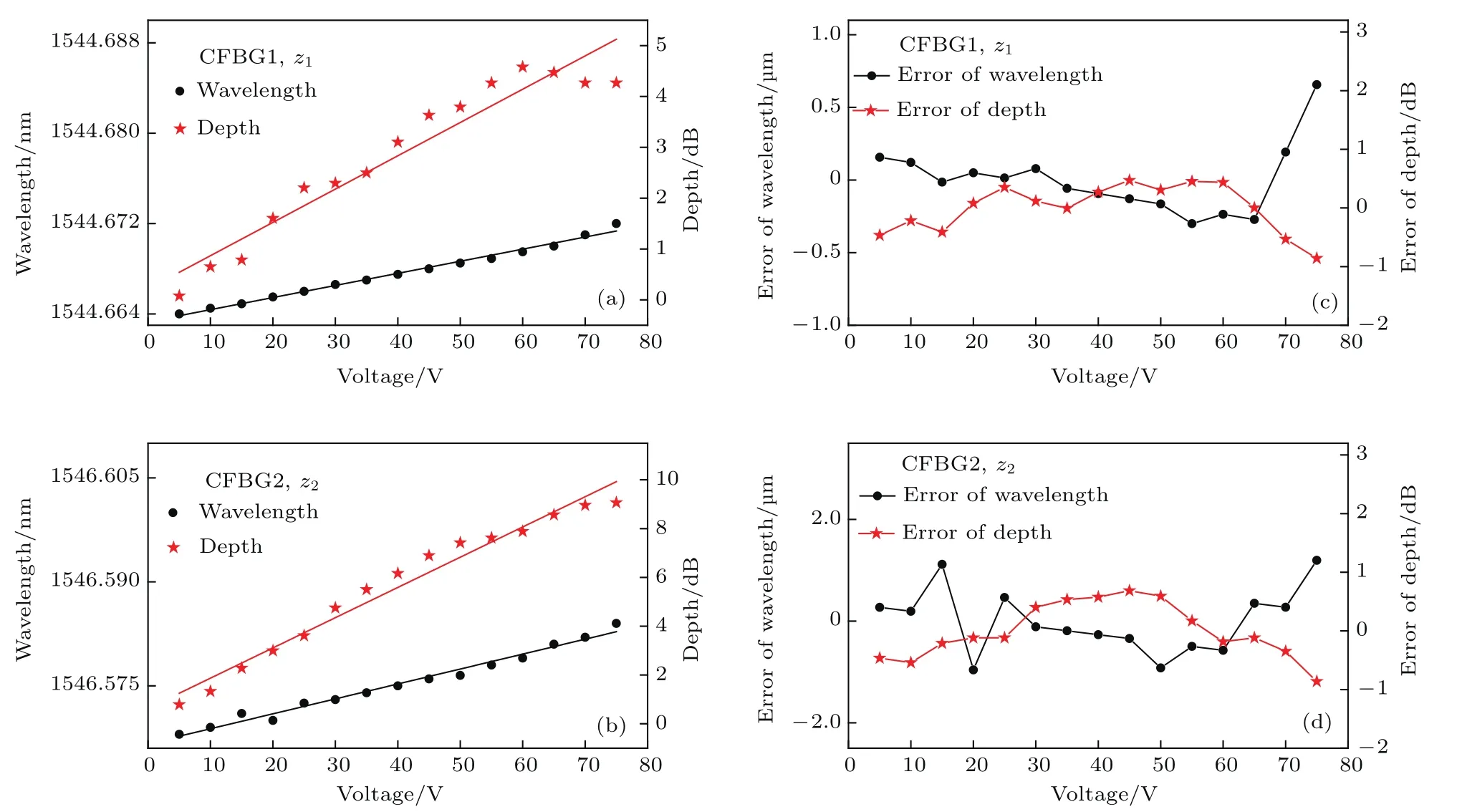
图5 驱动压电陶瓷片上的电压,CFBG1上狭缝的中心波长和深度(a)及其对应的误差(c),CFBG2上狭缝的中心波长和深度(b)及其对应的误差(d)Fig.5.Center wavelength and depth of peak(a)in CFBG1 and the error(c),center wavelength and depth(b)of peak in CFBG2 and the error(d),when the voltage applied on PZTs.

图4(c)是PZT1和PZT2上同时加载驱动电压时的级联啁啾光纤光栅的频谱,从该图可以看出CFBG1和CFBG2通带范围内均出现狭缝,且两个狭缝的中心波长和深度的变化规律,与图5所示的CFBG1和CFBG2上单独引入微应变时狭缝的中心波长和深度的变化规律一致.

对图5(a)和图5(b)中的实验数据进行拟合,发现CFBG1和CFBG2上的狭缝的中心波长和深度与驱动电压呈线性关系,且CFBG1上狭缝的中心波长和深度拟合曲线的斜率分别为0.0011 nm/V和0.0655 dB/V,CFBG2上狭缝的中心波长和深度拟合曲线的斜率分别为0.0022 nm/V和0.1239 dB/V.根据图5(a)和图5(b)计算CFBG1和CFBG2上狭缝的中心波长和深度的误差,如图5(c)和图5(d)所示,CFBG1上狭缝的中心波长和深度的最大绝对误差为6.57×10−4nm和0.85 dB,CFBG2上狭缝的中心波长和深度的最大绝对误差为1.2×10−3nm和0.86 dB.

假设压电陶瓷片PZT在电压的驱动下,通过拉伸产生的应变量与驱动电压的大小呈正比关系,根据图5(a)和图5(b)给出的CFBG1和CFBG2上狭缝中心波长随PZT上驱动电压的变化曲线以及PZT的最大拉伸量11.2µm进行计算,由此可以得出,CFBG1上引入微应变的应变灵敏度是0.08 pm/µε,CFBG2上引入微应变的应变灵敏度是0.19 pm/µε.

为了验证级联啁啾光栅,单个啁啾光栅引入多个微应变的情况,将啁啾系数为0.019 nm/cm、长度为12.5 cm、中心波长为1544.899 nm、3-dB带宽为0.34 nm、透射深度约为20 dB的啁啾光纤光栅CFBG1和啁啾系数为0.024 nm/cm、长度为12.5 cm、中心波长为1546.609 nm、3-dB带宽为0.28 nm、透射深度约为14 dB的啁啾光纤光栅CFBG2级联,两段啁啾光纤光栅之间的单模光纤长度为100 m,将PZT1和PZT2黏贴在CFBG1上z1=4.12 cm,z2=8.24 cm处,实验装置如图6所示.

该种情况下,级联啁啾光栅频谱中的狭缝变化规律与上述在级联啁啾光栅上均引入微应变时的变化规律几乎一致.当PZT1上加载驱动电压Vp3时,CFBG1对应通带范围内的短波长区有狭缝产生,测得的级联啁啾光栅的频谱如图7(a)所示,而当PZT2上加载驱动电压Vp4时,CFBG1对应通带范围内的长波长区有狭缝产生,测得的级联啁啾光栅的频谱如图7(b)所示.从图7(a)和图7(b)中可以看出,随着驱动电压Vp3和Vp4从5 V增加到75 V,z1位置对应狭缝的中心波长逐渐从1544.79 nm漂移到1544.804 nm,深度从0.131 dB增加到7.443 dB,而z2位置对应狭缝的中心波长逐渐从1545.012 nm漂移到1545.022 nm,深度从0.289 dB增加到9.068 dB,CFBG1上z1和z2位置对应狭缝的中心波长和深度随着驱动电压的变化曲线如图8所示.图7(c)是CFBG1上z1和z2位置同时引入微应变时的级联啁啾光纤光栅的频谱,从该图可以看出z1和z2位置同时引入微应变时,对应狭缝的中心波长和深度的变化规律与单独引入微应变时对应狭缝的中心波长和深度变化规律一致.

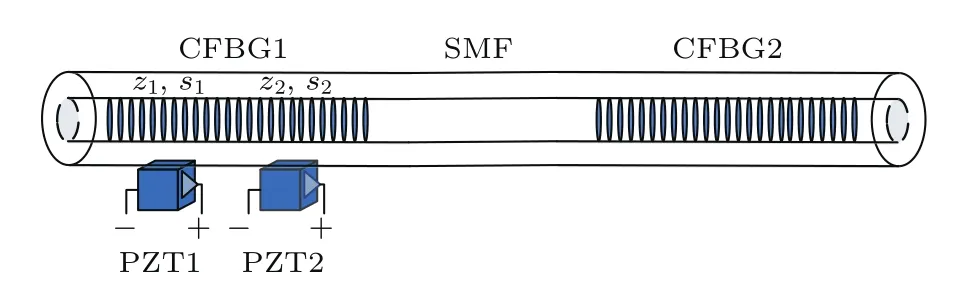
图6 啁啾光纤光栅CFBG1和CFBG2级联,且在CFBG1上引入两个微应变的结构Fig.6.The structure of cascaded CFBG1 and CFBG2,and two strains induced in CFBG1.

对图8(a)和图8(b)中的实验数据进行拟合,发现CFBG1上z1和z2位置处的狭缝的中心波长和深度与驱动电压呈线性关系,且CFBG1上z1位置狭缝的中心波长和深度拟合曲线的斜率分别为0.0002 nm/V和0.1028 dB/V,CFBG1上z2位置狭缝的中心波长和深度拟合曲线的斜率分别为0.0001 nm/V和0.1353 dB/V根据图8(a)和图8(b)计算CFBG1和CFBG2上狭缝的中心波长和深度的误差,如图8(c)和图8(d)所示,CFBG1上z1位置对应狭缝的中心波长和深度的最大绝对误差为1.46×10−3nm和1.18 dB,CFBG1上z2位置对应狭缝的中心波长和深度的最大绝对误差为1.36×10−3nm和1.02 dB.

图7 啁啾光纤光栅CFBG1和CFBG2级联频谱 (a)CFBG1上z1位置引入微应变;(b)CFBG1上z2位置引入为微应变;(c)CFBG1上z1和z2位置同时引入惟一微应变Fig.7.Spectrum of cascaded CFBG1 and CFBG2:(a)Strain in z1of CFBG1;(b)strain in z2of CFBG1;(c)strains in z1and z2of CFBG1.

图8 驱动压电陶瓷片上的电压,CFBG1上z1位置对应狭缝的中心波长和深度(a)及其对应的误差(c);CFBG1上z2位置对应狭缝的中心波长和深度(b)及其对应的误差(d)Fig.8.Center wavelength and depth of peak(a)at position of z1of CFBG1 and the error(c);center wavelength and depth of peak(b)at position of z2of CFBG1 and the error(d),when the voltage applied on PZTs.

根据图8(a)和图8(b)给出的狭缝中心波长随驱动电压的变化曲线换算,CFBG1上z1位置处引入微应变的应变灵敏度为0.17 pm/µε,CFBG1上z2位置处引入微应变的应变灵敏度为0.12 pm/µε.将此种情况下的得到的应变灵敏度和上述两个压电陶瓷片分别黏贴与两个啁啾上光栅得到的应变灵敏度进行比较,发现同样的压电陶瓷片和驱动电压下,应变灵敏度存在差异,而造成这种差异的原因如下:一是在实验过程中由于手动误差,PZT并不是全部黏贴在啁啾光纤光栅上,二是PZT的拉伸应变量与驱动电压并不是绝对的线性关系.

4 结 论

本文通过理论和实验验证,啁啾光纤光栅级联时,不同啁啾光纤光栅上的微应变之间以及同一个啁啾光栅上的不同微应变之间都是相互独立的,且在级联啁啾光纤光栅上的任意位置处引入为微应变,级联啁啾光栅频谱中均会出现与之对应的狭缝.狭缝的深度由应变量的大小决定,狭缝的中心波长由应变的位置和应变量共同决定.因此,可以将级联啁啾光纤光栅应用于分布式应变与应变点定位,当在级联啁啾光栅频谱中观察到狭缝时,首先可以粗定位产生微应变的某段啁啾光纤光栅,然后根据狭缝的深度计算应变量的大小,并根据狭缝的深度和中心波长对微应变产生的位置,进行精确到微米量级的定位.实验成功验证了级联啁啾光纤光栅在分布式应变传感上的应用,获得的最大灵敏度为0.19 pm/µε.

[1]Morey W W,Meltz G,Glenn W H 1989Proc.SPIE116998

[2]Patrick H J,Williams G M,Kersey A D,Pedrazzani J R,Vengsarkar A M 1996IEEE Photon.Tech.L.81223

[3]Liang W,Huang Y,Xu Y,Lee R K,Yariv A 2005Appl.Phys.Lett.86151122

[4]Guan B O,Tam H Y,Tao X M,Dong X Y 2000IEEE Photon.Tech.L.12675

[5]Cai Z,Liu F,Guo T,Guan B O,Peng G D,Albert J 2015Opt.Express2320971

[6]Chryssis A N,Lee S M,Lee S B,Saini S S,Dagenais M 2005IEEE Photon.Tech.L.171253

[7]Laudati A,Mennella F,Esposito M,Cusano A,Giordano M,Breglio G,Sorge S,Calisti T C,Torre A,D’Altrui G,Cutolo A 2007Proc.SPIE661966191C

[8]Fujihashi K,Aoki T,Okutsu M,Arai K,Komori T,Fujita H,Kurosawa Y,Fujinawa Y,Sasaki K 2007Symposium on Underwater Technology and Workshop on Scienti fic Use of Submarine Cables and Related Technologies IEEE349

[9]Capoluongo P,Ambrosino C,Campopiano S,Cutolo A,Giordano M,Bovio I,Lecce L,Cusano A 2007Sensor Actuat.A:Phys.133415

[10]Chan T H T,Yu L,Tam H Y,Ni Y Q,Liu S Y,Chung W H,Cheng L K 2006Eng.Struct.28648

[11]Schulz W L,Conte J P,Udd E 2001Proc.SPIE433056

[12]Chen X,Painchaud Y,Ogusu K,Li H 2010J.Lightwave Technol.282017

[13]Xian L,Li H 2013J.Lightwave Technol.311185

[14]Wu L Y,Pei L,Liu L,Wang J S 2016Opt.Laser Technol.7915

[15]Capmany J,Muriel M A,Sales S,Rubio J J,Pastor D 2003J.Lightwave Technol.213125

[16]Victor G M,Muriel M A,Capmany J 2005IEEE Photon.Tech.L.172343

[17]Ning T G,Fu Y J,Tan Z W,Liu Y,Pei L,Jian S S 2004Chin.J.Lasers3177(in Chinese)[宁提纲,傅永军,谭中伟,刘艳,裴丽,简水生2004中国激光3177]