中国林业技术效率与全要素生产率增长分解*——基于SFA-Malmquist方法的估计

史常亮 揭昌亮 石 峰 温亚利

(1.中国农业大学经济管理学院 北京100083； 2.江西省社会科学院城市经济所 南昌330077； 3.北京林业大学经济管理学院 北京100083)

林业的快速、稳定发展，对实现社会、经济、生态的全面可持续发展具有重要意义。以2003年国家集体林权制度改革实施为标志，我国林业发展进入了一个继家庭联产承包责任制之后农村经营制度又一重大变革的新时期。在政策、市场、改革的合力推动下， 2001—2014年全国林业总产值连续14年保持了年均22%的高增长。最新统计数据显示， 2016年，我国林业产业总产值已达到6.49万亿元，比2015年增长9.3%，远高于同期国民经济6.7%的增长率。然而，在林业产业规模不断扩大的同时，我国林业发展中存在的一些资源不足、效率不高、经营粗放、机制不顺等问题也逐渐暴露出来； 特别是近年来，由各国生态环境保护力度增强导致的国际林产品及木材市场供需压力的持续上升，使我国林业发展面临前所未有的挑战。如何推动实现林业发展方式由粗放型向集约型转变，已成为当前我国林业发展过程中亟待解决的问题。

转变林业发展方式，就是由过去主要依靠资本、劳动力等投入要素的增加转变到主要依靠提高生产要素的使用效率上来，即要提高全要素生产率(total factor productivity，TFP)在林业经济增长中的贡献份额(魏远竹等， 2001)，因此，如何准确测算林业TFP显得格外重要。在国外，这方面研究主要沿着2个方向展开： 一是针对具体国家或地区，分析其林业TFP变动情况(Managi， 2010； Korkmaz， 2011； Zangetal.， 2015)； 二是分析某一具体林业行业的TFP变动情况(Hseuetal.， 2005； Zhangetal.， 2006； Helvoigtetal.， 2009)。在这些研究中，生产函数法、增长核算指数法、基于数据包络分析(data envelopment analysis，DEA)的Malmquist或Luenberger生产率指数法以及随机前沿分析(stochastic frontier approach，SFA)都得到了广泛应用。

与国外相比，我国对林业TFP的测算研究起步较晚，但发展迅速。马天乐等(1992)较早运用增长核算指数法对全国1956—1985年的林业TFP进行测算，结果发现，期间我国林业总产出增长基本上被林业要素投入增长所占据，TFP的贡献率低而不稳。陈晓兰等(2014)、徐玮等(2015)、黄安胜等(2015)分别使用省级面板数据和DEA-Malmquist指数法测算了1995—2011年、1998—2012年和2004—2012年的林业TFP增长率，初步形成了一些具有共识性的结论： 我国林业TFP增长主要依靠技术进步推动，技术效率改善在其中的作用十分有限。还有一些学者使用地区层面的面板数据，如刘清泉等(2014)对广东省、周子桥等(2015)对黑龙江省、刘璨等(2006)对东北国有林区、陈向华等(2012)对黑龙江国有林区、李京华等(2016)对内蒙古国有林区的研究，也得到了类似结论。

总体而言，目前国内有关林业TFP的测算成果是丰富的。但也应该看到，虽然已有研究初步认识到技术效率改善不足是造成中国不同省份林业TFP增长差异的原因所在，但究竟是哪些因素造成了这种差异以及如何改进，现有研究却缺乏深入探讨。从方法论的角度看，现有文献对于中国林业TFP的测算基本都建立在DEA基础上，该方法的一大缺陷是没有考虑环境因素和随机误差对效率评价的影响，且对于样本数据中的异常值相当敏感。而林业无疑是一个充满噪声的行业，受自然气候、国家宏观政策的影响程度大，异常值难免不会出现。在这种情况下，SFA方法作为一种替代，尽管存在需要先验设定前沿生产函数和随机项的概率分布等缺陷，但正是因为对随机误差和效率损失进行了分离处理才使得被估计的效率值更贴近实际； 富有弹性的超越对数生产函数设定，也能够较好地避免由于生产函数形式误设带来的估计偏差(傅晓霞等， 2007； 史常亮等， 2016)。因此，对于林业生产而言，基于SFA方法得出的结论应该更可靠。

另外一个重要问题是，现有文献对于林业TFP增长的分解全都沿用了Färe等(1994)的框架，即假设技术规模报酬可变(VRS)，进而将TFP增长分解为技术效率变化、技术变化和规模效率变化3部分。但是，正如Grifell-Tatjé等(1995)指出，由于该分解方法对于技术变化的测算是基于虚拟的规模报酬不变(CRS)前沿面而不是实际的VRS前沿面，通常会产生一个向上偏误的技术变化值和向下偏误的规模效率变化值； 也就是说，当假设VRS技术时，该方法并不能正确测算TFP的变化情况。Ray等(1997)确认了这种分解的不一致性。因此，从这个角度讲，现有文献直接按照Färe等(1994)的思路对中国林业TFP进行分解和测算，所得结果很可能是存在偏差的。

有鉴于上述情况，本文拟在以下3方面对现有文献进行拓展： 1) 运用Malmquist生产率指数与SFA模型相结合的方法，对中国2004—2015年的林业TFP增长率进行再测算，通过对所估计的生产技术施加CRS约束1)，避免了TFP分解的有偏问题； 2) 利用SFA“一步法”模型将外部环境的变化因素同时带入到对林业技术效率的估计中，提高了估计结果的有效性，并方便找出造成省份间林业技术效率差异的原因； 3) 从时间和空间2个角度对10多年来中国林业TFP增长的动态趋势与省际差异进行分析，并将TFP分解为前沿技术变化和技术效率变化2部分，以确认不同省份林业TFP增长的来源。

1) 正如科埃利等(2008)所指出，在施加CRS技术的情况下，规模效率或不存在或能够被吸纳入技术效率变化当中； 而如果不施加CRS技术，则需要把规模效率对TFP的影响估计出来，否则所得到的测算结果将不能正确反映由规模效应引起的TFP的增减情况。

1 研究方法、变量与数据

1.1 研究方法

在TFP增长率的分解中，技术效率的估计极为关键。本文采用Battese等(1995)提出的SFA“一步法”模型对中国林业技术效率进行测算，其最大特点是可同时对前沿生产函数和技术无效率方程进行估计，避免了传统“两步法”造成的估计不一致问题(Wangetal.， 2002)。目前，该模型已经推广到面板数据的分析中，其一般形式为：

lnYit=lnf(Xit,T;β)+(vit-μit)。

(1)

式中： 下标i和t分别表示省份和时间；Yit为总产出；Xit为一组投入要素向量；T为时间趋势项，用于解释技术变迁；β代表所有待估计系数；f(·)为前沿生产函数，表示经济中最优生产技术，其可以选择不同的函数形式，比较常用的有C-D生产函数和超越对数生产函数。

为降低函数形式误设的风险，这里采用形式相对灵活、包容性强的超越对数函数：

(2)

式中：Yit表示省份i在t时期的实际林业产出；Xnit表示第n个投入变量，在本文中分别为资本(K)、劳动力(L)和土地(S)；Dj为地区虚拟变量，用以控制那些观测不到的、不随时间变化的地区特征对回归结果的影响，j=1、2、3、4分别表示该省份属于东北、东部、中部和西部地区。

为满足CRS假设，并符合超越对数函数的对称性特征，对式(2)中的投入与产出使用土地投入S进行标准化，使其转化为针对土地的密集形式：

lnyit=β0+β1lnkit+β2lnlit+β3T+

β4(lnkit)2+β5(lnlit)2+β6T2+β7lnk×

lnl+β8T×lnk+β9T×lnl+αjDj+νit-μit。

(3)

式中：yit=Yit/Sit表示省份i在t时期的地均林业产出；kit=Kit/Sit表示地均资本投入；lit=Lit/Sit表示地均劳动力投入；β、α为待估计参数；vit为传统的随机误差项，用于控制统计噪音，假定服从对称的正态分布，即vit～N(0,σv2)；uit为非负的技术无效率项，独立于vit，假定服从如下形式的断尾正态分布：

(4)

式中：mit对应的函数即为技术无效率函数；Zit为一组特定环境变量，用以解释技术效率变化；δ为对应的待估计参数向量，其符号与影响效应相反；T、D的含义同上，其中系数η反映技术效率变化的时间特征，符号为正代表技术效率是递减的，反之亦然；φj度量了东部、中部和西部虚拟变量(以东北为参照组)对技术无效率程度的影响系数；ωit为该回归方程的随机误差项，服从对称的正态分布，即ωit～N(0,σw2)。

对于式(3)、(4)确定的面板SFA模型，可以通过联立的极大似然法(MLE)一步估计得到模型的所有参数。从而，省份i在t时期的林业技术效率TEit可通过下式估计获得：

TEit=exp(-uit)。

(5)

测算出林业技术效率后，结合Malmquist生产率指数就可以进一步测算省份i在t时期和t+1时期之间的林业TFP变化，其被定义为技术效率变化指数与前沿技术变化指数的乘积(Färeetal.， 1994)，即：

(6)

式(6)右边的第1项TECHit,t+1即为技术效率变化指数，刻画了既定技术条件和要素投入下生产单元对生产前沿面的逼近或远离对其TFP变化的影响，其数值可通过下式计算得出：

(7)

式(6)右边的第2项TPCHit,t+1即为前沿技术变化指数，刻画了既定要素投入下生产前沿面的外移或内陷对生产单元TFP变化的影响，其数值可通过生产函数对时间T求偏导数得出。根据Coelli等(2000)、Fuentes等(2001)的研究，当技术变化非中性时，技术变化速度受投入向量的影响，因此相邻时期的技术变化应取几何平均值，即：

(8)

1.2 变量选取

1.2.1 产出指标 本文选取林业总产值(亿元)作为产出(Y)的衡量指标。林业总产值囊括了林业三次产业产值，是现行统计资料中较为系统、全面和可靠的一套产出指标。为了保证跨期样本资料的可比性，利用官方公布的林产品生产价格指数(个别省份少数年份数值缺失，用全国同期指数代替)进行2004年不变价处理。

1.2.2 投入指标 投入主要包括资本(K)、土地(S)和劳动力(L)3个方面。其中，资本数据根据各省林业固定资产投资完成额(亿元)采用永续盘存法推算，基本公式为：Kit=(Iit/Pit)(1-δi)Ki,t-1[式中：Kit为省份i在第t年的林业资本存量；Iit为省份i在第t年的林业固定资产投资完成额；Pit为2004年不变价固定资产投资价格指数(2004年为1)；δi为各省资本折旧率，取值来自吴延瑞(2008)]。为计算Kit，还需确定基期(即2004年)的资本存量Ki,0。借鉴宋长鸣等(2012)的做法，本文以各省2004年的林业固定资产投资完成额除以10%作为基期资本存量。

对于土地和劳动力投入，与已有文献的普遍处理相同，分别选用森林面积(万hm2)和林业系统年末从业人员(万人)来衡量。

1.2.3 林业技术效率影响因素 在实际生产活动中，有一些外部变量虽然并不直接进入生产(既不是生产过程中的投入，也不是产出)，但却会影响生产者行为，进而影响决定投入转化为产出的技术结构或效率。在估计技术效率时，将这些外部变量融入到效率测度模型中，将有助于得到更有效的估计结果。根据已有研究，本文定义式(4)中林业技术无效率项的外生解释变量Zit包括：

将车子泊在停车场，念蓉走进酒店大堂。她弄不清自己到底想干什么，她只知道此时，两条腿似乎完全不再属于自己。电梯在十二层停下，念蓉走出去，脚踩上厚厚的地毯，两腿软得抬不起来。她记得房卡上的号码——1 2 1 0，那代表着一个封闭并且私密的空间：厚厚的窗帘，舒适的大床，飘着玫瑰花瓣的洗澡水，两个纠缠在一起的身体……

1) 年降水量(rain) 林业生产的对象是有机生物，光、水、热等气候因素在其中的重要性不容忽视。Lee(2008)、田杰等(2013； 2015)详细讨论了加入气温、降水量等气候因素对于林业技术效率评价的必要性。本文对林业技术效率的估计亦考虑了气候因素，但在具体做法上，一方面，考虑到与劳动、资本、土地不同，这些因素不是生产要素，不宜直接放入前沿生产函数，但其会影响生产要素的使用效率进而影响总产出，因此适宜作为外生变量引入无效率方程； 另一方面，考虑到如果同时纳入4—10月平均气温和降水量2个变量，会导致严重的多重共线性(Pearson相关系数达到0.722)，因此为简化模型，只考虑了降水量指标。与田杰等(2013； 2015)的做法类似，本文以各省会城市(或直辖市)的全年降水量(mm)作为各省年降水量的代表。

2) 森林火灾受害面积(fda) 森林火灾是影响林业稳定健康发展的另一种主要灾害，也是中国森林资源面临的最主要风险源。臧良震等(2014)对西部地区的研究发现，森林火灾受害面积对该地区不同阶段的林业技术效率均有显著影响。借鉴其研究，本文将森林火灾受害面积(万hm2)作为一个重要的环境变量纳入无效率方程。

3) 森林病虫鼠害发生面积(opra) 病虫鼠害被喻为“不冒烟”的森林火灾，其传播和蔓延对林木生长具有不可估量的损害作用。宋长鸣等(2012)研究发现，病虫鼠害对林业技术效率造成了显著的负面影响，是目前效率损失的重要原因。基于此，本文选取森林病虫鼠害发生面积(万hm2)作为重要的环境变量引入模型。

4) 森林病虫鼠害防治面积(cpra) 鉴于病虫鼠害对森林的巨大危害，其有效防治对于促进整个林业的健康发展无疑至关重要。根据田杰等(2013)的研究，本文亦将森林病虫鼠害防治面积(万hm2)作为影响林业技术效率的重要变量嵌入无效率方程。

5) 林业专业技术人员数(pt) 在给定生产技术及外部环境的情况下，提高农户技术效率的手段不外乎教育和培训2种。李谷成等(2008)认为，相较于劳动力的受教育程度，专门的技术培训对于提高农户技术效率具有更为显著的作用。在我国，各级林业工作站专业技术人员是实施林业技术培训的主体。一般来说，平均到每个省份的林业技术人员数越多，当地农民获得更多林业技术培训的可能性就越大。因此，本文以各省拥有的林业专业技术人员数(千人)来反映农户受到的技术培训状况。

最后，考虑到不同区域在资源禀赋、经济发展、气候条件、地理等方面存在较大差异，本文还在模型中引入了东部、中部和西部(以东北为参照组)3个虚拟变量来区分4大区域之间不可观测因素对林业产出和林业技术效率的可能影响。东部地区包括河北、天津、北京、山东、江苏、上海、浙江、福建、广东和海南10省， 中部地区包括山西、安徽、江西、湖北、湖南和河南6省， 西部地区包括四川、重庆、内蒙古、贵州、云南、陕西、广西、甘肃、新疆、青海和宁夏11省， 东北地区包括黑龙江、吉林和辽宁3省。

1.3 数据来源

由于研究所涉及的部分指标数据在2004年之前缺失严重，因此本文所用样本为2004—2015年； 研究对象为中国大陆地区30个省、市、自治区(西藏自治区由于数据残缺不全而予以舍弃)。用于分析的基础数据主要来自《中国林业统计年鉴(2004—2015)》和国家统计局数据库，个别省份少量缺失数据利用线性趋势法或内插法加以填补。

2 实证分析结果

2.1 面板SFA模型估计结果

对面板SFA模型的最大批评是其结论高度依赖于模型的函数形式。为避免由于函数形式误设造成的可能偏误，本文从形式最为一般的超越对数生产函数出发，利用广义似然比(LR)检验1)，从设定的待估计模型中筛选出最好拟合了样本数据的模型。检验结果见表1。其中，假设1认为前沿生产函数采用C-D函数形式更合适； 假设2和3则分别假定在样本期内不存在技术变化以及技术变化相对于投入呈希克斯中性； 假设4认为在无效率方程中不应纳入时间趋势项，即假设技术效率不随时间变化； 假设5认为在无效率方程中不应存在地区虚拟变量； 假设6则进一步认为应从无效率方程中剔除包括时间趋势项和地区虚拟变量在内的所有外部环境变量。

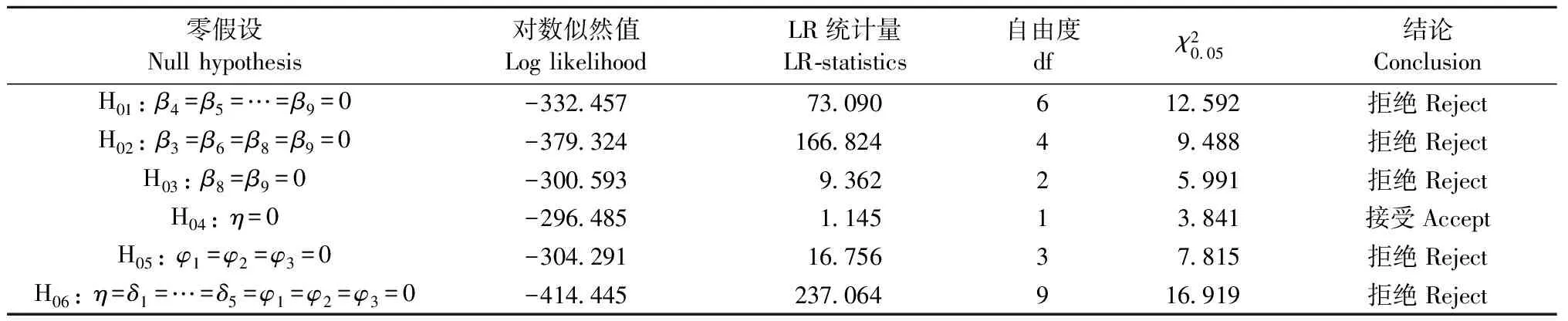
表1 模型设定检验结果Tab.1 Likelihood ratio tests for alternative model specifications

2) 基准模型的对数似然函数值为-295.913 。

通过计算LR统计量发现，相对于式(3)、(4)定义的基准模型2)，假设1～3及假设5和6均被拒绝； 而假设4在5%显著性水平上没有被拒绝。这表明，假设4对应的模型最好地拟合了样本数据，因此本文将其作为测度林业技术效率的主要模型。估计结果如表2所示，绝大多数变量都高度显著，证明模型拟合较好； 误差项方差中技术无效率方差所占比重γ为0.933，且在1%水平上显著，说明实际产出偏离前沿产出主要是由技术无效率而非白噪声所引起，本文中SFA模型的设定得到了检验的支持。

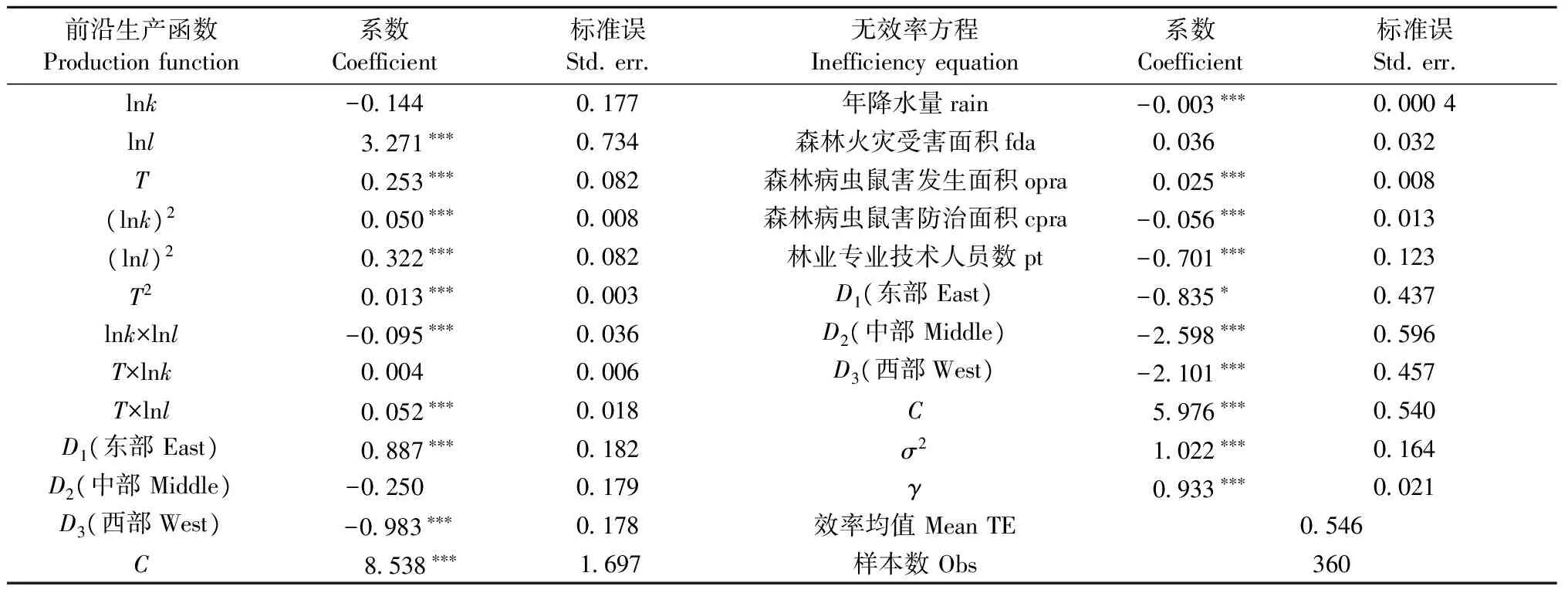
表2 随机前沿模型的极大似然估计结果①Tab.2 Maximum likelihood estimates for the parameters of SFA model

①***、**、*分别表示在1%、5%、10%的显著性水平上显著。***, ** and * represent the significance in the level of 1%, 5% and 10% respectively.

得到模型参数后，结合式(5)即可计算出2004—2015年中国林业技术效率，平均为0.546，远小于1，表明中国林业生产中存在着比较普遍的技术无效率现象，远未发挥出已有投入经费和从业人员的全部潜力； 但反过来也说明其提升空间很大。与以往文献相比，本文测算结果要小于田淑英等(2012)使用DEA得到的结果0.994。究其原因，除了投入产出指标选取不同及样本区间差异外，还可能与本文采用的SFA方法充分考虑了随机误差因素对前沿面的影响有关。作为一种特殊的自然产业，林业生产是“经济再生产与自然再生产的结合”，生产中存在着诸多不可控因素(如气候、火灾等)。而DEA忽略了这些随机因素的影响，所有偏离前沿面的因素都被假定为来自于技术无效，随机误差的影响被包含到效率项的估计中；特别是当随机误差项占总体方差的比重较大时，DEA测算的结果偏差会很严重(Bergeretal.， 1997)。在本文中，误差项占比接近10%(1～0.933)，因此，利用SFA方法得出的结论应该与真实情况更逼近。

表2中右半部分的无效率方程给出了各环境变量对林业技术效率变化的影响。其中，年降水量的系数估计值为负，且通过了1%水平的显著性检验，表明降水对林业技术效率有明显的提升作用，符合林业生产主要依赖气候条件的认知。森林病虫鼠害防治面积、林业专业技术人员数也通过了1%水平的显著性检验，且估计系数均为负，表明这2项因素的提升能有效改进林业生产中的技术效率。森林病虫鼠害发生面积的估计系数为正，且在1%水平上显著，说明森林病虫鼠害发生对林业技术效率具有显著的负面影响。森林火灾受害面积虽然没有通过显著性检验，但其估计系数为正，说明该灾害的发生在某种程度上也会造成林业技术效率损失。区域虚拟变量(Dj)中，东部、中部和西部的系数估计值均为负，且均通过了相应水平的显著性检验，意味着这3个地区的林业技术效率水平要比东北地区高。

2.2 中国林业TFP增长率测算结果分析

根据以上结果，利用式(6)～(8)即可计算出各省2004—2015年的技术效率变化、前沿技术变化和TFP变化的Malmquist指数。表3给出了以各省几何平均计算的全国林业TFP变化的Malmquist指数。数据显示，样本期内中国林业TFP经历了程度相当可观的增长，年均增长16.48%，略高于黄安胜等(2015)使用DEA-Malmquist指数法得到的估计结果15.6%，符合SFA得到的TFP-Malmquist指数要高于DEA结果的一般经验(傅晓霞等， 2007)。从TFP成分看，与已有文献一致，研究期间中国林业TFP增长主要源于生产前沿的移动，即技术进步。2004—2015年，整体林业技术变化指数年均增长16.92%，构成林业TFP增长的主要动力源泉； 而林业技术效率在绝大对数年份呈恶化状态，年均下降0.37%，在一定程度上弱化乃至抵消了前沿技术进步对TFP增长所做的贡献。

从TFP的角度，由技术进步主导还是效率改善主导有着不同的政策含义： 前者表示一个国家或地区对新技术的局部创新，后者则强调生产单元对现有技术的消化、吸收和利用程度。我国林业TFP增长呈现出前沿技术进步与技术效率损失并存的现象表明， 过去10多年里，我国林业科研体系虽然在技术创新与发明方面取得了相对成功，极大带动了林业产业的增长； 但整个林业推广体系在对现有技术的消化利用和扩散推广上却并不理想，当前偏低的林业技术效率水平佐证了这一点。

表3 2004—2015年中国林业全要素生产率增长率及其分解①Tab.3 China forestry total factor productivity indexand its components during 2004—2015

①各指数均为历年各省份的几何平均数，最后一行所列平均值亦为各年份的几何平均数； 表中各指数减去1，即为相应各指标的增长率。All Malmquist index averages in table are geometric means. Every Malmquist index in table minus 1 is its growth rate.

2.3 中国林业TFP增长的时间特征分析

1) 即2004年的TFP为1， 2005年的TFP等于2004年的TFP乘以2005年的Malmquist生产率指数，依此类推。

Malmquist指数测算的TFP是本年相对于上年的变化率。为了能够反映长时期的演变趋势，可以将其转换成以2004年为基期的累积变化率形式1)，如图1所示。样本期内，中国林业技术变化与技术效率变化存在着显著差异： 前者表现为明显波动增大特征，后者则呈现出缓慢的波动减小趋势，并且每当前者有力地推动TFP增长时，总会遇到后者下降对TFP增长的不利影响，而很少见到二者同时增长的情况。这种技术进步与技术效率改善相背离的TFP增长模式，也出现在中国农业生产中(史常亮等， 2016)。

从时间趋势上分析，中国林业TFP在2004—2010年增长减缓，一直到2011年才开始出现小幅增加。特别是2007—2010年，受低温雨雪冰冻自然灾害和国际金融危机的严重影响，林业生产遭受重大打击，林业技术效率出现大幅下滑，极大抵消了林业技术进步对TFP增长的贡献，导致 TFP连续3年衰退。为了尽快恢复自然灾害破坏的林业基础设施，同时也为了应对金融危机的挑战，2010年开始，国家连续几年数次追加中央林业投资，其中仅2011年中央林业投资就达到1 220.3亿元，比2010年增加260多亿元，这对林业TFP的止步回升起到了明显作用。2011—2012年，全国林业TFP同比增长26.78%，比以往任何时间都增长迅猛； 但是，急剧增加的林业投资也给林业技术效率提升带来了负面影响。由于组织管理能力没有及时跟上投资规模的扩大，一些地方甚至出现了突击完成投资任务的现象，导致林业投入产出规模和结构偏离最优水平，效率损失严重(田淑英等， 2012； 田杰等， 2013)。体现在数据上就是， 2013—2015年虽然林业技术进步指数逐年提高，但林业技术效率却处于恶化之中，从而大大妨碍了林业TFP获得更快增长。从图1中也可以看到， 2012年以来，林业技术效率指数一直都处于递减趋势，相应的林业TFP的增长速度亦呈现出震荡略有下降趋势。

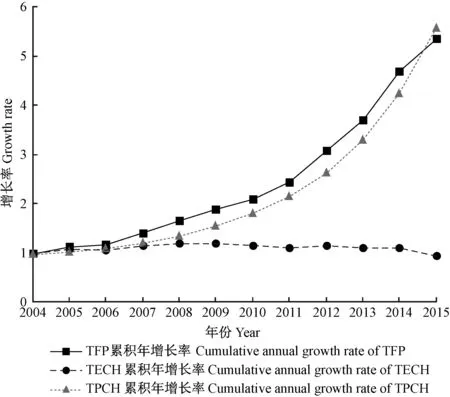
图1 林业技术效率指数、技术进步指数和TFP累积年增长率Fig.1 The cumulative annual growth rate of TPCH, TECH and TFP

2.4 中国林业TFP增长的空间特征分析

表4给出了以历年几何平均计算的各省份、各区域林业TFP变化的Malmquist指数。分省份来看，样本期内，除北京外几乎所有省份都实现了林业TFP正增长。其中，以上海表现最为优异，TFP增长最快，年均达到42.92%，并且提高TFP的来源比较均衡，林业经济增长可持续较强；与之相反，北京的林业TFP增长情况则比较糟糕，出现了负增长，年均增长-6.15%，技术效率恶化是造成其林业TFP负增长的主要原因。2004—2015年，北京市林业技术进步年均增长27.68%，远高于同期全国16.92%的平均增长速度； 但林业技术效率却以年均递减26.50%的速度处于不断恶化之中，是30个样本省份中表现最糟糕的省份，技术效率的年均负增长完全抵消了技术进步的增长，林业增效任务最为艰巨。

在29个实现林业TFP正增长的省份中，有15个省份表现为“双驱动”型增长模式，分别为天津、辽宁、上海、浙江、安徽、福建、江西、河南、广东、海南、四川、贵州、陕西、青海和新疆，其共同特点是在保持林业前沿技术快速进步的同时，林业技术效率也得到了有效提升。其余14个省份则表现为林业技术进步与林业技术效率损失并存的“单驱动”型增长模式，其特点是虽然技术变化指数增长明显，但由于存在技术的“适宜性”问题，技术效率处于恶化状态。在这些省份中，尤为值得一提的是江苏、甘肃、山西、吉林和黑龙江等省份，其虽然在技术进步方面表现得颇为优异，增长速度远远高于同期其他省份，但由于对现有技术的有效利用跟不上生产可能性边界向外扩张的速度，导致林业技术效率恶化严重，极大阻碍了林业TFP获得更快增长。

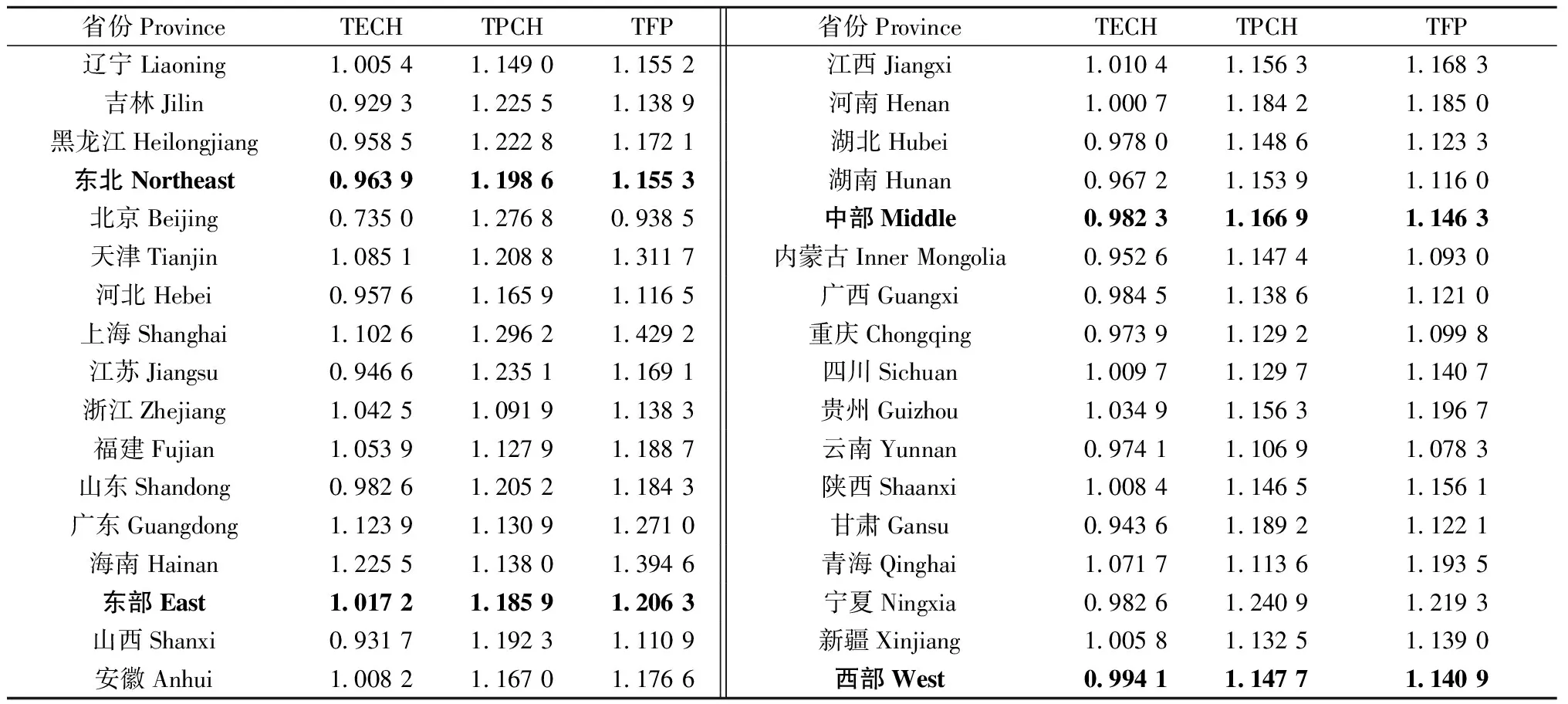
表4 各省份、区域林业TFP增长及其分解①Tab.4 The growth rate of TFP in each province and regions and its decomposition

① 各指数均为各省份历年的几何平均数，各区域平均值亦为区域内相应省份历年的几何平均数； 表中各指数减去1，即为相应各指标的增长率。 All Malmquist index averages in table are geometric means. Every Malmquist index in table minus 1 is its growth rate.

分区域来看，4大区域中，东部地区的林业TFP增长最快，年均增长20.63%，超出全国平均水平4.15个百分点； 东北地区次之，年均增长15.53%，略低于全国平均增速0.95个百分点； 中部和西部地区的林业TFP增长不相上下，但都低于全国平均水平，分别为14.63%和14.09%。在TFP增长的内部构成上，与全国一样，技术进步始终是推进各区域林业TFP增长的主要来源，技术效率对TFP增长的贡献有限。其中，东北、中部和西部地区的林业TFP增长均表现出明显的技术进步单因素推进模式，技术效率恶化严重阻碍了TFP获得更快增长。尤其是作为传统林业大省的东北3省地区，林业技术效率恶化最为显著，年均下降3.61%。倘若其技术效率能够维持一种正增长趋势(大于1)，那么该地区的林业TFP增长将有望达到甚至超过东部地区。东部地区林业TFP增长表现出技术进步与技术效率改善共同作用的“双驱动”增长特征。结合前面的分析，从促进TFP增长的角度出发，这种“双驱动”模式将是未来中国林业保持可持续发展的关键。因此，东部地区的林业增长模式应努力成为未来各区域林业发展的方向。这就要求其他区域在充分发挥林业技术进步对TFP增长的“长板”作用的同时，更要重视对现有前沿技术的有效推广、扩散和利用，补齐林业技术效率水平低下这一“短板”。

3 结论与建议

本文在规模报酬不变的假定下，运用Malmquist生产率指数与随机前沿函数模型相结合的方法，对中国大陆30个省(市、自治区)2004—2015年的林业技术效率及林业TFP增长率进行再测算，结果发现： 1) 中国林业生产过程中存在比较普遍的技术无效现象，平均技术效率只有0.546，提升潜力巨大； 2) 年降水量、森林病虫鼠害发生面积和防治面积、林业专业技术人员数是造成省际林业技术效率差异的主要因素； 3) 2004—2015年，中国林业TFP实现了较快增长，年均增长16.48%，但这一增长主要由林业技术进步所贡献，林业技术效率水平低下且长期处于恶化状态对TFP产生了负面影响； 4) 在省际层面，与全国整体情况类似，各省份林业TFP增长主要依靠技术进步驱动，有一半以上省份的林业技术效率处于恶化状态，大大弱化乃至抵消了技术进步对TFP的正效应； 5) 分区域来看，东北、中部和西部地区的林业TFP增长均表现为技术进步与技术效率相背离的“单驱动”增长模式，只有东部地区呈现技术进步与技术效率改善共同作用的“双驱动”增长模式。

从促进TFP增长的角度出发，未来中国林业理想的增长模式应当是东部地区这种前沿技术进步与技术效率改善并存的“双驱动”模式。但过去10多年里，中国林业推广体系在前沿技术扩散上的相对失败，直接导致了全国大部分省份林业技术效率的恶化。因此，为实现“两条腿走路”，今后政府除了要继续加大林业科技投入、促进林业技术进步、发挥技术创新的“长板”作用外， 更为重要的是要加强对现有技术的推广应用，补齐林业技术效率水平低下这一“短板”。本文对各省及全国林业TFP增长来源的分解也表明，通过改善技术效率来促进林业TFP获得更快增长是完全可行的。基于此，结合模型分析中森林病虫鼠害防治面积、林业专业技术人员数对林业技术效率提升的重要作用，提出如下政策建议： 一是明确林业工作站的公益性定位，完善政府财政投入机制，充分发挥其在林业科技推广中的带头作用； 二是深化林业科技特派员制度，广泛动员和鼓励林业科技人员开展科技下乡、科技入户等活动； 三是建立健全林业科技推广员资格制度，提高各级推广机构中林业专业技术人员的比例； 四是加强重点病虫害的科研攻关和技术推广，研究推广新的林业有害生物防治技术，提高森林病虫鼠害防治水平。

陈向华，耿玉德，于学霆，等. 2012. 黑龙江国有林区林业产业全要素生产率及其影响因素分析.林业经济问题，32(1): 50-53.

(Chen X H, Geng Y D, Yu X T,etal. 2012. The analysis of the total factor productivity and its influencing factors of forest industry in state-owed region in Heilongjiang Province. Issues of Forestry Economics, 32(1): 50-53. [in Chinese])

陈晓兰，姜雪梅. 2014. 中国林业全要素生产率分析.林业经济，(3): 75-82.

(Chen X L, Jiang X M. 2014. A study on total factor productivity of Chinese forestry. Forestry Economics, (3): 75-82. [in Chinese])

傅晓霞，吴利学. 2007. 前沿分析方法在中国经济增长核算中的适用性.世界经济，(7): 56-66.

(Fu X X, Wu L X. 2007. Competing methods for efficiency measurement of China: a comparison of SFA vs DEA. Journal of World Economy, (7): 56-66.

黄安胜，刘振滨，许佳贤，等. 2015. 多重目标下的中国林业全要素生产率及其时空差异.林业科学，51(9): 117-125.

(Huang A S, Liu Z B, Xu J X,etal. 2015. Forestry total factor productivity under multiple targets in China and its spatiotemporal differences. Scientia Silvae Sinicae, 51(9): 117-125. [in Chinese])

李谷成，冯中朝，占绍文. 2008. 家庭禀赋对农户家庭经营技术效率的影响冲击——基于湖北省农户的随机前沿生产函数实证.统计研究，(1): 35-42.

(Li G C, Feng Z C, Zhan S W. An empirical analysis about the effect of household endowments on the technical efficiency of farmer’s household management: evidence from the farmers of Hubei Province. Statistical Research, (1): 35-42. [in Chinese])

李京华，包庆丰. 2016. 内蒙古国有林区林业全要素生产率分析.林业经济，(2):83-87.

(Li J H, Bao Q F. 2016. Analysis of total factor productivity of forest industry in state-owned forest region in Inner Mongolia. Forestry Economics, (2): 83-87. [in Chinese])

刘 璨，于法稳. 2006. 东北国有林区企业效率测算与分析——DEA方法.产业经济评论，5(1): 107-121.

(Liu C, Yu F W. 2006. Efficiency analysis of the northeast national forest enterprise: DEA approach. Review of Industrial Economics, (1): 113-127. [in Chinese])

刘清泉，江 华. 2014. 可持续发展视角下林业全要素生产率及影响因素——来自广东的证据.农村经济，(1):39-43.

(Liu Q Q，Jiang H. 2014. The total factor productivity of the forestry and its influencing factor based on the perspective of sustainable development: proof of the Guangdong. Rural Economy, (1): 39-43. [in Chinese])

马天乐，刘 璨. 1992. 中国林业总要素生产率测度与分析.林业经济，(4): 46-53.

(Ma T L, Liu C. 1992. Calculation and analysis of the total factor productivity of Chinese forestry. Forestry Economics, (4): 46-53. [in Chinese])

史常亮，朱俊峰，揭昌亮. 2016. 中国农业全要素生产率增长地区差异及收敛性分析——基于固定效应SFA模型和面板单位根方法.经济问题探索，(4): 134-141.

(Shi C L, Zhu J F, Jie C L. 2016. Regional difference and convergence analysis of agricultural TFP in China: on fixed-effect panel SFA and panel unit root. Inquiry into Economic Issues, (4): 134-141. [in Chinese])

宋长鸣，向玉林. 2012. 林业技术效率及其影响因素研究——基于随机前沿生产函数.林业经济，(2): 66-70.

(Song C M，Xiang Y L. 2012. Study of forestry industry technical efficiency and its influencing factor: based on stochastic frontier production function model. Forestry Economics, (2): 66-70. [in Chinese])

田 杰，姚顺波. 2013. 中国林业生产的技术效率测算与分析.中国人口·资源与环境，23(11): 66-72.

(Tian J, Yao S B. 2013. Research on technical efficiency of forestry production in China. China Population, Resources and Environment, 23(11): 66-72. [in Chinese])

田 杰，张晓棠，姚顺波. 2015. 考虑自然因素投入的林业生产效率评价研究——以南方集体林区为例. 西安工程大学学报，35(5): 378-386.

(Tian J, Zhang X T, Yao S B. 2015. Study on efficiency of forestry production based on the natural factors: a case of southern collective forest area. Journal of Xi’an Technological University, 35(5): 378-386. [in Chinese])

田淑英，许文立. 2012. 基于DEA模型的中国林业投入产出效率评价.资源科学，34(10): 1944-1950.

(Tian S Y, Xu W L. 2012. Evaluation of China’s forestry input-output efficiency based on DEA modeling. Resources Science, 34(10): 1944-1950. [in Chinese])

魏远竹，朱永法. 2001. 产业结构调整与林业经济增长方式转变.北京林业大学学报，23(1): 72-75.

(Wei Y Z, Zhu Y F. 2001. The adjustment of industrial structure and transformation of forestry economic growth pattern. Journal of Beijing Forestry University, 23(1): 72-75. [in Chinese])

吴延瑞. 2008. 生产率对中国经济增长的贡献： 新的估计.经济学(季刊)，(2): 827-842.

(Wu Y R. 2008. The role of productivity in China’s growth: new estimates. China Economic Quarterly, 7(3): 827-842. [in Chinese])

徐 玮，冯 彦，包庆丰. 2015. 中国林业生产效率测算及区域差异分析——基于Malmquist-DEA模型的省际面板数据.林业经济，(5): 85-88.

(Xu W, Feng Y, Bao Q F. 2015. China’s forestry production efficiency calculation and the analysis of regional difference: based on Malmquist-DEA model provincial panel data. Forestry Economics, (5): 85-88. [in Chinese])

臧良震，支 玲，郭小年. 2014. 中国西部地区林业生产技术效率的测算和动态演进分析.统计与信息论坛，29(1): 13-20.

(Zang L Z, Zhi L, Guo X N. 2014. Research on calculation and dynamic evolution of forestry production technical efficiency in Western China. Statistics & Information Forum, 29(1): 13-20. [in Chinese])

周子桥，全 良，刘慧妍. 2015. 基于生态产出和决策者偏好的黑龙江省林业全要素生产率研究.林业经济，(5): 93-99.

(Zhou Z Q, Quan L, Liu H Y. 2015. A study of total factor productivity in Heilongjiang forestry region based on ecological output and preference of decision maker. Forestry Economics, (5): 93-99. [in Chinese])

Battese G E, Coelli T J. 1995. A model for technical inefficiency effects in a stochastic frontier production function for panel data. Empirical Economics, 20(2): 325-332.

Berger A N, Humphrey D B.1997. Efficiency of financial institutions: international survey and directions for future research. European Journal of Operational Research, 98(2): 175-212.

Coelli T J, Perelman S. 2000. Technical efficiency of European railways: a distance function approach. Applied Economics, 32(15):1967-1976.

Färe R, Grosskopf S, Norris M,etal. 1994. Productivity growth, technical progress, and efficiency change in industrialized countries. American Economic Review, 84(1): 66-83.

Fuentes H J, Grifell-Tatjé E, Perelman S. 2001. A parametric distance function approach for Malmquist productivity index estimation. Journal of Productivity Analysis, 15(2):79-94.

Grifell-Tatjé E, Lovell C A K. 1995. A note on the Malmquist productivity index. Economics Letters, 47(2): 169-175.

Helvoigt T L, Adams D M. 2009. A stochastic frontier analysis of technical progress, efficiency change and productivity growth in the Pacific Northwest sawmill industry. Forest Policy and Economics, 11(4): 280-287.

Hseu J S, Shang J K. 2005. Productivity changes of pulp and paper industry in OECD countries, 1991—2000: a non-parametric Malmquist approach. Forest Policy and Economics, 7(3): 411-422.

Korkmaz M. 2011. Productivity changes of forest enterprises in Turkey: a non-parametric Malmquist approach. African Journal of Agricultural Research, 6(28): 6189-6196.

Lee J Y. 2008. Application of the three-stage DEA in measuring efficiency: an empirical evidence. Applied Economics Letters, 15(1): 49-52.

Managi S. 2010. Productivity measures and effects from subsidies and trade: an empirical analysis for Japan’s forestry. Applied Economics, 42(30): 3871-3883.

Ray S C, Desli E. 1997. Productivity growth, technical progress, and efficiency change in industrialized countries: comment. American Economic Review, 87(5): 1033-1039.

Wang H J, Schmidt P. 2002. One-step and two-step estimation of the effects of exogenous variables on technical efficiency levels. Journal of Productivity Analysis,18(2): 129-144.

Zang L Z, Zhang C H, Xu D Y,etal. 2015. Research on temporal-spatial evolution of regional disparity of forestry total factor productivity in China. Advance Journal of Food Science & Technology, 9(5): 332-341.

Zhang D, Nagubadi R V. 2006. Total factor productivity growth in the sawmill and wood preservation industry in the United States and Canada: a comparative study. Forest Science, 52(5): 511-521.