例谈初中数学三类微课的设计与实施

于彬

摘 要：利用微课进行教学，可以激发学生自主学习的热情，从而起到事半功倍的效果.在数学教学中教师应该根据需要对教材内容进行开发和利用，设计微课，达到巩固知识、突破难点、构建网络等目的.

关键词：微课；三线合一；分式方程；数式运算

微课是运用信息技术，按照认知规律，呈现碎片化学习内容、过程及扩展素材的结构化数字资源，有教学时间短、主题突出、内容具体、针对性强、形式灵活等特点.利用微课进行教学，可以激发学生自主学习的热情，从而起到事半功倍的效果. 在教学中笔者根据需要对人教版义务教育教科书《数学》进行开发和利用，设计微课，达到巩固知识、突破难点、构建网络等目的.

一、鞏固知识类微课：“三线合一”自述

“等腰三角形（第1课时）”是八年级上册第十三章第三节的教学内容，该课利用前面刚刚学习的轴对称知识以及全等三角形的相关内容研究等腰三角形所具有的两个性质：“等边对等角”和“三线合一”.“等边对等角”教材进行重点介绍，也有例题跟进；而对于“三线合一”则在“等边对等角”的基础上进行简单介绍，而且也缺乏必要的针对性练习，因此笔者在实际教学中设计了如下微课，通过该微课对“三线合一”的文字语言、图形语言和符号语言进行重点介绍，起到良好的教学效果.

微课PPT截图见图1～图6.

【微课脚本】

同学们，你们好！我叫“三线合一”，是你们这节课刚刚认识的新朋友，初中阶段剩下的时间里，我会时时刻刻陪伴在你们的身边.

我是“等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合”的简写.别看我只有四个字，我的内涵却十分丰富，我包含三个命题：

等腰三角形底边上的中线平分顶角并且垂直于底边，符号语言表示为：在[△ABC]中，∵[AB=AC，BD=CD，∴∠BAD=∠CAD，AD⊥][BC]；

等腰三角形顶角的平分线平分底边并且垂直于底边，符号语言表示为：在[△ABC]中，∵[AB=AC，∠BAD=∠CAD，∴BD=CD，AD⊥][BC]；

等腰三角形底边上的高平分顶角并且平分底边，符号语言表示为：在[△ABC]中，∵[AB=AC， AD⊥BC，∴∠BAD=∠CAD， BD=CD.]

以上三个命题都是正确的，它们是同学们以后几何学习中证明线段相等、角相等、线段垂直的“利器”，表1是对“三线合一”相关语言的直观呈现.

等腰三角形为什么会有这么好的性质呢？因为它是轴对称图形，底边上的中线（顶角平分线、底边上的高）所在的直线就是它的对称轴.同学们进入九年级以后，在“圆”的学习中，还会认识一个和我有点“亲缘”关系的定理——垂径定理，其实这和“圆”也是轴对称图形是有关系的.同学们先和我“处”好关系吧，到时我会把它再隆重介绍给你们.再见！

二、突破难点类微课：分式方程的发展历史简介

“分式方程（第1课时）”是八年级上册第十五章第三节的教学内容，主要涉及分式方程的定义和简单分式方程（可化为一元一次方程）的解法.这其中“引导学生体会分式方程检验的必要性”是本节课的教学难点，于是笔者设计了如下微课，在微课中从人类对分式方程的认识过程入手，简单介绍人类对知识探究永无止境的精神，并通过相关数学史的引入，提升了学生对数学学习的兴趣，可以说起到“一箭双雕”的预设效果.

微课PPT截图见图7～图11.

【微课脚本】

同学们，我们利用一节课的时间初步掌握了分式方程的定义和解法，但是其在数学历史上的发展却经历了漫长的过程.

分式方程来源于人类对现实生活中实际问题的解决，比如“分十问题”和“分钱问题”，其最早的记载来自于中世纪意大利数学家斐波那契（Leonardo Fibonacci，约1170—1250）的《计算之书》一书.但是，此时的人们并没有意识到分式方程“无解”的可能，直到后来德国数学家利普希茨（R. Lipschitz，1832—1903）等数学家指出：零不能作除数，这时人们才对分式方程“无解”有了初步的认识.1882年，美国康奈尔大学的教授奥里佛（J. E. Oliver）等在他们编写的《代数》一书中初步讨论了分式方程的解法.1899年，美国宾夕法尼亚大学的教授费舍（G. E. Fisher）等在他们编写的《代数基础》一书中给出分式方程的一般解法：先通过移项使得分式方程的一边化为零，然后进行通分、化简，再通过令分式的分子等于零、分母不等于零来求解，至此分式方程“无解”的问题得到完美解决.

分式方程的“无解”问题从发现到解决经历1个世纪的漫长历程，希望同学们通过对分式方程的学习，特别是其发展历史的认识树立正确的数学观，初步体会数学家为数学的发展所做出的不懈追求以及永无止境的探索精神.

三、构建网络类微课：数式“加减乘除”运算大家族

“二次根式的加减（第1课时）”是八年级下册第十六章第三节的教学内容，该课是初中阶段数式运算的最后一部分，为了加深学生对初中阶段所学数式运算的认识（特别是它们之间的区别与联系），也为了帮助学生构建“前后一致，逻辑连贯”的知识体系和网络，笔者设计了如下微课，通过该微课对初中阶段所学的数式运算进行简单的总结，特别是一句“数学是一步一步向上走的”，引导学生切实体会到相关知识之间的联系与区别，为进入高中阶段继续学习相关数式运算打下了坚实的基础.

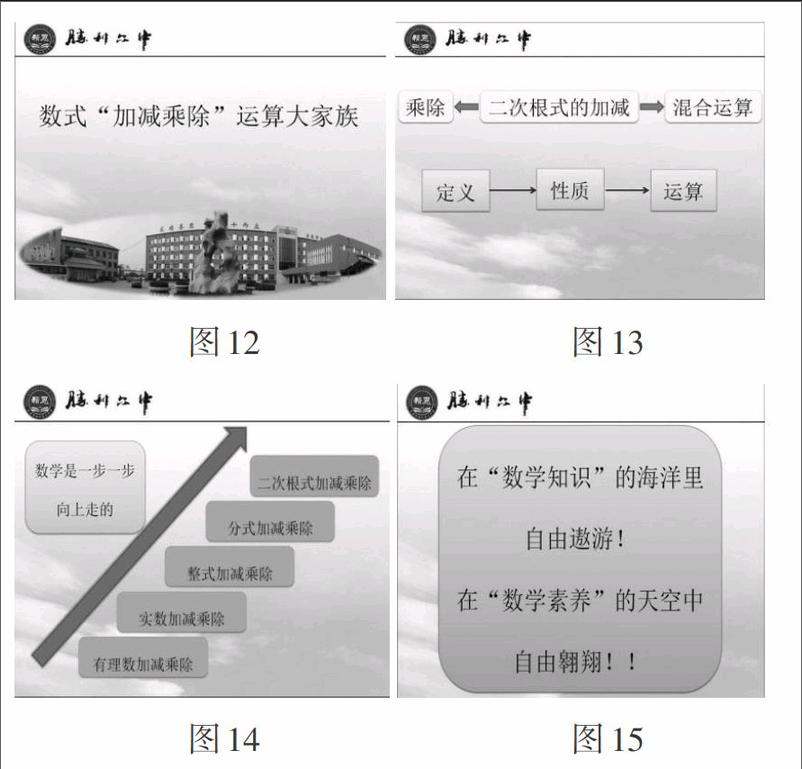
微课PPT截图见图12～图15.

【微课脚本】

同学们，通过本节课的学习我们初步掌握了二次根式加减运算的法则、一般步骤及运算依据，在前面我们还学习了二次根式的乘除运算，下节课我们还要学习二次根式的混合运算，希望同学们通过对二次根式的学习可以初步体会研究“数式”的“基本套路”：定义[→]性质[→]运算.

回过头来看一下，进入初中我们在七年级上册学习了有理数的加减乘除运算，七年级下册学习了实数的加减乘除运算，八年级上册分别学习了整式和分式的加减乘除运算，现在我们在八年级下册又学习了二次根式的加减乘除运算，至此我们在初中阶段需要学习的“数与式”的运算就要接近尾声了，希望同学们用心体会它们之间的区别与联系，比如整式的加减运算和二次根式的加减运算之间的联系：在整式加减运算适用的运算律在二次根式中同样适用；在二次根式的加减运算中我们把“被开方数相同的二次根式”进行合并和整式加减运算中的“合并同类项”是类似的，等等.

最后，把日本著名教育家、数学家米山国藏在其名著《数学的思想、精神及方法》中提到的一句话“数学是一步一步向上走的”送给同学们，以此共勉，期待同学们可以在“数学知识”的海洋里自由遨游，在“数学素养”的天空中自由翱翔.

微课之微主要在于其时间短，上述三个微课的时间都控制在两分钟之内，其中还有一些动画效果，可以很好地吸引学生的“眼球”，让学生在短时间内可以多看几遍，从而加深学生对所学内容的认识；微课不微，通过上述的介绍可以看出，初中数学三类微课在巩固知识、突破难点、构建网络方面所发挥的重要作用，无论是在课内还是课外，学生通过对相关微课的学习，都可以激发学生自主学习的热情，从而起到事半功倍的效果.

当然，我们为此所做的具体教学实践还是初步的，欢迎更多的一线教师参与进来，设计出更多实用的微课，从而为实现高效的初中数学课堂教学贡献一份微薄的力量.[□][◢]endprint