复杂曲线回归分析及其应用
2018-01-15谷恒明胡良平
谷恒明,胡良平,2*
(1.军事医学科学院生物医学统计学咨询中心,北京 100850;2.世界中医药学会联合会临床科研统计学专业委员会,北京 100029*通信作者:胡良平,E-mail:lphu812@sina.com)
复杂曲线回归分析及其应用
谷恒明1,胡良平1,2*
(1.军事医学科学院生物医学统计学咨询中心,北京 100850;2.世界中医药学会联合会临床科研统计学专业委员会,北京 100029*通信作者:胡良平,E-mail:lphu812@sina.com)
本文目的是介绍曲线方程的两种拟合方法(即直线化法与直接拟合法)之间的区别。通过对一个实例中散点图为“S型曲线”的资料采用直线化法与直接拟合法拟合Logistic曲线回归方程,对所得到的拟合结果进行比较,发现基于粗估值再采用SAS中的NLIN过程直接拟合Logistic曲线回归方程,可以得到更精确的拟合效果。
非线性回归分析;Logistic曲线回归方程;迭代计算;相关指数
*Correspondingauthor:HuLiangping,E-mail:lphu812@sina.com)
1 概 述
1.1 问题的提出
本刊本期的前一篇文章《简单曲线回归分析及其应用》介绍了用曲线直线化的方法实现几个常用初等函数曲线的曲线回归或曲线拟合的方法。然而,人们可能会提出下面两个问题。问题一:曲线直线化方法与直接进行曲线拟合的效果一样吗?问题二:是否所有的函数曲线都可以通过曲线直线化构建曲线回归方程?
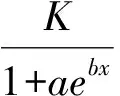
对第二个问题的回答也是否定的。其理由如下:事实上,能够通过直线化来实现曲线拟合的曲线类型是很少的,绝大多数函数曲线是无法通过简单直线化法来实现曲线拟合的。例如下面的两个函数曲线就无法通过直线化法进行曲线拟合。
二项型指数函数是由两个指数函数项相加而构成的函数表达式。此函数表达式所描绘出的曲线称为二项型指数曲线,见式(1)。
y=A×eαt+B×e-βt
(1)
又例如:三项型指数函数是由三个指数函数项相加而构成的函数表达式。此函数表达式所描绘出的曲线称为三项型指数曲线。此曲线常用于研究三室模型药物静脉注射或二室模型药物血管外给药后血药浓度与时间的关系,见式(2)。
y=Ne-kx+Le-αx+Me-βx
(2)
1.2 解决方案
SAS软件提供了NLIN和NLMIXED过程,可用于非线性曲线的拟合。但在拟合时需要读者给出未知参数的初始值。若初始值偏离真实值较远,则可能拟合过程无法收敛或拟合曲线并非最优。所以,较为合适的方法是通过曲线直线化求出参数的粗估值,然后将其作为初始值引入NLIN或NLMIXED过程进行迭代计算,以寻找拟合效果更好的曲线回归方程。然而,对于类似上面的式(1)和(2)那样无法实施直线化的函数方程式,估计参数的粗估值可能就带有很大的盲目性了。具体如何实现,请参见相关参考文献[1-2]。
由于直接进行曲线拟合问题难度较大,再考虑到文章篇幅有限,故本文仅介绍一个最常用的曲线拟合的实例。
2 实例解析
2.1 问题与数据
【例1】某研究者欲分析某县疟疾发病的季节性特点,观测了某县1961年-1996年疟疾的月累计发病率(1/10万),结果见表1。试对该资料进行曲线拟合。

表1 某县疟疾月累计发病率
2.2 如何用SAS实现计算
【分析与解答】图1散点图显示,资料的趋势近似S型曲线,故可采用Logistic曲线方程拟合此资料。曲线上限为130,下限为0,上下渐近线之间的垂直间隔为130,SAS程序如下:
%let ul=130; /*1*/
dataabc; /*2*/
do x=1 to 12;
input y@@;
z=log((&ul-y)/y);
output;
end;
cards;
0.555 1.295 2.751 11.116
24.879 43.476 69.297 97.037
114.631 121.645 124.412 125.619
;
run;
ods html;
proc gplot; /*3*/
plot y*x/haxis=0 to 12 vaxis=0 to &ul by 10;
symbol value=dot;
run;
proc reg data=abc outest=est(keep=Intercept x);
model z=x; /*4*/
run;quit;
data set1; /*5*/
set est;
call symput('a1',exp(Intercept));
call symput('b1',x);
run;
proc nlin data=abc; /*6*/
parms K=&ul a=&a1 b=&b1;
model y=K/(1+a*exp(b*x));
output out=set2 p=yp r=resid;
run;
proc sql; /*7*/
create table set3 (sum num,css
num);
insert into set3 select
1.人力资源配置优化。成立区域检修公司,通过统一调度检修人员,可以解决区域公司内部检修人员工作量不均衡,同时解决单个企业检修维护部组建人员和技术力量不足的问题。
sum(resid**2),css(y) from set2;
quit;
data set4; /*8*/
set set3;
r2=1-sum/css;
run;
proc print data=set2 round; /*9*/
run;
proc print data=set4; /*10*/
run;
ods html close;
【程序说明】程序中第1步是设立宏变量ul,表示曲线的上、下渐近线的垂直间距,其值为130,以便于后面调用。第2步是创建数据集,x表示月份,y表示疟疾月累计发病率,z是对y进行logit变换所得的变量,以便后面进行曲线直线化分析。第3步是绘制散点图,以发现散点分布趋势,本资料散点趋势近似S型曲线。第4步对变量z和x进行直线回归分析,将所得直线的截距和斜率保存在数据集est中。第5步对数据集est进行操作,将以自然对数为底、以截距为指数的数值赋给宏变量a1,将斜率赋给宏变量b1。当然,也可直接将截距赋给宏变量a1,将斜率赋给宏变量b1,但第6步中model语句给出的曲线方程需改为“y=K/(1+exp(a+b*x))”。第6步是调用NLIN过程来拟合Logistic曲线,宏变量ul、a1、b1的值分别赋给变量K、a、b作为初值,并将所得曲线对各观测拟合的预测值及残差输出到数据集set2中,预测值以变量yp表示,残差以resid表示。第7步将数据集set2的内容输出到output窗口。第7步是调用sql过程,建立一个表set3,包括sum和css两个变量,然后将数据集set2中所有观测resid的平方和赋给set3中的sum变量,将set2中所有观测y变量的离均差平方和赋给css。第8步是对数据集set3进行操作,计算新的变量r2,即相关指数。第9步是将数据集set2的内容输出到output窗口,round选项用来指定数据最多保留两位小数。第10步是将数据集set4的内容输出到output窗口。
2.3 SAS输出结果及其解释
【主要输出结果及解释】

图1 y随x变化的散点图
图1是SAS程序绘制的散点图。可以看出,散点近似S型曲线趋势,上限为130,下限为0。

AnalysisofVarianceDependentVariable:zSourceDFSumofSquaresMeanSquareFValuePr>FModel1102.44535102.44535658.11<.0001Error101.556660.15567CorrectedTotal11104.00201

RootMSE0.39455R-Square0.9850DependentMean0.50213AdjR-Sq0.9835CoeffVar78.57356

ParameterEstimatesVariableDFParameterEstimateStandardErrortValuePr>|t|Intercept16.003770.2428324.72<.0001x1-0.846400.03299-25.65 <.0001
这是曲线直线化分析的结果,即变量z与x之间直线回归分析的结果。截距为6.00377,斜率为-0.8464,它们与0之间的差异均有统计学意义,检验统计量t值分别为24.72、-25.65,P均<0.0001。直线回归方程为z=6.00377-0.8464x,转换成y与x的关系,即为:y=130/(1+e6.00377-0.8464x)。此时,残差平方和为194.02219,相关指数R2=0.99740。

The NLIN Procedure Dependent Variable y Method: Gauss-Newton

NOTE: Convergence criterion met
Note: An intercept was not specified for this model
这是NLIN过程拟合曲线模型的有关信息。迭代方法为Gauss-Newton法,以K=130,a=405,b=-0.8464为初始值,迭代了5次,得到了收敛的结果。

SourceDFSumofSquaresMeanSquareFValueApproxPr>FModel376037.425345.811770.1<.0001Error919.38072.1534UncorrectedTotal1276056.8

ParameterEstimateApproxStdErrorApproximate95%ConfidenceLimitsK127.81.0737125.4130.2a394.665.1746247.1542.0b-0.88790.0263-0.9474-0.8284

ApproximateCorrelationMatrixKabK1.0000000-0.50866920.6148707a-0.50866921.0000000-0.9798514b0.6148707-0.97985141.0000000
这是NLIN过程拟合模型的结果。对模型的检验结果为F=11770.1,P<0.0001,说明所拟合的模型是有统计学意义的。模型的三个参数取值分别为:K=127.8,a=394.6,b=-0.8879。所以,本资料所拟合的Logistic曲线回归方程为:
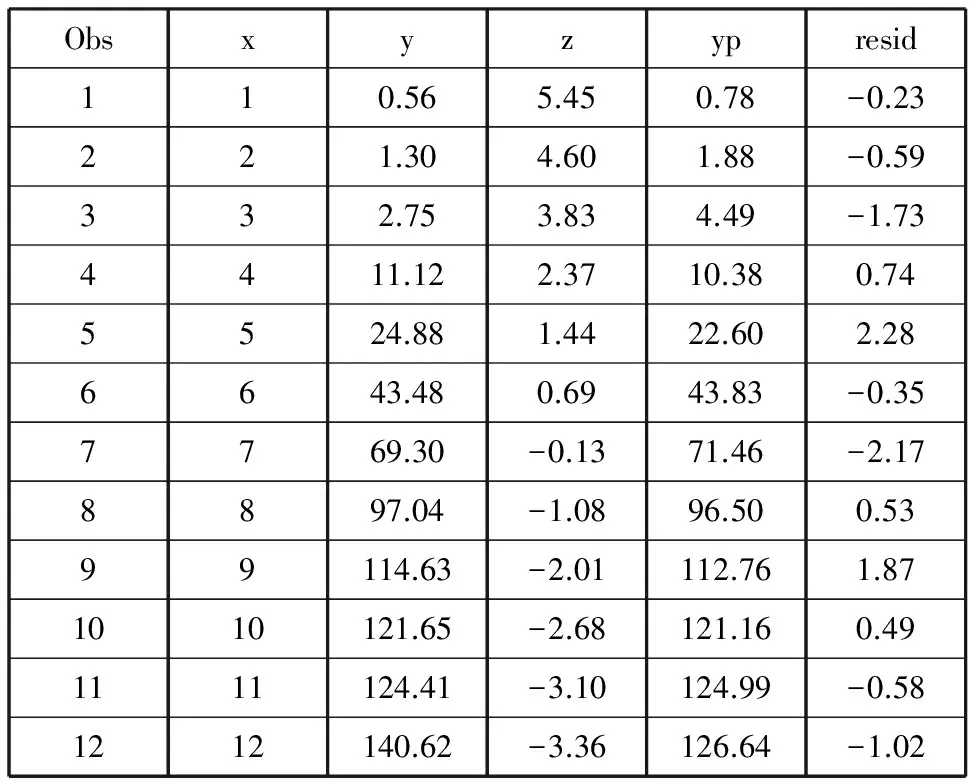
Obsxyzypresid110.565.450.78-0.23221.304.601.88-0.59332.753.834.49-1.734411.122.3710.380.745524.881.4422.602.286643.480.6943.83-0.357769.30-0.1371.46-2.178897.04-1.0896.500.5399114.63-2.01112.761.871010121.65-2.68121.160.491111124.41-3.10124.99-0.581212140.62-3.36126.64-1.02

Obssumcssr2119.380730827.910.99937
这是曲线拟合效果的结果。首先给出了曲线回归方程对各观测的拟合结果,yp列为曲线对各观测的预测值,resid为预测值与观测值之间的残差。然后给出了对拟合整体效果的评价情况,残差平方和为19.3807,相关指数R2=0.99937。
由此可知,在粗估值基础上直接进行Logistic曲线拟合,可获得更好的拟合效果。
[1] 胡良平, 高辉. 非线性回归分析与SAS智能化实现[M].北京: 电子工业出版社, 2013: 68-119.
[2] 胡良平. 科研设计与统计分析[M].北京: 军事医学科学出版社, 2012: 399-426.
Complexcurveregressionanalysisanditsapplication
GuHengming1,HuLiangping1,2*
(1.ConsultingCenterofBiomedicalStatistics,AcademyofMilitaryMedicalSciences,Beijing100850,China;2.SpecialtyCommitteeofClinicalScientificResearchStatisticsofWorldFederationofChineseMedicineSocieties,Beijing100029,China
The purpose of this paper is to introduce the difference between the two fitting methods (linearization and direct fitting) of curve equation. By fitting the Logistic curve regression equation with the linearized method and the direct fitting method for an example in which the scatter plot is "S-shaped curve". Compared the fitting results producing from the two methods mentioned above, it was found that the more accurate fitting result can be gotten by means of providing the crude estimators of the parameters in the regression equation and then directly fitting Logistic curve regression equation through the NLIN procedure in SAS/STAT.
Nonlinear regression analysis; Logistic curve regression equation; Iteration calculation; Correlation index
国家高技术研究发展计划课题资助(2015AA020102)
R195.1
A
10.11886/j.issn.1007-3256.2017.06.004
2017-12-03)
陈 霞)
