三角代数上理想包含图的自同构

陈莉

(中国矿业大学数学系,江苏徐州 221116)

1 引言

近几十年来,为了利用图的组合结构来研究环的代数结构,人们利用环上的两种代数运算定义了多种图,如环的零因子图、交换图、全图等,这些图的定义以及部分研究结果可以参考文献[1–9]等.众所周知环的许多性质与它的理想有着密切的关系.自然地,利用环的理想构造一些图,通过研究这些图的组合性质来刻画环的理想性质有着重要的意义.文献中相关的图有互极大图、理想交图、理想包含图等,这些图的研究可以参考文献[10–13]等.

在研究与环相关的图时,许多工作致力于研究图的一些参数,比如围长、直径、团数、色数等.这些参数可以揭示图的结构性质,环的性质以及它们之间的相互关系.另外,图的自同构是代数图论中一个重要的概念,它可以揭示图的顶点之间的关系以及图的对称性.但是正如文献[14]中所说,确定一个图的非平凡自同构不是一件容易的事.通过查阅文献,我们发现对于环上这些图,有关自同构的结果很少.我们只找到有关环上零因子图自同构的几个结果.对于环R,零因子图记为Γ(R),Aut(Γ(R))表示其上的自同构群.Anderson与Livinston[1]证明了对于非素整数n≥4,Aut(Γ(Zn))是对称群的直积.对于素数p和非交换环R=Mat2(Zp),Han[15]证明了Aut(Γ(R))⋍Sp+1.Park与Han[16]证明了对于有限域Fq上的二阶矩阵环R=Mat2(Fq),Aut(Γ(R))⋍Sq+1.但是最近文献[17]得出了下面的结论:Aut(Γ(M2(Fq)))的大小是((q−1)!)(q+1)2(q+1)!,并指出上面两篇文章中的结论是不对的.文献[18]与[20]进一步给出有限域上上三角矩阵环的零因子图的自同构刻画.

在文献[12]中,环R上的理想包含图In(R)定义为以R的非平凡左理想为顶点集,两个不同左理想I与J有一条边相连当且仅当IJ或JI;文献[12]中研究了图In(R)的连通性以及图的参数.设Fq为有限域,Fq上n×n阶上三角矩阵环记为R.文献[13]研究了环R上的理想关系图Γi(R),以R为顶点集,从A到B有一条有向边当且仅当IAIB,其中IA表示由A生成的双边理想,并确定了它的自同构.文献[12]与[13]中的图是有差别的,但都是利用理想的包含关系定义的图,所以可以统称为理想包含图.本文将文献[13]中的结果推广到上三角代数上,研究了有限域上分块上三角矩阵环上的理想包含图并给出了其上的自同构的描述.

设Fq为有限域,A为分块上三角矩阵,其中Aij(1≤i≤j≤r)为Fq上ni×nj矩阵.对于固定的正整数序列(n1,n2,···,nr),形如A的所有分块上三角矩阵记为B(q,(n1,n2,···,nr)),简记为B(q,r).我们称(n1,n2,···,nr)为B(q,r)的分块模式.在矩阵的常用运算下,B(q,r)是一个代数,称之上三角代数.

理想包含图In(B(q,r))是一个有向图,以B(q,r)为顶点集,从A到B有一条有向边,记为A→B,当且仅当IAIB,其中IA表示由A生成的双边理想.本文研究了B(q,r)中的理想,证明了B(q,r)为主理想环,并且给出了In(B(q,r))上自同构的描述.有限域Fq上的上三角矩阵是分块模式为(1,1,···,1)的分块上三角矩阵,因此文献[13]中的理想关系图是本文研究对象的一个特例.

本文的第二节、第三节分别给出B(q,r)中理想的刻画与理想包含图In(B(q,r))上自同构的刻画.

2 上三角代数中的理想

令S={(i,j)|1≤i≤j≤r}.文献[13]在S上定义了二元关系:(i1,j1)(i2,j2)当且仅当i2≤i1且j1≤j2.若(i1,j1)(i2,j2)且(i1,j1)/=(i2,j2),则记为(i1,j1)(i2,j2).子矩阵Aij所在的行集与列集分别记为Ni与Nj,且记(Ni,Nj)={(s,t)|s∈Ni,t∈Nj}.

定义2.1若A的子矩阵Aij满足:Aij/=0,且对于任意的(s,t)(i,j)有Ast=0,则称Aij为A的承块.记A的所有承块全体为supp(A).相应地,称(Ni,Nj)为A的承块区,记A的承块区全体为suppb(A).记(A)}以及

例2.2A是Z5上模式为(2,1,2,1)的分块上三角阵,

易见supp(A)={A11,A23,A34},{A11,A12,A13,A14,A23,A24,A34}.承块A11所在的区域为(N1,N1)={(1,1),(1,2),(2,1),(2,2)}.

显然,若 (s,t)∈(Ni1,Nj1),(s′,t′)∈(Ni2,Nj2)且 (i1,j1)(i2,j2),则有s′≤s且t≤t′;若Ai1j1与Ai2j2均是A的承块,则有i1/=i2,j1/=j2.

引理 2.3设A∈B(q,r)且suppb(A)={(Ni1,Nj1),(Ni2,Nj2),···,(Nim,Njm)}.

(i)若Akl则Akl=0;若(i,j)(k,l),Akl则Aij=0;

(ii)若i1＜i2＜···＜im,则j1＜j2＜···＜jm.

证 (i)的证明.若Akl/=0,则存在序对(i,j)满足(i,j)(k,l)且Aij∈supp(A),从而矛盾.结论的后半部分显然成立.

(ii)的证明.若存在序对(s,t)使得is＜it且js＞jt,则(it,jt)(is,js).由Aisjs为承块得Aitjt=0,这与Aitjt也是承块相矛盾.因此结论成立.

引理2.3对刻画B(q,r)的理想和主理想有重要的作用.

定义2.4若ik≤jk(1≤k≤m),1≤i1＜i2＜ ···＜im≤r且1≤j1＜j2＜ ···＜jm≤r,则称{(i1,j1),(i2,j2),···,(im,jm)}为[1,r]×[1,r]上的一个上三角阶梯.记[1,r]×[1,r]所有上三角阶梯的集合为uts(r).

由引理2.3知B(q,r)中任意非零元的承块区的指标集是一个上三角阶梯.记B(q,r)的双边理想全体为I(B(q,r)).对于A∈B(q,r),IA表示由A生成的主理想.A在s行、t列处的元素用Ast来表示.另外,用Est表示在s行、t列处的元素为1且其余元素均为0的矩阵.

引理2.5设I为B(q,r)的一个理想.若Est∈I且(s,t)∈(Ni,Nj),则对于任意的(i′,j′)满足 (i,j)(i′,j′) 以及任意的 (s′,t′)∈(Ni′,Nj′) 有Es′t′∈I.

证 由 (i,j)(i′,j′),(s,t)∈(Ni,Nj) 以及 (s′,t′)∈(Ni′,Nj′),得到s′≤s和t≤t′. 因此Es′s,Ett′∈B(q,r) 且Es′sEstEtt′=Es′t′,从而有Es′t′∈I.

命题2.6对于任意的A/=0∈B(q,r),IA=A,其中

证 首先证明对于任意的P,Q∈B(q,r)有PAQ∈A,从而有IAA.由分块阵的乘法知,PAQ∈B(q,r).而且对于1≤k≤l≤r,

设(Nk,Nl)∈/suppb(A),也就是Akl考察PAQ在分块区(Nk,Nl)处的子矩阵.当k≤s≤t≤l时,(s,t)(k,l).由引理2.3,Ast=0,因此有(PAQ)kl=0.由(Nk,Nl)的任意性,有PAQ∈A.

下面证明对于任意的 (Ni′,Nj′)以及 (s′,t′)∈(Ni′,Nj′),有Es′t′∈IA,进而有AIA. 由于 (Ni′,Nj′)所以存在 (i,j)≤ (i′,j′) 使得 (Ni,Nj)∈suppb(A).由(Ni,Nj)∈suppb(A)知存在(s,t)∈(Ni,Nj)满足ast/=0,从而有由引理 2.5 可得对于任意 (s′,t′)∈(Ni′,Nj′),Es′t′∈IA. 综上可得A=IA.

推论2.7存在B(q,r)的非零主理想与上三角阶梯uts(r)之间的一一对应.

证 由引理2.3知B(q,r)中任意非零元素承块区的指标集是一个上三角阶梯.同时显然对于每一个上三角阶梯,存在B(q,r)中非零元素使其以该上三角阶梯为承块区的指标集.另外由命题2.6知对于任意的A,B∈B(q,r),IA=IB当且仅当suppb(A)=suppb(B).因此结论成立.

设I为B(q,r)的一个理想.若存在(s,t)∈(Ni,Nj)使得Est∈I,则由引理2.5知对于任意的 (s′,t′)∈(Ni,Nj) 有Es′t′∈I.

定义2.8设I为B(q,r)的一个理想.若存在(s,t)∈(Ni,Nj)使得Est∈I,则称分块区(Ni,Nj)为I的内块区.I的所有内块区的集合记为Iin,它在全集{(Ni,Nj)|1≤i≤j≤r}下的补记为Iout. 若 (Ni,Nj)∈Iin且对于任意的 (i′,j′)(i,j) 有 (Ni′,Nj′)∈Iout,则称(Ni,Nj)为I的边界区.I的所有边界区的集合记为Ib.

若 (Ni,Nj)∈Iin且 (i,j)(i′,j′),由引理 2.5 知 (Ni′,Nj′)∈Iin. 对于子集Ni,令=max{s|s∈Ni}.若(Ni,Nj)∈Iin,则ENiMNjm∈I.为了方便,也简记为ENiNj.

命题2.9 B(q,r)为主理想环.

证 零理想是由零生成的.对于任意的非零理想I∈I(B(q,r)),由上面的讨论知

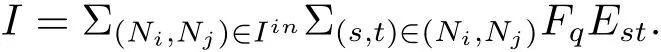
令A=Σ(Ni,Nj)∈IbENiNj.由边界区的定义和性质知Ib恰是A的承块区suppb(A),且容易看出从而由命题2.6得

推论2.10存在I(B(q,r))/{0}与uts(r)之间的一一对应.

证 由推论2.7以及命题2.9可得.

3 B(q,r)上的理想包含图及其上的自同构

理想包含图In(B(q,r))是一有向图,以B(q,r)为顶点集且从A到B有一条有向边A→B当且仅当IAIB.这里的理想包含图与文献[12]中的有些差别.在文献[12]中,环R上的理想包含图In(R),以R的所有非平凡的左理想为顶点,左理想I1和I2之间有一条边相连当且仅当I1I2或I2I1.因此文献[12]中理想包含图是无向的且顶点集是非平凡的左理想.我们所讨论的理想包含图In(B(q,r))是有向图且顶点集是B(q,r)中的所有元素.图In(B(q,r))的自同构群记为Aut(In(B(q,r))).

在图In(B(q,r))中,顶点A的左、右邻点集分别记为Nl(A)={B|B→A}与Nr(A)={B|A→B}.记di(A)=|Nl(A)|以及do(A)=|Nr(A)|,它们分别称为A的入度和出度.如果A与B在In(B(q,r))中具有相同的左、右邻点,则称A与B为孪生点,记为A∼B.若在图In(B(q,r))中,两个顶点生成相同的主理想,则它们显然是孪生点.容易验证孪生关系∼是B(q,r)上的一个等价关系,记A所在的孪生等价类为[A].我们知道图的自同构保持顶点的度以及等价类的大小不变,也就是,对于任意的σ∈Aut(In(B(q,r)))和A∈B(q,r),有di(σ(A))=di(A),do(σ(A))=do(A) 且|[σ(A)]|=|[A]|.

引理3.1在理想包含图In(B(q,r))中,下面的结论成立

(i)从A到B有有向边(A→B)当且仅当

(ii) 设r≥ 3. 对于任意的 1 ≤i≤j≤r,(s,t)∈(Ni,Nj) 以及 (s′,t′)∈(Ni′,Nj′),[Est]=[Es′t′]当且仅当 (i,j)=(i′,j′);

(iii)设r≥3且(s,t)∈(Ni,Nj).X～Est当且仅当suppb(X)={(Ni,Nj)}.

证 从命题2.6可以直接得到(i).

(ii) 的证明. 若 (i,j)=(i′,j′), 由推论 2.7 得到IEst=IEs′t′, 进而有 [Est]=[Es′t′]. 下面证明若 (i,j)/=(i′,j′), 则 [Est]/=[Es′t′]. 假定 (i,j)/=(i′,j′). 若 (i,j)(i′,j′), 则由命题 2.6 得IEs′t′IEst, 进而有Es′t′→Est. 但是EstEst, 因此 [Est]/=[Es′t′]. 如果(i′,j′)(i,j),可以类似的得到 [Est]/=[Es′t′]. 下面假定i＞i′且j＞j′. 若j/=r,则有ENiNr→Est, 但ENiNrEs′t′. 若j′/=1,则有Es′t′ →ENi′Nj′−1,但EstENi′Nj′−1. 若j=r且j′=1,由r≥ 3 知存在j′＜k＜j. 从而ENi′Nk→Es′t′,但是ENi′NkEst. 因此都有 [Est]/=[Es′t′]. 当i＜i′且j＜j′时,类似可得 [Est]/=[Es′t′].

(iii)的证明.若suppb(X)={(Ni,Nj)},则由命题2.6有IX=IEst,进而有X～Est.因此充分性成立.下面证明必要性.假定X～Est.若|supp(X)|=1,假设suppb(X)={(Ni′,Nj′)}并任取 (s′,t′)∈(Ni′,Nj′). 由推论 2.7 知,IX=IEs′t′. 从而 [X]=[Es′t′],进而有 [Est]=[Es′t′]. 由结论 (ii) 知 (i,j)=(i′,j′). 因此 suppb(X)=(Ni,Nj). 下面证明|supp(X)|不可能大于1.若|supp(X)|≥ 2,则对于任意的(Ni′,Nj′)∈suppb(X)以及(s′,t′)∈(Ni′,Nj′),有Es′t′ →X. 因此Es′t′ →Est,进而有 (i,j)(i′,j′). 由 (Ni′,Nj′) 的任意性,得到IXIEst,进而X→Est.但EstEst,与假定X～Est相矛盾.

推论3.2设r≥3以及1≤k≤r.对于任意的(s,t)∈(N1,Nk),|[Est]|=(qn1nk−对于任意的

证 由引理3.1的(iii)知对于任意的(s,t)∈(N1,Nk),

由此易见结论的前半部分成立,后半部分同理可得.

引理3.3对于理想包含图In(B(q,r))中顶点的度,下面的结论成立.

(i)di(0)=0;

(ii)任意(s,t)∈(N1,Nr),di(Est)=1;任意A∈B(q,r),di(A)=1当且仅当A～EN1Nr;

(iii)任意(s,t)∈(N1,Nk),di(Est)=其中1≤k≤r−1;任意(s,t)∈其中2≤k≤r;

(iv)任意A∈B(q,r),di(A)=qn1nr当且仅当A～EN1Nr−1或A～EN2Nr.

证 由引理3.1可得Nl(0)=Ø;任意的(s,t)∈(N1,Nr),Nl(Est)={0};任意的1 ≤k≤r−1 以及 (s,t)任意的2 ≤k≤r以及 (s,t)∈(Nk,Nr),Nl(Est)=显然,若A/=0,AEN1Nr,AEN1Nr−1且AEN2Nr,则有di(A)＞qn1nr.因此结论成立.

若双射σ:B(q,r)→B(q,r)只置换孪生点,则σ∈Aut(In(B(q,r))),这样的自同构称之为奇异自同构.图In(B(q,r))上奇异自同构的全体记为Sin(In(B(q,r))).

定理3.4图In(B(q,2))上的自同构都是奇异的.

证 当r=2,上三角阶梯utr(2)只有四种形式且对应的代表元可取

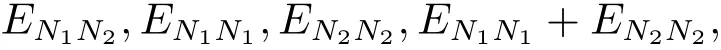
同时有di(0)=0;di(EN1N2)=1;di(EN1N1)=di(EN2N2)=qn1n2;di(EN1N1+EN2N2)＞qn1n2.另外在B(q,2)中,EN1N1～EN2N2.既然自同构保持顶点的度,从而In(B(q,2))上的自同构都是奇异的,即Aut(In(B(q,2)))=Sin(In(B(q,2))).

假设(n1,n2,···nr)为一正整数序列满足:对于任意的1≤k≤r都有nk=nr+1−k.定义映射τP:B(q,r)→B(q,r),对于任意的A∈B(q,r),τP(A)=PATP,其中P=AT表示A的转置.容易验证在假定条件下τP的定义是合理的且是一个双射.

命题3.5τP为图In(B(q,r))上的自同构.

证 假设从A到B有有向边,A→B.从而有IAIB,进而A∈IB.因此存在Q1,Q2∈B(q,r)使得A=Q1BQ2.从而有PATP=因此IPATPIPBTP.若IPATP=IPBTP,则PBTP∈IPATP.同上类似可得B∈IA,进而有IA=IB,与前提IAIB相矛盾.因此IPATPIPBTP,进而有τP(A)→τP(B).所以τP∈Aut(In(B(q,r))).

假设σ∈Aut(In(B(q,r)))(r≥3).为了刻画σ,需要揭示对于任意的A∈B(q,r),A与σ(A)之间的关系.

引理 3.6σ(0)=0;[σ(EN1Nr)]=[EN1Nr];[σ(EN1Nr−1)]=[EN1Nr−1]或 [σ(EN1Nr−1)]=[EN2Nr]且n1nr−1=n2nr.

证 从引理3.3,推论3.2以及σ保持顶点度以及孪生等价类大小,可得结论成立.

命题 3.7(i) 若 [σ(EN1Nr−1)]=[EN1Nr−1],则对于任意的 2 ≤k≤r−1,[σ(EN1Nr−k)]=[EN1Nr−k]成立;

(ii)若[σ(EN2Nr)]=[EN2Nr],则对于任意的3≤k≤r,[σ(ENkNr)]=[ENkNr]成立;

(iii)若 [σ(EN1Nr−1)]=[EN2Nr],则对于任意的 0 ≤k≤r−1,[σ(EN1Nr−k)]=[ENk+1Nr]且n1nr−k=nk+1nr.

证 (i)的证明.在假定条件下k=1时结论成立.下面证明若结论当k=t时成立,则当k=t+1时结论也成立.从而由归纳法知结论对于任意的k都成立.假定[σ(EN1Nr−t)]=[EN1Nr−t]. 由EN1Nr−t→EN1Nr−(t+1), 可得EN1Nr−t→σ(EN1Nr−(t+1)). 因此IEN1Nr−tIσ(EN1Nr−(t+1)). 由引理 2.3,存在 (Ni,Nj)∈suppb(σ(EN1Nr−(t+1))) 且 (i,j)(1,r−t).因此i≥ 1且j≤r−t.若i≥ 2或suppb(σ(EN1Nr−(t+1)))−{(Ni,Nj)}/=Ø,则有

从而有di(σ(EN1Nr−(t+1)))矛盾. 因此 suppb(σ(EN1Nr−(k+1)))={(N1,Nj)}.由di(σ(EN1Nr−(t+1)))=di(EN1Nr−(t+1))以及引理 3.3 可得j=r−(t+1),进而有

(ii)的证明.由[σ(EN2Nr)]=[EN2Nr]证明对于任意的1≤k≤r,[σ(ENkNr)]=[ENkNr]成立,可以类似于(i),省略.

(iii)的证明.由假定以及引理3.6知结论当k=0,1时成立.下面用归纳法来证明.假设结论当k=l时成立. 由 [σ(EN1Nr−l)]=[ENl+1Nr] 以及EN1Nr−l→EN1Nr−(l+1),可得ENl+1Nr→σ(EN1Nr−(l+1)). 因此IENl+1NrIσ(EN1Nr−(l+1)). 由命题 2.6知存在(Ni,Nj)∈suppb(σ(EN1Nr−(l+1)))且(i,j)(l+1,r).因此j≤r且i≥l+1.若j＜r且suppb(σ(EN1Nr−(l+1)))−{(i,j)}/=Ø,则但是由引理3.3知道di(EN1Nr−(l+1))

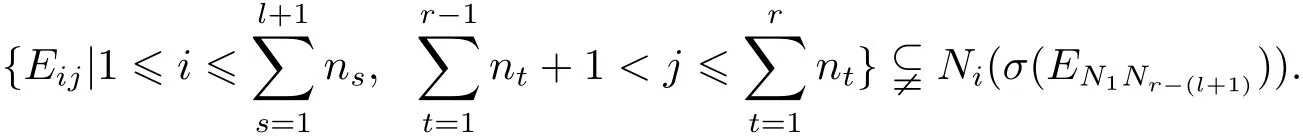
因此di(σ(EN1Nr−(l+1)))再由归纳假设知n1(nr+···+nr−l)=(n1+···+nl+1)nr, 从而有di(σ(EN1Nr−(l+1)))=矛盾.因此 suppb(σ(EN1Nr−(l+1)))={(Ni,Nr)}.再由引理 3.3 可得i=l+2,进而有 [σ(EN1Nr−(l+1))]=[ENl+2Nr].

最后,由σ保持孪生类大小知|[EN1Nr−(l+1)]|=|[ENl+2Nr]|.再由推论3.2知

由归纳假设知n1nr−(l+1)=nl+2nr.因此当k=l+1时结论也成立.由归纳法知结论对于任意的0≤k≤r−1都成立.

定理3.8假定r≥3.对于σ∈Aut(In(B(q,r))),存在奇异自同构ρ∈Sin(In(B(q,r)))和δ∈{0,1}使得σ=τδP◦ρ.

证 由引理 3.6 知,σ(0)=0;[σ(EN1Nr)]=[EN1Nr];[σ(EN1Nr−1)]=[EN1Nr−1] 或[σ(EN1Nr−1)]=[EN2Nr].首先证明存在δ∈{0,1}使得σ1=τδP◦σ稳定任意的[ENiNj](1≤i≤j≤r).分两种情况来讨论.

情形 1[σ(EN1Nr−1)]=[EN1Nr−1].

由引理3.6和命题3.7知,对于任意的1≤k≤r有[σ(EN1Nk)]=[EN1Nk].下面证明[σ(EN2Nr)]=[EN2Nr]也成立,进而由命题3.7知对于任意的1≤k≤r有[σ(ENkNr)]=[ENkNr]. 由引理 3.3 知,[σ(EN2Nr)]=[EN2Nr] 或 [σ(EN2Nr)]=[EN1Nr−1].若 [σ(EN2Nr)]=[EN1Nr−1], 由EN1Nr−1→EN1Nr−2且 [σ(EN1Nr−2)]=[EN1Nr−2], 可得σ(EN2Nr)→σ(EN1Nr−2),从而得到EN2Nr→EN1Nr−2,这显然是不可能的.因此[σ(EN2Nr)]=[EN2Nr].

下面证明对于任意的1≤i≤j≤r,[σ(ENiNj)]=[ENiNj]成立.对i做归纳证明.当i=1时结论成立;假设当1≤i−1≤j≤r时结论成立,下面证明当1＜i≤j≤r时结论也成立.为此对j再做归纳证明.由上面的讨论知当j=r时结论是成立的;假定当1＜i≤j+1≤r时结论成立.由ENi−1Nj→ENiNj,ENiNj+1→ENiNj,[σ(ENi−1Nj)]=[ENi−1Nj]且 [σ(ENiNj+1)]=[ENiNj+1], 可以得出ENi−1Nj→σ(ENiNj) 且ENiNj+1→σ(ENiNj). 由EN1Nj−1ENiNj,ENi+1NrENiNj,[σ(EN1Nj−1)]=[EN1Nj−1]且 [σ(ENi+1Nr)]=[ENi+1Nr],可以得出EN1Nj−1σ(ENiNj)且ENi+1Nrσ(ENiNj).因此σ(ENiNj)～ENiNj或σ(ENiNj)～ENi−1Nj+ENiNj+1.但是容易验证di(ENi−1Nj+ENiNj+1)＜di(ENiNj).因此σ(ENiNj)～ENiNj.令σ1=τδP◦σ且此时δ=0.

情形 2[σ(EN1Nr−1)]=[EN2Nr].

由命题3.7知对于任意的0≤k≤r−1有[σ(EN1Nr−k)]=[ENk+1Nr]且n1nr−k=nk+1nr;令σ1=τP◦σ,则有 [σ1(EN1Nr)]=[EN1Nr]且 [σ1(EN1Nr−1)]=[EN1Nr−1]. 由情形 1 知[σ1(ENiNj)]～[ENiNj](1≤i≤j≤r).此时σ1=τδP◦σ且δ=1.

下面证明σ1稳定任意的孪生等价类,即对于任意的A∈B(q,r),有[σ1(A)]=[A].

假定A/=0 且suppb(A)={(Ni1,Nj1),(Ni2,Nj2),···,(Nim,Njm)}.若m=1,则[A]=[ENi1Nj1].因此[σ1(A)]=[A].若m≥ 2,由ENikNjk→A以及[σ1(ENikNjk)]=[ENikNjk]可得ENikNjk→σ1(A). 因此IENikNjkIσ1(A). 令由命题2.6得IA=IX⊆Iσ1(A).同样的考虑的作用,可以得出对于任意的A∈B(q,r)有Iσ1(A)⊆IA.因此Iσ1(A)=IA,进而有 [σ1(A)]=[A].

令ρ=σ1,则ρ∈Sin(In(B(q,r))).进而有结论得证.

推论3.9假定r≥3.若存在1≤k≤r满足nk/=nr+1−k,则图In(B(q,r))上的每一个自同构均是奇异的.

证 假设存在1≤k≤r使得nk/=nr+1−k.由定理3.8的证明过程可得,对于任意的σ ∈Aut(In(B(q,r))),有[σ(EN1Nr−1)]=[EN1Nr−1].进而对于任意的A∈B(q,r)有[σ(A)]=[A],即σ∈Sin(In(B(q,r))).所以Aut(In(B(q,r)))=Sin(In(B(q,r))).

[1]Anderson D F,Livinston P S.The zero-divisor graph of a commutative ring[J].J.Alg.,1999,217:434–447.

[2]Redmond S P.The zero-divisor graph of a non-commutative ring[J].Intern.J.Commut.Rings,2002,1(4):203–211.

[3]Akbari S,Mohammadian A.Zero-divisor graphs of non-commutative rings[J].J.Algebra,2006,296:462–479.

[4]Akbari S,Ghandehari M,Hadian M,Mohammadian A.On commuting graphs of semisimple rings[J].Linear Alg.Appl.,2004,390:345–355.

[5]Abdollahi A.Commuting graphs of full matrix rings over finite fields[J].Linear Alg.Appl.,2008,428:2947–2954.

[6]Mohammadian A.On commuting graphs of finite matrix rings[J].Commun.Alg.,2010,38:988–994.

[7]Anderson D F,Badawi A.The total graph of a commutative ring[J].J.Alg.,2008,320:2706–2719.

[8]Akbari S,Kiani D,Mohammadi F,Moradi S.The total graph and regular graph of a commutative ring[J].J.Pure Appl.Alg.,2009,213:2224–2228.

[9]Akbari S,Aryapoor M,Jamaali M.Chromatic number and clique number of subgraphs of regular graph of matrix algebras[J].Linear Alg.Appl.,2012,436:2419–2424.

[10]Sharma P K,Bhatwadekar S M.A note on graphical representation of rings[J].J.Alg.,1995,176:124–127.

[11]Chakrabarty I,Ghosh S,Mukherjee T K,Sen M K.Intersection graphs of ideals of rings[J].Disc.Math.,2009,309:5381–5392.

[12]Akbari S,Habibi M,Majidinya A,Manaviyat R.The inclusion ideal graph of rings[J].Comm.Alg.,2015,43:2457–2465.

[13]Ma X B,Wong D.Automorphism group of an ideal-relation graph over a matrix ring[J].Linear Multi.Alg.,2016,64:309–320.

[14]Godsil C,Royle G.Algebraic graph theory[M].New York:Springer-Verlag,2001.

[15]Han J.The zero-divisor graph under group actions in a noncommutative ring[J].J.Korean Math.Soc.,2008,45(6):1647–1659.

[16]Park S,Han J.The group of graph automorphisms over a matrix ring[J].J.Korean Math.Soc.,2011,48(2):301–309.

[17]Ma X B,Wang D Y,Zhou J M.Automorphisms of the zero-divisor graph over 2×2 matrices[J].J.Korean Math.Soc.,2016,53(3):519–532.

[18]Wong D,Ma X B,Zhou J M.The group of automorphisms of a zero-divisor graph based on rank one upper triangular matrices[J].Linear Alg.Appl.,2014,460:242–258.

[20]Wang L.A note on automorphisms on the zero-divisor graph of upper triangular matrices[J].Linear Alg.Appl.,2015,465:214–220.

[20]Chen M X,Chen Q H.The automorphisms of triangular algebras[J].J.Math.,2010,30(4):587–594.