智能仓储机器人全局定位方法研究

2018-01-15张伟忠江苏苏州国家粮食储备库有限公司

食品安全导刊 2017年36期

□ 张伟忠江苏苏州国家粮食储备库有限公司

文章首先对混沌粒子群优化算法及粒子滤波方法存在的缺陷进行了简单介绍，继而对混沌粒子群优化算法与粒子滤波融合计算方法进行详细阐述，最后通过仿真实验的方式证明，利用混沌粒子群优化算法可有效改善粒子滤波，提升智能仓储机器人全局定位效率，值得在实践中推广使用。

表1 三种方法仿真实验滤波性能比较

前言

全局定位技术是研发智能仓储机器人的一项关键技术，在应用过程中对精度的要求较高。为进一步提升智能仓储机器人全局定位的精度，本研究通过仿真实验的方式，探究利用混沌粒子群优化算法改善粒子滤波的效果，以下为具体研究内容。

混沌粒子群优化算法及粒子滤波方法缺陷分析

粒子群优化算法是目前十分先进的一种进化计算技术，鸟群的捕食行为是其基础原型。本研究拟采用混沌粒子群优化算法弥补粒子滤波方法存在的缺陷。在保障粒子集收敛性的基本原则不变的前提下，通过将混沌扰动机制引入其中，利用混沌遍历性和随机性提升粒子的遍历性以及种群的多样性，从而持续为速度放缓粒子提供搜寻可行解的能力。

子滤波方法的理论基础为贝叶斯滤波原因，本质上为一种利用系统模型预测状态的先验概率密度，继而通过对已知观测数据进行进一步的修正，从而获取后验概率密度的一种方法。子滤波方法存在的主要缺陷集中在两个方面，其一为粒子本身缺乏，其二为实际效率较低，极易导致预估计的失败。

混沌粒子群优化算法与粒子滤波融合计算方法

首先，混沌粒子群优化算法可基于自身的自适应能力改变权重值，均衡混沌粒子群优化算法的局部搜索能力以及全局搜索能力，继而提升粒子的收敛速度，避免粒子陷入局部最优的困境中，从而实现在较短的时间内完成全局的精准定位。粒子滤波方法则是自身通过不断更新粒子的位置和权重值的方式，最大限度逼近系统真实后验概率的分布情况。然后，在混沌粒子群优化算法中具备最适应度值的粒子即最优值点的粒子，在粒子滤波方法中则是系统中最有可能状态粒子所具备的一个最大权重值。最后，在混沌粒子群优化算法和粒子滤波方法内都存在着彼此的运行机制。在粒子滤波方法中，粒子自身会基于运动模型更新自己的位置，然后再通过观测模型的方式实现自身权重值的更新。在混沌粒子群优化算法中的每个粒子则是通过个体最优和全局最优值的方式，来不断实现位置和速度的更新。

仿真实验

仿真设计

本研究设计了如公式1、公式2所示的粒子滤波方法和混沌粒子群优化算法与粒子滤波融合计算方法比较系统，将其置于不同噪声环境下的一维非线性系统中进行仿真实验。

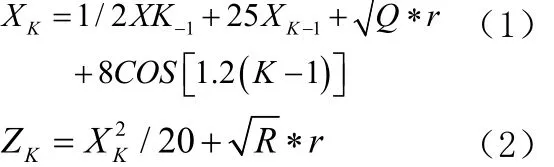
其中，r取值为(0,1)，噪声方差R=1，过程噪声方差Q=10。在仿真实验的过程中，粒子数目选择500，迭代次为100，时间步长取50。均方根误差计算公式如公式（3）所示：

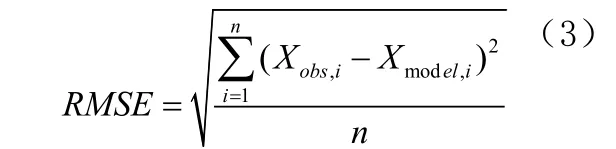
将两者置于相同的情况之下，期望估算的精度越高，则均方根误差越小。选择标准状态对仿真结果进行估计，从混沌粒子群优化算法与粒子滤波融合计算方法的估算效果可知，其效果要明显优于粒子群优化算法与粒子滤波融合计算方法和粒子滤波方法。表1为具体的仿真实验数据，可见混沌粒子群优化算法与粒子滤波融合计算方法在均方根误差以及运行时间方面都具备更大的优势。

实验结果

将混沌粒子群优化算法与粒子滤波融合计算方法具体应用到智能机器人的全局定位中，同时将粒子滤波方法、粒子群优化算法与粒子滤波融合计算方法置于同条件下进行实验对比。在实验的过程中，设定机器人在周期环境信息的感知上使用SICK二维激光传感器。观察实验结果可知，混沌粒子群优化算法与粒子滤波融合计算方法可以十分快速地收敛到机器人在其实际中的位置周围。粒子群优化算法与粒子滤波融合计算方法的表现则相对较差，传统的粒子滤波方法的实验结果显示，不能在很短的时间内实现收敛，甚至还出现了轻微的发散情况，可见混沌粒子群优化算法与粒子滤波融合计算方法对于智能仓储机器人的全局定位具有很好的效果。