基于微多普勒信息的弹道目标成像

夏 鹏,田西兰

(1.中国电子科技集团公司第三十八研究所,安徽合肥230088;2.孔径阵列与空间探测安徽省重点实验室,安徽合肥230088;3.智能情报处理重点实验室,安徽合肥230088)

0 引言

随着弹道导弹突防手段的不断提升,反导目标识别技术成为弹道导弹防御系统最为关键的技术之一,对导弹防御系统的成败起着决定性的作用。作为防御系统最为重要的预警探测装备,雷达在弹道目标识别中发挥着至关重要的作用。近年来,微多普勒效应成为了目标特性分析与识别领域的研究热点,基于微多普勒特征的目标识别技术已被认为是雷达目标识别技术最具发展潜力的技术之一[1]。基于弹头微动特性识别弹头的关键是对微多普勒的精确估计和提取,一种方法是建立弹头目标回波模型,进行目标特性参数的估计[2-5];另一种方法是对目标回波信号进行时频分析,在时频图基础上提取各类稳健特征进行识别[6-9]。

为充分利用目标回波的微动信息,有必要对弹头目标进行成像,这对目标表征与识别具有重要意义。传统的逆合成孔径雷达(Inverse Synthetic Aperture Radar,ISAR)成像因微运动形式的复杂性而较难获得满足识别要求的图像。针对上述问题,本文提出一种基于微多普勒信息的弹头目标成像方法,即利用目标散射中心瞬时频率的变化实现对目标二维分布的重构。第1节建立弹道目标滑动散射中心模型,并详细分析了弹道目标回波调制规律;第2节介绍基于微多普勒信息的弹道目标成像方法;第3节采用滑动散射中心模型仿真数据及电磁计算数据进行验证,实验结果证实了本文方法的有效性。

1 弹道目标滑动散射中心模型

散射中心是雷达目标在光学区等效的散射源,目标结构上的散射源由于不同的散射机理等效为不同类型的散射中心。理想散射中心模型认为散射中心的位置及其散射强度不随入射电磁波频率和方位的变化而变化。对于旋转对称的弹头目标而言,理想散射中心模型不能够准确反映目标真实散射情形,散射中心所处的位置与雷达回波入射面和目标之间的相对位置密切相关。下面以光滑对称圆锥目标为例,介绍弹道目标滑动散射中心的进动微多普勒模型。

弹道目标进动模型如图1所示。为方便建立目标的微动方程,设参考坐标系为(X,Y,Z),其坐标原点O位于目标质心,目标坐标系为(x,y,z),原点与参考坐标系相同。设目标底面半径为r,高度为L,半锥角为α,质心O距底面距离为h,雷达视线(Line of Sight,LOS)与目标中轴夹角为β(t),LOS与目标进动轴OZ夹角为γ,目标中轴与进动轴夹角为θ。

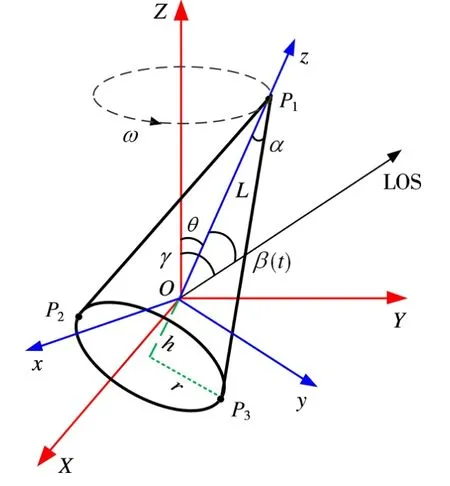
图1 弹道目标进动模型

由文献[10]可知,对于平底锥弹头来说,一般认为有3个强散射中心,分别是目标顶部P1及底面边缘上的两点P2,P3(LOS与目标对称轴组成的平面与目标底面边缘的两个交点)。其中顶点P1为理想散射中心,底部散射中心P2,P3为滑动散射中心。t时刻,根据余弦定理,顶点P1与雷达之间的距离为

由于L-h≪R0,则有

从图1可以看出,滑动散射中心位置是由LOS和目标中轴指向共同决定的。将散射中心P2,P3往雷达视线上投影,则散射中心距雷达距离变化R2(t),R3(t)分别为

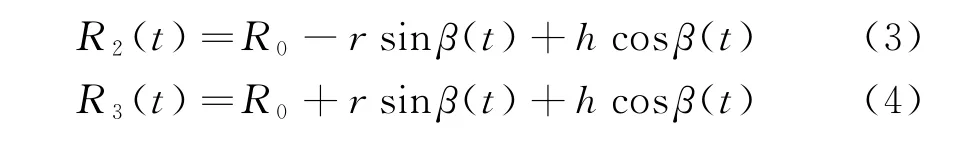
对于该目标,LOS与目标中轴夹角β(t)变化关系为

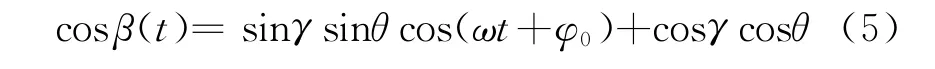
对式(2)、式(3)及式(4)求导即可得到各散射中心微多普勒频率变化:

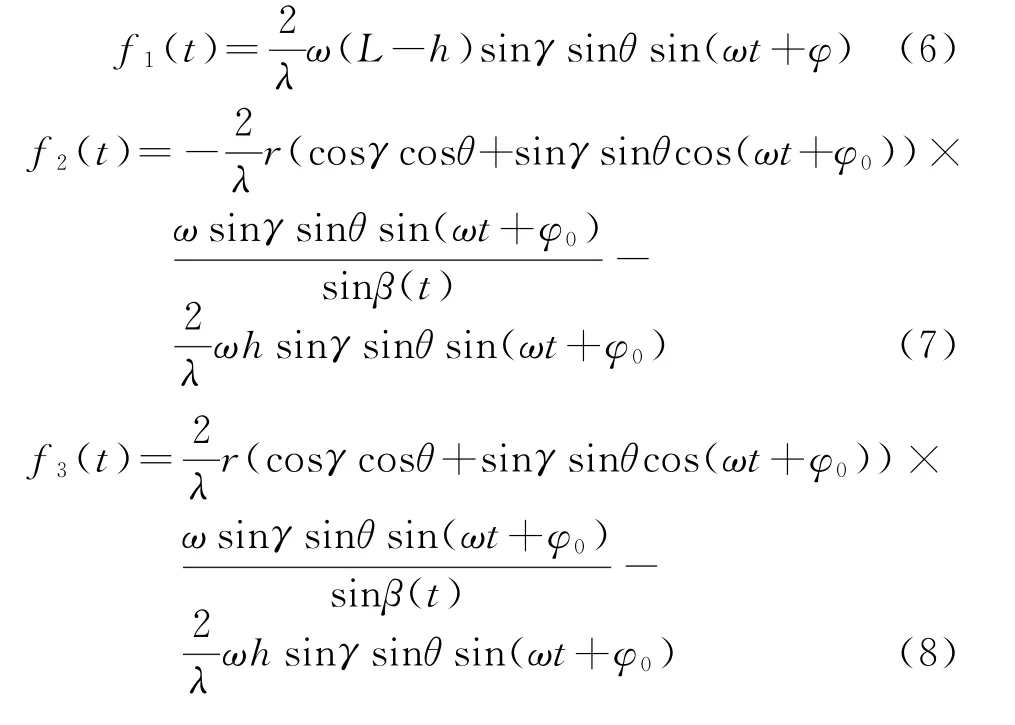
2 基于微多普勒信息的弹道目标成像方法

为便于分析,如图2所示,引入u-v坐标系,并与x-y坐标系逆时针成θ角,两组坐标系之间的变换关系为

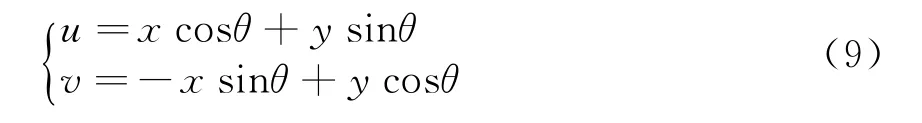
在固定角度θ上,目标二维分布函数f(x,y)在u-v坐标系中沿v轴投影可表示为

对式(10)进行傅里叶变换:

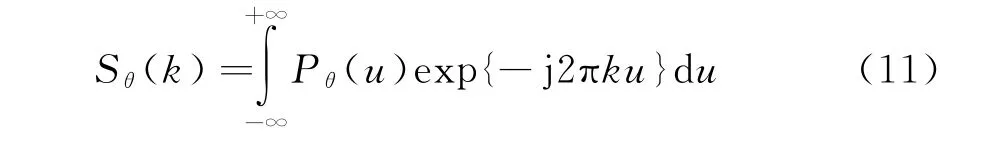
将式(10)代入式(11)中得到

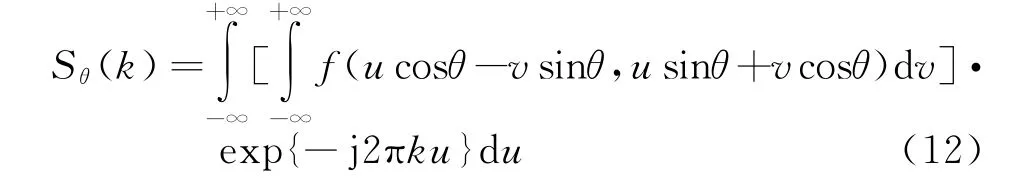
利用式(9)的关系将式(12)转换到x-y坐标系:

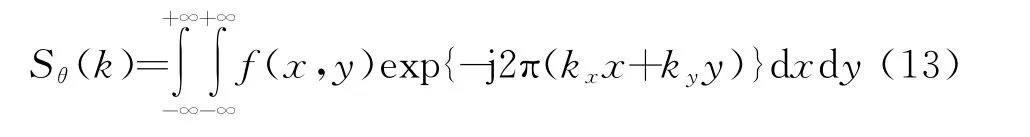
式中,kx=kcosθ,ky=ksinθ表示空间频率。式(13)右边表示目标二维分布函数f(x,y)的二维傅里叶变换,于是得到关系:

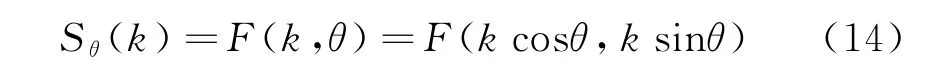
式(14)表明,目标二维分布函数f(x,y)的二维傅里叶变换在kx-ky平面上过坐标原点且沿某一方向的直线上的值正好对应函数f(x,y)沿同一方向上投影函数的一维傅里叶变换值。

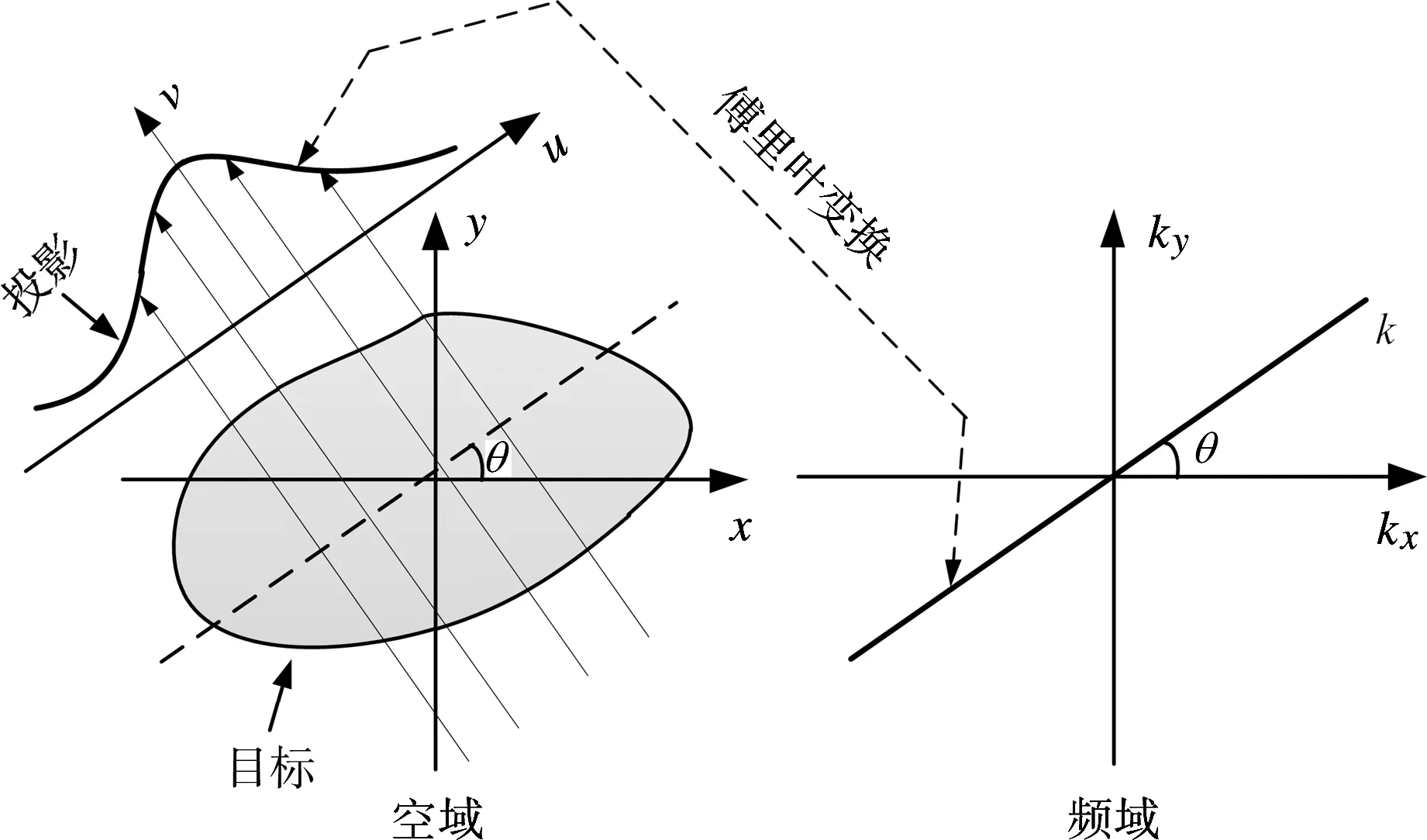
图2 微多普勒成像示意图

弹道目标瞬时频率随时间呈正弦规律变化,其信号的理想时频分布为包含正弦曲线的二维图像,因此投影数据可通过对微多普勒信号进行时频分析获取。当获得大量的投影数据后,便获得了目标函数f(x,y)在二维傅里叶平面上的取样值F(kx,ky),给定F(kx,ky),目标函数f(x,y)即可通过二维逆傅里叶变换进行重构。

3 仿真实验

设雷达工作在X波段,中心频率f0=10 GHz,雷达重复频率PRF=500 Hz。目标电磁计算模型如图3所示,设目标高度L=1 m,底面半径r=0.25 m,质心距底面距离h=0.15 m,目标自旋频率为0.8 Hz,锥旋频率为1 Hz,锥旋角θ=10°,积累时间为2 s。

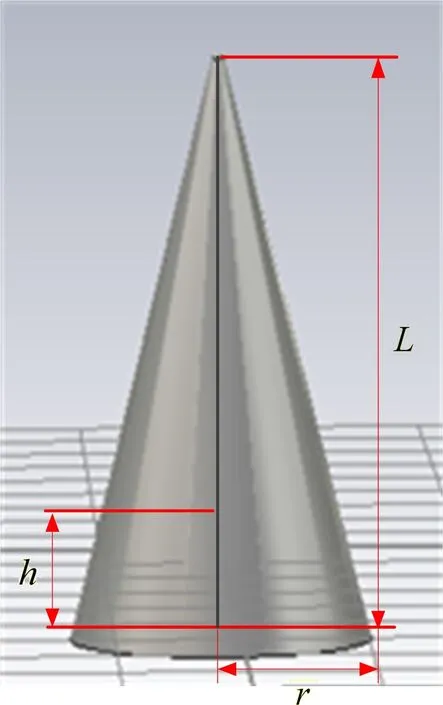
图3 弹道目标电磁计算模型

由仿真参数可知,目标半锥角α=0.254 8 rad,LOS与目标中轴夹角β(t)随时间变化情况如图4所示,可以看出α＜β(t)＜π/2,因此散射点P3处于遮挡状态[11]。

图4 LOS与目标中轴夹角变化情况

图5(a)给出了由式(6)～式(8)确定的两个散射点微多普勒频率随时间变化的理论曲线,其中点P1由于位于自旋轴上,微动形式仅包括锥旋,因此对应的微多普勒频率随时间的变化曲线为正弦曲线形式;底部边缘散射中心P2微多普勒曲线偏离了余弦函数形式,造成这种现象的原因是非理想的散射中心并不固定,而是沿着目标的轮廓滑动,散射中心的微运动规律与目标整体的微运动规律并不完全一致。回波微多普勒信号的时频分析结果如图5(b)所示,与理论曲线十分吻合。由图5(b)可以看出,每条正弦曲线对应着散射点的微多普勒变化规律,对该时频图进行成像处理,得到散射点的二维分布,如图5(c)所示,可以看出,目标散射中心清晰地显现出来。

图5 弹道目标滑动散射中心模型仿真结果

进一步采用电磁计算数据对文中方法进行验证,其中图6(a)为微多普勒信号时频分析结果,可以看出,等效散射点模型得到的散射点瞬时频率结果与电磁计算数据的结果吻合得很好,这也说明了本文建立的等效散射点模型的正确性。图6(b)为基于电磁计算数据成像结果,可以看出,目标散射中心清晰地显示了出来。

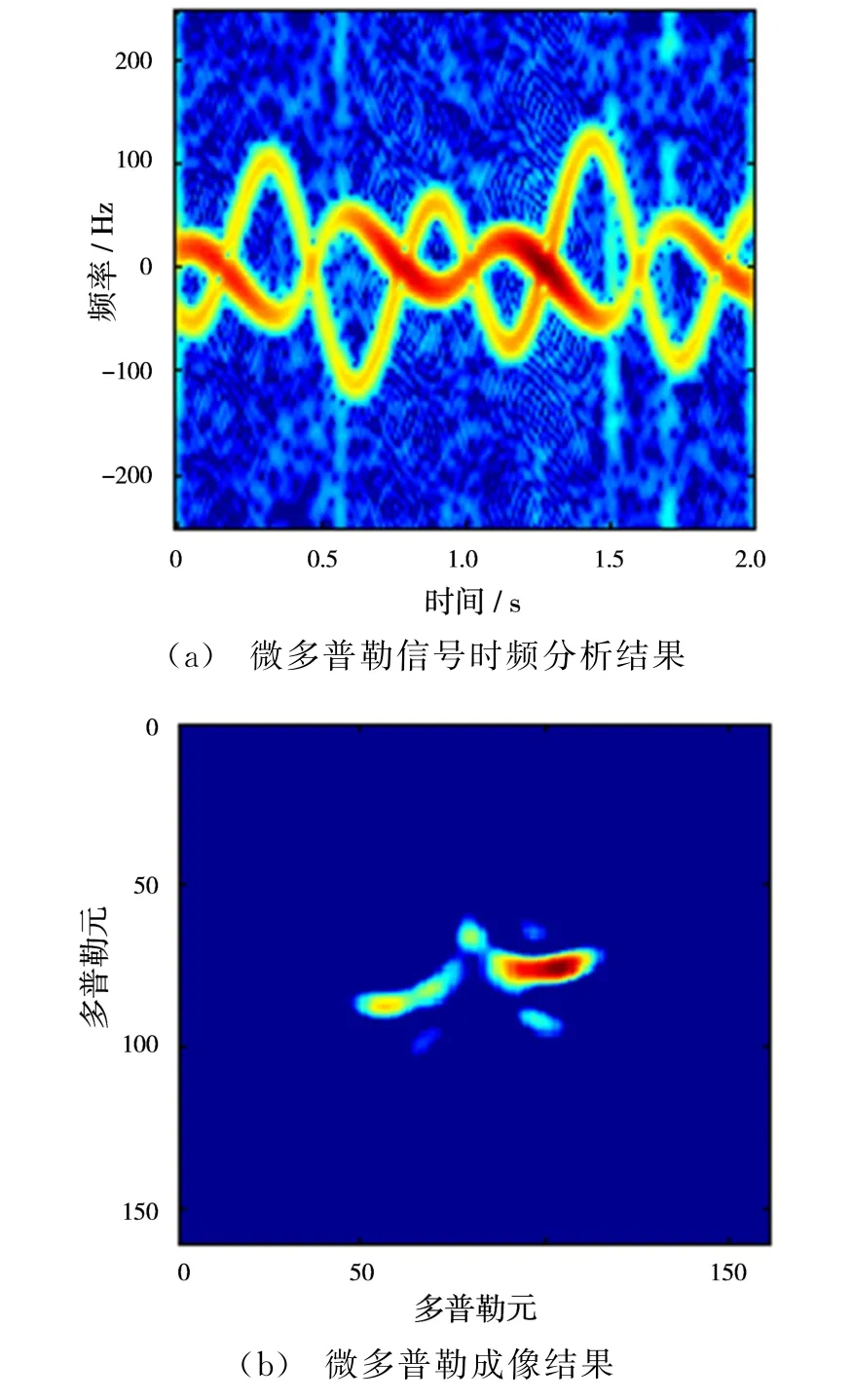
图6 电磁计算数据处理结果

4 结束语

微动对雷达目标主回波的调制蕴含了目标丰富的特征信息。本文在建立弹道目标滑动散射中心模型的基础上,对弹道目标的微动效应进行了详细分析,提出了利用微多普勒信息重建目标二维像的方法,通过滑动散射中心模型仿真数据及电磁计算数据对所提方法进行了验证,实现了弹道目标散射中心二维分布重建。后续将结合微波暗室数据及外场实测数据对算法的有效性进一步验证。

[1]张群,罗迎.雷达目标微多普勒效应[M].北京:国防工业出版社,2013:1-10.

[2]韩勋,杜兰,刘宏伟.基于窄带微多普勒调制的锥体目标参数估计[J].电子与信息学报,2015,37(4):961-968.

[3]ZHANG Wenpeng,LI Kangle,JIANG Weidong.Pa-rameter Estimation of Radar Targets with Macro-Motion and Micro-Motion Based on Circular Correlation Coefficients[J].IEEE Signal Processing Letters,2015,22(5):633-637.

[4]LEI Peng,SUN Jinping,WANG Jun,et al.Micromotion Parameter Estimation of Free Rigid Targets Based on Radar Micro-Doppler[J].IEEE Trans on Geoscience and Remote Sensing,2012,50(10):3776-3786.

[5]李彦兵,张曦文,李飞,等.一种大加速度机动目标微动参数估计方法[J].电子与信息学报,2017,39(1):82-87.

[6]秦晓东,张仕元,喻荣梅.基于时间分段数据的弹道目标微多普勒时频分析方法[J].空军预警学院学报,2015,29(4):255-257.

[7]邓冬虎,张群,罗迎,等.Duffing振子在低信噪比雷达目标微动特征提取中的应用[J].电子与信息学报,2014,36(2):453-458.

[8]LIU Yongxiang,ZHU Dekang,LI Xiang,et al.Micromotion Characteristic Acquistion Based on Wideband Radar Phase[J].IEEE Trans on Geoscience and Remote Sensing,2014,52(6):3650-3657.

[9]黎耿,黎向阳,张军.要地警戒雷达目标特征提取及分类研究[J].雷达科学与技术,2016,14(2):127-133.LI Geng,LI Xiangyang,ZHANG Jun.Target Feature Extraction and Classification in Warning Radar at Strategic Point[J].Radar Science and Technology,2016,14(2):127-133.(in Chinese)

[10]黄培康,殷红成,许小剑.雷达目标特性[M].北京:电子工业出版社,2005:86-92.

[11]曹文杰,张磊,杜兰,等.基于瞬时频率估计的进动锥体目标微多普勒频率提取方法[J].电子与信息学报,2015,37(5):1091-1096.