基于多种奖励机制的囚徒困境博弈模型研究

囚徒困境博弈模型作为演化博弈经典模型成为近年来的研究热点，针对规则格子网络中如何提高囚徒困境博弈的合作水平问题，我们引入奖励因子来促进参与者采取合作策略。为了研究奖励因子对网络中所有个体采取合作或背叛策略的影响，并探究奖励因子针对不同奖励对象时对规则网络中囚徒博弈合作水平的影响，我们引入3种奖励机制：只奖励合作者；只奖励背叛者；对整个网络中的所有个体都奖励。我们在Matlab平台上进行仿真实验，看到奖励因子会明显提高网络整体的合作水平，并找到其原因，是因为奖励因子对合作者的影响要高于对背叛者的影响，使得当都有相同背叛获利b值时，网络整体合作水平会随着奖励因子的增加而升高，网络中所有个体更趋向于合作而不是背叛。

自1950年Nash所做出的开创性工作以来，博弈成为了一门系统理论，并被广泛应用到人类社会，特别是经济行为当中。作为一门交叉研究学科，在复杂网络中的演化博弈成为现在的关注热点之一。囚徒困境博弈模型作为演化博弈经典模型之一，研究其在规则网络中演化更是重中之重[1-5]。

现实中利己者间出现的自发合作行为及其维持机制得到了越来越多的关注[6-7]，将演化博弈理论与复杂网络的结合也成为了一个热点[8-9]。在复杂网络的演化博弈中，通常以网络中的节点作为个体，使用规则格子网络表示一般性人际关系网络，为了有效地促进参与者采取合作策略，在囚徒困境博弈模型中引入奖励因子，在网络中的个体进行策略学习时，我们改变其收益函数，使得下一轮的收益出现变动，从而探究这种变动对博弈模型合作水平的影响。本文将基于“奖励”机制，在引入奖励因子的概念，又探究奖励因子针对不同奖励对象对规则网络中囚徒博弈合作水平的影响。

本文首先阐述囚徒困境博弈模型及规则网络模型的构建，并将具体阐述本研究所采用的模型及其收益矩阵、奖励因子；其次进行实验仿真，并利用Matlab实现模型的构建与仿真实验；最后给出研究结论。

模型

囚徒困境博弈模型

在博弈中，每个个体都有几种策略，个体会从这些策略中选出一种以使自己获得最大的收益[10]，并且每个人都是理性的。囚徒困境是两个被捕的囚徒之间的一种特殊博弈，其说明了为什么甚至在合作对双方都有利时，保持合作也是困难的。在囚徒困境博弈模型中，每个个体都有两种策略选择：合作C（Cooperation）、背叛D（Defection）。如A、B两个个体进行博弈时，会出现四种情况：如果个体A采取背叛D策略，个体B采取合作C策略，那么个体A的收益为T，个体B的收益为S；如果A、B双方都采取合作C策略，那么双方均获得利益为R；如果A、B双方都采取背叛D策略，那么双方均获得收益为P。即收益矩阵E为：

且对于囚徒困境博弈，有如下规则：T>R>P>S，且2R>T+S。在囚徒困境博弈中，两个个体需要同时决定他们各自的策略。

为了方便研究，简化收益矩阵中参数的数目，我们使用Weak-PD模型，即采用Nowak和May使用的收益矩阵E：

在本文中，我们考虑PD博弈模型为Weak-PD博弈模型，且令1

方格子网络模型

本文采用100×100具有周期边界条件的方格子网络，即存在10 000个个体，如图1所示。其中，黄色圆圈表示网络中的个体，数字为个体标号，黑色线表示网络中个体与个体之间的连接关系，蓝色虚线方框内为100×100方格子网络，蓝色虚线方框外侧表示该网络所具有的周期边界条件。因为为方格子网络，则每个个体有四个邻居。

引入奖励因子

分析收益矩阵，如果两个个体进行一次博弈，个体为了达到自己收益最大化，都会选择背叛策略。但是为了提高整体的合作水平，需要采取某种“奖励”措施来促进个体采取合作策略，从而有利于合作策略的涌现和维持。在这里我们引入文献[11]中的奖励因子规则，对网络中的个体进行收益上的奖励。为了便于研究不同奖励机制对规则网络中囚徒困境博弈合作水平的影响，我们维持一个稳定的记忆长度M。

Matlab仿真及结果分析

Matlab是将计算矩阵、分析数值、数据可视化以及非线性动力学系统的建模和仿真等诸多强大功能集成在一起的强大软件。本文利用Matlab软件进行仿真，过程为：在图1所示的方格子网络中进行博弈；初始网络中全部10 000个个体的初始策略，在这里我们采用随机赋值初始条件法；设定MCS为1×104；由于初始条件为随机初始条件，为了消除随机误差，我们做了100次系综平均。

在本文中，我们将奖励机制分为3种：1）只奖励合作者；2）只奖励背叛者；3）对整个网络中的所有个体都奖励。

如图2所示，a为只奖励合作者、b为只奖励背叛者、c为同时奖励时，奖励因子分别取

通过比较图2中a、b、c三图，我们可以发现，选择不同的奖励机制，对网络中整体的合作水平的影响也不同。如果只奖励合作者，当都有相同背叛獲利b值时，网络整体的合作水平会随着奖励因子的增加而增加，网络中的个体更趋向于合作；如果只奖励背叛者，当都有相同背叛获利b值时，网络整体合作水平会随着奖励因子的增加而降低，网络中的个体更趋向于背叛；如果对整个网络中所有个体都奖励，当都有相同背叛获利b值时，网络整体合作水平呈现出随着奖励因子的增加而升高，即可以说明奖励因子对合作者的影响要高于对背叛者的影响，使得网络中所有个体更趋向于合作，这也是奖励因子可以提高网络整体合作水平的原因。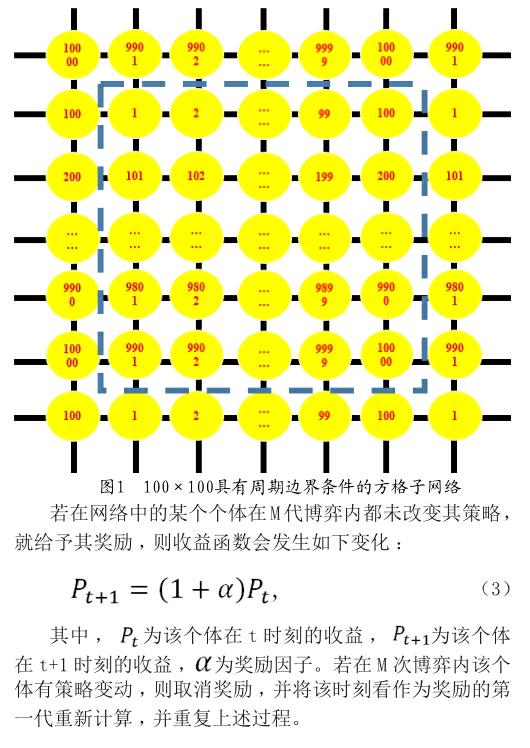

总结与展望

本文建立一个基于奖励因子的囚徒困境博弈模型，在网络中个体博弈过程中，根据个体所采取的策略不断更新其收益，使得个体在更新策略时考虑奖励因子对个体学习过程的影响。我们看到奖励因子会明显提高网络整体的合作水平，并发现奖励因子对合作者的影响要高于对背叛者的影响，导致网络整体合作水平会随着奖励因子的增加而升高，网络中所有个体更趋向于合作而不是背叛。该结论对奖励因子提高博弈合作水平的原因有了更全面的解读。

参考文献

[1]SANTO FORTUNATO. UNIVERSALITY OF THE THRESHOLD FOR COMPLETE CONSENSUS FOR THE OPINION DYNAMICS OF DEFFUANT et al.[J].International Journal of Modern Physics C，2004，15（9）：1301-1307.

[2]王文旭.复杂网络的演化动力学及网络上的动力学过程研究[D].合肥：中国科学技术大学，2007.

[3]代琼琳.复杂网络上的演化博弈动力学研究[D]北京：北京邮电大学，2011.

[4]杨志虎.复杂网络上的演化博弈与合作演化动力学研究[D].西安：西安电子科技大学，2014.

[5]李燕.空间囚徒困境博弈中合作解的演化[D].杭州：浙江大学，2017.

[6]廖列法，孙玮，刘朝阳.基于演化博弈研究移动和噪声对合作的影响[J].计算机应用与软件，2015（3）：53-56.

[7]刘华，李莹，赵建立，等.沉默策略对囚徒困境博弈合作水平的影响[J].数学的实践与认识，2016，46（20）：240-247.

[8]宋亦泠，王秉中，朱洪，等.重复囚徒困境的学习和响应模型[J].计算机工程与科学，2007，29（10）：115-119.

[9]劉贞，任玉珑，唐松林.基于Mealy自动机的重复囚徒困境博弈模型[J].管理科学，2006，19（5）：66-70.

[10]Doebeli M，Hauert C.Models of cooperation based on the Prisoners Dilemma and the Snowdrift game[J].Ecology Letters，2005，8（7）：748-766.

[11]陈维春，尚丽辉.基于奖励因子的囚徒困境博弈模型研究[J].电子科技，2016，29（3）：5-6.

（作者简介：唐宸，重庆市第八中学校。）endprint