基于网络熵的银行系统稳定的影响因素研究

李智+牛晓健

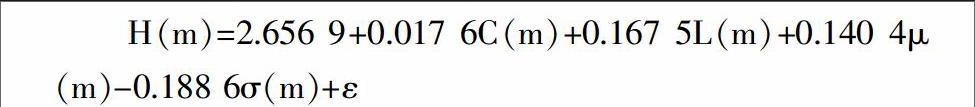
摘要：文章利用网络熵衡量银行系统稳定性，进而通过稳健主成分回归方法挖掘银行网络拓扑结构特征、股票收益率及其波动水平与银行系统稳定的内在关系。基于我国上市银行数据研究发现：网络聚集系数、平均最短路径以及平均收益率均与银行系统稳定性存在正相关关系；而平均波动率与银行系统稳定性存在负相关关系。

关键词：网络熵；银行系统；稳定性；稳健主成分回归

一、 引言

随着我国利率市场化进程逐步推进，将会导致银行利差缩窄，直接影响银行主要收入来源。即使在当前存款利率尚未完全放开的情况下，“余额宝”、“P2P借贷”、“众筹”等互联网金融创新已经对银行的存贷款利率造成巨大压力。其次，国家的隐性保护增强了我国商业银行的逆向选择和道德风险激励，而此致使银行的稳健性比较差。我国推出的存款保险制度，使得银行失去政府的隐性担保。在上述的背景下，我国银行系统的稳定性面临着严重的考验。而银行系统是现代金融系统的重要组成部分，保持银行系统的稳定是维护金融系统稳定的关键。因此，研究银行系统稳定的影响因素具有重要的意义。

目前学者们从不同的角度研究了不同的因素对银行系统稳定的影响，主要有：特许权价值、资产价格波动、影子银行、存款保险和利率市场化等。如唐建伟分析了资产价格波动主要通过信货风险渠道、市场风险渠道、经纪业务收入渠道、为附属机构注资的风险渠道及“第二回合” 渠道等传导渠道，影响到银行系统的稳定；Pais和Stork基于极值理论构造出指标研究了澳大利亚房地产行业价格波动对银行系统稳定性的影响王擎和白雪从理论和实证两个层面分析影子银行对银行体系稳定性的影响，并且考察了我国影子银行的总体承受能力以及各地区承受能力的差异。

银行系统总是不可避免地面临着各种风险的冲击，特别是来自资本市场的冲击。而目前基于银行资本市场数据研究的较多的是运用风险价值、条件风险价值或边际预期损失等技术研究银行系统性风险溢出效应，或者结合资产负债表对银行系统的风险传染以及系统重要性银行进行鉴别。对于上市银行而言，它们股票之间的价格波动关联使得银行间形成了一个复杂网络。该网络的节点表示银行，节点间的边表示银行股票之间的价格波动关联。而系统网络结构往往决定着系统功能，因此可以利用网络理论的技术与方法来研究银行系统稳定性。因此，本文以我国16家上市银行为研究对象，采用滑动时间窗口取样方法，构建银行动态网络，进而基于网络熵指标衡量银行系统稳定性。在此基础上，采用稳健主成分回归方法研究银行网络拓扑结构特征、股票收益率及其波动水平与银行系统稳定的内在关系。本文的创新之处在于：基于资本市场数据，从网络理论新的视角，研究了銀行网络结构特征和银行股票市场状态对银行系统稳定的影响，以期为银行风险管理和维护银行系统稳定提供决策依据。

二、 模型与方法

在本文中，我们采用股票收益相关性构建银行动态网络。假设有N家银行，Pi（t）表示银行i的股票在第t日的收盘价，则银行i的股票在第t日的对数收益率为：

Yi（t）=lnPi（t）-lnPi（t-1）（1）

进而可以得到银行i和银行j的股票收益率间相关性及其距离，分别如式（2）和式（3）所示：

根据股票间距离我们可以得到银行加权网络，其中股票间距离表示网络边的权重。但为了与传统的加权网络表示一致，即边的权重越大意味着银行股票间的价格波动一致性越强。因此，根据Peron等的研究，我们将股票间的距离dij转换为：

三、 实证分析

1. 数据来源。本文选取中国16家上市银行为研究对象，16家上市银行具体为交通银行、浦发银行、中国银行、华夏银行、建设银行、民生银行、招商银行、南京银行、工商银行、兴业银行、北京银行、光大银行、农业银行、中信银行、平安银行、宁波银行。研究的期限从2010年8月18日至2016年7月22日，所有银行股票的日收盘价数据经复权处理。在构建银行动态网络时，单个网络所使用的收益率序列时间长度τ=28，相邻两个银行网络的采样时间间隔δ=28，这使得构建网络数据不重叠。

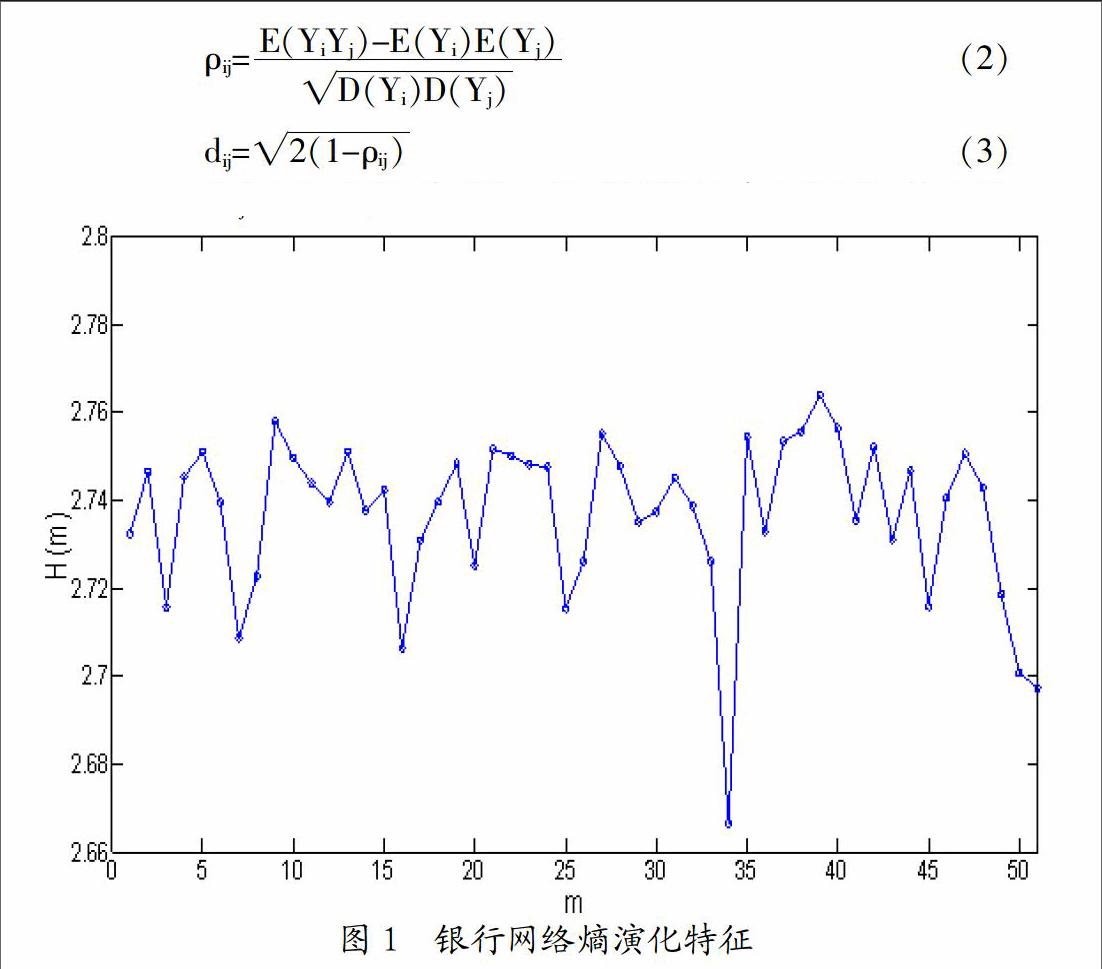
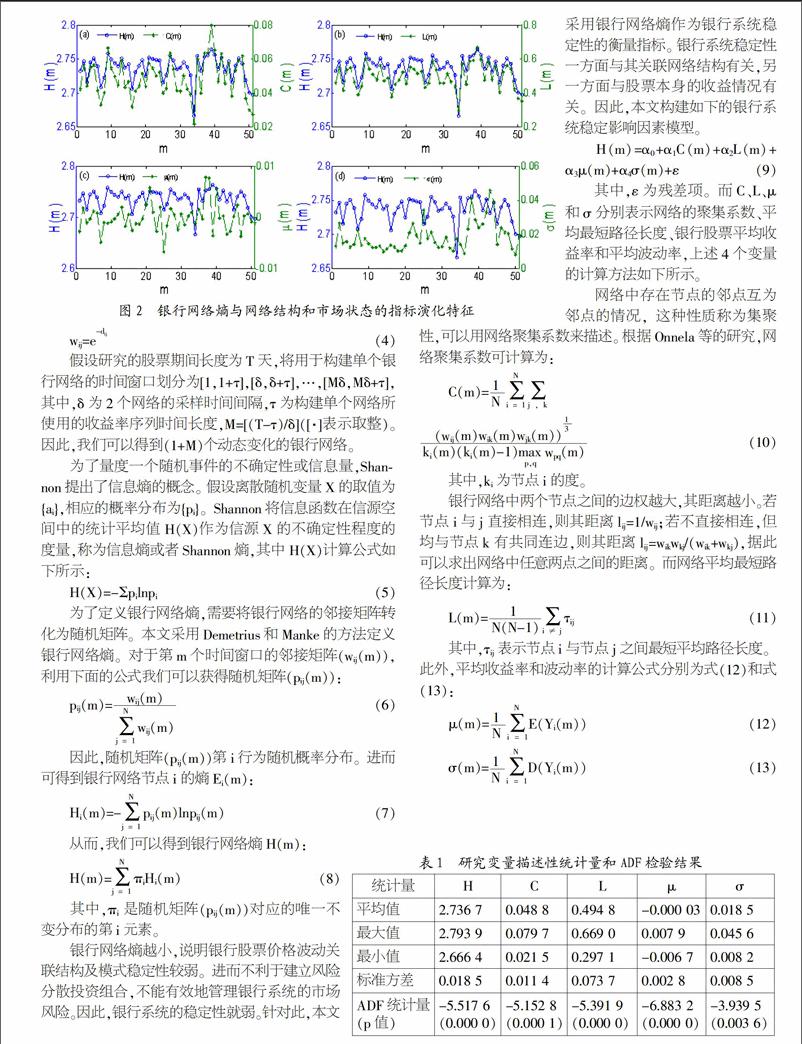
2. 银行网络熵、网络结构与市场状态演化特征。基于上述样本数据，根据公式（8）可以计算出银行网络熵结果，具体如图1所示。从图1可以看出除m=34外，银行网络熵处于小幅波动状态。而在m=34时银行网络熵最小，这意味着银行系统稳定性较差。这与银行行业指数变化是吻合的，因为m=34对应的时间段为2014年6月17日到2014年7月24日，在此期间银行行业指数801 780.SL变化波动较大，从2 103.38降到1 978.6，再反弹到2 062.84。下面我们先初步分析银行网络熵与银行网络聚集系数、最短平均路径长度、平均收益率和波动率之间关系，如图2所示。图2（a）-（d）分别同时揭示了银行网络熵与聚集系数、最短平均路径长度、平均收益率和波动率的时间演化特征。由图2可知，银行网络熵随时间演化规律基本上与聚集系数、平均路径长度和平均收益率相似，而在小部分情况下与平均波动率相反。

3. 影响因素回归结果。银行网络熵与聚集系数、最短平均路径长度、平均收益率和波动率究竟具有什么样关系呢？针对此，我们进一步进行计量模型检验。表1给出研究变量的描述性统计量和ADF单位根检验结果，从ADF检验结果可以看出：方程（9）中的5个变量均是平稳的。进而对自变量进行多重共线性检验，其方差膨胀因子（VIF）分别为 36.337、35.349、1.201、1.258，说明自变量之间存在多重共线性。此外，通过标准化残差可知存在异常值。针对此，本文使用Hubert 和Verboven提出的稳健主成分回归方法对方程（9）进行估计，该方法可以有效地处理多重共线性和异常值问题。Hubert 和Verboven不仅提出此方法，还提供了相应的Matlab 程序。基于Matlab软件，可以得到方程（9）的估计结果为：endprint

由上述估计结果可知，网络聚集系数、平均最短路径以及平均收益率均与银行系统稳定性存在正相关关系。这意味着网络聚集系数越大、平均最短路径越长以及平均收益率越高，网络熵值越大，银行系统稳定性越强。而平均波动率与银行系统稳定性存在负相关关系，这说明银行股票市场平均波动率越大，网络熵值越小，不利于银行系统稳定。

四、 结论

本文采用中国16家上市银行的收益率数据构建了一个动态银行网络，并建立回归模型分析了银行系统稳定性与网络结构和银行市场动态的关系。本文运用网络熵指标衡量银行系统的稳定性，并用网络聚集系数和平均最短路径来表示银行网络拓扑结构，用平均收益率和波动率来代表银行市场动态。通过稳健主成分回归方法估计的结果表明：网络聚集系数、平均最短路径以及平均收益率均与银行系统稳定性存在正相关关系；而平均波动率与银行系统稳定性存在负相关关系。本文的研究结果将有助于深入理解银行股票价格波动关联结构及模式稳定性，进而有利于银行风险管理，维护银行系统稳定。

参考文献：

[1] 唐建伟，李明扬，史智宇.资产价格波动与银行系统稳定[J].财贸经济，2006，（12）：3-10.

[2] Pais A， Stork P A.Contagion risk in the Australian banking and property sectors[J].Journal of Banking & Finance，2011，35（3）：681-697.

[3] 王擎，白雪.我国影子银行发展与银行体系稳定——来自省际面板数据的证据[J].财经科学，2016，（4）： 1-12.

[4] 钱水土，陈鑫云.国外银行系统性风险研究综述[J].经济理论与经济管理，2014，（34）：58-71.

[5] Peron T K D M， da Fontoura Costa L， Rodrigues F A.The structure and resilience of financial market networks[J].Chaos： An Interdisciplinary Journal of Nonlinear Science，2012，22（1）：013117.

[6] Shannon C E.A note on the concept of entropy[J].Bell System Technical Journal， 1948，27（3）：379-423.

[7] Demetrius L， Manke T.Robustness and network evolution-an entropic principle[J]. Physica A： Statistical Mechanics and its Applications，2005，346（3）：682-696.

[8] Lee D.Entropy of Global Financial Linkages[R].Bank of Korea WP2014-30，2014.

[9] Onnela J P， Saram？ki J， Kertész J， et al.Intensity and coherence of motifs in weighted complex networks[J].Physical Review E，2005，71（6）：065103.

[10] Hubert M， Verboven S.A robust PCR method for high-dimensional regressors[J].Journal of Chemometrics，2003，17（8-9）：438-452.

基金項目：国家自然科学基金项目“基于耦合网络的”企业—银行“系统性风险的传播机制及控制策略研究”（项目号：71573051）。

作者简介：李智（1970-），男，汉族，江苏省南京市人，南京大学理学博士，复旦大学应用经济学博士后研究员，研究方向为金融网络与金融风险管理；牛晓健（1971-），男，汉族，新疆维吾尔自治区阿克苏地区人，复旦大学经济学院教授、博士生导师，研究方向为金融风险管理。

收稿日期：2017-11-16。endprint