混凝土材料微裂纹模型研究

严 岿

(福建璟榕工程建设发展有限公司，福建 福州 350000)

1 概述

在对界面结合情况的分析中,需要得到添加纤维的软硬度与混凝土基体材料的关系,而实际上添加材料的长短与混凝土的强度也有着很大的关系,在实际应用中,我们通常采用了短纤维,纤维与混凝土结合处分布着很多的微裂纹,使得材料的增强效应降低。为此，如何研究混凝土材料微裂纹[1-4]，得到其结合特性就显得特别重要[5]。

2 模型的建立与分析

混凝土的主要功能为受压作用，对界面直裂纹进行研究具有重要的意义。混凝土材料对于界面处的微裂纹而言，相当于无限大体，于是可以采用无限平面结合材料界面裂纹进行分析。England对图1a)采用Goursat应力函数对其进行了解答，得到了理论解答。根据叠加原理，该理论解也可以用于图1b),于是得到了混凝土中纤维长度方向的裂纹受拉压解答，具体如下。

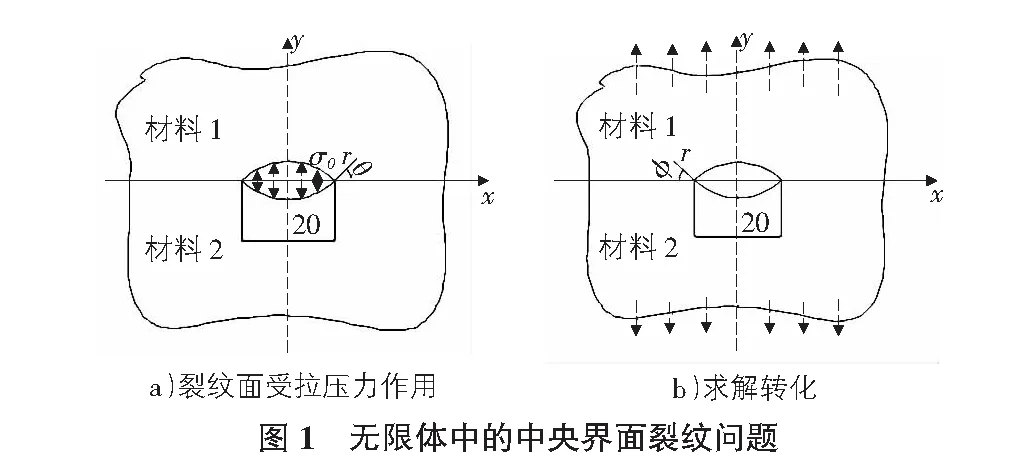
对于无限平面结合材料界面，England采用Goursat公式得到了如下解：

右裂尖：

左裂尖：

微裂纹对于混凝土材料而言，是很微小的，r≪a。

于是，右裂尖：

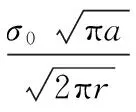
(1)

左裂尖：

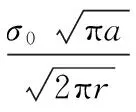
(2)

把应力强度因子定义为：

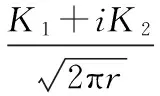
对于混凝土中中央界面裂纹受拉远场应力强度因子有：

右裂尖：

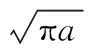
左裂尖：

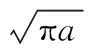
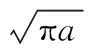
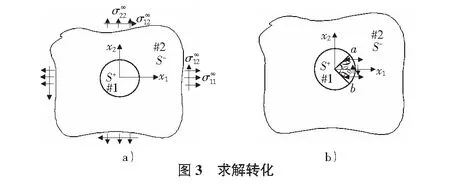
而混凝土中的纤维与混凝土基体结合面最主要的裂纹是环向裂纹，混凝土中常常受到较复杂的应力，如图2所示。对于此问题的解答，根据自洽定理，该问题可以分解为以下两个部分解答(图3a)+图3b))。

在平面问题下，根据复势理论，应力可以由以下方程表示：

(3)

(4)

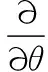
对于坐标变换有：

z=z0+z*eiδ；

φ*(z*)=φ(z)；

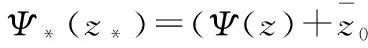
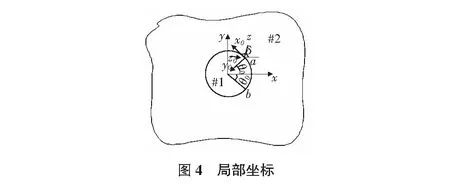
对于图3a)，图3b),文献根据坐标变换(见图4)，引入复变函数，分别给予了解答。

于是得到了复杂应力条件下的强度因子：

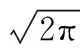
(6)

其中,Λ=[(α+β)/(1-β)];

Π=[(α-β)/(1+β)]；

X0(z)=(z-a)1/2+iε(z-a)-1/2-iε。

此时，界面上的应力奇异性要复杂得多，不仅仅与材料的参数α,β有关，也与夹角θ0有关，但是研究材料的结合性能可以给定一个夹角θ0,然后讨论参数α,β对结合性能的影响。

3 结语

混凝土的主要功能为受压作用，对界面直裂纹进行研究具有重要的意义，本文通过微观模型的建立，研究了纤维与混凝土基体材料的结合性能，这将对研究纤维材料对混凝土的增强有重要的理论价值。

[1] 吴佰建,李兆霞,郭 力,等.模拟混凝土破坏过程的微裂纹模型及其应用[J].东南大学学报(自然科学版),2013(5):1034-1038.

[2] 吴佰建.脆性微裂纹材料及构件的损伤跨尺度演化分析理论与计算方法[D].南京：东南大学,2015.

[3] 齐 辉,李范春,周健生,等.考虑初始等距共线微裂纹列影响的Ⅲ型裂纹体的蠕变断裂分析[J].哈尔滨工程大学学报,2001,22(1):87-91.

[4] 张德海,朱浮声,邢纪波,等.混凝土拉伸断裂的细观数值分析[J].计算力学学报,2006,23(1):65-70.

[5] 赵爱红,虞吉林.准脆性材料的细观损伤演化模型[J].清华大学学报(自然科学版),2000,40(5):88-91.