基于压缩感知的心电信号采集电路实现

江浩+钱慧+徐明月+王仁平

摘 要：心电采集系统普遍存在数据量大、功耗大的问题。为解决这个问题，文中引入了基于压缩感知的随机解调采集方案，设计了随机解调的具体电路，以实现心电信号压缩采样。对于奈奎斯特率为360 Hz的心电信号，采样率仅为60 Hz，同时采集到的信息量比传统采样电路低很多，由此达到了降低数据量和实现低功耗的要求。

关键词：压缩感知；随机解调；压缩采样；心电信号

中图分类号：TP391.41；TN432 文献标识码：A 文章编号：2095-1302（2017）12-00-04

0 引 言

随着现代信息技术的发展，便携式智能终端成为医疗仪器设备发展的趋势[1，2]。便携式心电监护系统由于其实时性、可24小时不间断监护等特点而被广泛应用。现有的便携式心电监护终端一般先实时采集用户的心电信号，然后通过无线传输模块远程传输给监护中心，在监护中心对用户的心电信号进行分析和处理。为满足有效分析的需要，现有的便携式心电采集设备一般采用250 Hz及以上采样率，12位量化位宽的ADC采集信号。这样的采集方式导致现有的便携式心电采集系统普遍数据量较大。文献[3]的研究表明，现有心电采集系统功耗的30%用于数据传输。显然，对于便携式心电采集设备，降低数据传输速率可以有效降低功耗[4-6]。

压缩感知（Compressive Sensing，CS）理论是近年来信号处理领域诞生的一种新的信号处理理论[7，8]，由D. Donoho （美国科学院院士）、E. Candes（Ridgelet， Curvelet创始人）及华裔科学家T. Tao（2006年菲尔兹奖获得者）等人提出。文献[9]首次将压缩感知应用到心电信号采集中，通过实验证明采用压缩感知可以有效压缩并重构心电信号，证明了压缩感知在心电信号采集系统应用的可行性。目前，国内高校和研究机构也在这方面展开了研究。但这些方法都是采用先采样后压缩的方式，在离散时间域处理心电信号，并未真正降低心电采集系统的复杂性。

本文拟根据压缩感知的基本原理，利用模拟信息转化采样结构在连续时间域实时采集心电信号。相对于现有的压缩感知心电信号采集方法，本文在采集信号过程中压缩信号，可以有效降低系统功耗。文中设计了前端R波信号检测的压缩采样具体电路。用MIT-BIH心电数据库的信号作为仿真源，进行系统级和电路级的仿真。通过正交匹配追踪算法和基于小波变换的R波检测算法完成对信号的重构。

1 模拟信息转换系统基本原理

模拟信号转换是一种连续时间域的压缩感知方法。2006年Sami Kirolos， Jason Laska等人根据压缩感知原理，通过随机解调模块和積分器构建了可实现的观测矩阵，从而将离散时间压缩感知推广到连续时间域。因此，模拟信号转换系统又称为随机解调（Random Demodulator， RD）[10-12]。

1.1 系统架构

随机解调系统如图1所示，主要包括解调、积分和均匀采样三部分。首先将输入信号f（t）与伪随机序列p（t）相乘（解调），对输入信号进行离散化处理，然后通过积分电路压缩信号，再由采样率低于奈奎斯特率的ADC对信号进行采样，获得一系列观测数据y[m]。

输入信号f（t）是一个包含K个整数频率分量的谐波信号，最高频率不高于W/2，可以表示为：

其中，Ω是一组K个整数频率集合，它满足Ω{0，±1，±2，…，±（W/2-1），±W/2}。式（1）中aω为幅值，有K个不为零的值。根据奈奎斯特采样定理，如果对输入信号f（t）进行采样，其采样频率应大于等于奈奎斯特率W。然而输入信号只有K个有效频率点，其值远远小于W。根据信号模型式 （1），其携带的信息量只有R=O（Klog（W/K））比特。因此，只要获得R比特的信息量，就可以重构原始信号[13]。

1.2 数学模型

在理想状况下，RD系统是一个线性系统，它将连续时间域的信号映射到一系列离散值。为了便于理解，我们将这个过程用矩阵模型表示。根据压缩感知的基本原理，随机解调的积分处理是一个求和的过程，可以应用均值思想将信号描述为离散时间形式，如式（2）：

伪随机序列与输入信号相乘，则伪随机序列可表示为式（4）所示的W×W矩阵：

假设积分时间为Ts，设系统采样率为N，每一次积分电路采集的值为W/N个信号的xn累加和。如此，积分采样过程可以用K×W矩阵H表示，如式（5）所示：

可见A=HD就是信号X的感知矩阵，即压缩感知理论中的ACS。信号经过压缩观测后，最终得到信号X的压缩观测值为：

观测值通过正交匹配追踪算法和基于小波变换的R波检测算法可以重构信号。

2 模拟信息转换电路

根据模拟信息转换采集系统，设计前端电路，并进行仿真验证。

2.1 采样系统设计

2.1.1 随机解调电路设计

解调电路采用开关混频来实现，其电路如图2所示。

为了增强电路的抗干扰能力，采用全差分结构。开关S1（包括S1a和S1b）由随机序列φm控制。φm是以周期Tc=1/W时钟作为基准产生数字形式的PN序列：

φ（t）是持续时间为Tc的基带脉冲波形，也是积分器开关的控制信号，εn值以一定概率在0和1之间变化。控制信号φR（t）为持续时间为NTc的基带脉冲波形，作为积分器的重置信号。对于间隔NTc～（N+1）Tc，当PN序列φm为高电平时，开关S1a闭合，S1b断开，则混频器输出的电压为：

反之，当φm为低电平时，开关S1a断开，S1b闭合，则混频器输出的电压为：

Vm+（t），Vm-（t）为积分电路的输入。

2.1.2 积分模块设计endprint

積分电路如图3所示，采用差分结构标准的开关电容积分电路，开关由两相不交叠的时钟φ和控制。该电路有三个工作阶段，分别为重置阶段、采样阶段和积分阶段。

假设系统的压缩采样时间间隔为Ts=NTc。重置阶段，φR为高电平时，开关SW5，SW6闭合，放大器的输入和输出短路，输出电压VoD（t）=Vo+（t）-Vo-（t）近似等于零。当t=nTc时，φ为高电平，进入采样阶段，开关SW1，SW3闭合，SW2，SW4断开，输入信号对电容Cs充电，充电电压为Vm+（t）-Vcm（t）。当t=nTc+Tc/2时，采样完成， Cs中的电荷量为Q1，如式（10）：

此时，由于SW4处于断开状态，使得Cs与后面的积分电路断开，放大器的输出仍保持为零。当t=nTc+Tc/2时，进入积分阶段，控制信号变为高电平，开关SW2，SW4闭合SW1，SW3断开，此时电容Cs将在前Tc/2积攒的电荷Q1全部转移到中Cf，极性相反，并与电容原有的电荷进行叠加，得到系统在t=（n+1）Tc时刻的输出VoD（（n+1）Tc）。此时根据电荷转移的关系得到式（11）：

由于Ts=NTc，电荷累积转移过程将被执行N次，可以得到积分电路差分输出两端的电压值，分别如式（12）和式（13）所示。输出电压差分值见式（14）。至此，一次积分完成时对输出信号进行采样，可获得观测向量中的一个值。此过程不断重复，最终得到观测向量y。

2.2 设计验证分析

为了分析开关随机解调电路系统的基本特性，考虑将式（14）转换到s域，如式（16）所示：

显然，式（16）所示的系统传输函数与随机解调理论模型的系统函数一致。由此可见，本文所涉及的电路能很好地逼近原始随机解调理论设计模型。根据压缩感知的基本原理，在Matlab中绘出理想情况下的系统函数图，如图4所示。

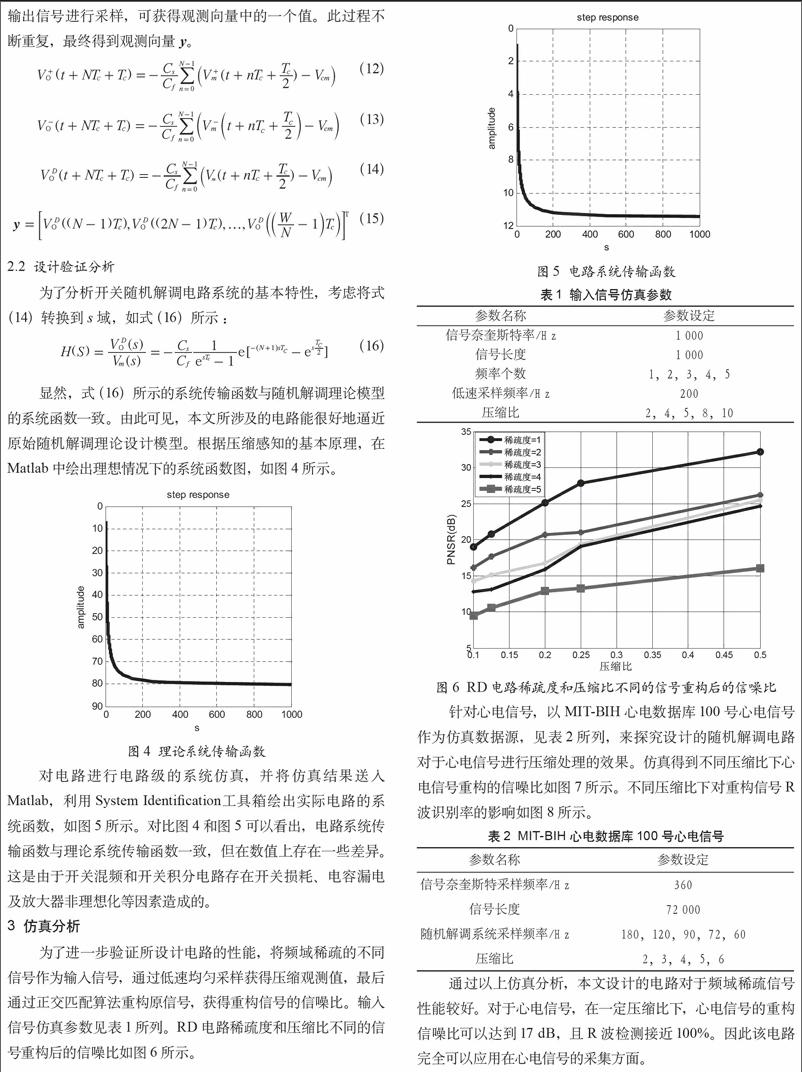
对电路进行电路级的系统仿真，并将仿真结果送入Matlab，利用System Identification工具箱绘出实际电路的系统函数，如图5所示。对比图4和图5可以看出，电路系统传输函数与理论系统传输函数一致，但在数值上存在一些差异。这是由于开关混频和开关积分电路存在开关损耗、电容漏电及放大器非理想化等因素造成的。

3 仿真分析

为了进一步验证所设计电路的性能，将频域稀疏的不同信号作为输入信号，通过低速均匀采样获得压缩观测值，最后通过正交匹配算法重构原信号，获得重构信号的信噪比。输入信号仿真参数见表1所列。RD电路稀疏度和压缩比不同的信号重构后的信噪比如图6所示。

针对心电信号，以MIT-BIH心电数据库100号心电信号作为仿真数据源，见表2所列，来探究设计的随机解调电路对于心电信号进行压缩处理的效果。仿真得到不同压缩比下心电信号重构的信噪比如图7所示。不同压缩比下对重构信号R波识别率的影响如图8所示。

通过以上仿真分析，本文设计的电路对于频域稀疏信号性能较好。对于心电信号，在一定压缩比下，心电信号的重构信噪比可以达到17 dB，且R波检测接近100%。因此该电路完全可以应用在心电信号的采集方面。

4 结 语

针对便携式心电监测设备数据压缩和低功耗设计的需求，文中提出一种基于压缩感知的心电采集方案，并设计了前端采集的具体电路。针对心电信号的稀疏性，对信号、RD系统建模，分析其系统特性。采用随机解调的方案实现心电信号压缩采样。仿真结果表明，对于奈奎斯特率为360 Hz的心电信号，其采样率仅为60 Hz，远低于奈奎斯特率。同时采集的信息量比传统采样电路也低得多。由仿真结果我们可以预知，所设计的采样电路得到的观测值很好重构，但设计的电路受开关损耗、电容漏电及放大器不理想因数的影响，使其与系统要求存在一定差距。后续可以从电路设计的方向寻找补偿方法来提高电路性能。

参考文献

[1]董康然.基于移动互联网技术的全科医生便携式智能诊疗系统的设计与开发[J].中国全科医学，2014，17（28）：3404-3406.

[2]孙荣贵，李丕丁，曾红雨，等.一种使用智能移动终端的便携式医用内窥镜图像显示方法[J].国际生物医学工程杂志，2017，40（1）：24-27.

[3]吕海洋，张鹏辉，邓建国，等.超低功耗无线传感心电信息监控系统设计[J].实验室研究与探索，2014，33（1）：110-114.

[4]屈信超，张跃.基于压缩感知的实时心电信号压缩算法[J]. 计算机工程与设计，2014（10）： 3450-3454.

[5]罗堪，李建清，王志刚，等.心电压缩感知恢复先验块稀疏贝叶斯学习算法[J].仪器仪表学报，2014（8）：1883-1889.

[6]寇鹏.心电信号压缩方法研究及其DSP系统实现[D].北京：北京工业大学，2004.

[7] Emmanuel J Candès， Justin Romberg，Terence Tao. Robust Uncertainty Principles：Exact Signal Reconstruction From Highly Incomplete Frequency Information [J].IEEE Transactions on Information Theory， 2006，52（2）：489-509.

[8] Donoho D L. Compressed sensing [J]. IEEE Transactions on Information Theory，2006，52（4）： 1289-1306.

[9] Fei H， Meng J， Wagner M， et al.Privacy-Preserving Telecardiology Sensor Networks： Toward a Low-Cost Portable Wireless Hardware/Software Codesign [J].IEEE Transactions on Information Technology in Biomedicine， 2007，11（6）：619-627.

[10] Kirolos S， Laska J， Wakin M， et al. Analog-to-information conversion via random demodulation[C].2006 IEEE Dallas/CAS Workshop on Design， Applications， Integration and Software，IEEE， 2006： 71-74.

[11] Saini Kirolos， Tamer Ragheb， Jason Laska，et al.Practical Issues in Implementing Analog-to-Information Converters [C].The 6th International Workshop on System on Chip for Real Time Applications：141-146

[12] Jason N Laska， Sami Kirolos， Marco F Duarte，et al.Theory and Implementation of an Analog-to-Information Converter using Random Demodulation[C].2007 IEEE International Symposium on Circuits and Systems： 1959-1962.

[13] Joel A Tropp， Jason N Laska， Marco F Duarte，et al.Beyond Nyquist： Efficient Sampling of Sparse Bandlimited Signals [J].IEEE Transactions on Information Theory， 2010，56（1）：520-544.endprint