窄缝消能工冲击波及水翅特性研究
2018-01-10,,,,
, ,,,
(长江科学院 水力学研究所,武汉 430010)
窄缝消能工冲击波及水翅特性研究
胡晗,杨伟,黄国兵,侯冬梅,杜兰
(长江科学院 水力学研究所,武汉 430010)
窄缝消能工(STED)是一种结构简单、消能高效率的消能设施,广泛应用于高水头、大流量及窄河谷条件的水利工程。然而,由收缩段中冲击波造成的水翅作为窄缝消能工的一种特殊水力现象,将给下游岸坡稳定性和建筑安全带来危害,而由水翅造成的危害没有引起足够的重视,因此有必要对冲击波的形成机制及由此造成的水翅的运动特性进行专门研究。通过模型试验深入研究流态,结合理论分析揭示了窄缝消能工冲击波和水翅之间的内在联系。通过加入修正系数的方式将Ippen理论应用于窄缝消能工中,提出了冲击波波角的简化计算公式和水翅影响范围的估算方法。模型试验的结果显示该估算方法能够精确反映水翅的影响范围,计算相对误差在5%以内。
窄缝消能工;水流冲击波;水翅;运动特性;模型试验
1 研究背景
窄缝消能工采用了特定的挑坎收缩体型,当水流通过收缩段时沿横向收缩,沿纵向伸展[1-2]。在此过程中,水流中的能量被大量耗散,从而有效减轻了水流对下游河槽的冲刷和侵蚀[3-4]。正是由于窄缝消能工消能效率高的优势,其被广泛应用于高水头、大流量及窄河谷条件的水利工程中,成功解决了包括龙羊峡水电站、二滩水电站、水布垭水电站[5]以及隔河岩水电站等多个大型水利工程中的消能难题。
多位研究者通过理论推导和试验方法,从能量耗散效率、结构安全、水面特征、压力和空化特征、水舌形态、下游河床的冲刷效应等方面研究了窄缝消能工。张彦法等[6]、戴震霖等[7]研究了窄缝水舌的运动扩散规律,给出了窄缝收缩段水面线和水舌挑距的估算公式。吴建华等[8]提出了计算水舌形态的经验公式,并通过模型试验研究了水流的壅塞效应[9]。柳杨等[10-11]对窄缝反弧收缩段动水压强的计算方法进行了探讨。
由收缩段冲击波造成的水翅作为一种特殊的水力现象,将给下游岸坡稳定性和建筑安全带来危害。然而,由水翅造成的危害没有引起足够的重视。因此,有必要对冲击波的形成机制及由此造成的水翅的运动特性进行专门研究。本文通过模型试验和理论分析,揭示了冲击波和水翅运动特性的内在联系。
2 试验装置和方法
水工模型及试验装置示意如图1所示,采用高水箱模拟上游水库,主体建筑物采用有机玻璃制作。试验中采用高速摄影技术捕捉冲击波形态、碰撞水翅形态及其运动轨迹;采用水滴粒子采集分析仪对水翅体量的空间分布进行分区定量观测。倾斜水槽尺寸为长3.2 m、宽0.2 m,在靠近窄缝消能体型收缩段入口处安装一个弧形闸门,用来调节进入收缩段水流的弗劳德数,模型材质为有机玻璃。
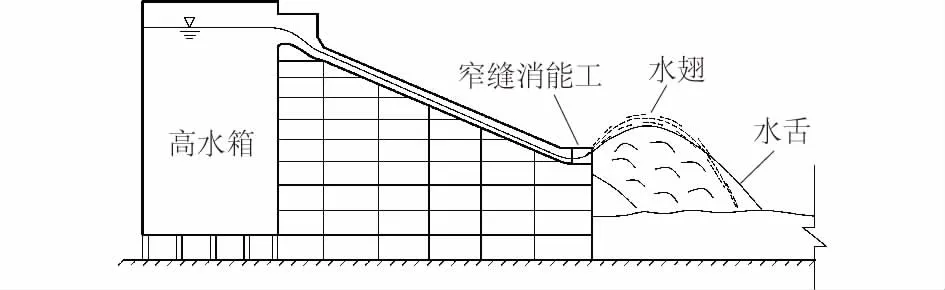
图1 水工模型及试验装置示意图Fig.1 Hydraulic model and experimental settings
窄缝消能工的主要几何参数:收缩段的长度L,挑角α,收缩段入口宽度B和出口宽度b,于是收缩比为b/B。
本研究总共设置了9个体型,采用不同的收缩比(b/B=0.20,0.25,0.30)和不同的挑角(α=0°,5°,10°),窄缝消能工收缩段长度为0.5 m。模型的几何特征如表1所示。模型试验系统地采用了不同弗劳德数(4.10~5.95)的进口水流,流量保持为0.1 m3/s。
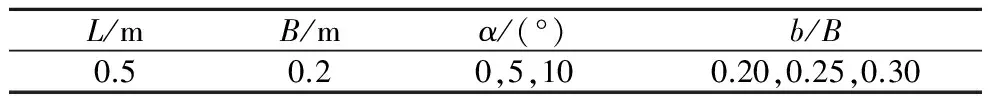
表1 窄缝消能工模型的几何特征Table 1 Geometric parameters of slit-type energydissipator model
3 流态观察
3.1 收缩段内的流态
如图2所示,在收缩段上游,来流保持自由明渠流态、自由表面和静水压力分布。当水流通过窄缝消能工收缩段时沿横向收缩,沿纵向伸展。由于窄缝消能工边墙的收缩,下泄的高速水流对两侧边墙产生强烈的冲击,收缩段内水流产生了急流冲击波。在收缩段内,自由表面不再与坡面保持水平。

图2 收缩段流态Fig.2 Flow regimes in contracted section
收缩段内水流的水力特性受到2个因素的影响:侧壁糙率造成的摩擦影响和自由流区的大涡体紊动惯性作用。由于冲击波交汇点和收缩部分的入口之间的距离较短,侧壁糙率造成的摩擦影响可以忽略。另一方面,在收缩边墙附近,由于高速来流惯性力,产生了冲击波(一种特殊的水跃)。
在冲击波交汇后,水流的紊动不断加剧[12],一方面,由于边墙继续收缩,沿程水深加大,流速减小,水流的惯性作用相应减小,涡体尺寸受到两侧边墙的限制,较大的涡体不断破碎分裂成较小的涡体;另一方面,冲击波交汇后的水流对两侧边墙而言相对较平顺。水流中大小涡体并存,但起主导作用的仍是大涡体的紊动惯性作用。
当一定条件下的水流进入窄缝收缩段后,由于侧墙收缩作用,两侧水面沿程迅速升高,而中线水面沿程也增高,但雍高程度较边墙低,故边墙水面线比中线水面线要高,断面水面呈“U”型。当两侧冲击波相遇交汇之后,断面水面呈“W”型,两侧水面随着边墙进一步收缩而继续上升,而中间水面则急剧升高超过边墙水面线并脱离主体水流,具有较大的向斜上方的初速度,会以散射的方式抛射出去,此时的边墙水面线要低于中线水面线。这也就是水翅的成因。
3.2 水舌形态
图3展示了窄缝消能工的水舌形态,窄缝消能工的主体水舌由沿纵向伸展的主体水流形成。由于收缩段内冲击波的碰撞,部分水体脱离了主流水体以散射的方式抛射出去,这就是水翅的主要来源。部分水翅直接汇入主体水舌落入下游,这部分水翅不会对下游岸坡和建筑物造成危害;另外一部分水翅向下游散射,落到主体水舌的两边,引起了对下游特定区域岸坡和建筑物的持续冲刷降雨。因此,预测水翅的影响区域,并以此为参考对下游岸坡和建筑物进行有针对性的防护是至关重要的。

图3 水舌形态Fig.3 Nappe form
4 窄缝消能工冲击波计算
冲击波的形状是影响窄缝消能工运行的关键因素。Ippen[13]提出了基于静水压强假设的冲击波基本公式,即
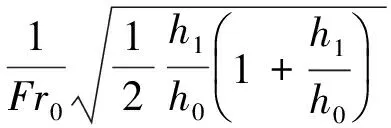
(1)
式中:β为冲击波波角;h0,h1分别为上下游水深;Fr0为来流的弗劳德数。
Hager等[14-15]和刘韩生等[16]对Ippen的公式进行了简化,根据Ippen提出的理论有以下两式:

(2)
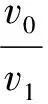
(3)
式中:φ为冲击波和收缩边墙之间的角度;v0,v1分别为冲击波上下游的流速。
于是,

(4)
比能不变假定可表达为
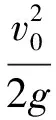
(5)
式中H为冲击波交汇前后断面的总水头。
将式(1)、式(4)、式(5)合并可得

(6)
对于微冲击波,令Δh=h2-h1,将式(6)进行泰勒级数展开、忽略高阶小量得
(7)
忽略一阶小量得φ的冲击波简化式为
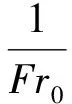
(8)
于是,φ可简化表达为
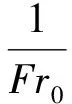
(9)
然而,窄缝坎边墙偏转角较大,冲击波后不再符合静水压力假定,直接用 Ippen理论研究窄缝挑坎中的冲击波误差较大,需要进行修正。
假设
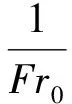
(10)
式中c为基于窄缝消能工几何参数和来流流态的修正系数。
假定修正系数c的影响因素包括:挑角α,边墙偏转角θ和来流弗劳德数Fr0。正交分析的结果显示只有边墙偏转角θ和来流弗劳德数Fr0对修正系数c产生了显著影响。
试验结果显示,以偏转角θ=10°,来流弗劳德数Fr0=5.3工况为例,修正系数c和挑角α之间的关系如图4(a)所示。当挑角α在0°,5°,10°之间变化时,修正系数c的变化幅度仅为1.2%,因此认为挑角α不会对修正系数c产生显著影响。图4(b)描述了不同边墙偏转角θ情况下,修正系数c和来流弗劳德数Fr0之间的关系。
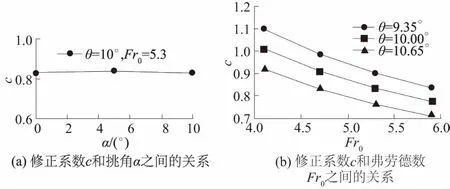
图4 修正系数c与挑角α和来流弗劳德数Fr0之间的关系Fig.4 Variation of correction coefficient c with bucket angle α and Froude number Fr0 of incoming flow
通过最小二乘法得出了修正系数c的经验计算公式,即
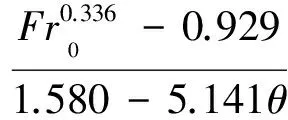
(11)
最后,得出了窄缝消能工冲击波波角的简化计算公式,即
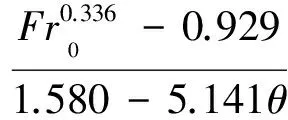
(12)
5 窄缝消能工水翅范围计算
窄缝挑坎的水翅现象是由于挑坎内2股急流冲击波交汇碰撞后,部分水体提前挑射并脱离主体水舌向下游及周围裂散而成。水翅裂散后一部分跌落与主体水舌混掺,另一部分则向周围抛洒,形成非天然超强降雨。若泄水建筑物临岸布置,则这部分超强降雨水体将对岸坡造成有力冲击,对其稳定性构成威胁,将此部分水体定义为次生水翅,也是本文重点研究的对象。
如图5所示建立坐标系。坐标原点O位于收缩段起始处中心,距离底板高度为z。冲击波碰撞于C点。水翅以最大的出射角γ并跟随边墙附近的两股水流从主体水舌两侧跌落,落点为D。于是LCD定义为落点D与冲击波交汇点C的水平距离;LM为落点D与原点的纵向距离;TM定义为落点D与中心线的横向距离。于是,水翅的影响范围可以用LM和TM来概括。

图5 冲击波与水翅示意图Fig.5 Schematic diagram of shock wave and water wing
则由几何关系可得:
TM=LCDtanβ,
(13)
LM=LOC+LCD,
(14)

(15)
忽略空气阻力,把挑射水流的运动看作质点的自由抛射体运动,LCD可近似按自由抛射体的运动轨迹来计算。根据自由抛射体运动原理可以求得

(16)
式中:vC,γ,hC分别为冲击波交汇点C处的流速、出射角度和水深;g为重力加速度。因此,确定了vC,γ,hC后,可得到LCD的值。
Ippen 冲击波理论给出了冲击波波后水流流速,即

(17)
式中v0为冲击波交汇点上游的流速。
根据连续性方程(式(18))可得冲击波交汇点C处的水深hC。
v0h0B=vChCBC。
(18)
式中BC为冲击波交汇点C处的断面宽度。
于是,

(19)
试验结果(图6)表明,窄缝坎中线截面上的水面线,可用抛物线函数来近似表达,即
y=px2+h0。
(20)
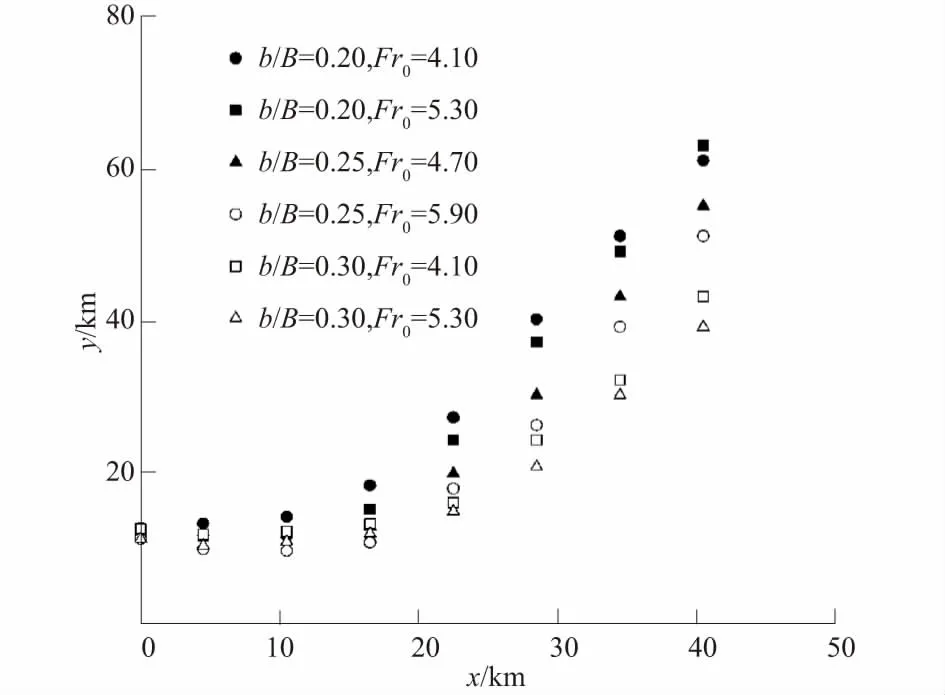
图6 不同工况下窄缝坎中线截面上的水面线Fig.6 Flow surface along the central line of slit bucket in various working conditions
根据前文定义,冲击波交汇点C的坐标为(LOC,hC),因此

(21)
将式(21)代入式(20),抛物线函数表达式为

(22)
在C点(LOC,hC)对式(22)求导,可得冲击波交汇点(LOC,hC)处水流的出射角度,即
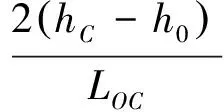
(23)
因此
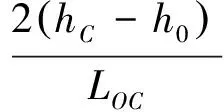
(24)

图7 不同体型和工况下计算水翅范围和试验水翅影响区域的对比Fig.7 Comparison of water wing area between experiment result and calculated result for different bucket types under various working conditions
为了验证式(13)和式(14)的精度,将计算得到的LM,TM和试验得到的水翅降雨影响区域进行对比,如图7所示。
由于难以确定水翅降雨区域的边界,确定降雨强度500 mm/h等值线以内的区域为典型水翅影响区域。
根据图7的比较验证,不同体型和工况下的典型水翅影响区域恰好被由式(13)和式(14)计算得到的估算范围LM,TM所包围。LM的最大估算误差和平均估算误差分别为4.4%和3.0%;TM的最大估算误差和平均估算误差分别为4.7%和2.6%。因此该方法能准确估算水翅的典型影响范围。
6 结 论
通过模型试验深入研究流态,结合理论分析揭示了窄缝消能工冲击波和水翅之间的内在联系。通过加入修正系数,将Ippen理论应用于窄缝消能工中,提出了冲击波波角的简化计算公式和水翅影响范围的估算方法。模型试验的结果显示该估算方法能够精确反映水翅的影响范围,计算相对误差在5%以内。
[1] CHENG Chun-tian,SHEN Jian-jian,WU Xin-yu,etal. Operation Challenges for Fast-growing China’s Hydropower Systems and Respondence to Energy Saving and Emission Reduction[J]. Renewable and Sustainable Energy Reviews,2012,16(5): 2386-2393.
[2] 李乃稳,许唯临,周茂林,等.高拱坝坝身表孔和深孔水流无碰撞泄洪消能试验研究[J].水利学报,2008,39(8):927-933.
[3] 肖兴斌.窄缝式消能工在高坝消能中的应用与发展综述[J].水电站设计,2004,20(3):76-81.
[4] 陈忠儒,陈义东,黄国兵.窄缝式挑坎体型研究及其挑流水舌距离的估算[J].长江科学院院报,2002,19(4):11-14.
[5] 马吉明,张永良,郑双凌.水布垭工程差动窄缝挑坎型溢洪道水力特性的试验研究[J].水力发电学报,2007,26(3):93-98.
[6] 张彦法,吴文平.窄缝挑坎水面线及水舌挑距的试验研究[J].水利学报,1989,(5):14-21.
[7] 戴震霖,于月增.深孔窄缝挑流水力参数及挑距的研究[J].陕西水力发电,1992,8(1):7-13.
[8] WU Jian-hua,MA Fei,YAO Li. Hydraulic Characteristics of Slit-type Energy Dissipaters[J]. Journal of Hydrodynamics,2012,24(6): 883-887.
[9] WU Jian-hua, WAN Bin, MA Fei,etal. Flow Choking Characteristics of Slit-type Energy Dissipaters[J]. Journal of Hydrodynamics,2015,27 (1):159-162.
[10] 柳 杨,马 飞,吴建华.窄缝坎的冲击波及水舌入水宽度的计算[J].水利水电科技进展, 2014,34(3):20-23.
[11] 黄智敏,何小惠,朱红华,等.窄缝式挑坎体型及动水压强特性分析[J].中国农村水利水电,2006,(5):69-71,74.
[12] LUO Bei-er,WANG Jun-xing,ZHANG Ying-ying. Researches on the Chaotic Characteristics of Fluctuating Pressure in Slit-type Energy Dissipator[J]. Advanced Materials Research,2014,1025/1026: 1150-1159.
[13] IPPEN A T. Gas-wave Analogies in Open Channel Flow[C]∥University of Iowa.Proceedings of the 2nd Hydraulics Conference. Iowa, June 1-4, 1942:248-265.
[14] HAGER W H,BRETZ N V.Discussion of “Simplified Design of Contractions in Supercritical Flow” by Terry W. Strum[J].Journal of Hydraulic Engineering,1987, 113(3): 422-427.
[15]HAGER W H, SCHWALT M, JIMENEZ O,etal. Supercritical Flow near an Abrupt Wall Deflection[J]. Journal of Hydraulic Research, 1994,32(1):103-118.
[16]刘韩生,倪汉根.急流冲击波简化式[J].水利学报,1999,21(6):56-60.
Characteristics of Shock Waves and Water Wing inSlit-type Energy Dissipators
HU Han,YANG Wei,HUANG Guo-bing,HOU Dong-mei,DU Lan
(Hydraulics Department, Yangtze River Scientific Research Institute, Wuhan 430010, China)
Slit-type energy dissipator is widely used in hydraulic projects of high water head, large discharge, and narrow river valley due to its simple structure and high efficiency. The water wing caused by shock waves in the contracted section of slit-type energy dissipator may bring about harmful effects, which, however, has not
sufficient attention. In this article, the hydraulic characteristics of slit-type energy dissipator are investigated by means of physical model and theoretical analysis to reveal the internal relation between shock waves and water wings. A correction coefficient is introduced for the application of Ippen’s theory to slit-type energy dissipator. The expression of the coefficient is obtained, and simplified formulas for shock wave angle and water wing scope are theoretically derived, which was verified accurate by experimental data, with the relative error within 5%.
slit-type energy dissipator; shock wave of flow; water wing; motion characteristics; hydraulic modelling
2016-09-10;
2016-10-25
国家自然科学基金项目(51709014);国家重点研发计划项目(2016YFC0401904);中央级公益性科研院所基本科研业务费专项(CKSF2017055/SL,CKSF2017011/SL)
胡 晗(1988-),男,湖北武汉人,工程师,博士,主要从事枢纽与电站水力学方面的研究。E-mail:smith_hu@qq.com
10.11988/ckyyb.20160972
TV321
A
1001-5485(2018)01-0086-05
(编辑:罗 娟)
