Ka波段波导H面膜片滤波器的分析与计算

王标

摘 要：采用模式匹配法对Ka波段波导H面膜片滤波器的不连续性进行了分析，并利用Matlab编程对滤波器的S11和S21参数进行计算。得出波导滤波器的3dB带宽约为32.6～34.5GHz，并对算法和滤波器的设计问题做了进一步的讨论。

关键词：波导滤波器 H面膜片 模式匹配 散射參数

中图分类号：TN713 文献标识码：A 文章编号：1672-3791（2017）11（b）-0240-04

模式匹配法是求解电磁场边值问题最直接的方法，它简单明了，物理概念清晰；计算简单，计算时间短，内存需求少；有解析表达式，运算方便；理论上讲，两边的模式数趋于无穷时，可得到严格解[1]。它比较适用于求解波导等微波器件的不连续性问题。通过网络综合，可以分析、设计和优化波导T接头，多模喇叭，功分器，皱纹波导滤波器，波导移相器等微波元器件和微波子系统。

本文采用模式匹配法对波导滤波器的不连续性进行分析，并利用Matlab编程对波导滤波器的S11，S21参数进行仿真。

1 问题阐述

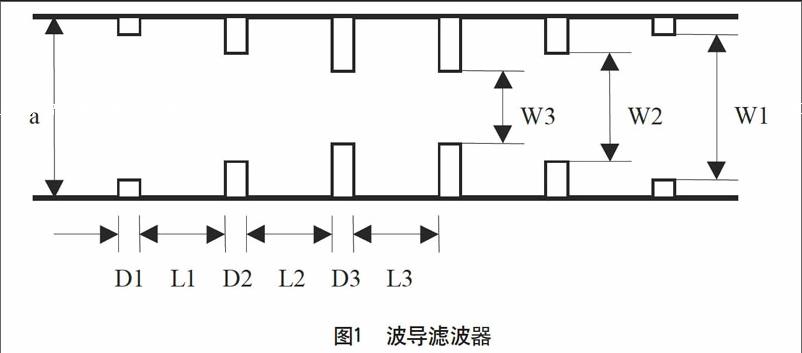
Ka波段波导H面膜片滤波器的结构如图1所示，结构参数为：a=7.12mm，b=3.56mm，D1=D2=D3=1.20mm，L1=4.20mm，L2=4.83mm，L3=4.90mm，W1=3.90mm，W2=2.85mm，W3=2.65mm，利用模式匹配法，在30～38G频率范围内分析波导滤波器的S11，S21参数。

2 理论分析

如图1所示，该波导滤波器由若干个微波不连续结构构成，可以分解成若干个膜片，每个膜片又有两个对称的H面阶梯和一段传输线构成。因此用模式匹配法分析该波导滤波器的基本思想是，利用模式匹配分析计算每个膜片的S参数散射矩阵，通过S参数级联，得到整个波导滤波器的散射参数。

2.1 H面阶梯求解

第一步：模式分析。如图2所示，为一个双边H阶梯的示意图，主模TE10模只有3个场分量（），电场只有分量，并且在y方向是均匀的，在x方向按分布。而波导H面阶梯的y方向是连续的，不连续性发生在x方向上。因此激励起的模式为模，即n>0的那些高次模可以全部不考虑。

又由于该双边H阶梯具有对称结构，由于是偶对称的，因此只能激励起偶模，即模（m=1，3，5…，下文如无特别声明，m都为奇数）。

第二步：模式展开。模的标量波函数为，

将叠加后得到Ⅰ区的横向场分量为：

（1）

分别是前向和后向波的归一化模式电压。是归一化系数，目的是使散射参数小于1。其中：

（2）

（3）

（4）

同样，II区场可表示为

（5）

其中，n为奇数，分别是前向和后向波的归一化模式电压，是归一化系数，且：

（6）

（7）

（8）

第三步：场分量匹配。在不连续处（z=0），场分量匹配的两个必要条件是：

（9）

（10）

因此，有：

（11）

第四步：广义散射矩阵。应用模式正交性，并遵循“电大磁小的原则”有：

（12）

将待入上式，进一步化简得到

（13）

其中，

（14）

用矩阵表示为：

（15）

根据散射矩阵的定义，有：

（16）

其中：

（17）

矩阵元素表示端口j入射的第n个模式时在端口i内第m个模式的传输或反射系数。

第五步：矩阵级联。实际的微波元器件往往是由多个不连续性构成的，将单个不连续性的GSM级联就可以得到多个不连续性的总的GSM[2]。下面以两个不连续性为例进行说明。如果两个不连续性的GSM矩阵分别是SL和SR，如图3所示，则根据散射矩阵的定义，总的散射矩阵为：

（18）

2.2 波导滤波器整体分析

由矩阵级联公式，可以求出整个波导滤波器的GSM矩阵。设最终得到的GSM矩阵为S，即：

（19）

由广义散射矩阵的定义，其主模的散射参数S11，S21分别为子矩阵S11和S21右上角的第一项，根据定义得到：

（20）

（21）

3 数值仿真

采用Matlab编写不同函数功能模块进行求解，并对数值结果进行讨论。

3.1 程序流程

由理论分析，利用Matlab编程实现算法，并绘制波导滤波器S11和S12的扫描特性曲线。程序流程图如图4所示，程序见附录或附件中的M文件。按照模式匹配的严格理论，只有当M，N取无穷大时才能得到严格解[3]，在实际的数值求解中取M=N=10。同时对频率散点扫描，在30～38G之间，取步长为0.08G。

3.2 仿真结果及讨论

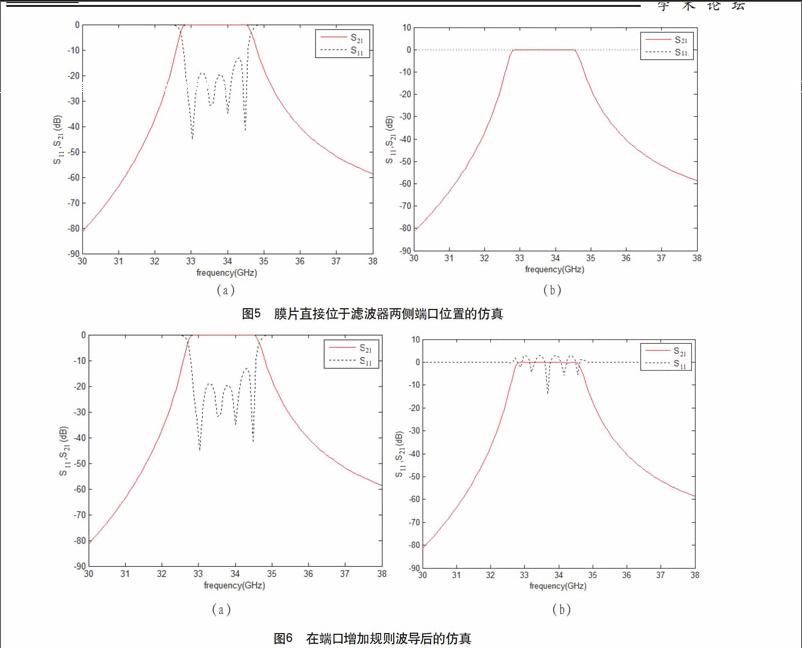
在编程过程中，起初假设膜片直接位于波导滤波器两侧端口位置。由定义式（20）及（21）得到的S11，S21参数曲线如图5（a）所示，在理论上应该有：

（22）

图5（b）是根据定义（21）先算出S21，再根据（22）算出S11参数。对比可以发现，S11在不同的计算方法下具有较大的差异。

原因分析，这是由于入射波在零距离H膜片处就激励起了高次模，在存在N个模式的发射波中只取了主模的反射参数，而丢失了其他模式的能量，因而此时S11不满足式（21）的能量守恒关系。

为此在波导滤波器的端口增加若干个波导波长的长度。增加端口后的散射参数如图6所示，其中图6（a）由公式（20）、（21）得到，图6（b）由公式（21）及（22）得到。对比可知：两组图的结果有所接近，但仍存在差异。这在一定程度上说明在波导滤波器端口增加一段规则波导长度，能使信号高次模有明显的衰减。

又波导滤波器具有对称结构，理论上认为当主模激励时，高次模为偶模。为此编写程序进行验证，此时取M=N=5，即分别取5个偶模，仿真结果如图7（a），考虑到相同的计算精度，与同时取5个奇模和5个偶模的情况对比，结果表明两者相差较大。若取M=N=10，得图7（b），与图6（a）相一致。结果表明，只取偶模不能降低一半计算量。

由图6（a）及图7（b）分析可知，该波导滤波器的3dB带宽约为32.6～34.5GHz，带内的反射系数均小于0.1。

4 结语

本文通过模式匹配法，对波导滤波器进行Matlab编程求解，得出了滤波器的散参数，对工程实践中波导滤波器的设计具有一定的价值。

参考文献

[1] 唐谦，张大方.入侵检测中模式匹配法的性能分析[J].计算机工程与应用，2005（17）：136-138.

[2] 赵念强，鞠时光.入侵检测系统中模式匹配算法的研究 [J].微计算机信息，2005（12）：22-23.

[3] 朱俊.多模式匹配算法研究[D].合肥工业大学研究生院，2010.endprint