基于T-S模糊神经网络的变形预报研究

成 枢，荆晓宇，李 圳,2

(1．山东科技大学 测绘科学与工程学院，山东 青岛 266510; 2．中国测绘科学研究院，北京 100830)

基于T-S模糊神经网络的变形预报研究

成 枢1，荆晓宇1，李 圳1,2

(1．山东科技大学 测绘科学与工程学院，山东 青岛 266510; 2．中国测绘科学研究院，北京 100830)

T-S模糊神经网络模型是根据模糊系统和人工神经网络优缺点具有明显的互补性结合而成。文中基于T-S模糊神经网络，将其应用于变形预测。通过实测数据和仿真数据分析比较了其与BP神经网络、小波神经网络在预测精度、算法稳定性和有效区间3个评价标准上的优劣。结果表明，在变形预测，特别是利用长周期监测数据进行预报时，T-S模糊神经网络具有一定的优势。

模糊理论；模糊神经网络；变形预测；精度；稳定性；有效区间

随着我国经济的发展，城镇化速度加快，在建筑物施工和使用初期，要周期性地利用监测数据对建筑物变形作出及时预报[1]。随着数据处理技术的发展，神经网络以其较强的容错力、自学习、自组织和自适应等优点，广泛应用于数据预测领域，表现出良好的智能特性[2-5]。但目前变形预报中常用的BP神经网络、小波神经网络等虽然具有较强的非线性拟合能力，但仍然存在着收敛速度慢、误差较大且结果不稳定等缺点，制约其在变形预报中的应用[6]。

模糊数学是用来描述、研究和处理事物模糊特征的一种数学理论[7]。由模糊理论与神经网络结合形成的模糊神经网络不但具有模仿人脑思维逻辑的能力，而且同时具有神经网络良好的非线性描述、擅长处理多变量等优点，成为大量研究学者的研究热点[8]。张正禄等结合滑坡变形实例，指出模糊神经网在工程变形分析和预报中的可行性[9]。肖桂元等将动态模糊神经网络应用于桥梁墩台沉降变形预测，并证明其具有较高的预测精度[10]。卢祥等通过实例验证模糊神经网络具有比其他预报方法更高的预测精度[11]。张广平等通过实验表明T-S模糊神经网络模型具有良好的预测功能[12]。但目前大多数学者的研究多集中在模糊神经网络的预测精度分析，而未探讨利用不同监测周期数据进行预报工作时对精度的影响。而衡量一种变形预报算法的优劣还应当包括算法稳定性、有效区间等指标，同时，利用长、短周期监测数据均应有较高的预测精度。

本文基于实测数据和仿真数据，分析比较T-S模糊神经网络与传统的变形预报数学模型在分别利用长、短周期监测数据时的预报精度，并研究模糊神经网络在算法稳定性和有效区间上的优势。结果表明，T-S模糊神经网络在变形预报工作中具有明显优势。

1 模糊理论

将模糊数学中的隶属度、隶属度函数等概念引入到人工神经网络之中形成T-S模糊神经网络。其中隶属度指的是元素μ属于某个模糊子集f的隶属程度，通常用一个位于区间[0,1]中的数μf(μ)表示，μf(μ)越接近1，则说明μ属于f的程度越大，μf(μ)越接近0，则说明μ属于f的程度越小。模糊隶属度函数则是用于计算子集中某个元素μf(μ)隶属度的函数。

T-S模糊神经网络拥有很强的自适应能力，它通过修正模糊子集的隶属函数来建立新的推理，这种推理是在学习过程中逐渐形成的。若用“if-then”的形式来定义T-S 神经网络，那么在规则为Ri时，推理

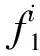
(1)

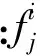
该推理可以视为确定的输出(then)为模糊的输入部分(if)的线性组合。

2 T-S模糊神经网络

2.1 T-S模糊神经网络的结构

T-S模糊神经网络有4层结构：输入层、模糊化层、模糊推理层和输出层。其结构如图1所示。

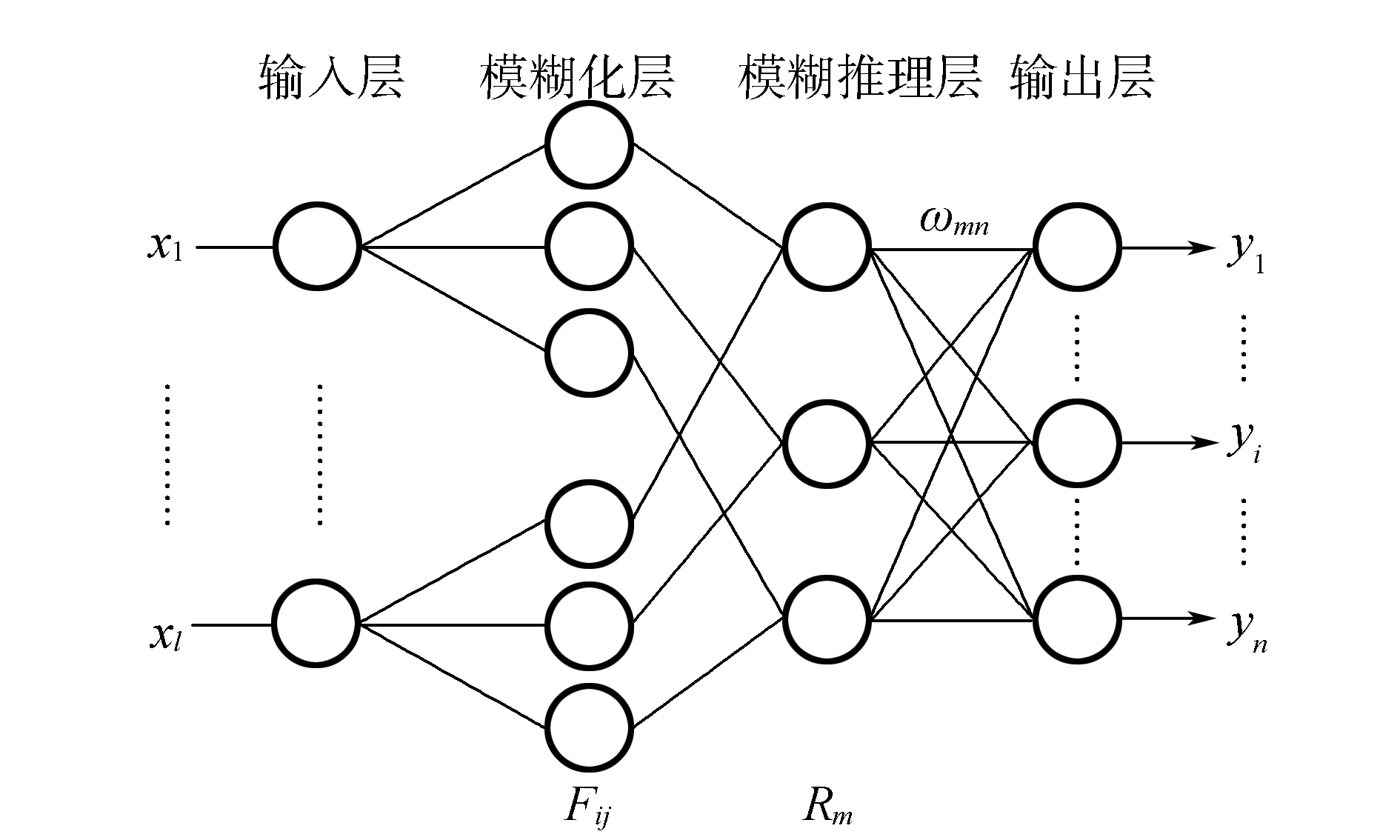
图1 T-S模糊神经网络结构

在图1中，向量为x1,x2,…,xl输入变量；Fij是第i个输入变量的第j个隶属函数；Rm表示第m条模糊推理；ωmn为第m条模糊推理到第n个输出的连接权；y1,y2,…,yn则为网络的输出变量。

1)输入层：该层节点数与输入向量的维数相同，一个输入变量xl对应一个节点，文中设计时间间隔t1，累积沉降量t2，时间间隔t3分别作为输入变量x1,x2,…,x5。此外，输入层还起着将输入数据归一化的作用。

2)模糊化层：每个隶属函数对应一个节点，其作用是计算输入分量属于各变量模糊集合的隶属度函数。因为输入量为时间间隔与累计沉降量，其值一般不会很大，当把隶属度函数的输出压缩到[0,1]区间时，隶属度值对输入值的变化仍然比较敏感。所以使用高斯函数作为隶属度函数，那么对于输入变量x=[x1,x2,…,xl]，输入变量xl的隶属度为

j=1,2,…,l;i=1,2,…,m.

(2)

式中：μij(xi)是xi的第j个隶属函数；cij和σij分别为隶属度函数的中心和宽度。

通过调整cij和σij，可以改变隶属度函数的位置和形状，两者的值通常根据输入样本的不同设定，同时，其值也会随着网络的训练过程向着最适应的趋势。

3)模糊推理层：该层节点数对应模糊规则数，即每个节点代表推理中的“if”部分，它主要用来匹配模糊规则。在本文所建立的变形预报模型中，因为输入变量数不大，其值为5，因输入变量增多导致模糊规则数增长过大引起的网络训练困难现象并不明显。同时考虑到取最大值、取最小值算法均会丢失大量有用信息，使得算法精度降低，所以对隶属度可以使用连乘或累加算法。本文所采用的是连乘算法，那么第j个模糊推理层神经元到第i个输出层神经元的连接权值为

ωij=μj1(x1)μj2(x2)…μjk(xk)，

i=1,2,…,m.

(3)

4)输出层：每一个输出变量对应一个节点，它的作用是通过解模糊化和反归一化实现清晰化计算输出，那么下一期的沉降量即模型的输出值为

(4)

本文所设计的网络中，输入节点数为5；根据文献[7]中相关研究，人为设置输入模糊推理层节点数为12；根据图1所示的网络结构，则模糊化层节点数为12×5=60;输出层节点数为1。因此构建的网络结构为5-60-12-1。

2.2 T-S模糊神经网络的学习算法

T-S模糊神经网络算法流程如图2所示。

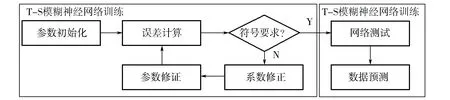
图2 T-S模糊神经网络算法流程

1)初始化网络的各项参数。

2)输入数据进入网络，开始训练网络，并计算期望输出与实际输出的误差为

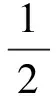
(5)

式中：ye为期望输出；yr为预测输出。

3)判断e是否符合神经网络要求，若不符合要求则继续进行4)、5)，若e符合要求则结束训练过程。由于e不会随着训练次数的增加而无限减小，同时为了避免网络的过度拟合，通常会对训练次数设置上限。一般在变形预报模糊神经网络模型中，训练次数不会超过100次即可得到比较理想的结果，因此设置训练次数上限为100次。

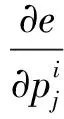
(6)

(7)

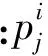
经试验当取0.5时，效果最理想。

5)对隶属数的中心和宽度参数cij，σij进行修正为

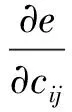
(8)

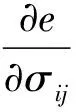
(9)

式中，β为参数学习率。β的选取与α类似，本文选取β的值为0.3。

6)重复步骤2)。

3 T-S模糊神经网络预报分析

3.1 精度分析

1)算例1。在某地基基坑沉降监测项目中，对某观测点共进行32期观测，相邻观测周期间隔在3 d 左右，属于短周期监测。将数据分为两组，一组为前27期的沉降观测数据，用来训练神经网络，另一组为后5期观测数据，用来验证网络的预报精度。

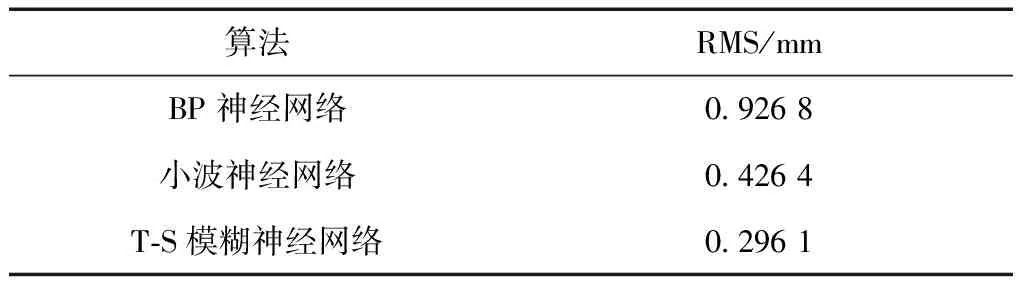
本文基于Fortran编程实现了BP神经网络、小波神经网络和T-S模糊神经网络的变形数据预报，3种算法的预报精度见表1，T-S模糊神经网络预报结果及其与观测值之差见图3，BP神经网络、小波神经网络预报结果及其与观测值之差见图4。

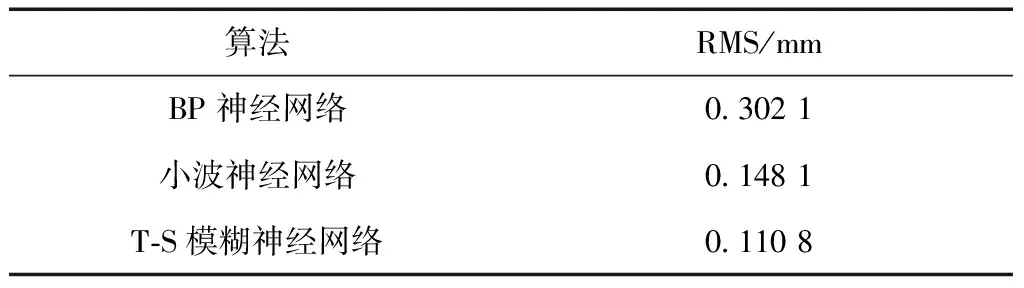
表1 3种算法对基坑沉降的预报精度

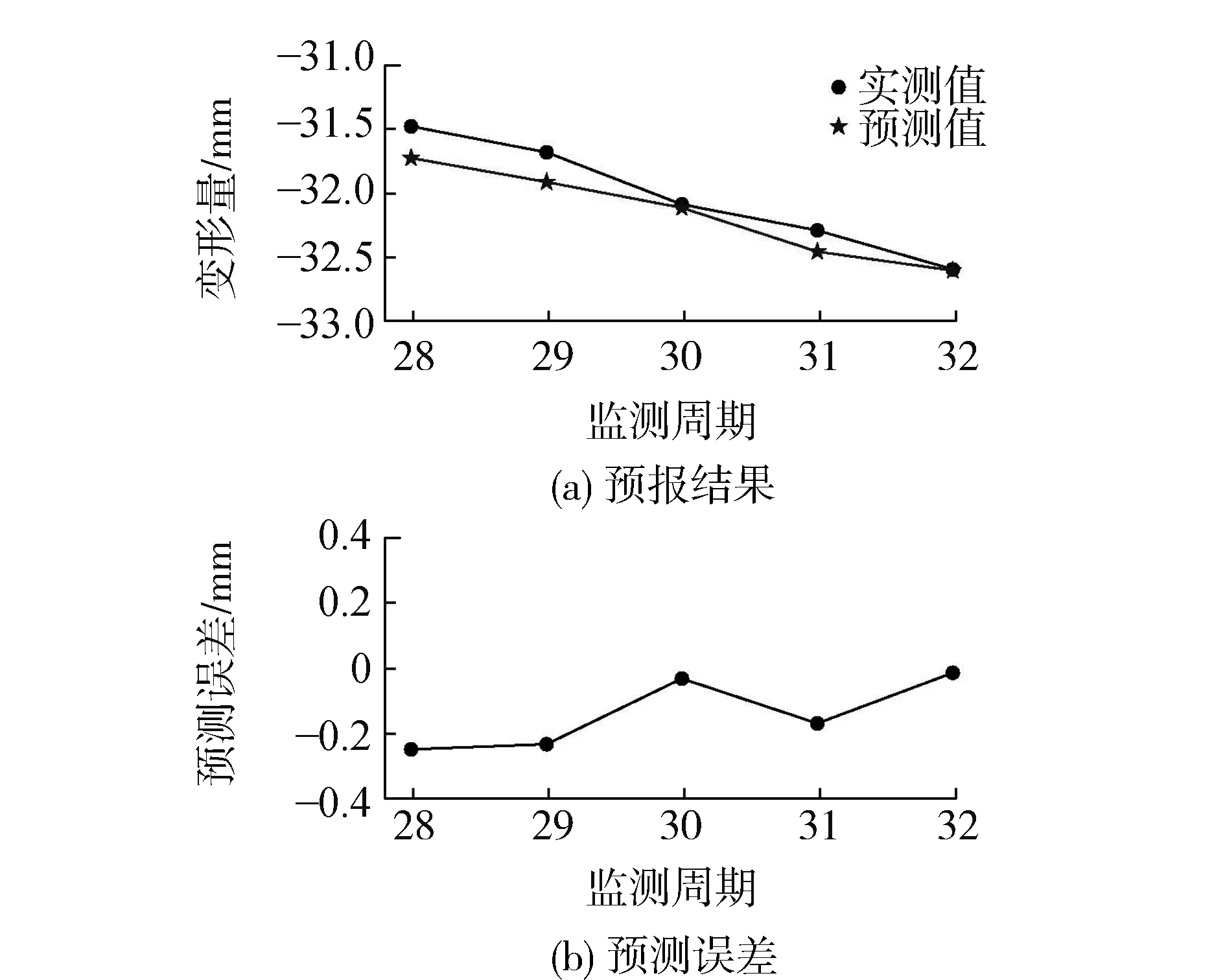
图3 算例1 T-S模糊神经网络预报结果及其与观测值之差

2)算例2。在某地楼座沉降监测项目中，对某个观测点共进行了40期观测，相邻观测周期间隔在20 d左右，属于长周期监测。将数据分为两组，一组为前35期的沉降观测数据，用来训练神经网络，另一组为后5期观测数据，用来验证网络的预报精度。3种算法的预报精度见表2，T-S模糊神经网络预报结果及其与观测值之差见图5。

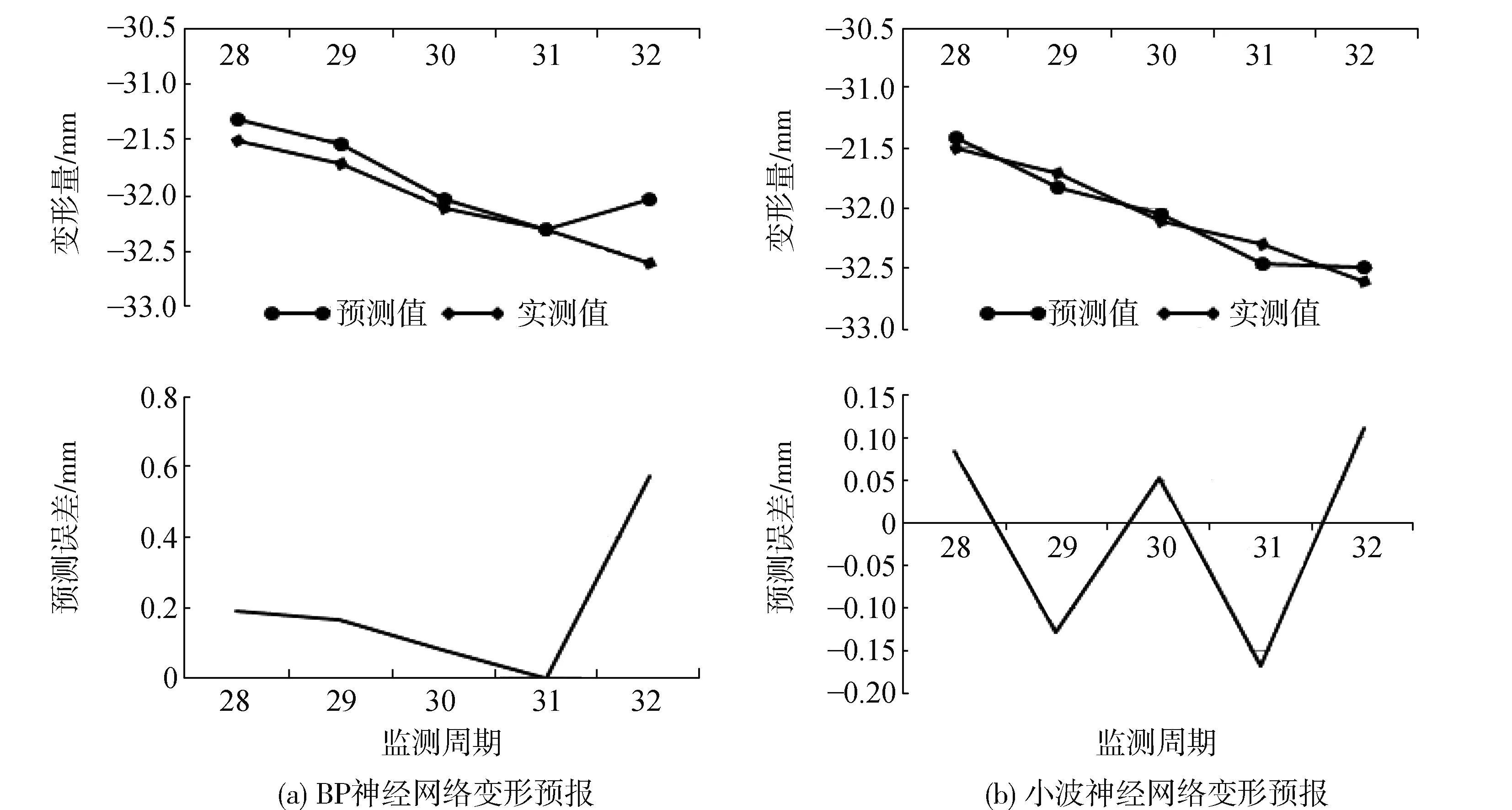
图4 BP神经网络、小波神经网络预报结果及其与观测值之差

算法RMS/mmBP神经网络09268小波神经网络04264T⁃S模糊神经网络02961

图5 算例2 T-S模糊神经网络预报结果及其与观测值之差

由表1、表2可知，在使用T-S模糊神经网络进行变形预测时精度最高，而BP神经网络的预测精度最差，这一结果与其他学者的研究基本一致[9-14]。在对长周期监测数据进行预测时，模糊神经网络的预测精度较高这一特征更加明显，说明T-S模糊神经网络不但在进行短周期变形预报时拥有较高的精度，而且较BP神经网络、小波神经网络更擅长利用长周期监测数据进行变形预报。这与长周期的监测不能像短周期监测提供较为精细的沉降变化趋势，从而使BP神经网络不能同模糊神经网络一样通过不断修正模糊子集的隶属函数更新模糊推理来建立网络有关。

3.2 稳定性分析

由于在实际工程应用中很难获取建筑物变形的先验信息，因此就不能在变形发生前对预报信息作出准确评价，这不但要求建立的数学模型有较高的预测精度，还要有良好的算法稳定性。算法的稳定性指的是算法在相同条件下对同一组数据进行多次预报时的误差变化范围，变化范围小则说明算法的稳定性好，变化范围大则说明算法的稳定性较差。

利用BP神经网络、小波神经网络和T-S模糊神经网络对算例1)中基坑沉降数据分别进行5次预报，分析每次预报的RMS偏差范围，其结果如表3所示。

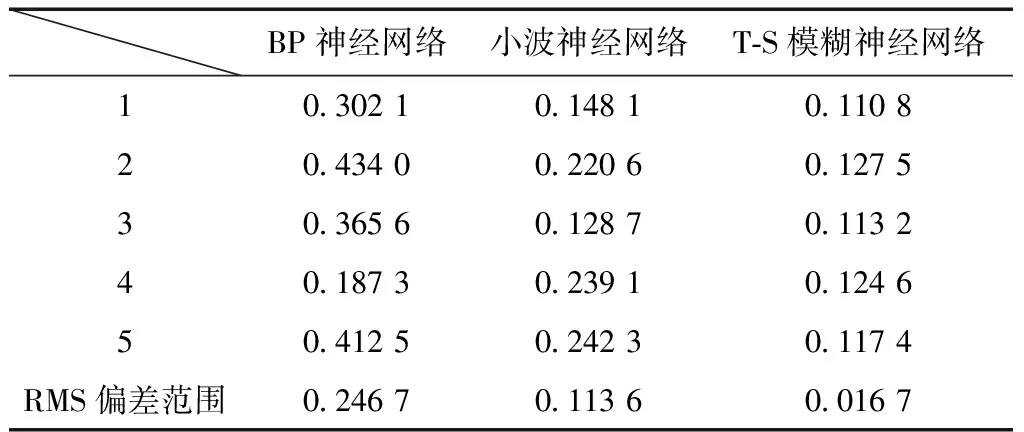
表3 3种算法5次预报的RMS值偏差 mm

由表3中可以看出，BP神经网络不但预报的精度较差，而且其稳定性在3种算法中最差，其RMS偏差范围达到0.246 7 mm。小波神经网络虽然有时也可以达到与T-S模糊神经网络相当的预报精度，但是其计算结果不稳定。而T-S模糊神经网络不但具有较高的预报精度，而且还具有3种算法中最高的稳定性，其RMS偏差范围仅为0.016 7 mm。这说明T-S模糊神经网络较其他两种算法在实际工程应用中更具有可靠性。

3.3 有效区间分析

现模拟一组类似于建筑物沉降曲线的仿真数据如式(10)所示，分别使用3种算法对该组仿真数据进行预报。

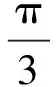
(10)

取模拟数据的前1 000个数，加入服从N(0,0.1)分布的随机误差，相当于以观测精度ε=±0.1观测的1 000个数据。并设定，当数据的预报精度RMS≤2ε时训练数据与预测数据的比值称为预报的有效区间，那么当选取不同数量的训练数据时预报精度如表4所示。

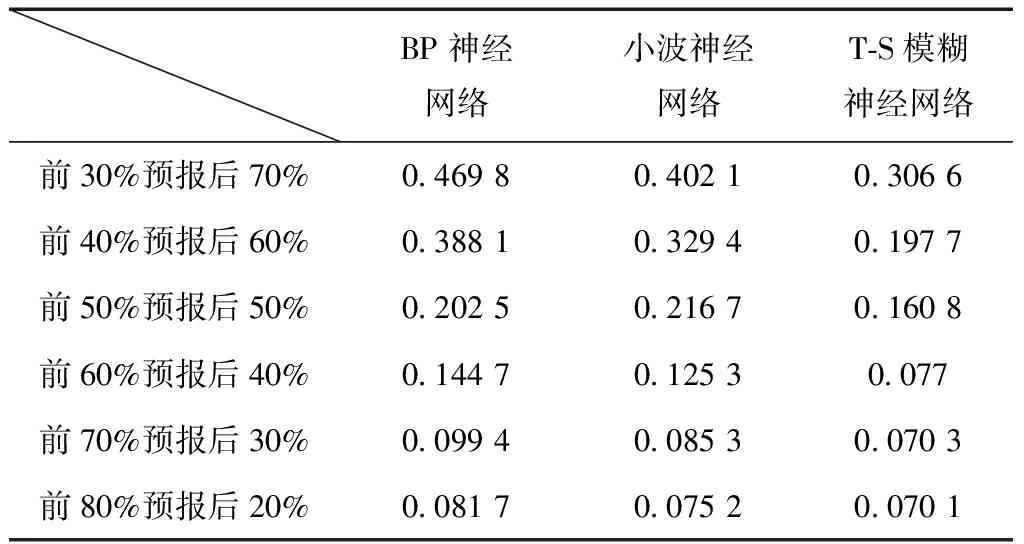
表4 3种算法的预报精度 mm

由表4中可以看出，T-S模糊神经网络的有效区间(前40%预报后60%)明显比BP神经网络(前60%预报后40%)和小波神经网络(前60%预报后40%)的有效区间要长。这说明T-S模糊神经网络可以在使用较小数据量的情况下获得优于BP神经网络和小波神经网络的预报结果，预报长周期变形的能力最强。

4 结束语

建筑物沉降受到多种因素的影响，是一种复杂的非线性时变系统。本文将模糊理论引入到神经网络之中，形成T-S模糊神经网络，将其应用于变形预测工作中。并通过实测数据和仿真数据对BP神经网络、小波神经网络和T-S模糊神经网络的预报精度、稳定性和有效区间三个方面做了比较分析。实验证明，T-S模糊神经网络的预报精度在三种算法中最高，稳定性最好，有效区间最长，而且在利用长周期监测数据进行预报时具有明显的优势。因而T-S模糊神经网络在变形预测工作中具有一定的应用潜力。

[1] 栾元重, 吕法奎, 班训海. 动态变形观测与预报[M]. 北京:中国农业科学技术出版社,2007.

[2] 吕婵. 基于BP神经网络的短期负荷预测[D]. 武汉:华中科技大学,2007.

[3] 李晓杰, 郭睿, 黄金 ,等. 神经网络在北斗导航卫星轨道预报中的应用[J]. 武汉大学学报(信息科学版), 2015, 40(9): 1253-1258.

[4] 范良, 赵国忱, 苏运强. 果蝇算法优化的广义神经网络在变形监测预报中的应用[J]. 测绘通报, 2013(11): 87-89.

[5] 邓勇, 张冠宇, 李宗春, 等. 遗传小波神经网络在变形预报中的应用[J]. 测绘科学, 2012, 37(5): 183-186.

[6] 王小川, 史峰, 郁磊, 等.MATLAB神经网络43个案例分析[M]. 北京:北京航空航天大学出版社,2013.

[7] 李鸿吉.模糊数学基础及实用算法[M]. 北京:科学出版社，2005.

[8] 周琛晖. 模糊神经网络稳定性分析及其应用[D]. 成都:电子科技大学, 2013.

[9] 张正禄,王小敏,邓勇,等. 模糊神经网络在变形分析与预报中的应用研究[J]. 武汉大学学报(信息科学版), 2010,35(1): 6-8,29.

[10] 肖桂元,刘立龙. 动态模糊神经网络在变形预测中的应用[J]. 桂林理工大学学报, 2011(3): 395-398.

[11] 卢祥,马友利,王芳洁,等. 模糊神经网络在变形监测预报中的应用研究[J]. 测绘科学, 2010，35(增1): 113-114.

[12] 张广平,张晨晓,谢忠.基于T-S模糊神经网络的模型在台风灾情预测中的应用[J].灾害学,2013(4):86-89.

[13] 邓兴升,王新洲. 动态神经网络在变形预报中的应用[J]. 武汉大学学报(信息科学版), 2008,33(1): 93-96.

[14] 王新洲,邓兴升. 大坝变形预报的模糊神经网络模型[J]. 武汉大学学报(信息科学版), 2005,30(7): 588-591.

DeformationpredictionresearchbasedonT-Sfuzzyneuralnetwork

CHENG Shu1，JING Xiaoyu1，LI Zhen1,2

(1. College of Geomatics,Shandong University of Science and Technology，Qingdao 266510，China；2. Chinese Academy of Surveying and Mapping，Beijing 100830，China)

T-S fuzzy neural network model is based on the fact that the advantages and disadvantages of fuzzy system and artificial neural network have obvious complementarity,which is used in deformation prediction. Through the analysis of measured data and simulation data, comparison on advantages and disadvantages of three evaluation standards between the T-S fuzzy neural network and BP neural network, a wavelet neural network has been carried out. The three evaluation standards include prediction precision, algorithm stability and effective interval. As a result, in the deformation prediction, especially in the forecasting by using long period monitoring data, the T-S fuzzy neural network has some certain advantages.

fuzzy theory；fuzzy neural network；deformation prediction；precision；algorithm stability；effective interval

著录：成枢，荆晓宇，李圳.基于T-S模糊神经网络的变形预报研究[J].测绘工程，2018，27(1)：37-41.

10.19349/j.cnki.issn1006-7949.2018.01.008

2016-12-02

成 枢(1963-)，男，教授，博士.

TU196

A

1006-7949(2018)01-0037-05

张德福]