修补切口应力强度因子边界元法研究

张永锐, 程长征

(合肥工业大学 土木与水利工程学院,安徽 合肥 230009)

修补切口应力强度因子边界元法研究

张永锐, 程长征

(合肥工业大学 土木与水利工程学院,安徽 合肥 230009)

切口尖端的应力奇异性严重影响了含切口构件的使用安全,采用粘贴材料修补切口后必须对修补效果进行评估。文章利用边界元法对修补切口构件进行数值模拟,运用应力法计算切口尖端的应力强度因子,分析了修补材料的弹性模量、厚度等参数对切口应力强度因子的影响,评估了含切口构件修补后的效果。

切口;应力强度因子;几乎奇异积分;边界元法

含切口构件在结构工程领域有着广泛的应用,例如,钢结构施工过程中需根据实际要求对板材进行局部的切割、焊接构件的焊趾、材料的对接搭接等。切口尖端的应力集中导致结构局部力学性能突变,结构的失效往往起源于切口尖端[1]。应力强度因子是表征切口尖端附近应力场强弱程度的重要参量,对于含切口构件的安全性能进行评估有着重要的意义[2]。对切口进行修补可以有效降低切口尖端的应力强度因子的数值,提高结构的安全性能[3]。切口修补加固的方式也有多种,其中,在开口处粘贴高强度的板材简单易行。因此,对切口粘贴板材的加固方式进行安全评价也显得尤为重要。

切口应力强度因子的获取方法主要有实验法、理论分析法及数值计算法。文献[4]提出了平面V形切口双应力强度因子的光弹性实验研究方法，文献[5]采用渐近特征展开法分析了平面V形切口塑性应力奇异性，文献[6]采用边界元法(boundary element method,BEM)分析了几何特征对含切口构件疲劳寿命的影响，文献[7]采用杂交有限元法分析了热机载荷下多边形夹杂角端部的奇异应力场。尽管对切口尖端的奇异应力分析的文献较多,但对切口修补及其效果评价的研究却很少[8]。

边界元法计算量小，能有效处理应力集中问题并可以根据需要计算任意内点的应力[9]。本文采用边界元法计算含修补切口构件内的应力场,再利用应力法[10]计算修补切口的应力强度因子,研究修补材料的属性、厚度等参数对修补切口应力强度因子的影响。

1 多域边界元法

当运用边界元法分析修补结构时,一般是将结构按照材料的属性划分为多个子结构(子域),在每个子域内分别列边界积分方程,然后根据界面协调条件,将所列边界积分方程耦合起来,即采用多域边界元法。

不失一般性,讨论平面内含2个子域Ω1和Ω2的双域结构,如图1所示。在每个子域,二维弹性力学常规的位移边界积分方程为:

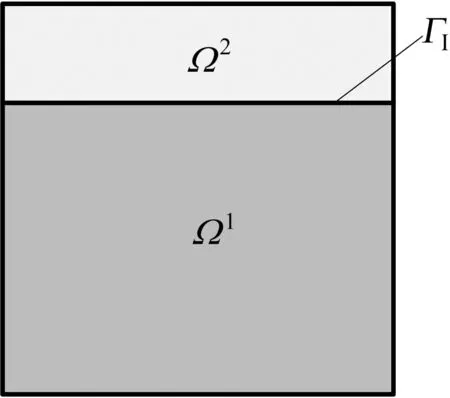
图1 双域结构

对Ω1域列边界积分方程(1)式离散后组装,有

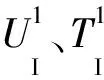
在交界面ΓI上,2个子域对应点的位移和面力应该满足:

根据变形协调关系(4)式,(2)式和(3)式可以组合为:

因为界面上的物理量均未知,所以UI、TI始终落在(5)式的左边,而非交界面上的位移分量U1、U2和面力分量T1、T2,根据问题的实际情况,如果未知,那么放到(5)式的左边；如果已知，那么移到(5)式的右边,最终形成多域边界元法系统方程组,求解后可以计算出边界和交界上所有的未知量。

内点应力边界积分方程为:

利用(6)式可以计算出任意内点的应力值。

若以G表示切变模量、ν表示泊松比,(1)式和(6)式中积分核的表达式分别为:

r,n[(1-2ν)δij+2r,ir,j]}

(8)

r,iδkj-r,jδki)+2r,ir,jr,k]

(9)

ν(r,iδjk+r,kδij)-4r,ir,jr,k]+

(1-2ν)(2r,ir,kn,j+δjkni+δijnk)+

2ν(r,ir,jnk+r,jr,kni)-(1-4ν)δkinj}

(10)

当修补材料比较薄或者内点靠近边界时,源点y到场点x的距离都非常靠近,即r→0,由于(7)～(10)式中r出现在对数项或分母中,导致积分方程(1)式和(6)式会出现几乎奇异积分,常规的高斯积分会使得计算结果失真甚至错误。文献[11]采用反复分部积分的办法,提出了几乎奇异积分的正则化算法,本文采用此法来处理修补切口边界元分析中出现的几乎奇异积分问题。

2 切口应力强度因子的计算

由边界元法计算出内点应力场后,可以采用后处理的方法获得切口的应力强度因子。文献[10]提出了一种计算切口应力强度因子的应力法。对于单应力奇异性的平面问题,在以切口尖端为原点的极坐标系(ρ,θ)中,切口尖端附近的应力场可表示为:

其中,i=ρ,θ,ρθ;j=ρ,θ,ρθ;K为应力强度因子;λ-1为应力奇异指数;fij(θ)为应力角函数。令

可将(11)式改写为:

σij=Aijρλ-1

(13)

对(13)式两边取对数,有

ln|σij|=ln|Aij|+(λ-1)lnρ

(14)

在应力场(11)式的控制区域(即ln|σij|与lnρ成斜率为λ-1的直线段)内沿θ=θ0方向取若干个点ρk(k=1,2,…,N),分别用边界元法计算其应力值σijk,根据最小二乘法,有

(15)式取极小值后,进一步运算可得:

由(12)式和(16)式,可以推导出计算应力奇异指数和应力强度因子的表达式分别为:

λ-1=

因为边界元法引入了几乎奇异积分正则化算法,可以计算非常靠近切口尖端(ρk→0)的内点的应力值,能充分反映切口尖端的奇异应力状态,所以可以运用(18)式计算切口的应力强度因子。

3 数值算例

算例1 单边切口应力强度因子。计算模型如图2所示。切口板宽w=40 mm,长2d=200 mm,边缘均布荷载为P=1 MPa,板材弹性模量E1=206 GPa、泊松比ν1=0.3。切口深度a=8 mm,对称切口的开口角度为2β。

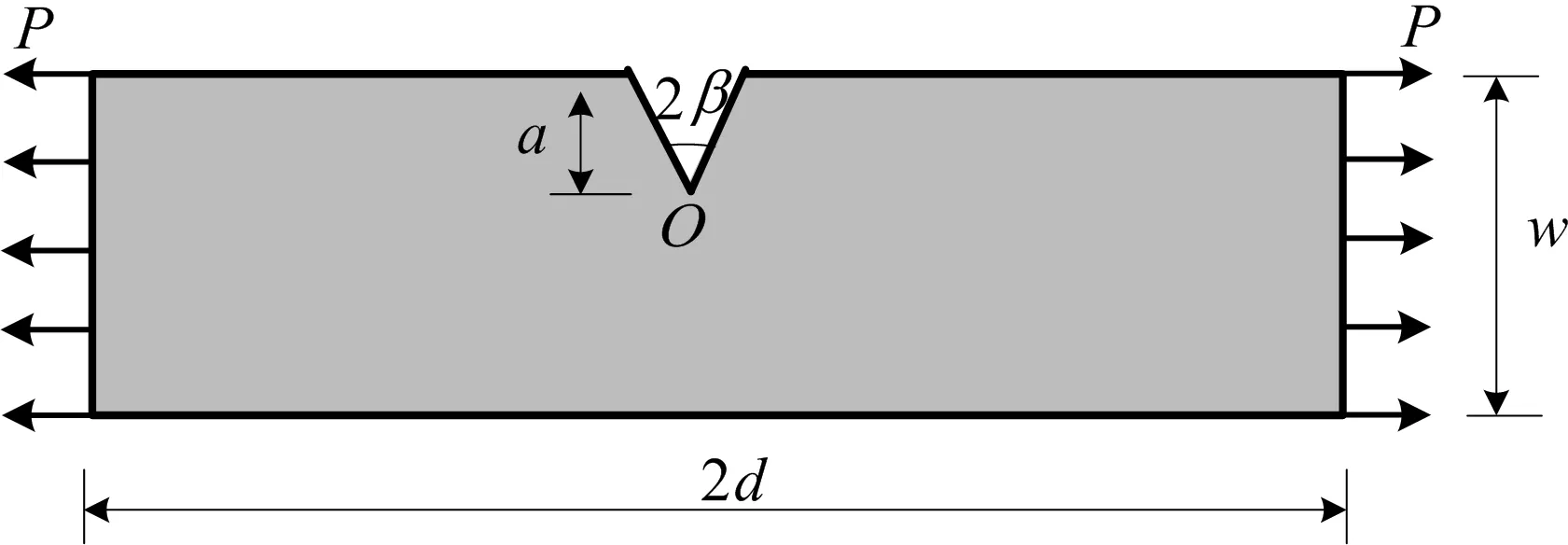
图2 单边切口板

采用边界元法分析，沿着结构边界离散130个线性单元。沿切口角平分线方向选取内点,从距离切口尖端ρ=0.001 mm处开始,等间距取16个内点,间距为0.001 mm。由于所取内点距离边界非常近,计算内点应力值时必须采用几乎奇异积分正则化算法。获取内点应力值后,将这16个点的坐标值ρk和应力值σijk分别代入 (17)式和(18)式,可求得应力奇性指数λ-1和应力强度因子K(单位为N·mm-2-λ)。

为了检验本文算法的准确性,采用有限元法(finite element method,FEM)提供参考结果。在进行有限元模拟时,采用8节点平面单元,总单元数2 113,切口尖端网格划分的最小尺度为5×10-5mm。应力强度因子的边界元法计算结果KBEM、有限元法计算结果KFEM及两者的相对误差见表1所列。

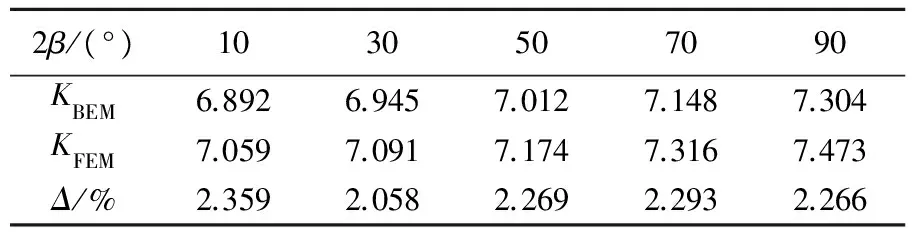
表1 切口应力强度因子边界元法和有限元法计算结果比较

由表1可知,边界元法与有限元法计算结果的最大相对误差小于2.5%,从边界元法和有限元法所用的单元数来看,边界元法的计算量远小于有限元法。

算例2 修补切口应力强度因子。在图2所示的V形切口板外侧粘贴厚度为h的加固层,结构如图3所示。

设定修补层的厚度h=10 mm,修补材料的弹性模量E2=304 GPa，泊松比ν2=0.27。改变切口角度,利用边界元法计算对应的应力强度因子K′,并与未粘贴修补层切口的应力强度因子K进行对比,计算结果见表2所列。

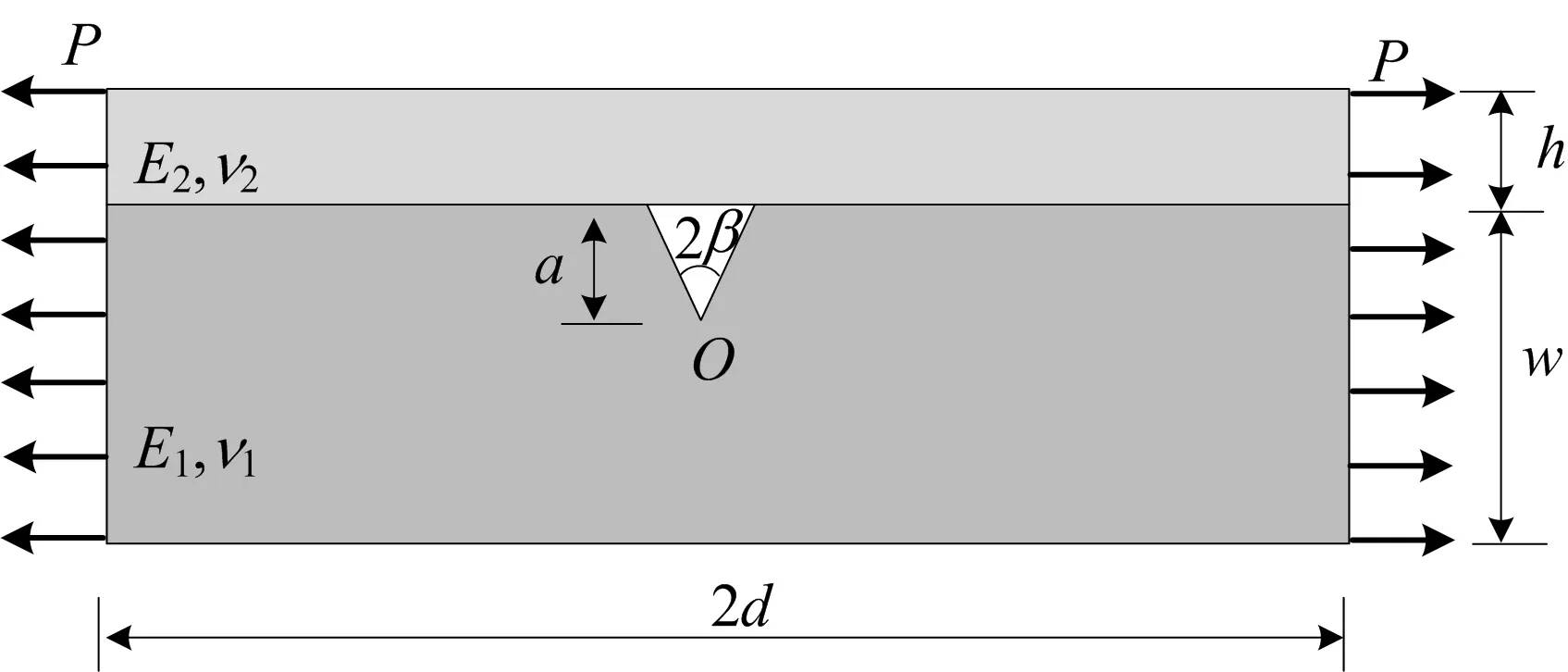
图3 切口外侧修补加固

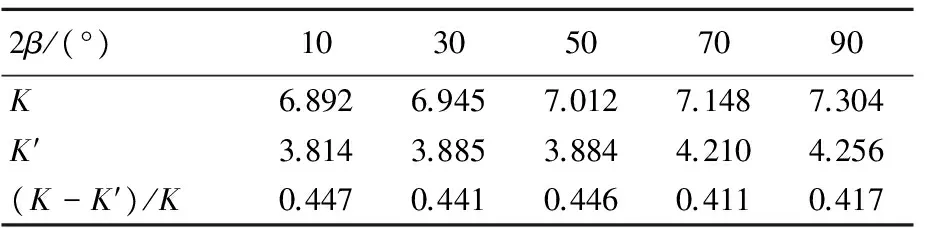
2β/(°)1030507090K6．8926．9457．0127．1487．304K′3．8143．8853．8844．2104．256(K-K′)/K0．4470．4410．4460．4110．417

由表2可知,粘贴修补层之后切口的应力强度因子比粘贴之前有大幅下降,降幅(K-K′)/K最高达到44.66%,可见粘贴修补层后大大提高了结构的抗裂性能。

为研究不同特性的粘贴材料对修补后切口抗裂效果的影响,保持修补层厚度与板宽比h/w=0.1、切口角度2β=90°不变,改变修补材料的弹性模量,分别计算对应修补后切口的应力强度因子,结果见表3所列。

表3 修补材料弹性模量对切口应力强度因子的影响

从表3可以看出,在修补层厚度和切口开角不变的前提下,修补材料的弹性模量越大,对应的应力强度因子越小,说明修补效果越好。但随着弹性模量比的进一步增大(E2/E1>50),应力强度因子减小的幅度逐渐趋于平缓。

选E2/E1=10、2β=90°的切口,研究改变修补材料厚度对切口修补效果的影响,结果见表4所列。由表4可知,在给定的弹性模量比下,随着修补层厚度的增大,切口应力强度因子逐渐减小,但h/w>0.10后应力强度因子的减小幅度不大,因此在该模型下最佳的修补厚度比选0.10。

表4 修补层厚度对切口应力强度因子的影响

4 结 论

本文首先采用边界元法对含切口结构进行数值模拟,然后用后处理的方法确定了V形切口尖端的应力强度因子;运用单一变量法,通过改变修补材料和基材的弹性模量配比、修补层厚度等参数,建立了多种力学模型,以对切口修补效果进行分析。

(1) 粘贴修补层之后切口的应力强度因子较未修补切口有大幅下降,最高降幅可达44.66%。

(2) 修补材料的弹性模量越大,修补效果越好,但随着弹性模量比的进一步增大,应力强度因子减小的幅度并不显著,修补材料与基体材料的最佳弹性模量比为50。

(3) 切口应力强度因子随修补层厚度的增加而减小,但减小幅度随修补层厚度的增加而放缓,最佳的修补厚度比为0.10。

[1] BERTO F,KOTOUSOV A,LAZZARIN P,et al.On a coupled mode at sharp notches subjected to anti-plane loading [J].European Journal of Mechanics-A/Solids,2013,38:70-78.

[2] CARPINTERI A,PAGGI M,PUGNO N.Numerical evaluation of generalized stress-intensity factors in multi-layered composites [J].International Journal of Solids and Structures,2006,43(3):627-641.

[3] KOTOUSOV A,BERTO F,LAZZARIN P,et al.Three dimensional finite element mixed fracture mode under anti-plane loading of a crack [J].Theoretical and Applied Fracture Mechanics,2012,62(10):26-33.

[4] 柳兆涛,刘一华,王炯华.平面V形切口双应力强度因子的光弹性实验研究[J].合肥工业大学学报(自然科学版),2002,25(1):59-62.

[5] 牛忠荣,葛仁余,RECHO N,等.平面V形切口塑性应力奇异性分析[J].中国科学:物理学 力学 天文学,2014,44(1):79-90.

[6] 王强,程长征,张长会.几何特征对含切口构件疲劳寿命的影响[J].合肥工业大学学报(自然科学版),2013,36(3):327-331.

[7] 平学成,徐小翔,陈梦成.热机载荷下多边形夹杂角端部应力场的杂交元分析[J].力学季刊,2014,35(2):283-292.

[8] 章向明,陈礼威,杨少红,等.含裂纹钢板复合材料修补疲劳寿命数值分析[J].海军工程大学学报,2008,20(4):4-7.

[9] 周焕林,徐兴盛,李秀丽,等.反演二维瞬态热传导问题随温度变化的导热系数[J].应用数学和力学,2014,35(12):1341-1351.

[10] LIU Y H,WU Z G,LIANG Y C,et al.Numerical methods for determination of stress intensity factors of singular stress field [J].Engineering Fracture Mechanics,2008,75(16):4793-4803.

[11] 牛忠荣,胡宗军,葛仁余,等.二维边界元法高阶元几乎奇异积分半解析算法[J].力学学报,2013,45(6):897-907.

Analysisofstressintensityfactorsofrepairednotchcomponentsbyboundaryelementmethod

ZHANG Yongrui, CHENG Changzheng

(School of Civil and Hydraulic Engineering, Hefei University of Technology, Hefei 230009, China)

The stress singularity at the notch tip has seriously threatened the safety of notch components. After pasting a plate to repair a notch component, the repairing effect should be studied and estimated. Herein, the boundary element method(BEM) is applied to modeling the repaired notch component. The stress method is then adopted to calculate the stress intensity factor of the V-notch. The effect of elasticity modulus and thickness of the repairing material on the stress intensity factor of the repaired V-notch is investigated. The repairing effect of the notch component is estimated.

notch; stress intensity factor; nearly singular integral; boundary element method(BEM)

2016-03-09；

2016-05-16

国家自然科学基金资助项目(11372094)

张永锐(1991-),男,山东日照人,合肥工业大学硕士生;

程长征(1979-),男,安徽太湖人,博士,合肥工业大学教授,博士生导师,通讯作者,E-mail:changzheng.cheng@hfut.edu.cn.

10.3969/j.issn.1003-5060.2017.12.014

O343.4

A

1003-5060(2017)12-1655-04

(责任编辑张淑艳)