滑坡锚索框架梁的极限位移分析

张延磊，倪万魁，李焕焕

(1.中交第一公路勘察设计研究院有限公司，陕西 西安 710068；2.长安大学地质工程与测绘学院，陕西 西安 710054)

滑坡锚索框架梁的极限位移分析

张延磊1，倪万魁2，李焕焕2

(1.中交第一公路勘察设计研究院有限公司，陕西 西安 710068；2.长安大学地质工程与测绘学院，陕西 西安 710054)

为了对滑坡锚索框架梁锚固工程设计提供依据，以前人所做模型试验为基础开展研究工作。首先，基于锚索框架梁的设计理论—Pasternak(巴氏)双参数地基模型，对梁上弯矩与位移的理论表达式进行简化，然后，采用公式拟合的方法，建立了框架位移阈值与最大弯矩、基床系数、剪切模量、混凝土弹性模量、截面宽度和高度、锚索间距、梁长的关系式，从而得到了极限位移表述式，并利用模型试验实例证明了所建极限位移公式的合理性。这样一来，只要确定滑坡相关参数与框架梁的设计参数，就可以计算出框架位移阈值，评价工程安全程度。

锚索框架梁；Pasternak双参数地基模型；最大弯矩；位移阈值

0 引言

目前，锚索框架梁的理论研究远滞后于工程实践，至今也没有相关的规范为其设计计算提供依据，但是国内很多学者都对锚索框架梁进行了一定的研究。杨明等[1]、肖世国等[2]、刘小丽等[3]、曹兴松等[4]、梁瑶等[5]针对锚索框架梁的内力与设计计算方法开展了研究工作；丁秀美等[6]、吴礼舟等[7]、张华等[8]对锚索框架的数值分析方法进行了研究；马迎娟等[9]、陈春利[10]则通过模型试验研究了锚索框架梁的受力特点和破坏形式。目前仍然缺少的是对锚索框架梁极限位移方面的研究。

自从西部大开发战略开展以来，陕西高速公路发展迅速，截止2012年底，陕西高速公路通车里程突破4000 km，但滑坡等灾害[11-12]也相继增加，滑坡路段的稳定性已成为影响高速公路安全运行的关键因素。近10年来，锚索框架梁在高速公路边、滑坡加固中应用非常广泛[13-14]，为了优化工程设计建立锚索框架梁极限位移变得尤为重要。

1 理论基础

Pasternak(巴氏)双参数弹性地基模型采用了两个独立的参数来表征地基的特性，即基床系数和剪切模量，它是给Winkler地基模型中的弹簧加上约束，以反映地基的连续性，即用一层只能产生剪切变形而不能产生压缩变形的剪切层来连接各个弹簧，故它考虑了地基中应力的扩散，计算值更接近真实值，模型示意图见图1。

本文采用巴氏双参数弹性地基模型，为了计算方便，对文献[16]基于初参数法得到的弯矩与位移表达式进行简单处理，结果如下：

(1)

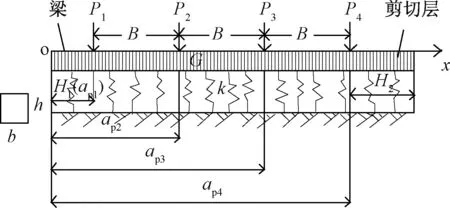
图1 巴氏模型计算示意图Fig.1 Sketch of the calculation of Pasternak model

式中：E——混凝土弹性模量/kPa；

I——截面惯性矩/m-4，I=bh3/12；b——截面宽度/m；

h——截面高度/m；

G——剪切模量/(kN·m-1)。

塞尔瓦多雷建议参考公式:

(2)

式中：k——基床系数/(kN·m-3)；

μ——压缩层泊松比；

h1——压缩层厚度/m；

B—锚索间距/m；

b*、λ、γ、ρ、φ1、φ2——中间参数，表达式详见文献[16]。

F1(x)～F5(x)为关于坐标x的函数，具体表达式见(3)式；api为第i根锚索到梁端的距离；y0、θ0为初始参数，计算方法及结果见文献[16]；Pi为第i根锚索分配到梁垂直方向上的锚固力/kN，锚固力分配公式参考文献[17]；j为计算截面左侧集中荷载的个数，j=0时，P0=0。

(3)

2 极限位移的建立

对预应力锚索框架梁来说，在工作阶段，同条梁上锚索的锚固力一般是不同的，但是对于横梁来说，由于各锚索深入的土层基本一致，设计时张拉预应力一般相同，故各锚索贡献的锚固力有可能是相同的。

由文献[16]中y0与θ0的表达式可知，当锚索锚固力相同时，即Pi=P，i=0,1,2,3…n，y0与θ0含有公共系数P，即有：

y0=y1·P，θ0=θ1·P

(4)

同理，弯矩与位移的表达式可以改写成：

M(x)=P·T1(x)，y(x)=P·T2(x)

(5)

因此，框架梁位移与弯矩的关系式可以写成：

(6)

其中，T1(x)、T2(x)如(7)、(8)式所示，y1、θ1可根据表达式(4)由文献[16]得到。

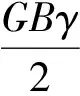
(7)

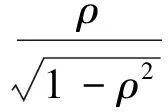
(8)

由(6)式知，在锚固力相同的情况下，当最大弯矩与最大位移位于梁上相同位置时，二者关系式可由(6)式表示。实际上，弯矩最大值一般都位于锚索节点处，但位移最大值往往是位于跨中或节点处，故当位移最大值位于跨中而不是节点处或者位移最大值也位于节点处但其位置与最大弯矩位置不同时，二者关系就不能由式(6)表示。同理，对于锚固力不同的情况，最大弯矩与最大位移的关系式也不能由理论公式推导得到。

为了建立适用于一般情况的框架位移极限位移式，本文采用公式拟合的方法。针对模型试验，输入并调整相关参数，得到所需弯矩最大值与位移最大值，然后，利用1stOpt软件进行数据拟合，最终得到框架梁位移阈值的表达式(9)，其拟合的相关系数为0.999 99。

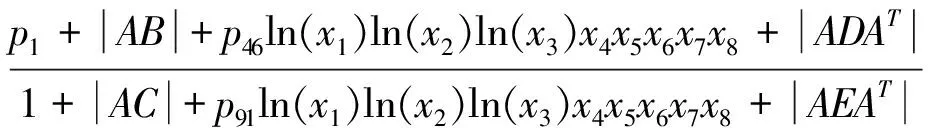
(9)

式中：x1——基床系数；

x2——混凝土弹性模量；

x3——剪切模量；

x4——截面宽度；

x5——截面高度；

x6——锚索间距；

x7——梁的长度；

x8——结构所能承受的最大弯矩；

ycr——位移临界值(阈值)。

式(9)中，p1～p91为拟合系数，详见表1，A、B、C、D、E表达式如下：

A=[ln(x1),ln(x2),ln(x3),x4,x5,x6,x7,x8]；

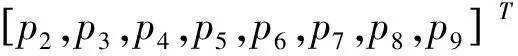
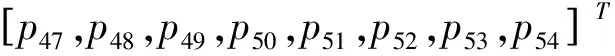
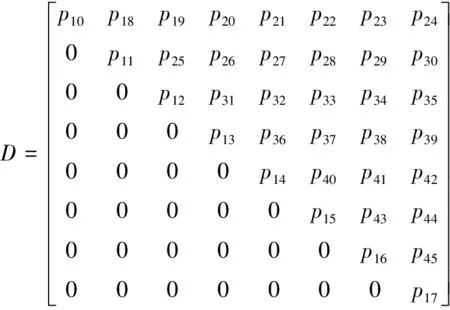
上述拟合公式是建立在模型试验的基础上，适用于小模型尺寸，根据公式的建立过程可知，参数取值范围不同，拟合出的公式适用条件也就不同，因此，我们可以针对不同的滑(边)坡锚索框架梁，建立相适应的极限位移，这样也能提高拟合精度。

假定y测表示纵、横梁垂直方向上的实测位移，ycr表示位移临界值(阈值)，Fs表示安全储备系数，则滑坡锚索框架梁的极限位移可表示为：

y测≥ycr/Fs

(10)

3 实例验证

采用文献[10]的格构梁失效模型试验数据来验证极限位移：

试验中滑床及滑体均采用均质黄土分层夯筑，选用圆弧状滑带，用双层聚乙烯薄膜模拟滑带。试验采用 3×4 跨格构，横梁跨距为1.5 m，竖梁跨距1 m。格构梁截面尺寸100 mm×125 mm。为了测试格构梁变形性能，分析其破坏模式，降低了格构梁的强度。梁内配筋采用Φ8，箍筋采用 2 mm 铁丝，间距为200 mm，混凝土强度为 C10，锚杆与水平方向夹角20°，格构梁尺寸及配筋图、锚杆布置图详见文献。试验中在格构梁内上下同侧钢筋对应粘贴了电阻应变计，测量了格构梁上、下侧的应变。

表1 拟合系数一览表Table 1 Fitting coefficients

根据公式，可以间接计算出格构梁的弯矩：

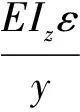
(11)

(12)

式中：M——格构梁的弯矩；

ε——格构梁的应变；

ε1、ε3——钢筋上侧应变；

ε2、ε4——钢筋下侧应变；

y——应变测点到中心轴的距离。

据文献所述，加载36 kPa时格构锚固达到承载力极限状态，由横梁1弯矩图知，此时横梁1的最大弯矩Mmax为2 kN·m，根据式(11)反算出加载36 kPa 时格构梁的最大应变：

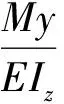
=0.000 298 423

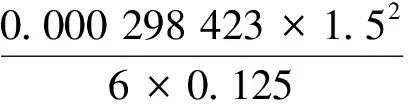
根据格构梁截面尺寸与配筋图，可由下式计算出结构能承受的最大弯矩：

1.95 kN·m

根据模型试验设计资料，参数取值如下：k=5×104kN/m3，E=1.75×104MPa,(压缩层厚度h1取平均值2.3 m，黄土泊松比μ=0.44)，故G=kh12(1-2μ)=5 290 kN/m，b=0.1 m，h=0.125 m，B=1.5 m，L=4.6 m。将Mmax(1.95 kN·m)、k、E、G、b、h、B、L代入到拟合公式(9)中，计算出临界位移ycr=0.862 mm。而试验监测得到的临界状态下的位移为y测=0.895 mm。二者误差Δy=0.033 mm，相对误差为3.7%，显然误差在合理的范围内，而且拟合结果是保守的，这从预警的角度证明了拟合公式是合理的，同时也证明了所建极限位移的合理性。

4 结 论

本文基于锚索框架梁的设计计算方法，分析了梁上最大弯矩与位移临界值关系的复杂性，并利用软件拟合出位移阈值与结构所能承受的最大弯矩的关系式，从而建立了滑坡锚索框架梁极限位移表达式。针对不同的边、滑坡，调整拟合参数，可以建立不同适用条件的极限位移表达式，将该极限位移与边、滑坡框架梁位移监测相结合，还应用到高速公路边、滑坡监测预警系统中，对高速公路的安全运行有重要的实际意义。

[1] 杨明,胡厚田,卢才金,等.路堑土质边坡加固中预应力锚索框架的内力计算[J].岩石力学与工程学报，2002,21(9)：1383-1386.

YANG Ming, HU Houtian, LU Caijin,et al. Caculation of internal forces for prestressed anchor cable frame used in reinforced roadcut soil slope[J]. Chinese Journal of Rock Mechanics and Engineering，2002，21(9): 1383-1386.

[2] 肖世国，周德培．岩石高边坡一种锚索格构型地梁的内力计算[J]．岩土工程学报，2002，24(4)：479-482.

XIAO Shiguo, ZHOU Depei. A calculation method for internal force of prestressed anchor-rope and frame beam-on-foundation on high rock slope[J]. Chinese Journal of Geotechnical Engineering, 2002, 24(4)：479-482.

[3] 刘小丽，张占民，邓建辉.边坡加固中预应力锚索地梁极限状态设计方法[J].岩土力学，2004，25(10)：1617-1621.

LIU Xiaoli, ZHANG Zhanmin, DENG Jianhui. A method for limit state design of foundation beam with prestressed anchor-cable used in reinforced slopes [J]. Rock and Soil Mechanics, 2004, 25(10):1617-1621.

[4] 曹兴松,周德培.软岩高边坡预应力锚索框架梁的一种新型设计方法[J].公路交通科技,2004,21(8)：25-28.

CAO Xingsong, ZHOU Depei. A new design method of prestressed anchor rope framework for high slope in weak rockmass[J]. Journal of Highway and Transportation Research and Development, 2004, 21(8):25-28.

[5] 梁瑶,周德培,赵刚.预应力锚索框架梁支护结构的设计[J].岩石力学与工程学报,2006,25(2)：318-322.

LIANG Yao, ZHOU Depei, ZHAO Gang. Design of support of frame beam and prestressed anchor[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(2):318-322.

[6] 丁秀美，黄润秋，臧亚君.预应力锚索框架作用下附加应力的FLAC3D模拟[J].成都理工大学学报(自然科学版)，2003，30(4)：339-345.

DING Xiumei，HUANG Runqiu，ZANG Yajun. Three dimension simulation with FLAC3Don the subsidiary stress induced by frame beam with prestress cable [J]. Journal of Chengdu University of Technology (Science & Technology Edition), 2003, 30(4):339-345.

[7] 吴礼舟，黄润秋.锚杆框架梁加固膨胀土边坡的数值模拟及优化[J].岩土力学，2006，27(4)：605-608.

WU Lizhou, HUANG Runqiu. Numerical simulation and optimum design of anchor frame beam strengthening expansive soil roadcut slope[J]. Rock and Soil Mechanics，2006，27(4)：605-608.

[8] 张华，陆阳，程强.岩质边坡锚杆(索)框架梁加固的数值模拟[J].公路交通科技，2008，25(1)：21-26.

ZHANG Hua, LU Yang, CHENG Qiang. Numerical simulation of reinforcement for rock slope with rockbolt (anchor cable) frame beam[J]. Journal of Highway and Transportation Research and Development, 2008，25(1)：21-26.

[9] 马迎娟.预应力锚索格构梁复合结构的模型试验研究[D].成都：成都理工大学，2005.

MA Yingjuan. Study on complex structure model experiment of prestressed anchor-rope and lattice beam[D].Chengdu: Chengdu University of Technology, 2005.

[10] 陈春利.滑坡格构锚固防治工程大型物理模拟试验研究[D].西安：长安大学，2014.

CHEN Chunli. Model test research on lattice beam anchorage in landslide reinforcement [D].Xi’an: Chang’an University, 2014.

[11] 黄建榕.陕西户-洋高速公路地质灾害危险性评估[J].灾害学，2003，18(3)：39-45.

HUANG Jianrong. Evaluation of geological hazards along Huxian-Yangxiang free way in Shaanxi[J]. Journal of Catastrophology，2003，18(3)：39-45.

[12] 章健，潘春雷，龙建辉，等.陕-甘G312高速公路彬县滑坡群稳定性数值分析[J].中国地质灾害与防治学报，2007，18(4)：11-14.

ZHANG Jian，PAN Chunlei，LONG Jianhui，et al. Numerical analysis on the Binxian county landslide group stability along Shanxi-Gansu G312 Expressway[J]. The Chinese Journal of Geological Hazard and Control，2007，18(4)：11-14.

[13] 孙英勋.云南山区高速公路滑坡治理研究[J].公路交通科技,2005,22(4)：49-52.

SUN Yingxun. Study on expressway landslides treatment in Yunnan [J]. Journal of Highway and Transportation Research and Development, 2005,22(4)：49-52.

[14] 汪晓锋，黄绍槟.四川西-攀高速公路山神庙隧道进口滑坡综合治理[J].中国地质灾害与防治学报，2007，18(4):15-18.

WANG Xiaofeng，HUANG Shaobin. Comprehensive restraint works of landslide hazard at Shanshenmiao tunnel entrance on Xichang-Panzhihua Expressway in Sichuan Province[J]. The Chinese Journal of Geological Hazard and Control，2007，18(4):15-18.

[15] 隋海波，施斌，张丹，等.边坡工程分布式光纤监测技术研究[J]. 岩石力学与工程学报，2008，27(S2): 3725-3731.

SUI Haibo，SHI Bin，ZHANG Dan，et al. Study on distributed optical fiber sensor-based monitoring for slope engineering[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(S2):3725-3731.

[16] 周志刚.预应力锚索格构梁加固边坡的优化设计及安全系数计算[D].浙江:浙江大学,2011.

ZHOU Zhigang. Optimization design and safety factor calculation of the slopes reinforced by pre-stressed anchors and frame beams[D].Zhejiang: Zhejiang University,2011.

[17] 周景星，李广信，虞石民，等. 基础工程(第二版)[M].北京：清华大学出版社，2007.

ZHOU Jingxing, LI Guangxin, YU Shimin, et al. Foundation Engineering (Second Edition)[M]. Beijing: Tsinghua University Press，2007.

Analysisofmaximumdisplacementofanchor-cableandframebeamagainstlandslide

ZHANG Yanlei1，NI Wankui2，LI Huanhuan2

(1.CCCCFirstHighwayConsultantsCo.,LTD.,Xi’an,Shaanxi710068,China；2.Chang’anUniversity,SchoolofGeologyEngineeringandGeomatics,Xi’an,Shaanxi710054,China)

To optimize design of anchor-cable and frame beam against landslides, the research was carried out based on previous model tests. First, based on the design theory of anchor-cable and frame beam which is Pasternak two-parameter foundation model, theoretical expressions of the moment and displacement were simplified for calculation. Then, by method of fitting the formula, the relation between the displacement threshold of frame beam and maximum moment, coefficient of subgrade, shear modulus, elastic modulus of concrete, width and height of section, anchor spacing and length of beam was established, and the maximum displacement was attained according to the relation, which was proved reasonable by the model test case. In this way, as long as related parameters of the landslide and design parameters of the frame beam were both established, we can calculate the displacement threshold. Combining the displacement threshold with deformation monitoring data of the frame beam, we will achieve the purpose of early warning and forecasting.

anchor-cable and frame beam; Pasternak two-parameter foundation model; maximum moment; displacement threshold

10.16031/j.cnki.issn.1003-8035.2017.04.14

P694

A

1003-8035(2017)04-0084-05

2016-12-14;

2017-09-04

省级国有资本经营预算科技创新专项资金项目(2013gykc-018);陕西省交通运输厅2013年度科研项目(13-28K)

张延磊(1990-)，男，硕士研究生，主要从事地质灾害、岩土工程等方向的研究。E-mail:765646411@qq.com

倪万魁(1965-)，男，教授，博士生导师，研究方向为岩士力学、非饱和土力学等。E-mail:1326763493@qq.com