数学中的集合问题

黄晶鑫

数学中的集合问题

黄晶鑫

高中数学中的集合是高中数学的重要构成部分之一，学生在集合的学习中存在一些问题，需要找到相应的学习策略。本文通过阐述集合学习存在的问题，重点分析研究了学习集合的具体方法策略，希望为广大高中生提供参考。

高中数学的学习中，集合的学习也是一个重点。集合作为一种数学语言，可以简洁准确地表达数学知识，也能被应用在生活中促进一些问题的解决。集合的学习不是仅仅局限在集合的学习上，集合涉及的数学知识范围比较广。所以，高中生在学习集合知识的时候，或多或少存在一些问题，需要通过对集合知识的掌握，提高集合学习的成绩，促进其他知识的学习。

集合学习存在的问题

对集合相关概念掌握不够。集合的学习，首先就是对集合相关概念的学习掌握。因为集合相对来说其概念比较抽象，也存在大量的比较复杂的数学符号和相关的专业术语。这些符号和专业属于都是比较容易混淆，一旦在解题中出现概念混淆，就会直接导致题目解析错误。例如，分不清并集和交集的概念，分不清子集和真子集的区别，就会在实际的解题中出错。长此以往，会形成一个错误的解题思维，导致失分，甚至会对以后其它知识的学习带来影响。

对集合相关性质不清楚。集合和其它知识点不同的是，集合是对一些对象的统称，集合对象是这个集合的元素。集合有三个重要的性质，分别是：第一，集合的确定性，即任何一个集合中的元素是确定的，对具体是哪些元素组成这个集合是确定的，不是模糊不清的存在。第二，集合中的元素还要满足互异性这个条件，也即是说，集合中的元素是互不相同的，同样的元素只能被视为同一元素。第三，无序性，集合中的元素没有排列的顺序，不分排列的先后顺序，都是一致的。

集合学习的策略

掌握集合的相关概念，学会使用相关集合符号。掌握集合的概念和掌握集合符号，最重要的就是通过对具体的集合题目的实践练习。例如，在掌握自然数集和实数集的时候，容易出对N和R等字母所具体代表的是哪一个集合产生混淆。但是，如果学生可以对具体的例子进行记忆，就很容易分清楚。再有就是学生容易对代表集合与集合之间关系的符号产生混淆，更容易产生混淆的是对一些逻辑连接词所蕴含的意义不清楚，容易把生活中的用法带入到集合的学习过程中。因为在实际生活中“或”字，就是表一种选择，是非此即彼的意思，而在集合中若是用“或”字连接的两个集合，就表示“都”的意思。有“一起，全部”的意思，或字连接的两个集合，表示取并集，采用的集合符号是“∪”。而与之相反的就是“且”，在生活中，这个字表达的有一种“和，一起”的意思，但是在集合中，表示的确是交集，只能取两个集合之间共同的部分，采用的集合符号是“∩”。

加强对三种集合语言的练习。集合上使用的集合语言，由于比较抽象，对于部分学生的学习和掌握是一个难点。这就要转换集合语言，把本来抽象的集合语言转换为比较具体，容易理解的集合语言。一般来说，常见的几种集合语言主要是文字语言、符号和图形语言。文字语言就是用文字描述集合之间的关系，符号语言就是用数学上约定的符号来表示集合之间的关系，图形语言就是用图形表示集合之间关系。单独理解这几种符号语言相对来说比较简单，但是要实现互相的转换就没那么简单。

例如，题目告诉高一三班有40名学生，喜欢体育的有25人，喜欢音乐的有20人，两种都喜欢的有10人，求高一三班中两门课都不喜欢的学生人数。那么，在解题中，就要把文字语言转换成方便求解的符号语言。把喜欢体育的学生设为集合A，把喜欢音乐的学生设为集合B，而高一三班这个集体设为全集U，那么，题目中，两种课都喜欢的学生，用集合表示就是：A∩B，而在此条件下，两者都不喜欢的就相应表现成CUA∩CUB。而相应转换成图形语言，就有，如图1所示：

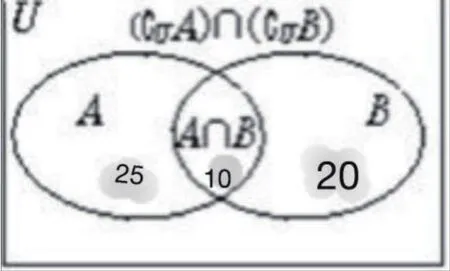
图1

掌握两种常见的解题思维。学生在学习集合的过程中，只有掌握正确的解题方法，才能达到事半功倍的学习效果。常见的有类比思想、数形结合的思想。类比思想就是在学习集合的过程中，对比较难以理解的知识点，通过联系以往学习过的类似知识点来促进理解。比如，学生在学习集合与集合之间关系的过程中，就可以通过借鉴初中学习的数和数之间的相等或者不相等关系，来促进对几个集合之间关系的理解。从而可以联系到不相等的且更小范围的一个集合就是属于另一个更大范围的集合。数形结合的思想是另一种，在学习过程中常见的学习方法。因为集合的某些表达方式比较抽象，学生无法通过文字或者符号的形式实现对该集合题目的理解，这就需要结合图形，借助图形来加深理解。

高中数学的学习对于高中生的升学考试和接下来的继续教育学习都很重要，集合的学习在高中数学中占据的比例也比较大，渗透的内容比较广。但是在集合学习过程中或多或少存在一些问题，这就需要学生掌握一定的学习策略，促进数学成绩的提高。

长沙市第十五中学）