大型民用飞机尾旋运动的系统辨识研究

颜 巍 黄灵恩 黎先平 / YAN Wei HUANG Lingen LI Xianping

(上海飞机设计研究院，上海 201210)

大型民用飞机尾旋运动的系统辨识研究

颜 巍 黄灵恩 黎先平 / YAN Wei HUANG Lingen LI Xianping

(上海飞机设计研究院，上海 201210)

为了研究某常规布局大型民用飞机的尾旋特性，首次利用一个满足动力相似的缩比模型在Ф5m尾旋风洞中进行研究试验，利用机载传感器所采集的模型运动参数来研判飞机模型的尾旋特性。目前，对于此类飞机模型尾旋运动中所承受的气动力矩研究还十分缺乏，以飞机模型尾旋试验结果为基础，采用飞机六自由度运动学方程来还原模型在尾旋运动中所承受的气动力矩系数，同时利用常规风洞测力试验结果来检验所还原的气动力矩系数的可靠性。进一步采用多元高次方程对模型尾旋运动进行了系统辨识研究，建立了能辨识飞机在尾旋运动条件下的气动力矩系数的数学模型，成功的辨识了重要的气动力系数的导数(Cmα,Cmδe,Cmq,Cnβ,Cnδr,Cnr,Clβ,Clδr,Clp)，与相关参考值比较显示其结果具有较高的可信度。

尾旋风洞；尾旋试验；系统辨识；气动力参数辨识

0 引言

大型民用飞机在运营时不允许进入失速状态，但在飞机的适航取证过程中失速试飞却是非常重要的一个环节。由于失速试飞是一项风险极大的飞行试验，试飞前需要对飞机在大迎角状态下的运动特性进行全面的、仔细的研究。飞机在大迎角过失速状态下的飞行状态包括：飞机大滚转、航向偏离、气动惯性旋转、尾旋等。尾旋是飞机的一种特殊的、危险的、非正常飞行状态，也是飞机的极限飞行状态之一。当飞机的飞行攻角大于失速攻角时，飞机会发生急剧的滚转和偏航运动，伴随着滚转和偏航飞机机头向下，并绕垂直轴以很小的半径沿着螺旋轨迹急速下降，这种现象被称为飞机尾旋。对于飞机设计师而言，设计一架飞机要使其具备良好的尾旋特性，即飞机本身具备较高的抗尾旋能力和良好的尾旋改出特性[1]。航空研究发展的今日，研究飞机尾旋的手段已是丰富多样，包括：六自由度运动方程的仿真计算、尾旋风洞试验、水平风洞模型自由飞试验、大气环境模型自由飞试验等[2-3]。尾旋风洞是一种具有垂直试验段的特种低速风洞，风扇垂直向上抽气，使得处于上升气流中的飞机模型所产生的浮力恰好平衡或近似平衡飞机模型的重力，来保证飞机模型能在试验段中心区域运动，所以尾旋风洞特别适合于用来研究飞行轨迹靠近或绕铅垂轴的飞行器运动，比如尾旋运动。

为了研究某常规布局(大展弦比、后掠翼、翼吊式发动机)大型民用飞机的尾旋特性与改出特性，需要在中国空气动力研究与发展中心的Ф5m尾旋风洞中进行相关试验研究，这是国内此类布局飞机首次在尾旋风洞中进行尾旋研究试验。在尾旋风洞中进行尾旋研究有两种方法：旋转天平试验和自由尾旋试验[2][4]。旋转天平试验的优点是能直接获得定量的气动力数据，缺点是不能从试验结果中直接判读出飞机的尾旋特性，而需要大量的后期数据处理才能获得确切的结论。自由尾旋试验的情况正好相反，在试验中所获得的运动参数能直接评判飞机的尾旋特性，能非常直接的判定模型的尾旋改出效果，但缺憾的是不能直接获得定量的气动力数据。从技术上讲这两种试验方法是可以相互印证相互补充的。基于成本、试验周期等因素的综合考虑，选择了利用自由尾旋试验技术进行飞机缩比模型的尾旋试验研究，通过飞机模型体内所装载的传感器来记录飞机模型在尾旋运动中的运动参数。在试验结果的基础上，将所记录的运动参数作为输入，利用六自由度运动学方程(6DOF EOM)运算来还原飞机模型在尾旋运动中作用在模型上的气动力矩系数。在获得了作用在飞机模型上总的气动力矩基础上，进一步利用飞机气动力参数辨识技术研判气动力矩系数的导数，其核心是建立气动力数学模型，气动力数学模型是建立作用于飞机的空气动力(CL，CD，Cm，CY，Cn，Cl)与飞机运动状态参数(V，Ω，α，β，H)和控制输入(δe，δr，δa，…)之间的解析关系式，建立数学模型是飞机气动特性分析所必不可少的，所获得的气动力导数既可以检验风洞试验结果，也可以检验工程估算结果。常用的气动力数学模型有三种：(1)代数模型；(2)积分方程模型；(3)微分方程模型。其中代数模型包括：线性气动力模型，多项式模型和样条函数模型[5-6]。当飞机在小攻角范围内和小扰动条件下运动时，采用线性气动力模型即可满足要求，且一般不需要交叉导数项。但当飞机处于诸如尾旋运动这样的大扰动运动时，线性模型就不再适用。多项式模型适用于非线性气动力数学模型，即气动静导数、舵面效率，动导数、旋转导数、交叉导数等取至二阶、三阶、四阶甚至更高阶的导数来满足飞机尾旋运动的高度非线性问题，具体的数学模型根据不同的飞机，不同的运动模态、不同的操纵方法，各有侧重，需要根据实际情况增加或删减项数与方次[7]。

1 飞机模型气动力矩系数的还原

在尾旋风洞进行自由尾旋试验过程中，通过在模型内部预装微型陀螺仪可以获得飞机模型的运动参数，如欧拉角(ψ，θ，φ)，体轴系下的三轴角速度(p，q，r)，通过相关公式换算可以求得气流坐标系与机体坐标系的夹角(α，β)[8]。但遗憾的是没有直接获得作用在飞机模型上的气动力数据。为了获得作用在模型上的气动力数据，就需要利用气动力数据还原技术，它是利用各种动态试验(尾旋风洞自由尾旋试验，风洞模型自由飞试验，大气模型自由飞试验，试飞试验)所获得的数据结果来还原气动力和力矩，采用的基本方程是飞机的六自由度运动学方程组。为了还原飞机尾旋运动中作用在飞机上的气动力，通常采用机体坐标系作为参考轴系，并设飞机有纵向对称平面zx，所以惯性积Iyz=Ixy=0。式(1)～(3)为无动力状态下围绕飞机机体坐标系下的三轴角加速度的表达式：

将式(1)～(3)进一步整理，即整理为滚转力矩、俯仰力矩和偏航力矩的表达式，如下：

体轴系下的角速度与欧拉角之间的关系如式(7)所示：

展开后为：

式(8)～(10)适用于描述飞机在初始尾旋阶段、尾旋发展阶段和尾旋改出阶段初期的飞行姿态和状态。根据有关资料介绍[9]，对于完全发展尾旋，在尾旋半径r尾旋=0和r尾旋≠0的条件下所获得的空气动力系数一般差别不大，因此对于研究完全发展尾旋，可以忽略尾旋半径的影响。此外，在完全发展尾旋中，飞机绕其质心的角速度是垂直的或近似垂直的，换句话说即飞机尾旋速度矢量与尾旋轴线重合或近似重合，基于这样一个前提，所以Ω=|dψ/dt|，dφ/dt=dθ/dt=0，则用欧拉角来表示的体轴系下的角速度公式可以简化为：

对角速度进行求导：

将角速度式(11)～(13)和角加速度式(14)～(16)带入气动力矩表达式(4)～(6)，并将其无量纲化：

在式(17)～(19)中，动压(q∝ρ，V)由试验中测量获得，惯量(Ix，Iy，Iz)和惯量积(Ixz)，以及参考面积(S)，平均气动弦长(c)与参考展长(b)为飞机固有参数，欧拉角(θ，φ)和尾旋旋转角速度(Ω)由试验中测量获得，欧拉角和尾旋旋转角速度随时间的导数(dθ/dt，dφ/dt，dΩ/dt)用数值微分法求解，这样就可以还原出飞机在尾旋中的气动力矩参数随时间变化的规律。若飞机模型在尾旋风洞试验中展现出稳定的、近似稳定(次稳定)的、或非常稳定的尾旋模态，则可以假定飞机体轴系下绕x，y，z三轴的角加速度和绕尾旋轴的角加速度近似为零，即dΩ/dt=dθ/dt=dφ/dt=0，则气动力矩系数式(17)～(19)可以整理成式(20)～(22)。

尾旋运动是惯性力矩与气动力矩在相互作用，由于产生尾旋的主要原因是飞机进入超临界攻角范围，而改出尾旋必须要减小攻角，所以首先的工作是研究能改变攻角的力矩—俯仰力矩，通过上面的俯仰力矩系数式(18)求得俯仰力矩系数随时间的变化曲线，并与简化式(21)的计算结果进行相互比较。自由尾旋试验中飞机构型为巡航构型，CG=25%MAC，模拟飞行高度5 000 m，舵面偏度δa=0°，δe=-30°，δr=30°，采用三中立法改出。图1 a)展示了利用六自由度运动方程和其简化方程所还原的俯仰力矩系数随时间变化的曲线比较，可以看出两者略有差异，但两者的宏观走势与各自的平均俯仰力矩系数基本一致，这说明自由尾旋试验中，绕飞机模型体轴下三轴的角加速度不为零，但量级较小。将所还原的俯仰力矩系数随攻角变化的曲线画在Cm～α图上，此外从飞机模型在Ф3.2m常规风洞进行的大攻角测力试验结果中提取在δe=0°/-30°条件下的纵向试验的Cm～α曲线，也展示在同一张图上。虽然两期试验的雷诺数有所差异，但雷诺数的影响主要集中在失速攻角附近，从失速攻角向大攻角发展，雷诺数的影响逐渐下降。此外方向舵偏转对纵向力矩的影响可以忽略。从图1 b)中可以看出当飞机模型处于完全发展稳定尾旋时，所还原的Cm随攻角在某一区域来回振荡，而δe=-30°条件下的静态测力试验所获得的Cm～α曲线穿过此一区域，所还原数据的平均攻角和平均俯仰力矩系数恰好就在测力试验Cm～α曲线的附近，几乎重合。这个结果说明了在大攻角条件下，动态试验的气动力矩还原结果与静态测力试验的结果具有良好的相关性。为了进一步证明此一结论，将起飞构型和着陆构型条件下的试验结果进行气动力矩的还原，再和静态测力试验结果分别比较，结果如图2所示。可以看出，起飞构型和着陆构型下，从自由尾旋试验结果中所还原的俯仰力矩系数与静态测力试验结果同样保持着良好的相关性。

2 飞机模型气动力矩的参数辨识

在还原出飞机模型在尾旋运动中所受总的气动力矩后，需要进一步辨识出构成此一总的气动力矩的每一部分气动力矩系数的导数。理论上总的气动力矩包含了三项：Mi=Mi静态+Mi振动+Mi旋转。以纵向力矩系数为例：Cm=Cm静态+Cm振动+Cm旋转，其中Cm静态=f(α，β，δe)，Cm振动=f(p，q，r，dα/dt，dβ/dt)，Cm旋转=f(Ω)。由于飞机尾旋运动是一种高度非线性的大扰动运动，所以需要采用多元高次多项式作为飞机尾旋时气动导数辨识的数学模型。首先进行俯仰力矩系数的参数辨识研究，所获得的多元高次多项式模型如式(23)所示。

关于Cm数学模型的相关系数R=0.990 33。利用所获得的气动力矩系数表达式重新计算飞机模型在尾旋运动中和尾旋改出过程中的Cm随时间变化的曲线，将所计算得到的曲线与由六自由度运动方程直接还原而得到的俯仰气动力矩随时间变化的曲线进行对比，对比结果如图3所示。从图中可以看出，所还原的Cm～t(s)曲线与六自由度运动方程的转换结果(观测值)基本吻合，波峰和波谷的量值基本接近，且没有明显的延迟现象。此外从飞机模型的大攻角静态测力试验结果中提取模型在尾旋中平均攻角所对应的俯仰力矩系数，展示在同一张图中，可以看出两条曲线在围绕大攻角测力试验的结果来回振荡。

利用同样的参数辨识方法获得能用来表达偏航力矩和滚转力矩变化的多元高次多项式数学模型，如式(24)～(25)所示。数学模型计算结果与观测值的比较如图4和图5所示。

经过对Cm，Cn和Cl的参数辨识，获得了飞机模型在尾旋运动条件下的有关气动力矩的静导数和部分主要的动导数(阻尼导数)，辨识的结果如表1所示，表中还列出了相关参考值(基于试验的计算结果与工程估算方法所计算的结果[10])和参数辨识结果进行对比，获得了比较良好的一致性。

表1中的对比结果显然是比较令人满意的，当然也需要承认尾旋风洞试验的一些特殊性：(1) 尾旋风洞试验的环境是恒定的，试验中风速与风速的方向没有发生任何的改变；(2) 大展弦比大型民用客机的尾旋模态比较稳定，攻角与侧滑角的振荡较小，机体轴系下三轴的角加速度变化相对战斗机均比较柔和，在实施改出动作前尾旋方向不发生变化。这些因素均对尾旋风洞试验结果的参数辨识研究提供了某种便利。

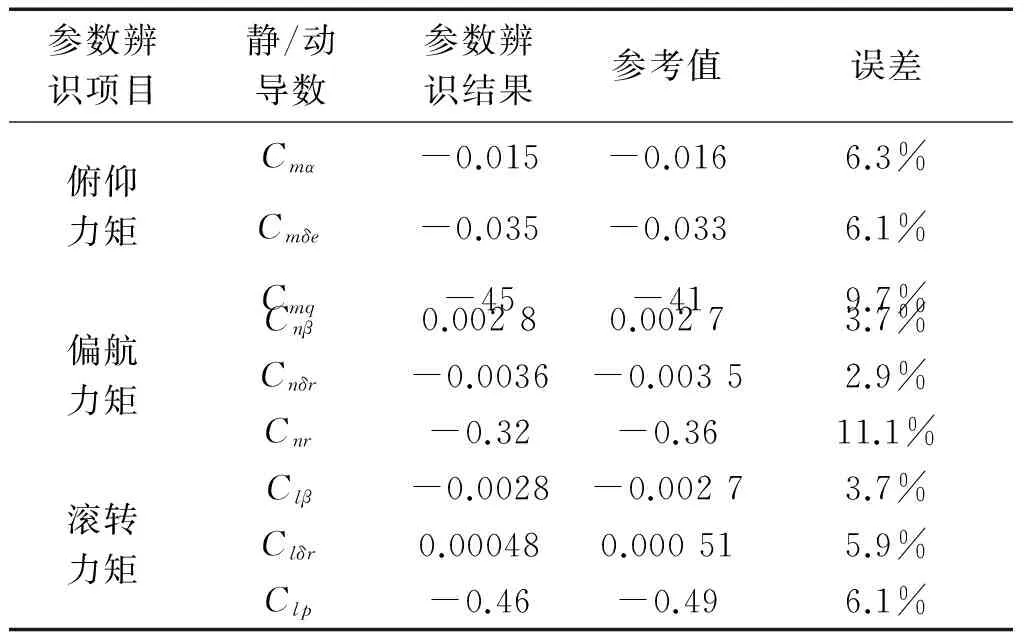
表1 参数辨识的结果比较

3 结论

本文基于某大型民用飞机缩比模型尾旋风洞试验的结果，利用六自由度运动方程计算获得了飞机模型自由尾旋运动状态下的气动力矩系数，并使用飞机模型常规风洞测力试验结果来验证动态试验结果的可靠性，弥补了尾旋风洞自由尾旋试验不能直接获得气动力矩数据的缺憾。在此基础上利用多元高次多项式进行了飞机模型的气动力矩参数辨识的研究，构建了相关气动力矩的数学模型，成功获得了静导数和部分动导数，和基于试验的计算结果与工程估算结果相对比，获得了比较良好的相关性。利用飞机气动力矩参数辨识结果所还原的气动力矩系数随时间变化的曲线与六自由度方程直接求取的气动力矩系数随时间变化的曲线基本吻合，相关性较好。

[1] 恽起麟.风洞试验[M].北京：国防工业出版社，2000.

[2] 李永，陈洪.研究尾旋的风洞试验技术[M]. 北京：国防工业出版社 2002.

[3] MURCH A, FOSTER J. Recent NASA Research on Aerodynamics Modeling of Post-Stall and Spin Dynamics of Large Transport Airplanes[C]// 45th AIAA Aerospace Science Meeting, Jan 2007 Reno Nevada.

[4] Rotary-Balance Testing for Aircraft Dynamics[R]. AGARD Advisory Report No.265

[5] TISCHLER M, REMPLE R. Aircraft and rotorcraft system identification: engineering methods with flight-test examples [M]. AIAA education series Dec. 2012

[6] KLEIN V, MORELLI E. Aircraft system identification: theory and practice[M]. AIAA 2006

[7] 黄灵恩，潘怡.从模型尾旋试飞数据中辨识气动力的初步探索[C]// 中国2000年飞行力学与飞行试验学术年会论文集，2000： 283.

[8] FREMAUX C. Spin-Tunnel Investigation of a 1/28-Scale Model of the NASA F-18 High Alpha Research Vehicle (HARV) With and Without Vertical Tails[R]. NASA Contractor Report 201687

[9] M Г 科契克.飞机螺旋动力学[M].中国人民解放军空军司令部译，1978.6

[10] 张锡金主编.飞机设计手册第6册：气动设计[M]. 北京：航空工业出版社，2002.

Systems Identification Research of a Large Spin Motion for Civil Aircraft

(Shanghai Aircraft Design and Research Institute, Shanghai 201210, China)

A dynamic similarity scaled aircraft model was tested in spin tunnel to investigate spin characteristics of a large civil aircraft in first time. The spin characteristic of aircraft model was investigated based on kinematic parameters which was recorded by sensors. The research on aerodynamic moment which acts on the aircraft model in spin motion is still very absent. Base on results of the large civil aircraft model free-spin test, aerodynamic moments were calculated by six degree freedom equation of motion, reliability of calculated results were validated by the comparison with results of force measurement of aircraft model in normal wind tunnel in this paper. Finally, system identification research of aircraft model spin motion was carried out, multivariate polynomial equation was used. The mathematical model which can be used to identify the moment coefficients was created, several important aerodynamic derivative was identified, such asCmα,Cmδe,Cmq,Cnβ,Cnδr,Cnr,Clβ,Clδr,Clp. These derivatives were validated by the reference value.

spin tunnel; spin test ; system identification; aerodynamic parameter identification

V328

A

10.19416/j.cnki.1674-9804.2017.04.011

国家中长期科学与技术发展规划纲要——大型飞机研制专项基金

颜巍男，博士，工程师。主要研究方向：飞行器大迎角空气动力学研究和飞行器偏离尾旋研究；E-mail:yanwei2@comac.cc

黄灵恩男，本科，研究员。主要研究方向：飞行器大迎角空气动力学研究和飞行器偏离尾旋研究

黎先平男，博士，研究员。主要研究方向：飞行器大迎角空气动力学研究和飞行器偏离尾旋研究；E-mail:lixianping@comac.cc