例说充分条件、必要条件常见判断法

夏鸿鑫

充分条件、必要条件的判断是“常用逻辑用语”中的重点也是难点，学生对此类问题以猜、估为主，因而常常出错，对此，本文用一例谈谈充分条件、必要条件六种常见判断方法.

例指出下列命题中，p是q的什么条件（填“充分必要条件”“必要不充分条件”“充分不必要条件”或“既不充分也不必要条件”之一）.

（1）p：a+b+c=0，q：1是方程ax2+bx+c=0的一个根.

（2）p：x≠2或y≠3，q：x+y≠5.

（3）p：m+3<0，q：方程x2-x-m=0没有实数根.

（4）p是r的充要条件，r是s的必要不充分条件，s是q的必要条件.

（5）p：|x|<1，|y|<1，q：|x+y|+|x-y|<2.

（6）p：α，β是第一象限角，α>β，q：α，β是第一象限角，tanα>tanβ.

解（1）定义法：

若a+b+c=0，有a×12+b×1+c=0，则1是方程ax2+bx+c=0的一根，即pq；

反之，若1是方程ax2+bx+c=0的一根，有a×12+b×1+c=0，则a+b+c=0，即qp.

故p是q的充分必要条件.

评注：判断p是q的什么条件，通常是根据充分、必要条件的定义分析判断，由p成立时，能否推出q成立，得到是否具有充分性；反过来，q成立时，能否推出p成立，得到是否具有必要性.

（2）等价命题法：

瘙 綈 p：x=2且y=3，

瘙 綈 q：x+y=5，显然有

瘙 綈 p

瘙 綈 q且

瘙 綈 q

瘙 綈 p，即qp且pq，故p是q的必要不充分条件.

评注：当含有命题否定形式时，可利用互为逆否命题同真同假进行转化后加以判断.

（3）集合法：

p的真值集合为A={|m<-3}，由方程x2-x-m=0没有实数根得Δ=（-1）2-4（-m）<0，即m<-14，则q的真值集合为B=mm<-14，显然AB，故p是q的充分不必要条件.

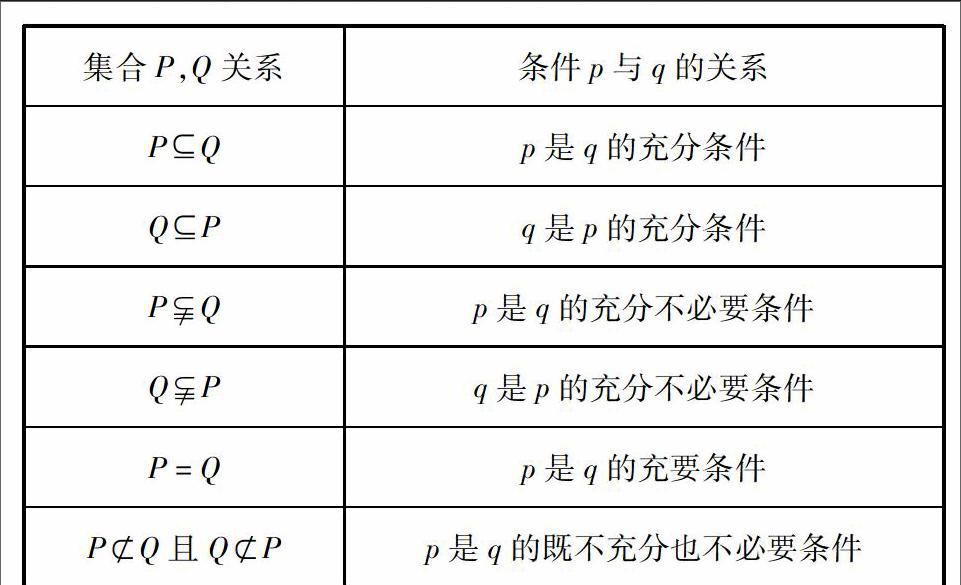
评注：满足条件p的元素构成集合P，即P={x|p（x）}，满足条件q的元素构成Q，即Q={x|q（x）}.条件p与q的关系也可根据集合P，Q之间的关系加以判断.

集合P，Q关系条件p与q的关系

PQp是q的充分条件

QPq是p的充分条件

PQp是q的充分不必要条件

QPq是p的充分不必要条件

P=Qp是q的充要条件

PQ且QPp是q的既不充分也不必要条件

（4）传递法：

由题意，pr，sr，但rs，qs，

从而有qsrp，但pq，

所以p是q的必要不充分条件.

评注：由充分条件、必要条件概念知，如果pq，qr，rs，st，则pt，也就是p是t的充分条件，这一点类似于等量（不等量）傳递性.

（5）图形法：

由题意，|x|<1，|y|<1，是中心在原点边长为2的正方形内部区域（不包括边界）.

|x+y|+|x-y|<2，在第一象限内：

① 当x>0，y>0，x>y，得x<1；

② 当x>0，y>0，x

图1

图2

然而，根据对称性得到整个区域是中心在原点，边长为2的正方形内部区域（不包括边界），两个区域完全一致，所以p是q的充要条件.

评注：命题p，q所表示的元素是点集时，可考虑作出它们对应的区域（图形），再比较区域（图形）之间的包含关系.

（6）特取法：

如，α=361°，β=89°，α>β/tanα>tanβ，

反过来，α=89°，β=361°，tanα>tanβ/α>β，

即p/q，且q/p，故p是q的既不充分也不必要条件.

评注：对于不能推断出的命题，可以举出反例（哪怕只有一个）即可.

巩固指出下列命题中p是q的什么条件（填“充分必要条件”“充分不必要条件”“必要不充分条件”“既不充分也不必要条件”之一）.

（1）设实数a>1，b>1，p：aa-b.

（2）p：a≠β，q：tanα≠tanβ.

（3）p：函数y=2x+m-1（m∈R）有零点，

q：函数y=logmx（m>0且m≠1）在（0，+

SymboleB@ ）上为减函数.

（4）在△ABC中，a，b，c是A，B，C的对边，p：A>B，r：a>b，q：sinA>sinB.

（5）设a>0，b>0，p：a2+b2<1，q：ab+1>a+b.

（6）设x∈R，p：1

答案（1）充分必要条件；

（2）必要不充分条件；

（3）必要不充分条件；

（4）充分必要条件；

（5）充分不必要条件；

（6）既不充分也不必要条件.