无线传感器网络中基于“k−覆盖问题”的多项式时间算法

2018-01-08王骐肖正安王怀兴

电信科学 2017年12期

关键词：边界线分界线切点

王骐，肖正安，王怀兴

无线传感器网络中基于“−覆盖问题”的多项式时间算法

王骐，肖正安，王怀兴

（湖北第二师范学院物理与机电工程学院，湖北武汉 430205）

无线传感器网络；−覆盖问题；扩展圆盘；相邻分界线；多项式时间算法

1 引言

2 基于UDG的几何图形

2.1 问题的描述

图1 −违反值和−支持值示意

2.2 圆盘的扩展

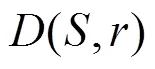
图2 大于的“2−违反”路径

同理可得定理2。

3 解决方案——多项式时间算法

3.1 子区域及其分界线

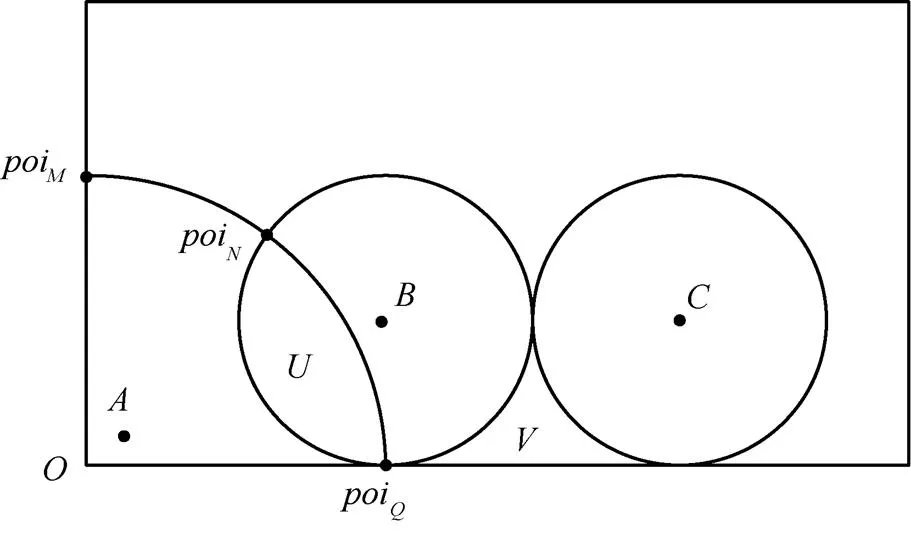
图3 子区域及其分界线

由于这段弧是由两个相邻子区域相交的公共部分，分属的两个子区域的覆盖度可能不相同，所以根据定义5来计算这段弧的覆盖度就会产生矛盾[11]。为此特做以下定义。

图4 内弧和外弧

定义7 （相邻分界线）如果两段分界线（内弧、外弧或边界线）具有公共点，那么称这两段分界线为相邻分界线。

根据定义7，由于同一段弧的内弧和外弧具有无限多个共同点，因此它们互为相邻弧。当且仅当两段分界线具有相同交点或切点时，它们互为相邻分界线，如图3所示。由于子区域可看成是由若干相邻分界线形成的，因此，这些分界线具有和子区域相同的覆盖度。

Procedure:/*计算所有的分界线，并且判定两段分界线是否为相邻分界线

input: 传感器节点集{1,2,…, s}，圆半径

output: 分界线集{1,2,…, bor}

for1 to

计算disk和所有其他圆或边界线的交点或切点

for 圆周线上的每对相邻交点或切点

定义分界线bor

划分bor为内弧和外弧

for 平面边界线上的每对相邻交点或切点

定义分界线bor

/*计算每段分界线的覆盖度

for 每段分界线bor

switch（分界线类型）

casebor为边界线的一部分

选取点poi∈bor

计算点poi的范围内传感器节点数量

casebor为一段外弧

选取点poi∈bor

计算点poi的范围内传感器节点数量，不包括poi所属圆的中心节点

casebor为一段内弧

选取点poi∈bor

计算点poi的范围内传感器节点数量，包括poi所属圆的中心节点

/*判定两段分界线是否互为相邻分界线

set 所有分界线为非相邻分界线

for 每个交点或切点poi

ifpoi为bor和bor的端点

setbor和bor为相邻分界线

end

3.2 最差k−覆盖问题

input: 边界线集合{1,2,…,},∈,∈

output: 布尔变量结果值

if()≥或() ≥

= 0

return

取消所有分界线的标记

标记/*起始于

list=

tree=

while（非空）

从链表头选取分界线

从链表删除分界线

for相邻的每段分界线

if()

标记

在树上将作为的孩子

在链表尾增加

if被标记

= 1

return

else

= 0

return

end

set/*设定搜索空间的上限值

set/*设定搜索空间的下限值

set/*设定迭代次数

for= 1 to

= (+)2

{1,2,…,}=() /*调用函数(,)计算所有的分界线

if= 1

else

end

上限值和下限值可根据平面维度以及传感器节点的密度来设定。每次迭代将使搜索空间减半，例如，如果搜索空间（||）的值为1 000，经过10次迭代可得到结果，且误差小于1。一般情况下，10～20次迭代可足以确保结果的准确性[15]。

3.3 最佳k−覆盖问题

4 仿真结果

图5 k−违反的最大值

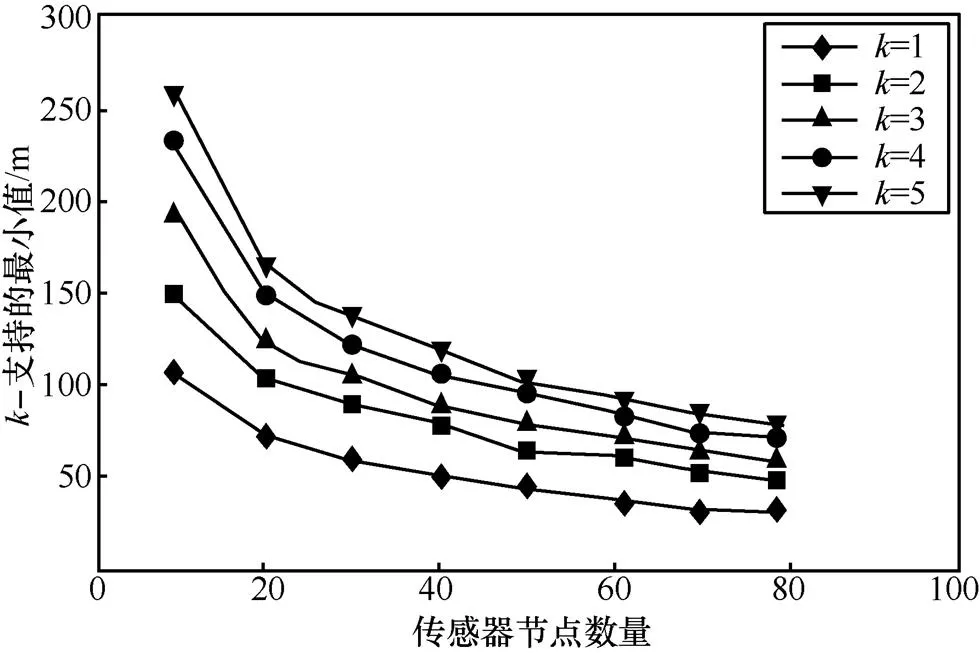
图6 k−支持的最小值

对比图5和图6，可得到以下结论。

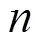
• 当传感器节点数量相同时，−支持的最小值要远大于−违反的最大值。可以证明，任何情况下，−支持的最小值均不会小于−违反的最大值。

5 结束语

本文分别阐述了最差和最佳−覆盖问题，并基于扩展圆盘的几何图形提出了一系列的定义和定理，将−覆盖问题转化成了寻找相邻分界线的问题，提出了解决此问题的多项式时间算法。

[1] MEGERIAN S, KOUSHANFAR F, POTKONJAK M, et al. Worst and best-case coverage in sensor networks[J]. IEEE Transaction on Mobile Computing, 2005, 4(1):84-92.

[2] 杨海雳, 赵静. 基于Voronoi图的无线传感器网络覆盖算法研究[J]. 信息通信, 2015(7):28-31.

YANG H L, ZHAO J. Research of coverage algorithm with Voronoi diagram for wireless sensor network [J]. Information & Communications, 2015(7):28-31.

[3] 王成, 樊建席, 王仁喜, 等. 基于Voronoi图的无线传感器网络K覆盖算法[J]. 计算机工程, 2012, 38(4):84-87.

WANG C, FAN J X, WANG R X, et al. K coverage algorithm in wireless sensor network based on Voronoi diagram[J]. Computer Engineering, 2012, 38(4):84-87.

[4] 丁旭, 吴晓蓓, 黄成. 基于改进粒子群算法和特征点集的无线传感器网络覆盖问题研究[J]. 电子学报, 2016, 44(4): 967-973.

DING X, WU X P, HUANG C. Area coverage problem based on improved PSO algorithm and feature point set in wireless sensor networks[J]. Acta Electronica Sinica, 2016, 44(4) : 967-973.

[5] 孙泽宇, 伍卫国, 王换招, 等. 无线传感器网络基于参数可调增强型覆盖控制算法[J]. 电子学报, 2015, 43 (3):466-474.

SUN Z Y, WU W G, WANG H Z, et al. An enhanced coverage control algorithm for wireless sensor networks based on adjustable parameters[J]. Acta Electronica Sinica, 2015, 43 (3): 466-474.

[6] 刘志强, 沈廼桐, 毛强, 等. 无线传感器网络动态覆盖的CVT算法[J]. 传感器与微系统, 2015(6):115-118.

LIU Z Q, SHEN N T, MAO Q, et al. A dynamic coverage algorithm for wireless sensor networks based on CVT[J]. Transducer and Microsystem Technologies, 2015(6):115-118.

[7] 高洁, 吴延红, 白建侠, 等. 无线传感器网络最小覆盖能量优化算法[J]. 传感技术学报, 2016, 29(9):1435-1440.

GAO J, WU Y H, BAI J X, et al. The minimum coverage energy optimization algorithms in wireless sensor network[J]. Chinese Journal of Sensors And Actuators, 2016, 29(9):1435-1440.

[8] LIU X Y, WU K L, ZHU Y, et al. Mobility increases the surface coverage of distributed sensor networks[J]. Computer Networks the International Journal of Computer & Telecommunications Networking, 2013, 57(11):2348-2363.

[9] TAN L, CHENG Y C, YANG M H, et al. Priority coverage algorithm and performance simulation for node deployment in directional sensor networks[J]. Sensor Letters, 2014, 12(2): 275-280.

[10] 鲁晓波, 阮福, 王立中. 无线传感器网络覆盖优化策略[J]. 内蒙古师大学报(自然汉文版), 2016, 45(4):480-483.

LU X B, RUAN F, WANG L Z. Coverage optimization strategy of wireless sensor networks based on improved artificial fish swarm algorithm[J]. Journal of Inner Mongolia Normal University (Natural Science Edition), 2016, 45(4):480-483.

[11] 王兴伟, 蔡凌, 黄敏, 等. 基于空间镶嵌的三维无线传感器网络覆盖机制[J]. 小型微型计算机系统, 2014, 35(3): 433-436.

WANG X W, CAI L, HUANG M, et al. Spatial tessellation basedcoverage scheme for 3D wireless sensor network[J]. Journal of Chinese Computer Systems, 2014, 35(3):433-436.

[12] MINI S, UDGATA S K, SABAT S L. Sensor deployment and scheduling for target coverage problem in wireless sensor networks[J]. IEEE Sensors Journal, 2014, 14(3):636-644.

[13] MAHBOUBI H, MOEZZI K, AGHDAM A G, et al. Distributed deployment algorithms for improved coverage in a network of wireless mobile sensors[J]. IEEE Transactions on Industrial Informatics, 2013, 10(1):163-174.

[14] ZHANG Y, SUN X, WANG B. Efficient algorithm for-barrier coverage based on integer linear programming[J]. China Communications, 2016, 13(7):16-23.

[15] BAN D S, WEN J, JIANG J, et al. Constructing-barrier coverage in mobile wireless sensor networks[J]. Journal of Software, 2011, 22(9):2089-2103.

Polynomial time algorithm for solving-coverageproblem in wireless sensor networks

WANG Qi, XIAO Zheng’an, WANG Huaixing

School of Physics and Electromechanical Engineering, Hubei University of Education, Wuhan 430205, China

How to solve the-coverage problem, which was divided into worst-case and best-case, inside the two-dimensional target area in wireless sensor networks was explored, and a polynomial time algorithm for solving this problem was put forward. In this algorithm, a series of definitions and theorems were proposed based on the geometric graph of growing disks, and the-coverage problem was transformed into one of finding a series of adjacent borders. The simulation results show that the algorithm could compute the optimal-breach path and-support path in polynomial time, so as to avoid or select the network coverage reasonably.

wireless sensor network,-coverage problem, growing disk, adjacent border, polynomial time algorithm

TN918.91

10.11959/j.issn.1000−0801.2017287

2017−07−20；

2017−09−30

湖北省高等学校优秀中青年科技创新团队计划项目（No.T201417）

Hubei Provincial Department of Education Research Program (No.T201417)

王骐（1970−），男，博士，湖北第二师范学院物理与机电工程学院副教授，主要研究方向为无线传感器网络安全、嵌入式系统应用。